絵算からテキスト、そして可換図式化もやってみた（当然疲れた）

「絵算のテキスト化を完全にやってみた（超・疲れた）」において、絵算の計算過程を、行列レイアウトの等式的推論としてテキストに写し取ってみました。これは、値を変えずに項を変形していく過程で、通常の等式変形（等式論理系における証明）そのものです。

ところで圏論では、可換図式が多用されます。可換図式が、圏論で一番ポピュラーな記述・計算デバイスなのです。この記事では、絵算やそのテキスト表現を可換図式にしてみます。また、この機会に可換図式に関する説明もします。

内容：

結合律の可換図式
この可換図式はどうやって作ったか
可換図式とは何なのか
可換図式と他の表現方法
おわりに

結合律の可換図式

以下の記事達で、強モナドから作られたモノイドの結合律を題材にしました。

もとの定理（結合律 (m $\otimes$ N);m = α_N,N,N;(N $\otimes$ m);m）の内容はあんまり気にしなくていいです。同じ定理の記述と証明を、いろんな手法でやってみようというノリです。

結合律の絵による証明とテキスト（項と等式）による証明は既に述べたので、可換図式〈commutative diagram〉による証明を挙げましょう。以下の図がソレです。GraphVizで描いたので、雰囲気〈フレーバー〉が普通の可換図式とは違います*1が、内容的には紛れもなく可換図式です。

画像へのリンク

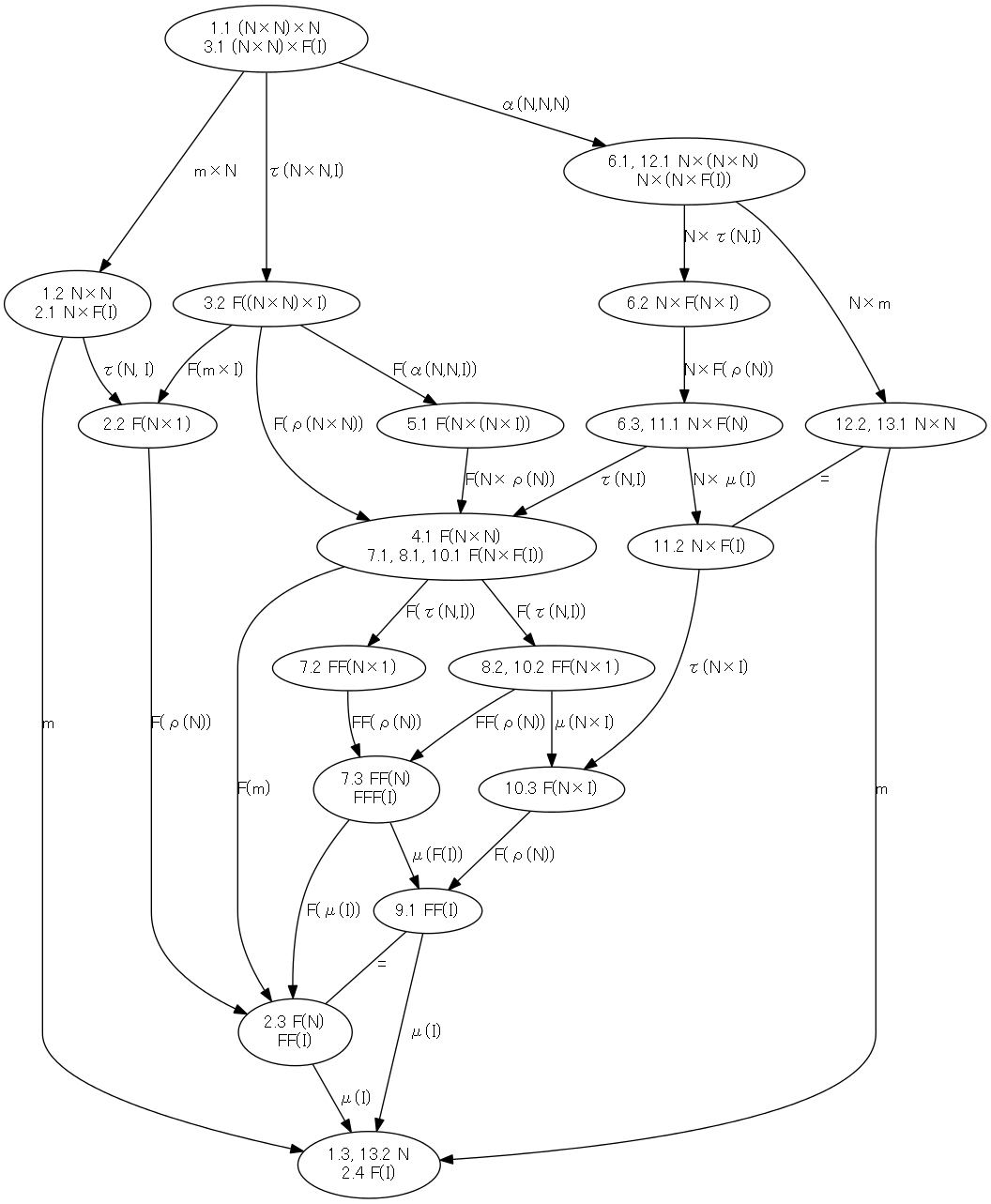
この可換図式が結合律の証明になっていることや、他の証明手法との関連などについて説明していきます。

この可換図式はどうやって作ったか

先の可換図式は、「絵算のテキスト化を完全にやってみた（超・疲れた）」で書いたテキスト表現をもとにして作りました。テキスト項の番号が1から13（trm1からtrm13）まであるので、そのなかに出現する目ぼしい対象に枝番（例えば、3.1, 3.2）を付けます。その対象を可換図式のノードにして、射を矢印として描きます。異なる項に出現する同一対象は同一ノードにマップされることもあります。

手描きするにしろ、TeXパッケージを使うにしろ、可換図式のレイアウトを調整するのは苦痛なので、自動レイアウトを行うソフトウェアであるGraphVizを使いました。DOT言語によるデータを作れば、あとはGraphVizがやってくれます。

DOT言語のソースは以下のとおりです。オプション（属性）はすべてデフォルトで、見た目の調整は何もしてません。モノイド積を表すテンソル積記号' $\otimes$ 'は入力が面倒なので'×'で代用しています。自然変換の下付き添字（τ_N,Iの'N,I'など）は丸括弧の引数形式（例：τ(N,I)）にしています -- 丸括弧引数でも何の不都合もないし、むしろ便利なので僕はよく使います。

// -*- coding: utf-8 -*-
// This is m2m-assoc.gv

digraph Assoc {


/* 1 */
trm1_1 [label="1.1 (N×N)×N\n3.1 (N×N)×F(I)"];
trm1_2 [label="1.2 N×N\n2.1 N×F(I)"];
trm1_3 [label="1.3, 13.2 N\n2.4 F(I)"];
  trm1_1 -> trm1_2 [label="m×N"];
  trm1_2 -> trm1_3 [label="m"];

/* 2 */
    trm1_2 -> trm2_2 [label="τ(N, I)"];
// trm2_1 = trm1_2
trm2_2 [label="2.2 F(N×1)"];
trm2_3 [label="2.3 F(N)\nFF(I)"];
  trm2_2 -> trm2_3 [label="F(ρ(N))"];
    trm2_3 -> trm1_3 [label="μ(I)"];

/* 3 */
    trm1_1 -> trm3_2 [label="τ(N×N,I)"];
// trm3_1 = trm1_1
trm3_2 [label="3.2 F((N×N)×I)"];
    trm3_2 -> trm2_2 [label="F(m×I)"];

/* 4 */
    trm3_2 -> trm4_1 [label="F(ρ(N×N))"];
trm4_1 [label="4.1 F(N×N)\n7.1, 8.1, 10.1 F(N×F(I))"];
    trm4_1 -> trm2_3 [label="F(m)"];

/* 5 */
    trm3_2 -> trm5_1 [label="F(α(N,N,I))"];
trm5_1 [label="5.1 F(N×(N×I))"];
    trm5_1 -> trm4_1 [label="F(N×ρ(N))"];

/* 6 */
    trm1_1 -> trm6_1 [label="α(N,N,N)"];
trm6_1 [label="6.1, 12.1 N×(N×N)\nN×(N×F(I))"];
trm6_2 [label="6.2 N×F(N×I)"];
trm6_3 [label="6.3, 11.1 N×F(N)"];
  trm6_1 -> trm6_2 [label="N×τ(N,I)"];
  trm6_2 -> trm6_3 [label="N×F(ρ(N))"];
    trm6_3 -> trm4_1 [label="τ(N,I)"];

/* 7 */
    trm4_1 -> trm7_2 [label="F(τ(N,I))"];
// trm7_1 = trm4_1
trm7_2 [label="7.2 FF(N×1)"];
trm7_3 [label="7.3 FF(N)\nFFF(I)"];
  trm7_2 -> trm7_3 [label="FF(ρ(N))"];
    trm7_3 -> trm2_3 [label="F(μ(I))"];

/* 8 */
// trm8_1 = trm4_1
    trm4_1 -> trm8_2 [label="F(τ(N,I))"];
trm8_2 [label="8.2, 10.2 FF(N×1)"];
    trm8_2 -> trm7_3 [label="FF(ρ(N))"];

/* 9 */
    trm7_3 -> trm9_1 [label="μ(F(I))"];
trm9_1  [label="9.1 FF(I)"];
    trm9_1 -> trm1_3 [label="μ(I)"];
    trm9_1 -> trm2_3 [label="=", arrowhead="none"];

/* 10 */
// trm10_1 = trm4_1
// trm10_2 = trm8_2
trm10_3 [label="10.3 F(N×I)"];
  trm8_2 -> trm10_3 [label="μ(N×I)"];
    trm10_3 -> trm9_1 [label="F(ρ(N))"];

/* 11 */
    trm6_3 -> trm11_2 [label="N×μ(I)"];
// trm11_1 = trm6_3
trm11_2 [label="11.2 N×F(I)"];
// trm11_3 = trm10_3
    trm11_2 -> trm10_3 [label="τ(N×I)"];

/* 12 */
    trm6_1 -> trm12_2  [label="N×m"];
// trm12_1 = trm6_1
trm12_2  [label="12.2, 13.1 N×N"];
    trm12_2 -> trm11_2  [label="=", arrowhead="none"];

/* 13 */
// trm13_1 = trm12_2
// trm13_2 = trm1_3
    trm12_2 -> trm1_3 [label="m"];

}

このファイルm2m-assoc.gvをレンダリングするには、次のようなコマンドラインを使います。

dot -Nfontname="ノード用フォント名" -Efontname="辺用フォント名" -Tpng m2m-assoc.gv -odiagram.png

ここで、フォント名指定は環境に依存するので、適当なフォント名で置き換えてください。

可換図式とは何なのか

圏論における可換図式とは、ノードが対象、有向辺が射を表す有向グラフです。「可換」と呼ばれるのは、2つのノード間を結ぶどんなパス〈道 | 経路〉も同じ射を表すと約束されているからです。図式（有向グラフ）内の多角形領域が、射のあいだの等式になっているのです。

可換図式	圏の概念
ノード	対象
辺	基本的な射
パス	結合により得られた射
多角形領域	射の同一性、等式

我々の例である結合律の可換図式で言えば、1.1（または3.1）とラベルされた一番上のノードから、1.3（または2.4, 13.2）とラベルされた一番下のノードに至るすべてのパスは等しい射です。特に、左側外周を通るパス (m×N);m と、右側外周を通るパス α(N,N,N);(N×m);m は等しいので、この図式には次の等式が含まれます。

(m×N);m = α(N,N,N);(N×m);m

より普通の記法だと：

(m $\otimes$ N);m = α_N,N,N;(N $\otimes$ m);m

可換図式に含まれる多角形領域が全部で12個あります。それぞれの多角形領域が射の等式を表しています。左外周パスから、多角形領域を横断しながら、パスを右へ右へとズラしていくと、最終的に右外周パスに到達します。このように、パスをズラしていく過程が証明です。

証明の最初の2つのステップだけ書いてみると。

四角形1.2, 1.3, 2.2, 2.3 （下の一番目の図）
- 最初のパス： (m×N);m （左外周のパス）
- 等式： m = τ(N,I);F(ρ(N));μ(I)
- 結果のパス： (m×N);τ(N,I);F(ρ(N));μ(I)
四角形1.1, 1.2, 2.2, 3.2 （下のニ番目の図）
- 最初のパス： (m×N);τ(N,I);F(ρ(N));μ(I)
- 等式： (m×N);τ(N,I) = τ(N×N,I);F(m×I)
- 結果のパス： τ(N×N,I);F(m×I);F(ρ(N));μ(I)

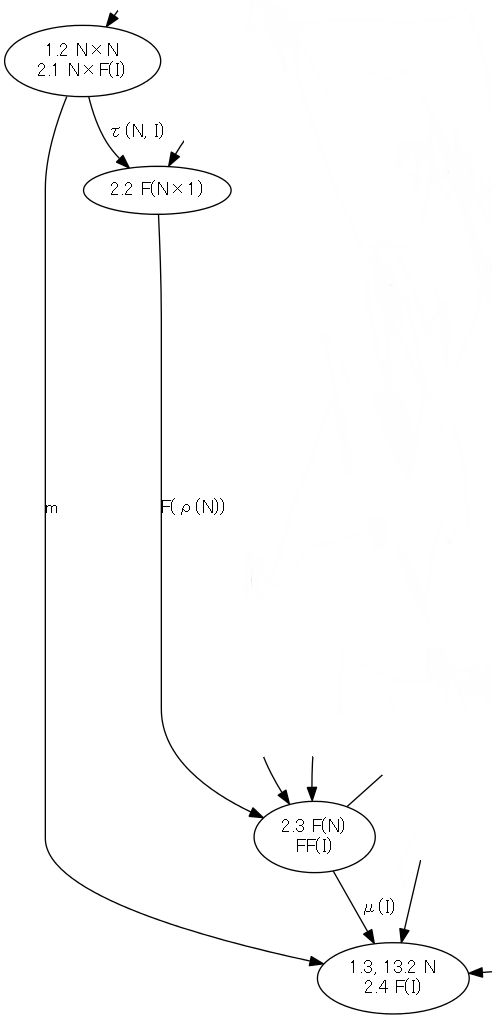
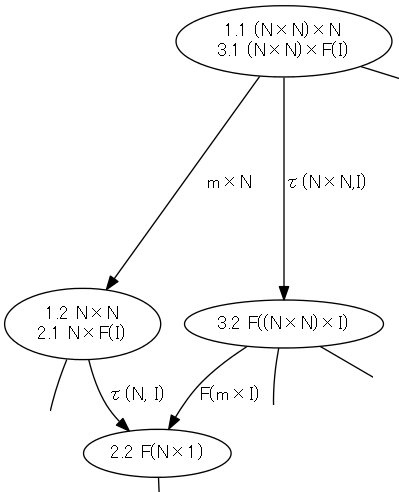
可換図式では、何も書いてない空白の多角形領域にこそ意味があるのです。この領域に、使った法則とか説明とかを書ければいいのですが、組版やレンダリングの都合でそういうことは出来ません。対話的グラフィックスを使って、領域をクリックすると説明がポッポアップするとか、解説ページへのハイパーリンクを辿るとか出来るソフトウェアがあるといいのですが。

可換図式は、単一の等式や、組織化された複数の等式群を表現するグラフィックスです。意味的には等式、または等式の連鎖と同じなので、定理の記述や証明に可換図式が利用されるのです。

可換図式と他の表現方法

可換図式と他の表現方法（等式的推論、絵算、アニメーション）との対応は次のようにまとめられます。

可換図式	等式的推論	絵算	アニメーション
パス	項	絵	フレーム（スチル）
多角形領域	等式	絵の変形	フレーム遷移
可換図式全体	等式的証明	絵証明	ムービー

いずれも一長一短で、これがベストという表現手段はないです。

そもそも、圏論で使う記述・証明デバイスに関しては、これといったテクノロジーがなく、旧態依然たる紙の数式組版（の電子版）だけしか利用できません。とても不幸な事態だと思います。

望ましいのはアニメーションによる記述・表現でしょう。何十年か後の人々は、VR／AR技術により体感する記述・証明デバイスにより、計算や証明をしているでしょう（「「コミュニケーションの多次元化」という革命に立ち会っているのだと思う」参照）。そのときが出来るだけ早く来るといいのですが。何十年後まで生きてられねーからな。