自然数の大小順序だけでも、まだネタはありますし、もう少し練習問題があったほうがいい気もします。全称記号∀に関する説明が不足してるし、∀と∃の関係も述べていません。が、長くなるので今回はこのくらいにしておきます。
ということで、そのまま続きを書きます。前回の記事を読んでいることを前提にするので、予備知識や記法の約束の繰り返しはしません。
内容:
全称記号と存在記号に関する推論規則
全称記号∀を含む命題と存在記号∃を含む命題に対する推論規則は、それぞれに導入規則〈introduction rule〉と除去規則〈elimination rule〉があり、合計で4つの規則となります。論理の教科書によくあるスタイル(望ましいスタイルとは思ってない)で規則を書くと:
P ∀x.P
------------[∀導入] ----------[∀除去]
∀x.P[a:=x] P[x:=t]
P ∃x.P
------------[∃導入] ----------[∃除去]
∃x.P[t:←x] P[x:=a]
規則の記述のなかで使っている記号を説明します。
- Pは命題です。正確に言えば、述語論理の論理式を表すメタ変数がPです。
- xとaは変数(を表すメタ変数)ですが、xは束縛変数で、aは自由変数とします。実際に使う変数を'x', 'a'って決めてるわけじゃないですよ。メタ変数xが表す実際の変数がaのときもあります。
- tは項(を表すメタ変数)です。定数、変数、関数(の記号)の組み合わせが項です。
ブラケット〈角括弧〉は置換を表します。4つのルールで、置換の仕方は微妙に違います。
- ∀導入 ∀x.P[a:=x] : 自由変数の束縛変数化 : Pに含まれていた自由変数aを束縛変数xに置き換える。
- ∀除去 P[x:=t] : 束縛変数の具体化 : Pに含まれていた束縛変数xを項tで置き換える。
- ∃導入 ∃x.P[t:←x] : 具体項の束縛変数化 : Pに含まれていた項tを束縛変数xで置き換える。これだけ特殊で(なので違う記号を使っている)、具体物を表す項に対して置き換えを行う。tが複数箇所に出現しても、出現箇所を特定して置き換える。つまり、置換しないままのtが残ってもかまわない。
- ∃除去 P[x:=a] : 束縛変数の条件付き自由変数化 : Pに含まれていた束縛変数xを自由変数aで置き換える。ただし、自由変数aには条件が付く(その意味で「自由」という呼び方は違和感があるかも)。
この節冒頭のスタイルで推論規則を書くのは望ましくない、と言ったのは、前回に述べたボックスの構造が全く含まれていないからです。∃除去で使うボックスが前回の主たる話題でした。∀導入にもボックスが付きます。ボックスなしでは実用的なテンプレートとしては不十分なので、推論バー(横棒)しか書かないスタイルは実用性に乏しいと思うのです。
全称命題を準備するボックスを使ってみよう: 最小元の存在
∀x∈N.(a ≦ x) という論理式は、「aがNの最小元である」という意味です。「Nに最小元が存在する」なら、次の論理式になります。
- ∃a∈N.∀x∈N.(a ≦ x)
大小関係≦の定義は次のようであり、この定義は我々の暗黙の前提Γに入っているのでした。
- ∀x, y∈N(x ≦ y ⇔ ∃z∈N.(x + z = y)) ---(大小順序の定義)
この定義を用いると、a ≦ x は ∃z∈N.(a + z = x) のことなので、「Nに最小元が存在する」は次のことです。
- ∃a∈N.∀x∈N.∃z∈N.(a + z = x)
これをターゲットとする証明要求は:
- Γ |-? ∃a∈N.∀x∈N.∃z∈N.(a + z = x)
我々は経験上、自然数の最小元といえば0だと知っています。実際、ターゲットを示す証明の出発点は、∀a∈N.(a + 0 = a) という命題で、これはΓに入っています。先に当該命題の証明を示して、後に説明を続けます。なお、ドルマーク('$')が付いたラベルは、既に前提Γに入っている命題の引用を示します。
証明要求: Γ |-?
∃a∈N.∀x∈N.∃z∈N.(a + z = x)
BEGIN ∀導入
x∈N
∀a∈N.(a + 0 = a) ---$(ゼロの中立性)
--[∀除去 a:=x]
x + 0 = x
// 交換律より
0 + x = x
--[∃導入 等式左辺のx:←z]
∃z∈N.(0 + z = x)
END
●∀x∈N.∃z∈N.(0 + z = x)
--[∃導入 0:←a]
∃a∈N.∀x∈N.∃z∈N.(a + z = x)
前回既に、∃除去ボックスを出したので、∀導入ボックスにも違和感はないでしょう。∀導入ボックスを絵で描けば次のようです。
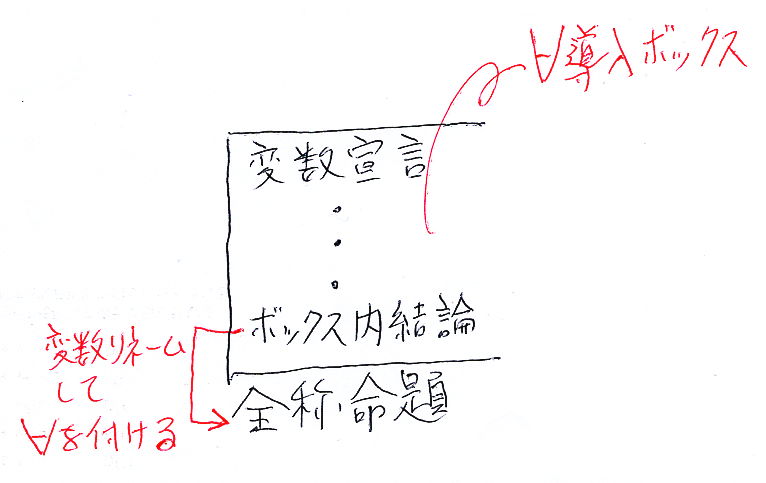
テキストと絵を混ぜるのは大変なので、∀導入ボックスをテキストで表現するには:
BEGIN ∀導入 変数宣言 : : ボックス内結論 END ●全称命題
∀導入ボックス内で使う変数を、ボックス冒頭で宣言します。ボックス内結論に∀を付けて(全称束縛して)ボックスの外に出します。黒丸'●'は全称命題を目立たせるマーカーで、特に意味はありません。
具体例である「最小元の存在」の証明では、∀導入ボックス内の変数はxで、ボックス内結論 ∃z∈N.(a + z = x) に自由変数xが入っています。この自由変数xを束縛変数に書き換えて外に出すのですが、
- 慣れるまでは、自由変数と束縛変数に、別な名前を使うことを推奨。(前回述べた推奨事項)
もうこの推奨を破っています。同じ変数名xをそのまま束縛変数にも使っています。破っておいて言うのもナンですが、自由変数と束縛変数は本来別物なんですよ。構文的に完全に区別している例もあります。が、実際には文字が足りなくなるので、同じ名前を使い回すことになっちゃうんですね。
しかしそれでも、∀導入ボックス内で宣言された変数xは、ボックスの外部に絶対に漏れないことには注意してください。ボックス外のxは、たまたま同名の束縛変数であって、ボックス内のxがボックス外まで有効な(生きている)わけじゃないです。プログラミング言語で、ブロック内の変数が外から見えるわけないでしょ、それと同じ。
背理法も使ってみる: 最大元の非存在
前節で最小元を扱ったので、最大元もみておきましょう。最大の自然数は存在しないので、そのことを表現すれば:
- ¬∃a∈N.∀x∈N.(x ≦ a)
これを示すために次の命題を仮定します(後で証明します)。
- ∀x∈N.(x ≦ x + 1) ---(a)
- ∀x∈N.(x ≠ x + 1) ---(b)
この2つをまとめて書けば ∀x∈N.(x < x + 1) ですが、2つに分けた形にしておきます。
今度の証明要求は次のようになります。
- Γ |-? ¬∃a∈N.∀x∈N.(x ≦ a)
背理法を使うことにすれば:
- Γ, ∃a∈N.∀x∈N.(x ≦ a) |-? ⊥
'⊥'は矛盾を表す記号です。矛盾を出す証明は次のようになります。
証明要求: Γ, ∃a∈N.∀x∈N.(x ≦ a) |-? ⊥
●∃a∈N.∀x∈N.(x ≦ a)
BEGIN ∃除去
m∈N
∀x∈N.(x ≦ m)
--[∀除去 x:=m + 1]
m + 1 ≦ m ---(1)
∀x∈N.(x ≦ x + 1) ---$(a)
--[∀除去 x:=m]
m ≦ m + 1 ---(2)
// (1), (2)より
m + 1 ≦ m ∧ m ≦ m + 1 ---(3)
∀x, y∈N.(x ≦ y ∧ y ≦ x ⇒ x = y) ---$(反対称律)
--[∀除去 x:=m, y:=m + 1]
m ≦ m + 1 ∧ m + 1 ≦ m ⇒ m = m + 1 ---(4)
// (3), (4)より
m = m + 1 ---(5)
∀x∈N.(x ≠ x + 1) ---$(b)
--[∀除去 x:=m]
m ≠ m + 1 ---(6)
// (5), (6)より
⊥
END
⊥
変形後の証明要求の前提(左側)に「最大元が存在する」があるので、その最大元をmと置いて証明を進めています。∃除去ボックス内で遂行される証明は、既に分かっている全称命題の具体化(∀除去)ばっかりです。全称命題の具体化(∀除去)は、通常は無意識に行われています。
さて、補題(a), (b)ですが、あまりに明らかですからこれを公理にしてもいいですが、大小順序の定義と消約律から証明できます。不等号≦を、定義から存在命題に置き換えた形を証明要求としましょう。
証明要求: Γ |-? ∀x∈N.∃z∈N.(x + z = x + 1) BEGIN ∀導入 n∈N ∀x∈N.(x = x) ---$(等式の反射律) --[∀除去 x:=n + 1] n + 1 = n + 1 --[∃導入 左辺の1:←z] ∃z∈N.(n + z = n + 1) END ●∀x∈N.∃z∈N.(x + z = x + 1)
補題(b)を示すには、0 ≠ 1 が公理にあるとします。背理法を使う形の証明要求とします。
証明要求: Γ, x∈N, x = x + 1 |-? ⊥ // 前提から x = x + 1 // ゼロの中立性から x + 0 = x + 1 // 消約律から 0 = 1 // 公理 0 ≠ 1 と矛盾するので ⊥
おわりに
前回と今回で、∀導入, ∀除去, ∃導入, ∃除去、これら4つの推論規則の例をある程度は出せたと思います。特に、∀導入と∃除去では、ボックスを使います。ボックスには、そのボックス内でだけ有効な(生きている)変数が伴い、ボックスの先頭で変数宣言します。ボックスの入り口、出口にも決まったお作法があります。念の為再掲すると:

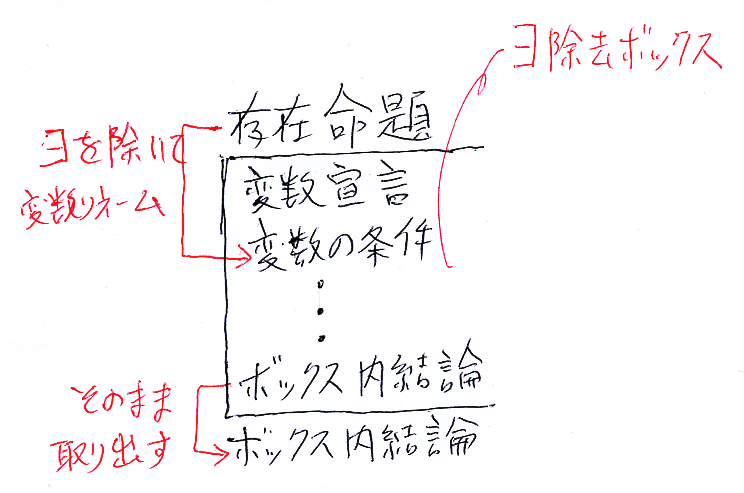
変数リネームは、(あまり守られない)推奨事項です。こういったボックスを意識すると、全称命題/存在命題を間違いなく扱うことが出来ます。