このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

フィードバック付きモノイド圏とその周辺

雑記／備忘

「だいたい圏になる： 概圏」において次のように書きました。

$`\mathcal{C}`$ から $`\mathcal{D}`$ を作る行為は、ダイアレクト構成〈dialect construction〉と呼ばれる構成法の一部です。

「ダイアレクト構成」に言及したものの、「それって何だっけ？」という気分だったので、ちょっと調べてみました。

比較的最近（2020年）のロマン〈Mario Román〉のノートから始めて、過去の論文を辿ってみました。ザッと眺めたところ、状況は思ったよりゴチャゴチャしてました。自分なりに整理してまとめておきます。出てくる概念（圏の種別）は次のようなものです。

  • フィードバック付きモノイド圏
  • トレース付きモノイド圏
  • 部分トレース付きモノイド圏
  • コンパクト閉圏

$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\In}{\text{ in } }
\newcommand{\Imp}{ \Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{－} }
%\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id} }
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Subject}{\Keyword{Subject } }%
`$
内容：

ロマンのノート

ロマンは次のノート〈おぼえ書き〉を書いています。

Work in progress と断りがあるとおり未完成のようで、なんか中途半端に終わっています。未完成のまま放置になるかも知れません。未完成でも貴重な情報が含まれたりするので、公開してくれるのはありがたいですね。

ロマンのノート[Rom20]の主題であるフィードバック付き圏〈category with feedback〉は、[KSW02]（ケイディズ／サバディーニ／ウォルタース 2002）として参照する以下の論文で導入されたものです。

これは昔読んだことがあります。この論文内にCirc構成〈サーキット構成〉という構成法が出てきますが、Circ構成とクライスリ構成（モナドからクライスリ圏を作ること）を組み合わせようとしていた痕跡が、2006年初頭のメモ書き日記にあります。

ロマンのノート[Rom20]では、[KSW02]の内容と手法を紹介して、拡張と応用を示唆しています。注目すべきは、Circ構成にコエンドを使っていることです。コエンドは、ここ数年のレンズ／オプティックの台頭でポピュラーになりましたが、それ以前に意識されることはなかったと思います。ロマンの定義を見て僕は「あっ、コエンドだったのか」とビックリしました。

ロマンのノート[Rom20]の最後は "5.4 Signal flow graphs" という見出しだけで、中身は何も書いてありません。続きの部分は次の論文としてまとめられたのかも知れません。

  • Title: Coinductive Streams in Monoidal Categories
  • Authors: Elena Di Lavore, Giovanni de Felice, Mario Román
  • Submitted: 30 Dec 2022
  • Pages: 57p
  • URL: https://arxiv.org/abs/2212.14494

なお、上記の2022年論文では、category with feedback を feedback monoidal category （feedbacked ではない）と呼んでいます。日本語なら「フィードバック付きモノイド圏」ですね。

バニョールの論文

「だいたい圏になる： 概圏」で言葉だけ出したダイアレクト構成〈dialect construction〉はCirc構成と似た（人によっては同じかも知れない）構成法です。「ダイアレクト構成」という言葉を使っている人は少ないようです。マーク・バニョール〈Marc Bagnol〉*1の以下の論文の第2節が "The dialect construction" です。

バニョールの[Bag15]の主題は部分トレース〈partial trace〉です。部分トレースは、圏論的オペレータであるトレースの一般化、あるいは弱くした概念です（後述します）。部分トレースは、GoI〈Geometry of Interaction〉との関連でハグヴァディ／スコット〈E. Haghverdi, P. J. Scott〉により2010年くらいに提案されたようです。次のマレハバ／スコット／セリンジャー〈Octavio Malherbe, Philip J. Scott, Peter Selinger〉論文に解説されています。

  • [MSS11]
  • Title: Partially traced categories
  • Authors: Octavio Malherbe, Philip J. Scott, Peter Selinger
  • Submitted: 19 Jul 2011 (v1), 4 Apr 2012 (v2)
  • Pages: 28p
  • URL: https://arxiv.org/abs/1107.3608

バニョールの[Bag15]は、[MSS11]の内容を要約整理して、部分トレース付きモノイド圏の表現定理（[MSS11]の第6節）のよりクリアな記述を与えています。部分トレース付き圏と全域トレース付き圏のあいだの関係を、アドホック随伴系における普遍性と普遍射で記述しています。

記法と用語の約束

まず、トレース付きモノイド圏〈traced monoidal category〉については知っているものとします。次の過去記事で述べています。

  1. トレース付き対称モノイド圏とはこんなモノ
  2. トレース付きモノイド圏の新しい定義
  3. トレースのタイトニングが自然変換であること
  4. こんな簡単なトレース付きモノイド圏があったなんて

他に関連しそうな記事のリストは：

トレース・オペレータは対称モノイド圏〈symmetric monoidal category〉に載るオペレータです。「対称性は当然に前提している」として、対称モノイド圏を単にモノイド圏と言っています。このテの省略は常に使われます。以下はだんだん省略される様です。

  • トレース付き対称モノイド圏
  • トレース付きモノイド圏（対称性は前提）
  • トレース付き圏（モノイド構造は前提）

また、多くの著者は厳密性を前提にしています。

  • トレース付き対称厳密モノイド圏
  • トレース付き対称モノイド圏（厳密性は前提）
  • トレース付きモノイド圏（対称性は前提）
  • トレース付き圏（モノイド構造は前提）

トレース・オペレータは次の等式的な公理を満たします。

  1. バニッシング（アクション性）
  2. タイトニング（自然性）
  3. スライディング
  4. スーパーポージング（強度性）
  5. ヤンキング

バニョールの論文[Bag15]では、アクション性をバニッシングと結合性〈associativity〉に分けて、公理を次のように分類しています（アクションの単位法則を分離する必要があった）。

  1. スーパーポージング（強度性）
  2. タイトニング（自然性）
  3. スライディング
  4. バニッシング（アクションの単位法則）
  5. 結合性（アクションの結合法則）
  6. ヤンキング

スライディング公理において、「同型射だけがスライドできる」に弱めた公理を弱スライディング公理〈weak sliding axiom〉と呼びます。スライディング公理の代わりに弱スライディング公理を要求したトレースを弱トレース〈weak trace〉と呼びます。

「弱トレースは実は通常のトレースである」という定理があります。これは、トレース付きモノイド圏の原典とも言えるジョイアル／ストリート／ヴェリティ〈A. Joyal, R. Street and D. Verity〉の論文の p.4 Lemma 2.1 です。

[JSV96] の Lemma 2.1 を（JSVの）増強補題〈enhancing lemma〉として参照します。与えられた弱いトレースを強くするからです。増強補題ではヤンキングを使っているので、ヤンキング公理がないと増強できません。

さまざな種類の構造付き圏を対象とする圏を次の固有名で呼ぶことにします。これらは“圏達の1-圏”であって“圏達の2-圏”ではありません。つまり、（恒等以外の）2-射は考えていません*2。これらの圏の射（構造付き関手）については後述します。

  • $`{\bf StMC}`$ ： 厳密モノイド圏達の圏
  • $`{\bf SStMC}`$ ： 対称厳密モノイド圏達の圏
  • $`{\bf TT\_SStMC}`$ ： トレース付き〈全域トレース付き〉対称厳密モノイド圏達の圏
  • $`{\bf PT\_SStMC}`$ ： 部分トレース付き対称厳密モノイド圏達の圏
  • $`{\bf Fbk\_SStMC}`$ ： フィードバック付き対称厳密モノイド圏達の圏
  • $`{\bf KCSStMC}`$ ： コンパクト閉対称厳密モノイド圏達の圏

長い名称を使いましたが、先に述べた流儀で省略・短縮されます。「コンパクト閉〈compact closed〉」に KC〈kompakt closed〉を使ったのは、「デカルト閉〈Cartesian closed〉」と間違われないようにです。対象である圏のサイズは小さくなくてもかまいませんが、局所小であることを要求します。

部分トレース付きモノイド圏

トレースの公理はすべて等式ですが、部分的な等式に置き換えたものが部分トレース〈partial trace〉です。部分的な等式は特殊な記号を使っているので、まずは部分トレースの公理の絵図版を示します（バニョール論文[Bag15]の画像コピー）*3。描画方向は、射の向きが左から右で、モノイド積の向きが下から上です。

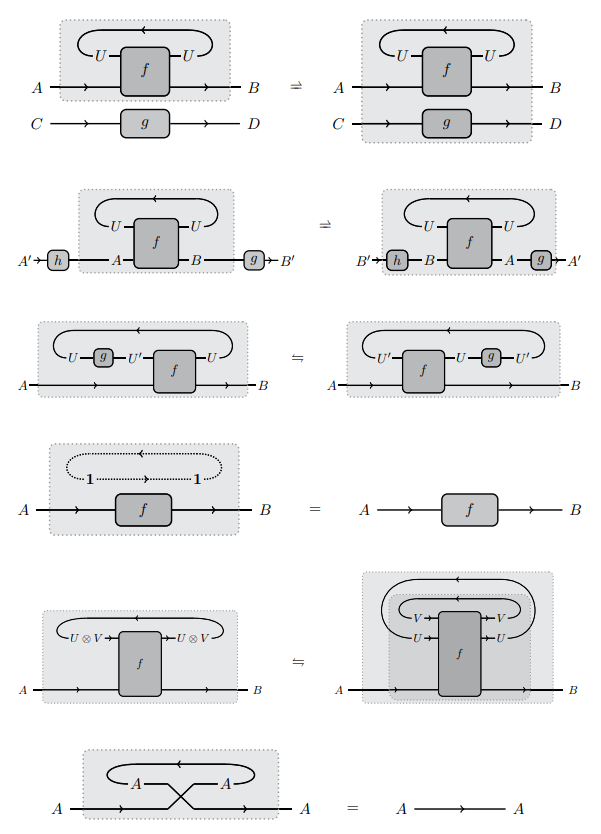
この図には三種類の等号が出てきます。

  1. 左から右の矢印（に似た記号）
  2. 両方向矢印（に似た記号）
  3. 通常の等号

それぞれ次の意味です。

  1. 左辺が定義されているならば右辺も定義されていて、かつ等しい。有向クリーネ等号〈directed Kleene equality〉と呼びます。
  2. 左辺が定義されていることと右辺が定義されていることは同値で、かつ等しい。クリーネ等号〈Kleene equality〉と呼びます。
  3. 左辺も右辺も全域的に定義されていて、かつ等しい。

部分トレースの定義では、トレースの法則ごとに等式の程度が違います。

  1. スーパーポージング： 左辺が定義されているなら右辺と等しい
  2. タイトニング： 左辺が定義されているなら右辺と等しい
  3. スライディング： 左右の定義域は同じで等しい
  4. バニッシング： 通常の等式
  5. 結合性： 左右の定義域は同じで等しい
  6. ヤンキング： 通常の等式

これらの部分等式的な公理を満たすオペレータ＝部分トレースを備えた対称モノイド圏が部分トレース付き対称モノイド圏〈partially traced symmetric monoidal category〉です。先に述べた省略・短縮の習慣により、部分トレース付き対称モノイド圏は、部分トレース付きモノイド圏、部分トレース付き圏とも呼びます。部分トレース付きモノイド圏と対比するときは、通常のトレース付きモノイド圏を全域トレース付きモノイド圏〈totally traced monoidal category〉とも呼びます。

部分トレースオペレータを（絵ではなく）テキストで表すときは次のように書きます。

$`\quad \mrm{Tr}^U_{A, B} : \cat{C}(A\otimes U, B\otimes U) \to \cat{C}(A, B)`$

下付きの $`A, B`$ はしばしば省略されて、次のように略記します。

$`\quad \mrm{Tr}^U[f] : A \to B \In \cat{C}`$

弱スライディング公理（同型射に限定したスライディング公理）は： $`f: A\otimes U' \to B\otimes U`$ と同型射 $`g: U \to U'`$ に関して次のように書けます。

$`\quad \mrm{Tr}^U[(\id_A \otimes g) ; f] \leftrightharpoons \mrm{Tr}^{U'}[f; (\id_B \otimes B)]`$

モノイド積の左右を区別するなら、右部分トレース・オペレータと左部分トレース・オペレータになりますが、台となる圏が対称モノイド圏なので、左右の区別をすることは稀です。しかし、人により右トレースを使うか左トレースを使うかはバラバラなので注意は必要です。

[注意]
線形代数や物理で出てくるトレース（行列の対角和で計算できる）は、値がスカラーになります。トレース付きモノイド圏の意味でのトレースも線形代数／物理内で定義できますが、これを部分トレース〈partial trace〉と呼ぶことがあります。つまり、この記事で出てきた部分トレースと、線形代数／物理の意味の部分トレースは意味がズレてしまっています。
[/注意]

部分トレース付きモノイド圏のあいだの射

モノイド圏を厳密と仮定したほうが扱いがはるかに楽だし、モノイド圏の厳密化定理〈一貫性定理〉から、厳密モノイド圏に限定しても“一般性は失わない”と言えるので、厳密モノイド圏ベースで考えます。厳密対称モノイド圏 $`\cat{C}`$ に載る部分トレースを $`\mrm{Tr}`$ で表します。部分トレース付きモノイド圏を一文字 $`\cat{C}`$ で表すなら、それを次のように表すべきでしょう。

$`\quad \cat{C} = (\underline{\cat{C}}, {^\cat{C}\mrm{Tr}}) \in |{\bf PT\_SStMC}|`$

ここで、$`\underline{\cat{C}} \in |{\bf SStMC}|`$ は台〈underlying thing〉である対称厳密モノイド圏です。

実際は、記号の乱用を使用します。

$`\quad \cat{C} = ({\cat{C}}, \mrm{Tr}) \in |{\bf PT\_SStMC}|`$

記号の乱用の問題点は、同一の台圏〈underlying category〉（正確には、台対称厳密モノイド圏）にたくさんの部分トレースが載る状況をうまく表せないことです。台圏 $`\cat{C}`$ に対して部分トレースが一意に決まるわけではありません。注意してください。

さて、部分トレース付きモノイド圏のあいだの射ですが、ベースは何らかのモノイド関手です。[KSW02]では、厳密モノイド関手をベースに考えてますが、これは制限が強すぎます。[MSS11]、[Bag15]では、タイト・モノイド関手をベースにしています。タイト・モノイド関手は通常「強モノイド関手」と呼ばれますが、「強」は「テンソル強度を保存する」の意味で使いたいので、「タイト」を使っています。

タイト・モノイド関手は、モノイド関手の乗法ラクセイターと単位ラクセイター（「緩化子〈ラクセイター〉」参照）が同型射であるモノイド関手です。さらに対称性があるのでタイト対称モノイド関手〈対称タイト・モノイド関手〉を考えます。タイト対称モノイド関手の定義は、「この2つのミニマムな解説はほんとに便利だ」で紹介したバエズの"Should know"などを見てください。

台圏のあいだのタイト・モノイド関手 $`F`$ に対して、部分トレースに関する振る舞いを要求して、部分トレース付きモノイド圏のあいだの射〈morphism between partially traced monoidal categories〉を定義します。部分トレースに関する条件はかなりキツイものです。その条件とは「厳密に部分トレースを保存・反映する〈strictly preserves and reflects partial trace〉」です。

$`(\cat{C}, {^\cat{C}\mrm{Tr}}), (\cat{D}, {^\cat{D}\mrm{Tr}})`$ が2つの部分トレース付き圏だとして、タイト・モノイド関手 $`F: \cat{C} \to \cat{D} \In {\bf SStMC}`$ が満たすべき条件は：

  • $`{^\cat{C}\mrm{Tr}}^U_{A, B}(f) = g`$ が $`\cat{C}`$ で成立しているならば、$`{^\cat{D}\mrm{Tr}}^{F(U)}_{F(A), F(B)}(F(f)) = F(g)`$ が $`\cat{D}`$ で成立する。
  • $`{^\cat{D}\mrm{Tr}}^{F(U)}_{F(A), F(B)}(F(f)) = F(g)`$ が $`\cat{D}`$ で成立しているならば、$`{^\cat{C}\mrm{Tr}}^U_{A, B}(f) = g`$ が $`\cat{C}`$ で成立する。

上記の条件を満たすタイト対称モノイド関手を射とする圏 $`{\bf PT\_SStMC}`$ が定義できます。“全域トレース付きモノイド圏の圏” $`{\bf TT\_SStMC}`$ は $`{\bf PT\_SStMC}`$ の充満部分圏になります。射の定義は同じです。

“圏達の圏”の射をまとめておくと：

  • $`{\bf StMC}`$ の射： タイト・モノイド関手
  • $`{\bf SStMC}`$ の射： 対称タイト・モノイド関手
  • $`{\bf PT\_SStMC}`$ の射： 厳密に部分トレースを保存・反映する対称タイト・モノイド関手
  • $`{\bf TT\_SStMC}`$ の射： 厳密に全域トレースを保存・反映する対称タイト・モノイド関手

フィードバック付きモノイド圏達の圏

フィードバック付きモノイド圏〈monoidal category with feedback | feedback monoidal category〉は、トレース付きモノイド圏とよく似た構造です。トレース・オペレータの代わりにフィードバック・オペレータ〈feedback operator〉が付きます。フィードバック・オペレータとトレース・オペレータの違いは次のニ点です。

  1. ヤンキング公理を要求しない。
  2. スライディング公理の代わりに弱スライディング公理を要求する。

先に、弱スライディング公理から（通常の）スライディング公理を出せる（JSVの増強補題）、と言いましたが、それはヤンキング公理があるからで、フィードバック・オペレータの場合は弱スライディング公理からスライディング公理は従いません。

フィードバック付きモノイド圏を、記号の乱用を使って次のように書きます。

$`\quad \cat{C} = (\cat{C}, \mrm{Fbk})`$

台〈underlying thing〉としての $`\cat{C}`$ は対称厳密モノイド圏で、$`\mrm{Fbk}`$ はフィードバック・オペレータです。

フィードバック付きモノイド圏のあいだの射は部分トレース付きモノイド圏の場合と同じです。つまり、$`(\cat{C}, {^\cat{C}\mrm{Fbk}}), (\cat{D}, {^\cat{D}\mrm{Fbk}})`$ が2つのフィードバック付きモノイド圏だとして、タイト・モノイド関手 $`F: \cat{C} \to \cat{D} \In {\bf SStMC}`$ がフィードバック付きモノイド圏のあいだの射〈morphism between feedback monoidal categories〉である条件は：

  • $`{^\cat{C}\mrm{Fbk}}^U_{A, B}(f) = g`$ が $`\cat{C}`$ で成立しているならば、$`{^\cat{D}\mrm{Fbk}}^{F(U)}_{F(A), F(B)}(F(f)) = F(g)`$ が $`\cat{D}`$ で成立する。
  • $`{^\cat{D}\mrm{Fbk}}^{F(U)}_{F(A), F(B)}(F(f)) = F(g)`$ が $`\cat{D}`$ で成立しているならば、$`{^\cat{C}\mrm{Fbk}}^U_{A, B}(f) = g`$ が $`\cat{C}`$ で成立する。

フィードバック付きモノイド圏を対象として、上記のようなタイト・モノイド関手を射とする圏を $`{\bf Fbk\_SStMC}`$ とします。

State構成とその変種

一般に、圏 $`\cat{C}, \cat{D}`$ に対して、$`|\cat{C}| \to |\cat{D}|`$ という写像を構成法とか構成〈construction〉と呼びます。射の集合のあいだの写像 $`\mrm{Mor}(\cat{C}) \to \mrm{Mor}(\cat{D})`$ も定義できて、全体として関手になるときは、関手的構成法〈functorial construction〉です*4。この記事に出てくる構成には関手的に出来るものもありますが、その点には言及していません。

ここでのState構成は次の形の写像です。

$`\quad \mrm{State} : |{\bf SMC}| \to |{\bf SMAC}|`$

ここで、$`{\bf SMAC}`$ は対称モノイド概圏〈symmetric monoidal almost category〉達の圏です。概圏は、「だいたい圏になる： 概圏」で述べたように次のニ点で圏〈局所小圏〉とは異なります。

  1. ホムセットが小さいとは限らない。
  2. 結合演算に関する法則が、合同（都合が良い同値関係）によって記述される。

State構成は、「だいたい圏になる： 概圏」と「概圏の事例（整理して再度）」における「状態付き射の圏」を作る手順と同じ構成法です。ただし、作った概圏にモノイド構造を入れて、モノイド概圏にします。バニョールの[Bag15]では、Stete構成で得られた $`\mrm{Sate}(\cat{C})`$ をダイアレクト圏〈dialect category〉と呼んでいます。

構成したモノが圏ではない概圏であるのは嬉しくないので、条件を付けて圏が生成されるようにします。まず、素材〈入力〉は対称厳密モノイド圏に限定します。圏の法則に対する合同は不要になり等式だけで済みます。次に、素材の圏は本質的に小さい〈essentially small〉とします。すると、とある合同（すぐ後に記述）による商圏〈quotient category〉は局所小かつ本質的に小さい圏になります。この状況でのState構成は次のようです（St は strict monoidal から、EsC は essentially small category）。

$`\quad \mrm{StEsState} : |{\bf SStMEsC}| \to |{\bf SStMEsC}|`$

記法を簡略化するために、一時的に $`\widehat{\cat{C}} := \mrm{State}(\cat{C})`$ と置きます。対象集合は $`|\widehat{\cat{C}}| = |\cat{C}|`$ と共有されて、$`\widehat{C}`$ のホムセットは次のようです。

$`\For A, B \in |\widehat{\cat{C}}| = |\cat{C}|\\
\Define \widehat{\cat{C}}(A, B) := \sum_{U\in |\cat{C}|} \cat{C}(A\otimes U, B\otimes U)
`$

ここで、$`\sum`$ は集合族〈ファミリー〉の総直和（シグマ型）を表します。総直和の要素は、$`(U, f)`$ のような依存ペアになります。

$`\quad F \in \widehat{\cat{C}}(A, B)\\
\Iff F = (U, f) \:\text{ for some }U\in |\cat{C}|,\; f:A\otimes U\to B\otimes U \In \cat{C}
`$

しかし、ほとんどの場合、記号の乱用が使われます。

$`\quad f = (U, f) \:\text{ for some }U\in |\cat{C}|,\; f:A\otimes U\to B\otimes U \In \cat{C}`$

$`\cat{C}`$ が小さくない圏のとき、上記ホムセットも小さくない集合になります。ホムセット $`\widehat{\cat{C}}(A, B)`$ に次の関係を入れます。同じ定義（厳密モノイド圏とは限らない場合）は「概圏の事例（整理して再度）」にもあります。

$`\For \varphi :U \to U' \text{ isomorphism }\In \cat{C}\\
\For (U, f), (U', f') \in \widehat{\cat{C}}(A, B)\\
\Define (U, f) \sim^g_{A, B} (U', f') :\Iff\\
\quad f = (\id_A \otimes \varphi);f';(\id_B \otimes \varphi^{-1}) \;: A\otimes U' \to B\otimes U' \In \cat{C}
`$

すべての同型 $`\varphi`$ に渡ってこれらの関係を寄せ集めて、その関係が生成する最小の同値関係を $`\sim_{A, B}`$ とします（今のこのケースでは、最小の同値関係の生成手順は省略できます）。同値関係の族 $`(\sim_{A, B})_{A, B\in |\widehat{\cat{C}}|}`$ は $`\widehat{\cat{C}}`$ 上の合同になります。

構成 $`\mrm{StEsState}`$ は次のように定義されます。

$`\For \cat{C} \in |{\bf SStMEsC}|\\
\Define |\mrm{StEsState}(\cat{C})| := |\cat{C}|\\
\For A, B \in |\mrm{StEsState}(\cat{C})|\\
\Define \mrm{StEsState}(\cat{C})(A, B) := \widehat{\cat{C}}(A, B)/\!\sim_{A, B} \,= \mrm{State}(\cat{C})(A, B)/\!\sim_{A, B}
`$

上記の定義は、対象の集合とホムセットしか定義してませんが、諸々の作業を行って次が分かります。

  • $`\cat{C}`$ が本質的に小さいなら、$`\mrm{StEsState}(\cat{C})`$ は局所小である。
  • $`\cat{C}`$ が本質的に小さいなら、$`\mrm{StEsState}(\cat{C})`$ も本質的に小さい。
  • $`\mrm{StEsState}(\cat{C})`$ に厳密モノイド構造が入る。
  • $`\cat{C}`$ を $`\mrm{StEsState}(\cat{C})`$ に、厳密モノイド構造を保って充満に埋め込める。

ロマンのノート[Rom20]では、ホムセット $`\widehat{\cat{C}}(A, B)/\!\sim_{A, B}`$ の構成にコエンドを使っています。これは非常に面白いですが、別の機会に取り上げることにします。

FbkMC構成

与えられた対称厳密モノイド圏 $`\cat{C} \in |{\bf SStMC}|`$ に対して $`\mrm{StEsState}(\cat{C})`$ は、それだけでも（追加構造なしでも）意味があります。が、$`\mrm{StEsState}(\cat{C})`$ にフィードバック・オペレータを追加すると応用上は便利です。

対称厳密モノイド圏 $`\cat{C}`$ からフィードバック付きモノイド圏を作る構成を $`\mrm{FbkMC}`$ とします。前節の $`\mrm{StEsState}`$ 構成とは次のような関係になります。

$`\require{AMScd}
\begin{CD}
|{\bf SStMC}| @>{\mrm{FbkMC}}>> |{\bf Fbk\_SStMC}|\\
@| @VV{\mathbb{U}_\mrm{obj}}V\\
|{\bf SStMC}| @>{\mrm{StEsState}}>> |{\bf SStMC}|
\end{CD}\\
\text{commutative in }{\bf SET}
`$

ここで、$`\mathbb{U}_\mrm{obj}`$ は、忘却関手の対象パートです。つまり、FbkMC構成で作ったフィードバック付きモノイド圏からフィードバック・オペレータを忘れると、StEsState構成で作ったモノイド圏になります。

忘却関手 $`\mathbb{U} : {\bf Fbk\_SStMC} \to {\bf SStMC}`$ に対して、FbkMC構成は自由対象の構成法になっています。このことは、バニョールの[Bag15]で強調されていることですが、今日はこれ以上触れません。

記法の簡略化のために、一時的に $`\overline{\cat{C}} := \mrm{FbMC}(\cat{C})`$ と置きます。$`\overline{\cat{C}}`$ にはフィードバック・オペレータが付いているので、次のように書けます。

$`\quad \overline{\cat{C}} = (\mrm{StEsState}(\cat{C}), {^\overline{\cat{C}}\mrm{Hd}} )`$

$`{^\overline{\cat{C}}\mrm{Hd}}`$ はフィードバック・オペレータですが、プログラミングとの対比でいうと情報隠蔽〈information hiding〉に相当するので、綴りを hiding から取っています。記号の乱用では次のように書きます。

$`\quad \overline{\cat{C}} = (\overline{\cat{C}}, \mrm{Hd} )`$

$`\mrm{Hd}`$ オペレータの成分は以下のように定義します。$`\Subject`$で、定義すべきモノを宣言してから実際の定義を続けます。同値類は（ブラケットではなくて）山形括弧で表します。ブラケットは、オペレータへの引数を入れる括弧です。

$`\For A, B, U \in |\overline{\cat{C}}|\\
\Subject \mrm{Hd}^U_{A, B} : \overline{\cat{C}}(A\otimes U, B\otimes U) \to \overline{\cat{C}}(A, B)\\
\For f: (A\otimes U) \otimes S \to (B \otimes U) \otimes S \In \cat{C}\\
\Define \mrm{Hd}^U_{A, B}[ \langle S, f\rangle ] := \langle U\otimes S, f\rangle
`$

この定義は同値類の代表元を使っているので、代表元の選び方によらないことを確認する必要があります。また、$`\mrm{Hd}`$ が全体としてフィードバックの公理を満たすことも証明が必要です。これらの作業を済ませると次が言えます。

  • 対称厳密モノイド圏 $`\cat{C}`$ から作った $`\overline{\cat{C}} = (\overline{\cat{C}}, \mrm{Hd} )`$ はフィードバック付きモノイド圏になる。

前節のState構成とその変種は、与えられた対称厳密モノイド圏から別な対称厳密モノイド概圏／対称厳密モノイド圏を作るだけでした。それに対してFbkMC構成はフィードバック付きモノイド圏を作ります。

Circ構成とダイアレクト構成

Circ構成／サーキット構成〈{Circ | Circuit} construction〉、ダイアレクト構成〈dialect construction〉は、多くの場合前節のFbkMC構成と同じ構成法を意味します。が、StEsState構成のようなState構成の変種のこともCirc構成／ダイアレクト構成と呼ぶこともあります。

State構成でできる概圏、または合同で商をとった厳密概圏の射はサーキット〈circuit〉と呼びます。よって、Circ構成／ダイアレクト構成で作られる圏はサーキットの圏〈category of circuits〉とも呼びます。「サーキット」は「状態付き射」と同義語です。

もとになる圏が幾つかの仮定を満たせば、サーキットの圏は局所小な対称厳密モノイド圏になり、フィードバック・オペレータを持つことになります。

[追記]
トレース付きモノイド圏に関しては、長谷川さんの次の論文は役に立ちます。

次の論文に、トレース付き／フィードバック付きモノイド圏によるオートマトンとサーキットの分析があります。

線形論理と証明ネットに興味があるなら：

[/追記]

CPT構成

$`\cat{C} = (\cat{C}, \mrm{Tr})`$ （記号の乱用）が部分トレース付きモノイド圏だとします。台圏（正確には台対称厳密モノイド圏）としての $`\cat{C}`$ にFbkMC構成をした結果であるフィードバック付きモノイド圏を（またしても記号の乱用で）次のように書きます。

$`\quad \mrm{FbkMC}(\cat{C}) = \overline{\cat{C}} = (\overline{\cat{C}}, \mrm{Hd})`$

$`\overline{\cat{C}}`$ は $`\cat{C}`$ のサーキットの圏です。サーキットの圏 $`\overline{\cat{C}}`$ に対して、部分トレース $`\mrm{Tr}`$ を使うことによって合同 $`\approx`$ を定義できます。サーキットの圏上の合同の作り方についてはバニョールの[Bag15]を見てください。

$`\overline{\cat{C}}`$ 上の合同 $`\approx`$ は部分トレース $`\mrm{Tr}`$ に依存して定義されるので、部分トレースによる合同〈congruence by partial trace | CPT〉と呼ぶことにします。必要があれば、$`\approx_{\mrm{Tr}}`$ のように部分トレースを添えます。また、$`\overline{\cat{C}}`$ から合同付き圏 $`(\overline{\cat{C}}, \approx_{\mrm{Tr}})`$ を作る構成はCPT構成〈CPT construction〉と呼びましょう。

$`\quad |{\bf Fbk\_SStMC}|\ni \overline{C} \:\overset{\mrm{CPT}}{\mapsto}\; (\overline{\cat{C}}, \approx_{\mrm{Tr}}) \in |{\bf C\_SStMC}|`$

ここで、$`{\bf C\_SStMC}`$ は合同が付いた（亜集合で豊穣化された）対称厳密モノイド圏達の圏です（射を適切に定義する必要がありますが）。合同付き対称厳密モノイド圏の商圏〈quotient category〉を作ることができます。一般には、もとの圏の対称厳密モノイド構造を商圏に落とせる保証はないですが、この場合はうまいこと商圏も対称厳密モノイド圏になってくれます。したがって、以下の図のCPTQ構成が定義できます。（商圏を作る構成はQ構成です。）

$`\begin{CD}
|{\bf Fbk\_SStMC}| @>{\mrm{CPT}_{\mrm{Tr}} }>> |{\bf C\_SStMC}|\\
@| @VV{Q}V\\
|{\bf Fbk\_SStMC}| @>{\mrm{CPTQ}_{\mrm{Tr}} }>> |{\bf SStMC}|\
\end{CD}\\
\text{commutative in }{\bf SET}
`$

ここで重要な事実は、$`\mrm{CPTQ}_\mrm{Tr} (\overline{C})`$ 上にフィードバック・オペレータ $`\mrm{Hd}`$ を落とせることです。この点についても、詳細はバニョールの[Bag15]を見てください。商圏に落とした $`\mrm{Hd}`$ を同じ記号で書くとして、次が成立します。

  • $`\mrm{Hd}`$ は、$`\mrm{CPTQ}_\mrm{Tr} (\overline{C})`$ 上の全域弱トレースになる。
  • JSVの増強補題により、全域弱トレースは全域トレースに増強できるので $`\mrm{Hd}`$ は全域トレースだと思ってよい。
  • 部分トレース付き圏 $`(\cat{C}, \mrm{Tr})`$ は、全域トレース付き圏 $`(\mrm{CPTQ}_\mrm{Tr} (\overline{C}), \mrm{Hd})`$ にトレースを保って規準的に埋め込める。
  • 上記の、部分トレース付き圏から全域トレース付き圏を作る構成は、忘却関手に関して普遍的である。

これらのことは、マレハバ／スコット／セリンジャーの[MSS11]とバニョールの[Bag15]の主要なトピックです。

最小トレース

前節のCPTQ構成（CPT構成の後で商圏を作る構成）は、与えられた部分トレース付き圏 $`(\cat{C}, \mrm{Tr})`$ から、全域トレース付き圏 $`(\mrm{CPTQ}_\mrm{Tr} (\overline{C}), \mrm{Hd})`$ を作ります。したがって、CPTQ構成の域〈ソース | 入力集合〉は $`|{\bf PT\_SStMC}|`$ です。単なる対称厳密モノイド圏をCPTQ構成（の第一段階であるCPT構成）に渡すことはできません。ホムセット上の同値関係の構成に部分トレース $`\mrm{Tr}`$ を使いますから。

しかし、素の〈プレーンな〉対称厳密モノイド圏 $`\cat{C}`$ が与えられたとき、“自明な部分トレース” を添えることができます。部分トレースを、その定義域の大きさで順序付けると、“自明なトレース”は最小になるので、最小トレース〈minimum trace〉と呼ぶことにします。

最小トレース $`\mrm{MTr}`$ は以下のように定義します。（[追記]厳密モノイド圏なら、$`\mrm{MTr}^I`$ は何もしなくていいですね、一般のモノイド圏の場合を書いてしまいました。が、このまま残します。[/追記]）

$`\For A, B \in |\cat{C}|\\
\Subject \mrm{MTr}^I_{A, B} : \cat{C}(A\otimes I, B\otimes I) \to \cat{C}(A, B)\\
\For f \in \cat{C}(A\otimes I, B\otimes I)\\
\Define \mrm{MTr}^I_{A, B}[f]:= {\rho_A}^{-1} ; f ; \rho_B \;\in \cat{C}(A, B)\\
\:\\
\For A \in |\cat{C}|\\
\Subject \mrm{MTr}^A_{A, A} : \cat{C}(A\otimes A, A\otimes A) \supseteq\!\to \cat{C}(A, A)\\
\For \sigma_{A, A} \in \cat{C}(A\otimes A, A\otimes A)\\
\Define \mrm{MTr}^I_{A, B}[\sigma_{A, A}]:= \id_A \;\in \cat{C}(A, A)
`$

つまり、この部分トレース・オペレータは、$`f:A\otimes I\to B\otimes I`$ という形の射と対称射 $`\sigma_{A, A}`$ に対してしか定義されていません。その他の射には対しては未定義です。それでも、バニッシング法則（アクションの単位法則）とヤンキング法則を満たすので、部分トレースの条件はクリアしてます。

任意の対称厳密モノイド圏 $`\cat{C}`$ に対して、最小トレースを付けて $`(\cat{C}, \mrm{MTr})`$ を作る構成を $`\mrm{MTrMC}`$ （minimum traced monoidal category から）とします。これは自由構成になっていて、次のようなアドホック随伴系を形成します。

$`\quad {\bf PT\_SStMC}(\mrm{MTrMC}(\cat{C}), \cat{D}) \cong {\bf SStMC}(\cat{C}, \mathbb{U}(\cat{D} ) )`$

ここで、$`\mathbb{U}`$ は忘却関手です。$`\mrm{MTrMC}`$ は関手として定義されているわけではないので、完全な随伴系にはなりませんが、$`\cat{C}`$ を選ぶたびにその自由対象をアドホックに〈都度都度〉構成できます。

$`\mrm{MTrMC}`$ と $`\mrm{CPTQ}`$ をこの順で繋げば、任意の対称厳密モノイド圏から全域トレース付きモノイド圏を作り出す構成が得られます。

Int構成

Int構成〈Int construction〉は、与えられたトレース付きモノイド圏〈全域トレース付き対称厳密モノイド圏〉から、コンパクト閉圏を作り出す構成です。つまり：

$`\quad \mrm{Int}: |{\bf TT\_SStMC}| \to |{\bf KCSStMC}| \In {\bf SET}`$

Int構成は、ジョイアル／ストリート／ヴェリティの[JSV96]で既に述べられています。ジラール（Jean-Yves Girard）のGoI〈Geometry of Interaction〉で使われた事情からGoI構成〈GoI construction〉とも呼ばれます。

Int構成〈GoI構成〉については、以下の過去記事でも述べているので、説明は割愛します。

$`\mrm{MTrMC}`$ と $`\mrm{CPTQ}`$ と $`\mrm{Int}`$ をこの順で繋げば、任意の対称厳密モノイド圏からコンパクト閉圏を作り出す構成が得られます。この構成法はかなり回りくどいので、もっと直接的な（短絡した）構成法もあります。例えば、次の白旗さんの論文を参照してください。

おわりに

対称厳密モノイド圏から出発して、コンパクト閉圏〈コンパクト閉対称厳密モノイド圏〉を得ることができます。その中間段階で、次のような種類の圏を経由します。

  1. 対称厳密モノイド圏
  2. 部分トレース付きモノイド圏
  3. フィードバック付きモノイド圏
  4. トレース付きモノイド圏
  5. コンパクト閉圏

モノイド圏の厳密性の仮定は便宜的なもので、外すことができます（代わりに議論が複雑化しますが）。律儀にこの構成のプロセスをたどる必要はなくて、短絡する〈近道する | バイパスする〉方法はあります。どのような構成法を使ったにしても、得られる圏は、構造付きの圏同値の意味で一意的です。

ということは、上に列挙した様々な圏達は、親族的関係性にあるということです。コンパクト閉圏は、他の種別の圏への忘却関手を持ちます。一方で、一番構造に乏しい対称モノイド圏も、他の種別の圏になり得る“素質”を備えています。素朴な対称モノイド圏にも、親族が共有する遺伝子として、トレース・オペレータやコンパクト閉構造のタネが仕込まれています。

*1:Bagnol の発音はよくわかりません。フランス語読みだと「バニョール」に近いようです。

*2:圏同値を考えるためには2-射が必要です。が、今回は圏同値には触れません。

*3:バニッシング（アクションの単位法則）の絵がちょっと変です。左辺点線のループは、$`f`$ の箱から出るべきでしょう。

*4:関手的構成法は、定義から関手そのものです。が、先に対象に対する構成法があって、それを拡張したときは関手的構成法と呼ぶのがふさわしいでしょう。