半グラフの二重圏と半グラフ変形 - 檜山正幸のキマイラ飼育記 (はてなBlog)

ここのところ、半グラフに関する記事を幾つか書いています。それらは、次のハブ記事から参照できます。

スケマティック系のハブ記事 // 半グラフ

すべての半グラフ達により形成される社会は、いったいどういう構造なのだろう？と考えてみると；圏でも2-圏でも不十分なようです。すべての半グラフ達は二重圏を形成するとみなすのが良いと思います。つまり、“半グラフのあいだの射”と呼べるものが二種類 -- 縦射と横射があることになります。

ボリソフ／マニン〈D. Borisov, Yu. I. Manin〉、コステロ〈Kevin Costello〉、バーガー／カウフマン〈Clemens Berger, Ralph M. Kaufmann〉などが扱っている半グラフの圏は、半グラフの二重圏の横方向だけを取り出したものだと解釈できます。

この記事では、半グラフの二重圏の枠組みをセットアップして、その横1-射（半グラフ変形と呼ぶ）を、従来より操作的・手続き的〈operational/procedural〉に定義することにします。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\bdry}{\partial }
\newcommand{\Imp}{\Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\slt}{\mathrel{\dot{\lt}}}% successor lt
\newcommand{\pto}{\not\to }% pro arrow
`$

内容：

半グラフ
半グラフ射
半グラフ二重圏
半グラフ・プロ射／半グラフ変形
半グラフ変形の指令半グラフ
おわりに
追記：頂点同一視

半グラフ

半グラフとその圏については、以下の3つの論文を参考にします。

[BM06-11]
Title: Generalized operads and their inner cohomomorphisms
Authors: D. Borisov, Yu. I. Manin
Submitted: 27 Sep 2006 (v1), 7 Jan 2011 (v5)
Pages: 71p
URL: https://arxiv.org/abs/math/0609748

[Cos04-04]
Title: The A-infinity operad and the moduli space of curves
Author: Kevin Costello
Submitted: 2 Feb 2004 (v1), 15 Sep 2004 (v2)
Pages: 14p
URL: https://arxiv.org/abs/math/0402015

[BK22-]
Title: Trees, graphs and aggregates: a categorical perspective on combinatorial surface topology, geometry, and algebra
Authors: Clemens Berger, Ralph M. Kaufmann
Submitted: 25 Jan 2022
Pages: 48p
URL: https://arxiv.org/abs/2201.10537

半グラフは、ボリソフ／マニンの定義に従います（その他の定義については「半グラフの様々な定義」参照）。コステロもバーガー／カウフマンもボリソフ／マニン半グラフを扱っています。

半グラフに関する用語・記法は、上記3つの論文で少しずつ違いますが、ここでは、半グラフの構成素は次のように書きます。

頂点〈vertex〉の集合： $`V`$
半辺〈half-edge〉の集合： $`H`$
境界写像〈boundary map〉： $`\bdry : H \to V`$
ペアリング対合〈pairing involution〉： $`\iota : H \to H`$ （ペアリング対合とパートナー指定対合〈partner designation involution〉は同じものです。）

半グラフを表すにはギリシャ文字アルファベット前半の小文字 $`\alpha, \beta, \gamma`$ などを使います。半グラフのインスタンスは次のように記述します。

$`\quad \alpha = (V(\alpha), H(\alpha), \bdry_\alpha, \iota_\alpha)`$

ちなみに、ボリソフ／マニン、コステロ、バーガー／カウフマンはそれぞれ、次の記法を使っています。

ボリソフ／マニン： $`\tau = (F_\tau, V_\tau, \bdry_\tau, j_\tau)`$ （$`F`$ はフラグ〈半辺〉）
コステロ： $`\gamma = (V(\gamma), H(\gamma), \pi, \sigma)`$
バーガー／カウフマン： $`\Gamma = (V_\Gamma, F_\Gamma, \bdry_\Gamma, \iota_\Gamma)`$

半グラフ $`\alpha`$ に関連する集合として次も使います。

辺〈edge〉の集合： $`E`$
テール〈tail〉の集合： $`T`$
内部辺〈internal edge〉の集合： $`\mrm{Int}E`$
外部辺〈external edge〉の集合： $`\mrm{Ext}E`$
連結成分〈connected component〉の集合： $`C`$

辺とは、半辺の集合 $`H`$ をペアリング対合が誘導する同値関係で割った同値類のことです。同値類が二元集合であるとき内部辺、同値類が単元集合であるとき外部辺です。連結成分は、頂点集合を「パスで結ばれるなら同値」という同値関係で割った同値類です。

半グラフ射

ボリソフ／マニンとバーガー／カウフマンの半グラフの圏を $`{\bf Gr}`$ とします。コステロの半グラフの圏は $`{\bf Graphs}`$ です。これから定義する半グラフの圏 $`{\bf SemiGraphC}`$ は、$`{\bf Gr}`$ とも $`{\bf Graphs}`$ とも違います。

半グラフの構造は、次の図式で表現できます。

$`\quad \xymatrix{
% @(inDir, outDir)
H \ar@(ul, dl)[0,0]_{\iota} \ar[r]^{\bdry}
& V
}
`$

上記の図式〈有向グラフ〉から自由生成される圏に、$`\iota`$ が対合であること、つまり $`\iota; \iota = \mrm{id}_H`$ を関係として入れると、恒等射を含めて5つの射からなる圏ができます。この2対象5射の圏を $`{\bf semigraph}`$ とします。

半グラフのインスタンス $`\alpha`$ は、圏 $`{\bf semigraph}`$ から集合圏 $`{\bf Set}`$ への関手です。

$`\quad \alpha : {\bf semigraph} \to {\bf Set} \In {\bf CAT}\\
\text{where}\\
\quad \alpha(V) := V(\alpha) \;\in |{\bf Set}|\\
\quad \alpha(H) := H(\alpha) \;\in |{\bf Set}|\\
\quad \alpha(\bdry) := \bdry_\alpha \;: \alpha(H) \to \alpha(V) \In {\bf Set}\\
\quad \alpha(\iota) := \iota_\alpha \;: \alpha(H) \to \alpha(H) \In {\bf Set}
`$

関手の記法だと $`\alpha(V)`$ なのに、$`V(\alpha)`$ と書くと約束しました。なんか奇妙ですが、単に書き方の問題なので気にしない。“書き方の問題”については以下の記事を参照してください。

構造とその素材の書き表し方

半グラフのあいだの射は自然変換だと定義すると、関手圏〈余前層の圏*1〉として半グラフの圏を定義できます。

$`\quad {\bf SemiGraphC} := [{\bf semigraph}, {\bf Set}] = {\bf CAT}({\bf semigraph}, {\bf Set})`$

末尾の 'C' は category のつもりで、後で半グラフの亜群や二重圏も定義するので区別するためです。

半グラフのあいだの射を $`f:\alpha \to \beta`$ とすると、$`f = (f_V, f_H)`$ は自然変換なので、次の図式を可換にします。

$`\require{AMScd}
\quad \begin{CD}
H(\alpha) @<{\iota_\alpha}<< H(\alpha) @>{\bdry_\alpha}>> V(\alpha) \\
@V{f_H}VV @V{f_H}VV @VV{f_V}V\\
H(\beta) @<{\iota_\beta}<< H(\beta) @>{\bdry_\beta}>> V(\beta) \\
\end{CD}\\
\quad \text{commutative in }{\bf Set}
`$

関手・自然変換の記法で書くなら（まったく同じことですが）：

$`\require{AMScd}
\quad \begin{CD}
\alpha(H) @<{\alpha(\iota)}<< \alpha(H) @>{\alpha(\bdry)}>> \alpha(V) \\
@V{f_H}VV @V{f_H}VV @VV{f_V}V\\
\beta(H) @<{\beta(\iota)}<< \beta(H) @>{\beta(\bdry)}>> \beta(V) \\
\end{CD}\\
\quad \text{commutative in }{\bf Set}
`$

圏 $`{\bf SemiGraphC}`$ のすべての同型射〈可逆射〉からなる広い部分圏を $`{\bf SemiGraphG}`$ とします。末尾の 'G' は groupoid のつもりです。圏 $`{\bf SemiGraphC}`$ の射を半グラフ射〈semi-graph morphism〉と呼びます。$`{\bf SemiGraphG}`$ の射も半グラフ射ですが、「コステロの半グラフ圏から二重関手意味論へ」では半グラフのアルファ変換〈alpha conversion〉と呼んでいます。

半グラフ二重圏

「コステロの半グラフ圏から二重関手意味論へ // コステロの半グラフ圏はいったい何なのか？」で述べたように、半グラフ達の二重圏を考えるのが良さそうです。その半グラフ二重圏〈semi-graph double category | double category of semi-graphs〉を $`{\bf SemiGraphDC}`$ とします。末尾の 'DC' は double category からです。ボリソフ／マニンおよびバーガー／カウフマンの圏 $`{\bf Gr}`$ も、コステロの圏 $`{\bf Graphs}`$ も、半グラフ二重圏 $`{\bf SemiGraphDC}`$ に埋め込むことができます。

半グラフ二重圏 $`{\bf SemiGraphDC}`$ には次の構成素（の集合）があります。

$`{\bf SemiGraphDC}_0`$ ：対象〈0-射〉の集合、対象は半グラフ
$`{\bf SemiGraphDC}_{1v}`$ ：縦1-射〈垂直1-射 | 鉛直1-射〉の集合、縦1-射は半グラフ射
$`{\bf SemiGraphDC}_{1h}`$ ：横1-射〈水平1-射〉の集合、横1-射は半グラフ変形（後述）
$`{\bf SemiGraphDC}_{2}`$ ： 2-射〈二重射〉の集合、2-射は半グラフ2-射（今回は割愛）

既に定義した圏 $`{\bf SemiGraphC}`$ とは次の関係があります。

$`\quad {\bf SemiGraphDC}_0 = \mrm{Obj}({\bf SemiGraphC}) = |{\bf SemiGraphC}|\\
\quad {\bf SemiGraphDC}_{1v} = \mrm{Mor}({\bf SemiGraphC})
`$

二重圏から、$`{\bf SemiGraphDC}_0`$ を対象の集合として、$`{\bf SemiGraphDC}_{1h}`$ を射の集合とする圏を構成できます。これを $`\mrm{H}({\bf SemiGraphDC})`$ または $`{\bf SemiGraphDC}_\mrm{H}`$ と書いて、二重圏 $`{\bf SemiGraphDC}`$ の水平圏〈horizontal category | 横圏〉と呼びます。もとの二重圏が半グラフ二重圏なので、$`\mrm{H}({\bf SemiGraphDC})`$ は半グラフ水平圏〈semi-graph horizontal category〉です。

$`{\bf Gr}`$ は、半グラフ水平圏に（部分圏として）埋め込めます。$`{\bf Graphs}`$ は、半グラフ二重圏に（部分二重圏として）埋め込めます。この記事では埋め込みについては述べませんが。

$`{\bf Gr}`$ や $`{\bf Graphs}`$ では登場しなかった概念として半グラフ二重圏の2-射〈二重射〉があります。これは、半グラフの変形操作のあいだを繋ぐ“高次の射”です。半グラフ二重圏特有の事情として、横1-射を半グラフとみなせるので、2-射を半グラフ射と解釈できます。高次のモノ（2次元の射）の次元を落として捉えること（レイフィケーション）ができます。これは、プログラミングにおいて、プログラムコードもデータだとみなせるのと似た状況です。

半グラフ・プロ射／半グラフ変形

一般に、二重圏の縦1-射を単に射ともいい、横1-射はプロ射〈promorphism | proarrow〉ともいいます。この用語法の習慣により、半グラフ二重圏の横1-射は半グラフ・プロ射〈semi-graph promorphism | promorphism between semi-graphs〉とも呼びます。

$`\alpha, \beta`$ が半グラフ（半グラフ二重圏の対象）のとき、半グラフのあいだの半グラフ・プロ射 $`\phi`$ は次のように書きます。

$`\quad \phi : \alpha \pto \beta \In {\bf SemiGraphDC}`$

矢印 '$`\pto`$' は、縦1-射の矢印 '$`\to`$' と区別するためです。半グラフ変形を表すには、ギリシャ文字アルファベットの $`\phi,\psi`$ などを使います。

では、半グラフ・プロ射とは実際のところ何なのでしょうか？それは、半グラフに対する変形操作です。次のような基本変形操作を組み合わせた変形が半グラフ・プロ射です。

内部辺の切断〈cutting〉：内部辺を切り分けて、2本の外部辺とする。
2つの外部辺の架橋〈bridging〉： 2本の外部辺を繋いで、1本の内部辺とする。切断の逆の操作。
内部辺の縮減〈shrinking〉：内部辺の両端の頂点を1個の頂点にする。当該の内部辺は消去される。
2つの外部辺の縮減〈shrinking〉： 2本の外部辺の2個の端点〈境界頂点〉を1個の頂点にする。当該の2本の外部辺は消去される。

内部辺の縮減を実縮減〈actual shrinking〉、外部辺（2本）の縮減を仮想縮減〈virtual shrinking〉とも呼びます。

グラフ理論では、内部辺の縮減〈実縮減〉を辺の縮約〈edge contraction〉と呼びます。このため、半グラフにおける縮減（実縮減も仮想縮減も）「縮約〈contraction〉」と呼ぶのが普通です。が、縮減を縮約と呼ぶのはかなりミスリーディングです。

幾何的〈位相的〉意味で可縮〈contractible | 縮約可能〉というときの幾何的縮約操作は、サイクルを一点に潰すことはできません。しかし、半グラフの縮減操作は自己ループ辺を潰すことができます。つまり、半グラフ縮減操作は、半グラフの幾何的・ホモトピー的性質を変えてしまうことができます。幾何的〈位相的〉縮約とは違います。また、テンソル計算やトレース付きモノイド圏のストリング図における縮約は、外部辺の架橋〈bridging〉（または架橋した後で縮減）に対応します。架橋と縮減は別な操作です。といった事情で、半グラフに対して「縮約〈contraction〉」は使いません。

切断、架橋、実縮減、仮想縮減を組み合わせた半グラフの変形操作を半グラフ変形〈semi-graph deformation〉と呼びます。半グラフ二重圏のプロ射は半グラフ変形です。以下に、半グラフ変形の例を挙げます。

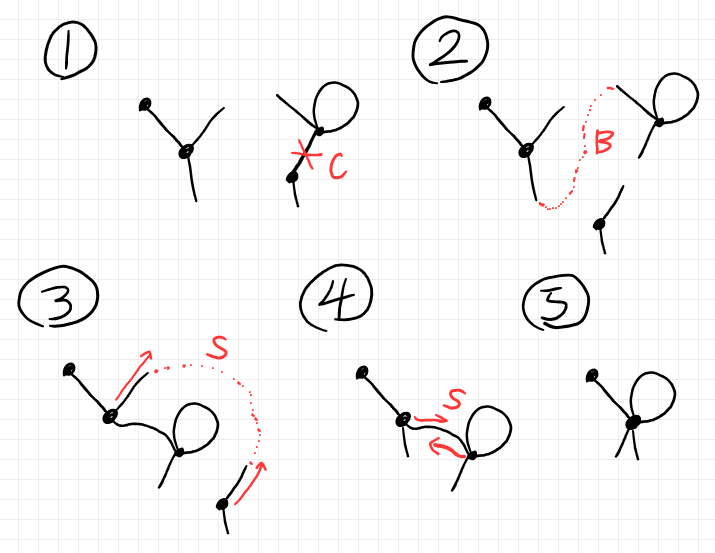
上の図の半グラフ変形は：

'C' とマークされた場所で内部辺を切り分ける（切断）。
'B' とマークされた点線に沿って、2本の外部辺を繋ぐ（架橋）。
2本の外部辺と赤の点線を仮想的な辺と考える（'S' とマークされている）。両端の頂点を一点に縮めて外部辺は消去する（仮想縮減）。
'S' とマークされた内部辺の両端の頂点を一点に縮めて内部辺は消去する（実縮減）。

これらの基本変形を組み合わせると、1番の半グラフは5番の半グラフにまで変形します。

次の状況を考えます。

$`\quad \phi : \alpha \pto \beta \In {\bf SemiGraphDC}\\
\quad \psi : \beta \pto \gamma \In {\bf SemiGraphDC}
`$

つまり、半グラフ $`\alpha`$ が半グラフ変形 $`\phi`$ で半グラフ $`\beta`$ まで変形して、その $`\beta`$ が半グラフ変形 $`\psi`$ で半グラフ $`\gamma`$ まで変形したわけです。$`\phi`$ と $`\psi`$ をこの順で実行した半グラフ変形を $`\phi * \psi`$ と書きます。縦1-射〈半グラフ射〉の結合 '$`;`$' とは区別する必要があるのでアスタリスク記号を使っています。

$`\quad \phi * \psi : \alpha \pto \gamma \In {\bf SemiGraphDC}`$

また、次の状況を考えます。

$`\quad \phi_1 : \alpha_1 \pto \beta_1 \In {\bf SemiGraphDC}\\
\quad \phi_2 : \alpha_2 \pto \beta_2 \In {\bf SemiGraphDC}
`$

半グラフの直和と、それに対応した半グラフ変形の直和を考えることができるので、直和を '$`+`$' で表すと：

$`\quad (\phi_1 + \phi_2) : (\alpha_1 + \alpha_2) \pto (\beta_1 + \beta_2) \In {\bf SemiGraphDC}
`$

「コステロの半グラフ圏から二重関手意味論へ // 半グラフ圏の対称モノイド構造」で述べたように半グラフを対象とする圏には、直和により対称モノイド構造を入れられます。半グラフ二重圏も、対称モノイド二重圏〈symmetric monoidal double category〉の構造を持つのでした。

半グラフ変形を、横結合〈horizontal composition〉'$`*`$' と直和〈direct sum〉$`+`$ で組み合わせてより複雑な半グラフ変形を作り出すことができます。

半グラフ変形の指令半グラフ

前節の半グラフ変形の定義は、操作的・手続き的〈operational/procedural〉でした。半グラフ変形は、入力データである半グラフを受け取って処理を実行して処理結果である半グラフを出力する、という感じです。このような処理の手順は、プログラムコードで記述するのが自然でしょう。半グラフ変形を記述するプログラムコードは、テキストで書くより、それ自体がまた半グラフであるほうが便利です。半グラフ変形のプログラムコードとしての半グラフを、半グラフ変形の指令半グラフ〈instruction semi-graph〉と呼ぶことにします。

指令半グラフは、入力半グラフの処理を施す場所に指令ニモニック〈instruction mnemonic〉（後述）を書き込んだものです。ただし、仮想縮減を施す場所は仮想辺なので、仮想辺を含むような半グラフが必要です。

$`\alpha = (V(\alpha), H(\alpha), \bdry_\alpha, \iota_\alpha)`$ を半グラフとします。半グラフ $`\alpha`$ 上の仮想半グラフ〈virtual semi-graph〉$`(\alpha, G)`$ とは次のものです。

仮想半グラフは、半グラフ $`\alpha`$ と集合 $`G`$ で決まる。
$`G \subseteq \mrm{Pow}_2(T(\alpha))`$

ここで、$`T(\alpha)`$ は半グラフ $`\alpha`$ のテール（外部辺に対応する半辺）の集合です。$`\mrm{Pow}_2(\text{－})`$ は、ちょうど2個の要素を持つ部分集合の集合です。$`a, b\in T(\alpha)`$ だとして、$`\{a, b\} \in G`$ ならば、$`\{a , b\}`$ は、半辺 $`a, b`$ を仮にペアリングした仮想的な内部辺です。もともとは（$`\alpha`$ 内では）、$`\{a\}, \{b\}`$ は2本の外部辺です。

仮想グラフ $`(\alpha, G)`$ において、$`G`$ の要素は仮想辺〈virtual edge〉またはゴースト辺〈ghost edge〉と呼びます。「仮想辺」はボリソフ／マニンの用語、「ゴースト辺」はバーガー／カウフマンの用語です。$`G = \emptyset`$ のとき、仮想グラフ $`(\alpha, G)`$ は通常の半グラフ $`\alpha`$ と同一視します。

[追記]
ボリソフ／マニンとバーガー／カウフマンの用語法だと、後述の指令ニモニック $`\mrm{S}`$（Shrink）が付いた辺（テールのペア）だけを「仮想辺」「ゴースト辺」と呼んでいるようです。指令ニモニック $`\mrm{B}`$（Bridge）を付ける辺（テールのペア）も必要だし、それは実際の辺〈actual edge〉ではないし、困りますね。

上記の定義の仮想辺はそのまま使って、特に指令ニモニック $`\mrm{S}`$（Shrink）が付いた仮想辺をゴースト辺と呼ぶという折衷案にしましょうかね（今後）。
[/追記]

指令ニモニック〈instruction mnemonic〉とは、基本変形操作である Cut, Bridge, Shrink そして何もしないことを表す Nop（No operation）のイニシャル・ラテン文字 'C', 'B', 'S', 'N' からなる集合です。指令ニモニックを単に指令〈instruction〉とも呼びます。指令の集合を次のように書きます。

$`\quad {\bf Instr} := \{\mrm{C}, \mrm{B}, \mrm{S}, \mrm{N}\}`$

指令半グラフ〈instruction semi-graph〉は、仮想半グラフ $`(\alpha, G)`$ の内部辺と仮想辺に指令ニモニックを割り当てたものです。指令ニモニックを割り当てる関数を $`m`$ とすると、$`m`$ は2つの部分 $`m_\mrm{int}, m_\mrm{virt}`$ からなります。

$`\quad m_\mrm{int} : \mrm{Int}E(\alpha) \to \{\mrm{C}, \mrm{S}, \mrm{N}\}\subset {\bf Instr}\:\In {\bf Set}\\
\quad m_\mrm{virt} : G \to \{\mrm{B}, \mrm{S}\}\subset {\bf Instr} \:\In {\bf Set}
`$

$`m_\mrm{int}, m_\mrm{virt}`$ をいちいち区別しないで次のように書きます。

$`\quad m : (\mrm{Int}E(\alpha) + G) \to {\bf Instr} \In {\bf Set}
`$

ただし、内部辺に対する架橋と、仮想辺に対する切断、Nopが禁止されていることは要注意です。

先に上げた半グラフ変形に対する指令半グラフは次のようになります。

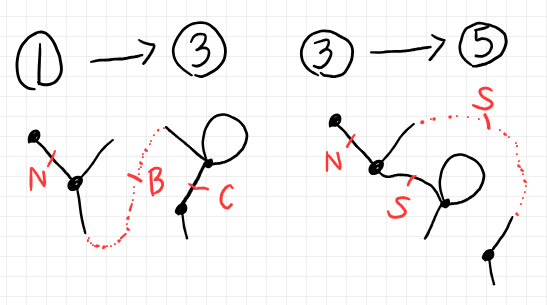
仮想辺の一部とならない外部辺には指令ニモニックは付きません。また、内部辺へのNop（'N'）の割り当ては描くのを省略していいでしょう。よって、実質的な指令ニモニック割り当ては：

仮想辺には必ず指令ニモニック（架橋または縮減）を割り当てる。
切断／縮減の対象となる内部辺には指令ニモニックを割り当てる。

おわりに

大雑把ではありますが、半グラフ二重圏の対象／縦1-射／横1-射〈プロ射〉について説明しました（2-射は説明していません）。今回定義したプロ射である半グラフ変形は、自由度があり過ぎて扱いが難しい面があります。すべての半グラフと半グラフ変形を扱うのではなくて、制限した圏や二重圏を作る必要があります。例えば、コステロの半グラフ二重圏は、半グラフ／半グラフ変形を制限することにより、非常に扱いやすい二重圏になっています。

今回導入した、操作的・手続き的な半グラフ変形と指令半グラフは、ボリソフ／マニンとバーガー／カウフマンの定義に比べると（人によるでしょうが）分かりやすく直感的ではないかと思います。複雑な構造を持つ半グラフ二重圏を調べる道具になると期待できます。

追記：頂点同一視

縮減の指令 $`\mrm{S}`$ が割り当てられた辺（実辺または仮想辺）の両端の頂点は同一視されて一点になります。半グラフ変形では、二頂点のあいだに実辺も仮想辺もなくても同一視が可能です。そのことを、この記事では書き忘れていました。「半グラフ変形とDead-Or-Alive構造 // 頂点同一視関係と頂点マージ変形」に書きました。

*1:$`{\bf semigraph}`$ の反対圏を考えれば、その反対圏上の前層の圏とみなせます。