半グラフのあいだのエタール射

半グラフのあいだの準同型写像（半グラフ変形ではない）がエタールであることを、近傍関手とデカルト四角形〈プルバック図式〉により特徴付けます。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\bdry}{\partial }
\newcommand{\Imp}{\Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
`$

内容：

幾何半グラフと組み合わせ半グラフ
半グラフ射
半グラフのあいだのエタール射
有限バンドルの圏と近傍関手
集合圏のプルバックの特徴付け
ファイバーごとに同型なバンドル射
半グラフのエタール射の特徴付け

幾何半グラフと組み合わせ半グラフ

半グラフに関する記事は、「スケマティック系のハブ記事 // 半グラフ」を基点にたどることができます。

幾何半グラフ〈幾何的半グラフ | geometric semi-graph〉 $`X`$ は、位相空間（位相空間の圏 $`{\bf Top}`$ の対象） $`X_1`$ と、その有限部分集合 $`X_0\subseteq X_1`$ から構成されます。

$`\quad X = (X_0, X_1)\\
\text{Where}\\
\quad X_0, X_1 \in |{\bf Top}|\\
\quad X_0 \subseteq X_1\\
\quad X_0 \text{ is finite}
`$

次の条件が要求されます；位相空間 $`X_1`$ から “$`X_0`$ の要素である有限個の点” を取り除いた位相空間（相対位相を考える） $`X_1 \setminus X_0`$ は、有限個の連結成分を持つ境界無し1次元多様体となる。

連結な境界無し1次元多様体は、開区間（直線と言っても同じ）か円周のどちらかと同型です。よって、上の条件は次のように言っても同じです。

$`X_1 \setminus X_0`$ は、開区間または円周を有限個並べた図形である。

この条件から、$`X_1`$ を構成する材料は次のようになります。

$`n`$ 個の円周（$`X_1\setminus X_0`$ の連結成分）
$`m`$ 個の開区間（$`X_1\setminus X_0`$ の連結成分）
$`k`$ 個の頂点（$`X_0`$ の要素）

$`(n, m, k)`$ は幾何半グラフ $`X`$ を特徴付ける重要な量ですが、それだけで $`X`$ の形が決まるわけではありません。同じ材料からの組み立て方が色々あります。

幾何半グラフ $`X`$ の材料である開区間が、それだけで $`X`$ の連結成分（$`X_1\setminus X_0`$ の連結成分ではない）を構成するとき例外辺〈exceptional edge〉と呼びます。材料である円周は常にそれだけで $`X`$ の連結成分になります。これを例外ループ〈exceptional loop〉と呼びます。

以下の図は、「開放ツリー：半グラフ・ベースのツリー」で使った図で、裸の番号で頂点、括弧囲みの番号で辺を識別しています。

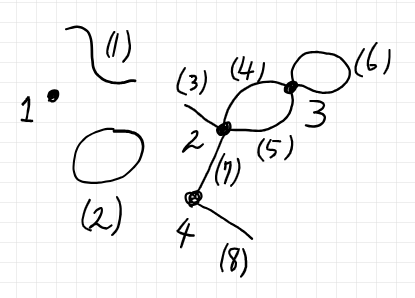
このなかで、(1) が例外辺、(2) が例外ループです。この例では、$`n = 1, m = 7, k = 4`$ です。

幾何半グラフは簡単に定義できますが取り扱いが難しいので、組み合わせ構造として半グラフを定義します。組み合わせ構造としての半グラフを組み合わせ半グラフ〈combinatorial semi-graph〉と呼びます。ここから先に登場するのは組み合わせ半グラフなので、単に「半グラフ」と言えばそれは組み合わせ半グラフです。

半グラフ〈組み合わせ半グラフ〉の定義の仕方により、幾何半グラフの構成素が表現できないことがあります。ボリソフ／マニン〈D. Borisov, Yu. I. Manin〉の半グラフの定義（「半グラフの様々な定義」参照）では、例外辺〈無頂点辺〉も例外ループ〈無頂点ループ〉も表現できません。望月の半グラフの定義（同じ過去記事参照）では例外辺を扱えますが、例外ループは扱えません。「開放ツリー：半グラフ・ベースのツリー」で採用した半グラフの定義では、例外辺を扱えますが、例外ループも自己ループ辺（例外ではない通常ループ）も扱えません。

ここでは、ボリソフ／マニンの定義を採用するので、幾何半グラフのなかで、例外辺も例外ループも持たないものだけを組み合わせ的に扱います。

半グラフ射

半グラフ射は半グラフ変形とは違います（半グラフ変形を「射〈morphism〉」と呼ぶ場合も多いですが）。半グラフ射と半グラフ変形については「半グラフの二重圏と半グラフ変形」に書いています。

半グラフ射について復習すると；半グラフを余前層として定義したときの余前層のあいだの射（つまり自然変換）が半グラフ射〈semi-graph morphism〉です。余前層としての半グラフのソース圏〈域圏〉は次の図式で表現できます。

$`\quad \xymatrix{
% @(inDir, outDir)
F \ar@(ul, dl)[0,0]_{\iota} \ar[r]^{\bdry}
& V
}\\
\quad \iota; \iota = \mrm{id}_F
`$

この図式で表される2対象5射の圏を $`{\bf semigraph}`$ とすると、半グラフのインスタンス $`\alpha`$ は、圏 $`{\bf semigraph}`$ から有限集合圏 $`{\bf FinSet}`$ への関手です。半グラフ射 $`f`$ は次のように書けます。

$`\quad f:\alpha \to \beta \In {\bf SemiGraphC}\\
\Iff f :: \alpha \Rightarrow \beta : {\bf semigraph} \to {\bf FinSet} \In {\bf CAT}\\
\Iff f : \alpha \to \beta \In [{\bf semigraph}, {\bf FinSet}]
`$

半グラフ射は、半グラフ変形と比べると出来ることが少なくなります。内部辺を断ち切って外部辺2本を作ることは出来ないし、外部辺2本を繋げて内部辺を作ることも出来ません。半グラフ射では、外部辺は外部辺に移し、内部辺は内部辺に移すことになります。しかし、頂点マージ（「半グラフ変形とDead-Or-Alive構造〉参照）は許されるので、ループではない内部辺から自己ループ辺を作ることは出来ます。

半グラフの部分半グラフがあるとき、部分半グラフを親〈全体半グラフ〉に埋め込む包含写像は半グラフ射になります。半グラフのフラグの集合に、境界写像／ペアリング対合と協調する同値関係があると、“商半グラフ”を定義できます。もとの半グラフから商半グラフへの標準射影は半グラフ射になります。

半グラフのあいだのエタール射とは、局所的には同型であるような半グラフ射です。「局所的には」とは、「各頂点の近傍では」の意味です。となると、頂点の近傍を定義する必要があります。

半グラフ $`\alpha = (V(\alpha), F(\alpha), \bdry_\alpha, \iota_\alpha)`$ に対して、2種類の近傍を定義します。

$`\text{For }v \in V(\alpha)\\
\quad \mrm{NbF}_\alpha(v) := \{f \in F(\alpha)\mid \bdry_\alpha(f) = v \} \;\in |{\bf FinSet}|\\
\quad \mrm{NbC}_\alpha(v) := (\{v\}, \mrm{NbF}_\alpha(v), \bdry_\alpha|_{\mrm{NbF}_\alpha(v)}, \mrm{id}_{\mrm{NbF}_\alpha(v)})\; \in |{\bf SemiGraphC}|
`$

$`\mrm{NbF}_\alpha(v)`$ を、頂点 $`v`$ の近傍フラグ集合〈set of neighbourhood flags〉、$`\mrm{NbC}_\alpha(v)`$ は近傍カローラ〈neighbourhood corolla〉と呼びます（バーガー／カウフマン〈Clemens Berger, Ralph M. Kaufmann〉の用語では vertex-corolla）。近傍フラグ集合は単なる有限集合ですが、近傍カローラは単一頂点の半グラフです。

半グラフのあいだの射 $`f:\alpha \to \beta \In {\bf SemiGraphC}`$ がエタール〈etale〉であるとは、各頂点ごとに近傍カローラに制限した半グラフ射が同型であることです。頂点 $`v`$ の近傍カローラに制限した半グラフ射 $`f|_v`$ は次のように定義します。

$`f|_v : {\mrm{NbC}_\alpha(v)} \to {\mrm{NbC}_\beta(f_V(v) )} \In {\bf SemiGraphC}\\
\quad (f|_v)_V : \{v\} \to \{f_V(v)\} \text{ only one } \In {\bf FinSet}\\
\quad (f|_v)_F := (f_F)|_{\mrm{NbF}_\alpha(v)}^{\mrm{NbF}_\beta(f_V(v))} : \mrm{NbF}_\alpha(v) \to \mrm{NbF}_\beta(f_V(v)) \In {\bf FinSet}
`$

$`(f|_v)_F`$ は、域も余域も近傍フラグ集合に制限した写像です。

「エタール」という用語の出典として次を挙げられますが、このコック論文が初出というわけではないでしょう。

[Koc20-23]
Title: Whole-grain Petri nets and processes
Author: Joachim Kock
Submitted: 11 May 2020 (v1), 5 Jan 2023 (v4)
Pages: 58p
URL: https://arxiv.org/abs/2005.05108

半グラフ構造を使わなくても、近傍フラグ集合のあいだの写像だけを使ってもエタール射を定義できます。上記の $`(f|_v)_F`$ は、集合 $`{\mrm{NbF}_\alpha(v)}`$ から $`\mrm{NbF}_\beta(f_V(v))`$ への写像です。この写像が同型（つまり双射）であると定義しても同じです。こっちのほうが単純です。

ちなみに、半グラフ $`\alpha`$ に対して、頂点ごとの近傍カローラ達の直和を作ることができます。

$`\quad \sum_{v\in V(\alpha) }\mrm{NbC}_\alpha(v) \;\in |{\bf SemiGraphC}|`$

「開放ツリー：半グラフ・ベースのツリー」で述べたように、バーガー／カウフマンは、近傍カローラ達の直和半グラフを作ることを解剖〈dissection〉と呼んでいます。解剖〈腑分け〉された半グラフは非常に重要です（今はこれ以上述べませんが）。

有限バンドルの圏と近傍関手

ここでの「バンドル」は幾何的なバンドルのことではありません。単なる写像のことです。全射であることも要求しません。

2つの対象と、恒等射でない射をひとつ持つ圏を $`\vec{\bf 2}`$ と書くことにします。便宜上、対象・射に次の名前を付けておきます。

$`\quad \vec{\bf 2} := (1 \overset{\pi}{\to} 0)`$

関手圏 $`[\vec{\bf 2}, {\bf FinSet}]`$ を有限バンドルの圏〈category of finite bundles〉と呼び、 $`{\bf FinBun}`$ と書きます。$`{\bf FinBun}`$ の対象が有限バンドル〈finite bundle〉です。

有限バンドル $`B`$ は関手なので、次の“成分”を持ちます。

有限集合 $`B(1)`$ ：有限バンドルの全集合〈{total | entire} set〉、$`B_1`$ とも書く。
有限集合 $`B(0)`$ ：有限バンドルの底集合〈base set〉、$`B_0`$ とも書く。
写像 $`B(\pi)`$ ：有限バンドルの射影〈projection〉、$`\pi_B`$ とも書く。全射であることを要求しない。

半グラフと記法のルールが変わってしまいます（$`V(\alpha)`$ 方式ではないです）が、有限バンドルは次のように書きます。

$`\quad B = (B_0, B_1, \pi_B)`$

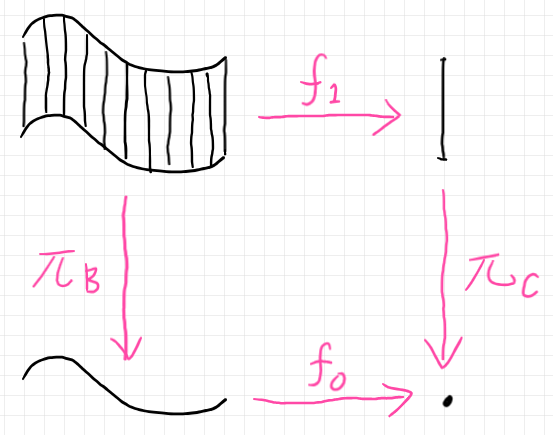
有限バンドル $`B, C`$ のあいだの射は自然変換なので、2つの成分 $`f_0, f_1`$ から構成されます。次の自然性〈naturality〉の条件を満たします。

$`\require{AMScd}
\quad \begin{CD}
B_1 @>{f_1}>> C_1\\
@V{\pi_B}VV @VV{\pi_C}V\\
B_0 @>{f_0}>> C_0\\
\end{CD}\\
\quad \text{commutative in }{\bf FinSet}
`$

有限性の条件をはずすと、一般的なバンドルの圏 $`{\bf Bun}`$ が得られます。

さて次に、半グラフの圏 $`{\bf SemiGraphC}`$ から有限バンドルの圏 $`{\bf FinBun}`$ への関手 $`\mrm{Nb}`$ （Nb は neighbourhood から）を定義します。

対象 $`\alpha \in |{\bf SemiGraphC}|`$ に対する値（有限バンドル）は次のように書けます。

$`\quad \mrm{Nb}(\alpha) :=
\begin{pmatrix}
\sum_{v\in V(\alpha)}\mrm{NbF}_\alpha(v)\\
\downarrow \pi_\alpha\\
V(\alpha)
\end{pmatrix} \;\in |{\bf FinBun}|
`$

$`\mrm{Nb}(\alpha)`$ の底集合は半グラフの頂点集合です。各頂点ごとに、ファイバーとして近傍フラグ集合が生えているバンドル構造になります。なお、有限バンドル $`B`$ に対して、ファイバー〈fiber | fibre〉は次のように定義します。

$`\text{For }b\in B_0\\
\quad (B_1)_b := \{x\in B_1 \mid \pi_B(x) = b\}`$

半グラフ射に対する $`\mrm{Nb}`$ の値の定義と、$`\mrm{Nb}`$ が関手になることの証明は難しくはないので割愛します。こうして構成された関手を近傍関手〈neighbourhood functor〉と呼びます。

有限バンドル $`B`$ があると、底集合の要素 $`b \in B_0`$ ごとに、$`b`$ を単一の頂点としてファイバーをフラグ集合とするカローラ半グラフを作れます。それらカローラ半グラフを直和で寄せ集めるとひとつの半グラフができます。この方法で、有限バンドルの圏から半グラフの圏への関手 $`\mrm{CorollaForest}`$ を構成できます。

関手 $`\mrm{Nb}`$ と $`\mrm{CorollaForest}`$ をこの順で結合すると、半グラフの切り分け分解〈解剖 | dissection〉を行う自己関手になります。

集合圏のプルバックの特徴付け

後で使う都合から、この節で集合圏のプルバックについて調べておきます。

集合圏において、次のようなコスパンを考えます。

$`\quad
\begin{CD}
{} @. B\\
@. @VV{g}V\\
A @>{f}>> X
\end{CD}\\
\quad \In {\bf Set}
`$

このコスパンに対する極限錐〈limit cone〉がプルバック図式〈デカルト四角形 | Cartesian square〉になります。極限対象をプルバックと呼ぶこともあります。また、プルバック〈極限対象〉はファイバー積〈{fibered | fibred | fiber} product〉とも呼びます。集合圏におけるプルバック＝ファイバー積の典型的な構成は次のようになります。

$`\quad P := \{(a, b)\in A\times B\mid f(a) = f(b) \}\\
\quad Q := \sum_{x\in X} f^{-1}(x) \times g^{-1}(x)
`$

$`Q`$ はファイバー（逆像）ごとの積の総和なので、“ファイバー積”という感じがします。$`P`$ は方程式の解集合としての定義です。

ファイバー積は一意的に決まりませんが、どう定義しても同型になります。$`P, Q`$ も同型です。次のような対応が同型を与えます。

$`\quad (a, b) \mapsto (x, (a, b)) \text{ where } x = f(a)\\
\quad (x, (a, b)) \mapsto (a, b)
`$

$`P`$ でも $`Q`$ でも、第一射影と第二射影が自然に定義できるので、ファイバー積と2つの射影を補った次の図式はプルバック図式〈デカルト四角形〉になります（$`Q`$ を $`P`$ にしても同様）。

$`\quad
\begin{CD}
{Q} @>{\pi_2}>> B\\
@V{\pi_1}VV @VV{g}V\\
A @>{f}>> X
\end{CD}\\
\quad \text{commutative}\In {\bf Set}
`$

この図式は、バンドルのあいだの射とみなせます。

$`\quad (f, \pi_2) :
\begin{pmatrix}
Q\\
\downarrow \pi_1\\
A
\end{pmatrix} \to
\begin{pmatrix}
B\\
\downarrow g\\
X
\end{pmatrix} \In {\bf Bun}
`$

バンドルのあいだの射とみなしたプルバック図式は、もちろん特別な性質を持ちます。それは：

ファイバーごとの写像が、すべて同型射〈双射写像〉である。

逆に、ファイバーごとに同型であるバンドル射はプルバック図式を定義します。このことを次節で示します。

ファイバーごとに同型なバンドル射

集合圏での話なので、圏論的な普遍性（極限錐が終対象であること）は使わずに、具体的に構成されたファイバー積に関して要素を使った議論をします。

前節のプルバック図式で、一点 $`x\in X`$ を選ぶと、ファイバーだけを取り上げた次の図式が得られます。（域・余域を制限した写像ともとの写像はオーバーロードします。）

$`\quad
\begin{CD}
f^{-1}(x)\times g^{-1}(x) @>{\pi_2}>> g^{-1}(x)\\
@V{\pi_1}VV @VV{g}V\\
f^{-1}(x) @>{f}>> \{x\}
\end{CD}\\
\quad \text{commutative}\In {\bf Set}
`$

さらに、$`a\in f^{-1}(x)`$ を選んで、$`a`$ 上のファイバーにフォーカスすると次の図式になります。

$`\quad
\begin{CD}
\{a\} \times g^{-1}(x) @>{\pi_2}>> g^{-1}(x)\\
@V{\pi_1}VV @VV{g}V\\
\{a\} @>{f}>> \{x\}
\end{CD}\\
\quad \text{commutative}\In {\bf Set}
`$

この図式は、バンドル射 $`(f, \pi_2)`$ の点 $`a\in A`$ におけるファイバーパート〈fiber part〉を表現しています。そして、この図式の上段は、$`\{a\} \times g^{-1}(x)\cong g^{-1}(x)`$ という同型なので、ファイバーパートは同型です。

以上から、集合圏のプルバック図式〈デカルト四角形〉をバンドル射とみなすと、それはファイバーごとに同型なバンドル射になっていることが分かりました。

今度は逆に、$`f:B \to C \In {\bf Bun}`$ がファイバーごとに同型なバンドル射だとします。$`f`$ を集合圏内に展開すれば：

$`\quad \begin{CD}
B_1 @>{f_1}>> C_1 \\
@V{\pi_B}VV @VV{\pi_C}V \\
B_0 @>{f_0}>> C_0
\end{CD}\\
\quad \text{commutative}\In {\bf Set}
`$

記法を簡略化するために、$`y\in C_0`$ に対して $`X := {f_0}^{-1}(y)`$ と置きます。すると、次の可換図式ができます。

$`\quad \begin{CD}
{\pi_B}^{-1}(X) @>{f_1}>> {\pi_C}^{-1}(y) \\
@V{\pi_B}VV @VV{\pi_C}V \\
X @>{f_0}>> \{y\}
\end{CD}\\
\quad \text{commutative}\In {\bf Set}\\
\quad \text{where }X := {f_0}^{-1}(y)
`$

$`X`$ や $`{\pi_C}^{-1}(y)`$ が空になる可能性がありますが、その場合でも特に問題はありません。

ファイバーごとに同型であることは、次の図式の上段が同型射（双射写像）であることです。

$`\text{For }x\in X\\
\quad \begin{CD}
{\pi_B}^{-1}(x) @>{f_1}>> {\pi_C}^{-1}(y) \\
@V{\pi_B}VV @VV{\pi_C}V \\
\{x\} @>{f_0}>> \{y\}
\end{CD}\\
\quad \text{commutative}\In {\bf Set}
`$

ファイバーごとの同型を寄せ集めると、次の同型が作れます。

$`\quad {\pi_B}^{-1}(X) \cong \sum_{x\in X}{\pi_C}^{-1}(y) \cong X\times {\pi_C}^{-1}(y)`$

よって、先の図式の一部を同型な集合で置き換えて、次の図式が得られます。

$`\quad \begin{CD}
{f_0}^{-1}(y)\times {\pi_C}^{-1}(y) @>{f_1}>> {\pi_C}^{-1}(y) \\
@V{\pi_B}VV @VV{\pi_C}V \\
{f_0}^{-1}(y) @>{f_0}>> \{y\}
\end{CD}\\
\quad \text{commutative}\In {\bf Set}
`$

以上から、ファイバーごとに同型なバンドル射（の図式）は、ファイバー積を定義するデカルト四角形であることが分かりました。ファイバーごとに同型なバンドル射とファイバー積のデカルト四角形は同一視可能です。

半グラフのエタール射の特徴付け

$`f:\alpha \to \beta \In {\bf SemiGraphC}`$ が半グラフのエタール射だとします。これは、$`\alpha`$ の頂点ごとに、その近傍が $`\beta`$ の近傍に同型に移る、ということです。エタール射 $`f`$ を近傍関手により有限バンドルの圏に送ります。

$`\quad \mrm{Nb}(f) :
\begin{pmatrix}
\sum_{v\in V(\alpha)} \mrm{NbF}_\alpha(v) \\
\downarrow \pi_\alpha\\
V(\alpha)
\end{pmatrix} \to
\begin{pmatrix}
\sum_{w\in V(\beta)} \mrm{NbF}_\beta(w) \\
\downarrow \pi_\beta\\
V(\beta)
\end{pmatrix} \In {\bf FinBun}
`$

$`f`$ がエタールであることから、$`\mrm{Nb}(f)`$ はファイバーごとに同型なバンドル射になります。前節の結果から、ファイバーごとに同型なバンドル射は、ファイバー積のデカルト四角形です。

これを利用して、半グラフ射がエタールであることを、次のようにも定義できます。

$`f`$ がエタールであるとは、$`\mrm{Nb}(f)`$ がファイバー積のデカルト四角形〈プルバック図式〉になることである。