半グラフからシステムの記述へ - 檜山正幸のキマイラ飼育記 (はてなBlog)

次の2つの過去記事で半グラフ／型付き半グラフについて述べました。

半グラフ／型付き半グラフの使いみちとして、システムの記述があります。システムは階層的に構成されることがあります。階層的なシステムを記述するには、半グラフも階層化する必要があります。つまり、入れ子の半グラフ〈nested semi-graph〉を導入することになります。

入れ子の半グラフとその応用をうまく定式化するには、けっこう大規模な構造をセットアップする必要があるみたいです。それを一気に述べるのは無理なので、幾つかのサブトピックとだいたいの方針だけをこの記事に記します。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
%\newcommand{\twoto}{\Rightarrow }
\newcommand{\In}{\text{ in } }
%\newcommand{\Imp}{ \Rightarrow }
%\newcommand{\Iff}{\Leftrightarrow }
%\newcommand{\hyp}{\text{－} }
%\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id} }
%\newcommand{\B}{\partial } % boundary
%\newcommand{\mbf}[1]{\mathbf{#1}}
%\newcommand{\pto}{ \supseteq\!\to }
\newcommand{\u}[1]{\underline{#1}}
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Subject}{\Keyword{Subject } }%
\newcommand{\Where}{\Keyword{Where } }
%\newcommand{\Let}{\Keyword{Let } }
`$

内容：

入れ子の型付き半グラフ
型付き半グラフによるシステムの記述
スケマティック圏
インターフェイス付き圏
スケマティック圏とインターフェイス付き圏の実例
SS構成
SS代数、SSクライスリ射
おわりに

[追記]スケマティック圏のよりハッキリした定義を次の記事に書きました。

スケマティック圏：お絵描きできる場所

[/追記]

入れ子の型付き半グラフ

これから型付き半グラフ（「型付き半グラフと指標」参照）を考えますが、型の集合 $`T`$ は固定します。話を簡単にするために、$`T`$ は有限集合とします*1。例えば、

$`\quad T = \{{\bf N}, {\bf R}, {\bf B} \}`$

この例では、$`T`$ は三元集合です。$`T`$ の要素は自然数の集合、実数の集合、ブール値の集合です。$`T`$ は有限集合と仮定してますが、$`T`$ の要素が無限集合なのは別にかまいません。

$`T`$-型付き半グラフ $`(P, B, c, b, w, t)`$ の構造は次の図式で表現されます。

$`\quad \xymatrix{
T & {\bf 1} \ar[d]^{c}
\\
% @(inDir, outDir)
P \ar@(ul, dl)[0,0]_{w}
\ar[u]^{t}
\ar[r]^-{b}
& B
}\\
\quad \text{ in } {\bf FinSet}
`$

$`T`$ を有限集合と仮定したので、図式は有限集合の圏 $`{\bf FinSet}`$ 内の図式となります。追加すべき条件は：

$`w`$ は不動点を持たない対合〈involution〉である。
$`w; t = t`$ である i.e. 型付けはワイヤリングに対して不変である。

型なし半グラフは、$`T = {\bf 1}`$ の場合と考えられるので、次が言えます。

型なし半グラフは特別な型付き半グラフである。

単に「半グラフ」と言ったときでも、常に型が付いている（自明な型かも知れないが）と思ってください。

入れ子の型付き半グラフの一例を挙げましょう。2つの型付き半グラフ $`A, B`$ を考えます。ボックスの集合は次のようだとします。

$`\mrm{Box}(A) = \{A_0, A_1, A_2\}`$ 、$`A_0`$ がキャンバスボックス
$`\mrm{Box}(B) = \{B_0, B_1, B_2\}`$ 、$`B_0`$ がキャンバスボックス

$`A`$ のポートは合計で8個あり、$`B`$ のポートは合計で6個あります。型付け〈typing〉写像の詳細は省略します。型付き半グラフ $`A`$ の内側に型付き半グラフ $`B`$ が入り込んだ入れ子の半グラフ〈nested semi-graph〉を描くと次のようになります。ワイヤーとボックス境界の区別がつきにくかったので、内部ボックスにオレンジ色の影を付けています。

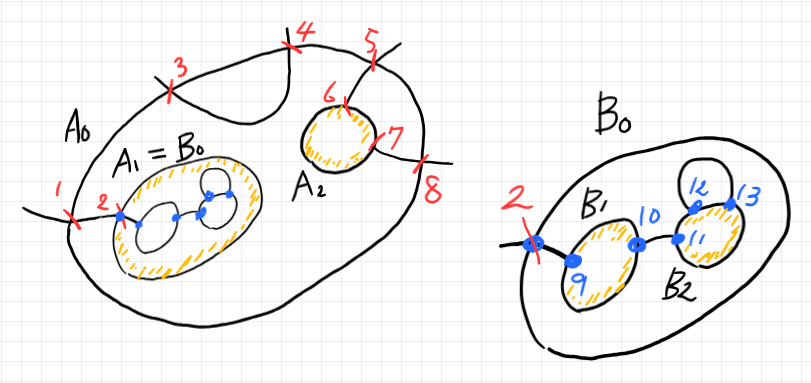
$`A`$ の内部ポート2番は、$`B`$ の唯一の外部ポートと重なります。したがって、入れ子になった後のポートの総数は 8 + 6 - 1 = 13 個になります。それらには、1 から 13 の通し番号を振っています。

入れ子の半グラフがどんなものであるか、この絵を見れば直感的には分かると思います。が、正確な議論を展開するには、絵と目視に頼らない定義が必要になります。

型付き半グラフによるシステムの記述

あるシステムが型付き半グラフで記述できるとき、次のような対応があります。

システム	半グラフ
コンポネント達	内部ボックス達
外部インターフェイス	キャンバスボックスの型付きポート達
内部構造	ワイヤリング
コンポネントのインターフェイス	内部ボックスの型付きポート達

システム（親システム）のコンポネント（子システム）がさらにまた内部構造を持つなら、コンポネントのコンポネント（孫システム）があります。その状況は入れ子の半グラフで表現されます。

コンポネント達をワイヤリングするときや、システムをさらに上位のシステムの一部として埋め込むとき、インターフェイスの整合性がチェックされます。インターフェイスが合致しないと、ワイヤリングや埋め込みはできません。インターフェイスのチェックが出来るためには、当然にシステム／コンポネントに「インターフェイス」の概念が必要です。

型付き半グラフに対しては、そのインターフェイス概念を割と容易に定義できます。準備として、インターフェイスを表す“型付き有限集合の圏”を定義します。型の集合 $`T`$ に対して、$`T`$-型付き有限集合〈$`T`$-typed finite set〉とは、有限集合 $`X`$ とその上の$`T`$-型付け〈$`T`$-typing〉 $`t:X \to T`$ の組 $`(X, t)`$ だと定義します。$`T`$ が了解されていれば、$`T`$-型付き有限集合を単に型付き有限集合〈typed finite set〉といいます。

型付き有限集合は、記号の乱用で次のように書きます。

$`\quad X = (X, t_X) \\
\Where t_X : X \to T \In {\bf FinSet}
`$

$`(X, t_X), (Y, t_Y)`$ が2つの型付き有限集合のとき、写像 $`f:X \to Y`$ が型付き有限集合のあいだの準同型射〈homomorphism〉であるとは、$`f`$ が$`T`$-型付け〈$`T`$-typing〉を保存することです。この条件は、次の図式が可換になることです。

$`\require{AMScd}
\quad \begin{CD}
X @>{f}>> Y\\
@V{t_X}VV @VV{t_Y}V\\
T @= T
\end{CD}\\
\text{commutative in } {\bf FinSet}
`$

$`T`$-型付き有限集合とそのあいだの準同型射の圏を$`T`$-型付き有限集合の圏〈category of $`T`$-typed finite sets〉と呼び、$`{\bf TypedFinSet}[T]`$ と書きます。オーバー圏〈スライス圏〉を使って次のようにも定義できます。

$`\quad {\bf TypedFinSet}[T] := {\bf FinSet}_{/T}`$

型付き半グラフ $`A`$ に対して、ボックスのインターフェイス〈interface of boxes〉は次のように定義します。$`\Subject`$で、定義すべきモノを宣言してから実際の定義を続けます。

$`\For A \in |{\bf TypedSemiGraph}[T]|\\
\Subject \mrm{BIntf}_A : \mrm{Box}(A) \to |{\bf TypedFinSet}[T]|\\
\For x \in \mrm{Box}(A)\\
\Define \mrm{BIntf}_A(x) := ({\mrm{belong}_A}^{-1}(x), \mrm{type}_A|_{{\mrm{belong}_A}^{-1}(x)}) \; \in |{\bf TypedFinSet}[T]|
`$

型付き半グラフ $`A`$ 自体のインターフェイス（外部インターフェイス）は次のように定義します。

$`\For A \in |{\bf TypedSemiGraph}[T]|\\
\Subject \mrm{Intf}(A) \in |{\bf TypedFinSet}[T]|\\
\Define \mrm{Intf}(A) := \mrm{BIntf}_A(\mrm{canvas}_A) \; \in |{\bf TypedFinSet}[T]|
`$

つまり、$`A`$ のインターフェイスは、$`A`$ のキャンバスボックス〈外部ボックス〉のインターフェイスのことです。

インターフェイス概念は、システムでもコンポネントでもコンポネントのコンポネントでも、みんな一律でないといけません。そうでないと、自由に階層的構成ができません。

スケマティック圏

スケマティック圏〈schematic category〉は、特定の圏の固有名ではなくて、圏の種類です。公理的・抽象的に定義したいのですが、現状ではハッキリした完全な公理系は不明です。要求される幾つかの条件は分かってますが（後述）。

[追記]スケマティック圏のよりハッキリした定義を次の記事に書きました。

スケマティック圏：お絵描きできる場所

[/追記]

次の圏達は、スケマティック圏のプロトタイプ的事例です。

$`{\bf FinSet}`$ ：有限集合を対象として、写像を射とする圏。
$`{\bf TypedFinSet}[T]`$ ：前節で述べた、$`T`$-型付き有限集合を対象として、型付けを保存する写像を射とする圏。
$`{\bf PolarFinSet}`$ ：極性付き有限集合を対象として、任意の写像（極性を保存する必要はない*2）を射とする圏（「テンソルの可視化のための半グラフ // 極性付けとワイヤーの向き」参照）。

実際のところ、これら3つの圏と、その組み合わせ・変種で事足りるので、スケマティック圏の一般論が喫緊の課題というわけではないです。

スケマティック圏の動機・用途・目的は、システムの設計図・青写真をそのなかで描ける圏です。スケマティック圏の対象は、システムの素材であるコンポネントのインターフェイスとみなせます。スケマティック圏の射を使って、コンポネント達の繋ぎ合わせ方（How To Wire Them）を指定できます。

"schematic" は、「概要の」「図解の」「図式の」「図式的な」といった意味の形容詞ですが、システムの概要を図解する図式を描く場所がスケマティック圏です。また、"schematic diagram" を単に "schematic" とも呼び、これは回路図の意味です。コンポネント〈素子〉達をワイヤーで繋いだシステム設計図〈青写真〉はまさに回路図です。この“システム設計図〈青写真〉＝回路図”をシステムスキーマ〈system schema〉と呼びます -- 概要は後述、正確な定義はいずれ。

現時点で見当がついているスケマティック圏への要求を述べておきます。圏 $`\cat{I}`$ がスケマティック圏であるためには以下のことが必要です；まず、$`\cat{I}`$ は直和に関して対称モノイド圏になってます。$`\cat{I}`$ は余デカルト・モノイド圏だと言っても同じです。$`(A_i)_{i\in I}`$ が、$`\cat{I}`$ の有限個の対象の族だとすると、この族の余極限（のひとつ）は総直和で与えられます。

$`\quad \mrm{colim}_{i\in I}A_i = \sum_{i\in I}A_i \In \cat{I}`$

スケマティック圏 $`\cat{I}`$ の対象の集合には、厳密に対合的な写像があります。

$`\quad N:|\cat{I}| \to |\cat{I}| \In {\bf SET}\\
\Where N ; N = \id_{|\cat{I}|}
`$

さらに $`N`$ は次を満たします。$`O`$ は直和の単位対象だとします。

$`\quad N(O) = O\\
\For A, B \in |\cat{I}|\\
\quad N(A + B) = N(A) + N(B)
`$

この写像 $`N`$ を否定〈negation〉と呼んでおきます。圏 $`{\bf PolarFinSet}`$ の場合なら、極性を反転させた極性付き有限集合を $`N(A)`$ とします。否定は恒等写像でもかまいません。$`{\bf FinSet}, {\bf TypedFinSet}[T]`$ の否定は恒等写像です。

スケマティック圏 $`\cat{I}`$ には、ワイヤリング射〈wiring morphism〉と呼ばれ射のクラス $`W \subseteq \mrm{Mor}(\cat{I})`$ が指定されています。ワイヤリング射（$`W`$ の要素）がコンポネント達のワイヤリング（相互接続）に使われます。$`W`$ の公理的特徴付けがイマイチ分からないのですが、次は要求されるでしょう。

$`w \in W`$ ならば、$`w`$ は自己射〈endomorphism〉である。
$`w, w' \in W`$ ならば、$`w + w' \in W`$ 。
（他にもあるだろう）

スケマティック圏を使っていくうちに、$`W`$ の特徴付けもハッキリしてくるでしょう。

スケマティック圏がうまく公理化できたとしても、公理は満たすが正体不明なスケマティック圏を使う機会はないと思うので、有限集合の圏 $`{\bf FinSet}`$ への忘却関手〈忠実関手〉を持つ圏に限定してもいいかも知れません。

まだ不明瞭な概念ではありますが、スケマティック圏達の圏が存在することを仮定してそれを $`{\bf SchemCAT}`$ とします。$`\cat{I}\in |{\bf SchemCAT}|`$ は、$`\cat{I}`$ がスケマティック圏であることを意味します。

インターフェイス付き圏

圏 $`\cat{C}`$ があるとします。インフォーマルな想定（気持ち）として、圏 $`\cat{C}`$ の対象はシステムを構成するためのコンポネントだとします。$`\cat{C}`$ の対象＝コンポネントはブラックボックスで、中身は見えないとします。しかし、明白なインターフェイスを持っているとします。

以上の状況を定式化するために、インターフェイス付き圏〈category with interface〉という概念を使います。インターフェイス付き圏は、次の3つの構成素（1つの関手とも言えますが）からなります。

圏 $`\cat{C}`$
スケマティック圏 $`\cat{I}`$
関手 $`\mrm{Intf} : \cat{C}\to \cat{I}`$

圏 $`\cat{C}`$ や関手 $`\mrm{Intf}`$ には特に条件を付けません。例えば、$`\cat{C}`$ が離散圏（事実上は集合）であってもかまいません。スケマティック圏 $`\cat{I}`$ は単なる圏ではなくて色々な構造を持つので、$`\mrm{Intf}`$ の定義時にはそれらの構造を忘れる必要があります。スケマティック圏 $`\cat{I}`$ の台圏〈underlying category〉を $`\u{\cat{I}}`$ として、関手 $`\mrm{Intf}`$ の正確な記述は次のようです。

$`\quad \mrm{Intf} : \cat{C}\to \u{\cat{I}} \In {\bf CAT}`$

関手 $`\mrm{Intf}`$ がコンポネント（$`\cat{C}`$ の対象）のインターフェイスを与えます。コンポネントのあいだの射にはインターフェイスのあいだの射が対応します。

スケマティック圏 $`\cat{I}`$ は固定するとして、いつもの記号の乱用で次のように書きます。

$`\quad \cat{C} = (\cat{C}, \mrm{Intf}_\cat{C})`$

インターフェイス圏という構造のなかの構成素役割り名として次の呼び名を使います。

圏 $`\cat{C}`$ ： コンポネントの圏〈category of components〉
スケマティック圏 $`\cat{I}`$ ： インターフェイスの圏〈category of interfaces〉
関手 $`\mrm{Intf} : \cat{C}\to \cat{I}`$ ： インターフェイス関手〈interface functor〉

$`\cat{C}`$ と $`\cat{D}`$ が2つのインターフェイス付き圏のとき、そのあいだの準同型射〈homomorphism〉 $`F`$ は、次の図式を（厳密に）可換にする関手です。

$`\quad \begin{CD}
\cat{C} @>{F}>> \cat{D}\\
@V{\mrm{Intf}_\cat{C}}VV @VV{\mrm{Intf}_\cat{D}}V\\
\u{\cat{I}} @= \u{\cat{I}}
\end{CD}\\
\quad \text{commutative in }{\bf CAT}
`$

もっとゆるい準同型射の定義のほうが実用的かも知れませんが、今回はこの定義を採用します。

スケマティック圏 $`\cat{I}`$ をインターフェイスの圏とするインターフェイス付き圏を対象として、準同型射を射とする圏をインターフェイス付き圏の圏〈category of categories with interface〉と呼び、$`{\bf IntfCAT}[\cat{I}]`$ と書きます。$`{\bf IntfCAT}[\cat{I}]`$ に2-射は考えずに1-圏だとします。$`{\bf IntfCAT}[\cat{I}]`$ はとても大きい圏〈very large category〉達の2-圏の対象になっています。

$`\quad {\bf IntfCAT}[\cat{I}] \in |\mathbb{CAT}|`$

圏 $`{\bf IntfCAT}[\cat{I}]`$ のなかで、コンポネントからシステムを構成する作業を行います。$`{\bf IntfCAT}[\cat{I}]`$ が複雑で大きすぎると感じたら、構造を簡略化したりサイズを小さくしたりしてかまいません。例えば次のような圏で代替します。

$`{\bf IntfCat}[\cat{I}]`$ ：インターフェイス付きの小さい圏を対象とする圏
$`{\bf IntfSET}[\cat{I}]`$ ：インターフェイス付きの（小さくないかも知れない）集合を対象とする圏
$`{\bf IntfSet}[\cat{I}]`$ ：インターフェイス付きの小さい集合を対象とする圏

スケマティック圏とインターフェイス付き圏の実例

スケマティック圏の実例として $`{\bf PolarFinSet}`$ を取り上げます。この圏の対象は、有限集合 $`X`$ とその上の極性付け $`p_X : X \to \{+, -\}`$ の組 $`(X, p_X)`$ です（若干記号の乱用）。射は、台集合のあいだの任意の写像で、極性を保存する必要はありません。

スケマティック圏は単なる圏ではなくて、次の構造を要求されます。

余デカルト・モノイド構造
否定
ワイヤリング射の族

$`{\bf PolarFinSet}`$ の余デカルト・モノイド構造は簡単に定義できます。$`(X, p_X)`$ と $`(Y, p_Y)`$ の直和は次のようです。

$`\quad (X, p_X) + (Y, p_Y) := (X + Y, [p_X, p_Y])`$

ここで $`[p_X, p_Y]`$ は、写像のコペアです。直和の単位対象 $`O`$ は：

$`\quad O := (\emptyset, \theta_T)`$

ここで $`\theta_T`$ は、空集合からの唯一の写像です。

$`{\bf PolarFinSet}`$ の否定の定義のために、極性の否定 $`\mrm{neg}`$ を定義します。$`\Subject`$で、定義すべきモノを宣言してから実際の定義を続けます。

$`\Subject \mrm{neg} : \{+, -\} \to \{+, -\} \In {\bf FinSet}\\
\Define \mrm{neg} := (+ \mapsto -,\; - \mapsto +)
`$

$`{\bf PolarFinSet}`$ の否定は次のように定義します。

$`\Subject N : |{\bf PolarFinSet}|\to |{\bf PolarFinSet}| \In {\bf SET}\\
\For (X, p_X) \in |{\bf PolarFinSet}|\\
\Define N( (X,p_X) ) := (X, p_X;\mrm{neg}) \;\in |{\bf PolarFinSet}|
`$

これが否定の条件（前々節）を満たすのは明らかでしょう。

最後に、ワイヤリング射の族 $`W \subseteq \mrm{Mor}({\bf PolarFinSet})`$ を定義します。ワイヤリング射は自己射〈endomorphism〉ですが、$`w: (X,p_X) \to (X,p_X)`$ がワイヤリング射であるための条件を次のように決めます。

写像として対合〈involution〉である。つまり、$`w;w = \id_X`$ 。
写像として不動点を持たない。つまり、$`\forall x\in X.\, w(x) \ne x`$ 。
極性を反転する。つまり、$`\forall x\in X.\, p_X(w(x)) = \mrm{neg}(p_X(x))`$

$`X`$ の要素の二元集合 $`\{x, w(x)\}`$ をワイヤーと考えることができます。ワイヤーの両端の極性は異なるので、例えば「マイナスからプラスへ」としてワイヤーの向きを決めることができます。

スケマティック圏の構造が載った $`{\bf PolarFinSet}`$ を、構成素を列挙して書くなら：

$`\quad ({\bf PolarFinSet}, +, O, \alpha, \lambda, \rho, \sigma, N, W)`$

これは長いので、適宜、記号の乱用と省略を使います。

さて、$`\cat{I}`$ をスケマティック圏（例えば $`{\bf PolarFinSet}`$）として、$`\cat{I}`$ をインターフェイスの圏とするインターフェイス付き圏の例を挙げましょう。$`\cat{I}`$ のスケマティック構造（スケマティック圏としての追加構造）を捨てて単なる圏とみなしたもの（台圏）は $`\u{\cat{I}}`$ と書きます。

自明な、しかし重要なインターフェイス付き圏は次です。

$`\quad \mrm{Id}_{\u{\cat{I}}} : \u{\cat{I}} \to \u{\cat{I}} \In {\bf CAT}`$

つまり、コンポネントの圏を $`\u{\cat{I}}`$ として、インターフェイス関手を恒等関手と置いたものです。コンポネントがインターフェイスなので、中身がないのですが、インターフェイスのみの計算はこのセッティングで行います。

$`\cat{D}`$ は $`\u{\cat{I}}`$ の部分圏とします。次もインターフェイス付き圏になります。

$`\quad \mrm{Incl}_{\cat{D}} : \cat{D}\to \u{\cat{I}} \In {\bf CAT}`$

ここで $`\mrm{Incl}_{\cat{D}}`$ は、部分圏の包含関手です。これも中身がないセッティングです。

$`A`$ は集合（大きい集合を許す）とします。次の写像を考えます。

$`\quad F: A \to |\cat{I}| \In {\bf SET}`$

$`A`$ を離散圏とみなして、$`F`$ は離散圏からの関手とみなせます。集合・写像の圏・関手化も同じ記号を使いますが、次のインターフェイス付き圏ができます。

$`\quad F: A \to \u{\cat{I}} \In {\bf CAT}`$

コンポネントの圏が、事実上は集合（小さくないかも知れない）の例ですが、このような例は扱いやすいのでよく出現します。

もっと中身がある事例は、次の機会に述べます。

SS構成

SSはシステムスキーマ〈System Schema〉のことです。与えられた$`\cat{I}`$-インターフェイス付き圏 $`\cat{C}`$ から、システムスキーマを対象とする圏 $`\mrm{SS}(\cat{C})`$ を構成できます。$`\mrm{SS}(\cat{C})`$ には$`\cat{I}`$-インターフェイス付き圏の構造が入ります。また、構成は関手性〈functoriality〉を持ちます。つまり、$`\mrm{SS}`$ は次のような自己関手になります。

$`\quad \mrm{SS} : {\bf IntfCAT}[\cat{I}] \to {\bf IntfCAT}[\cat{I}] \In \mathbb{CAT}`$

さらには、$`\mrm{SS}`$ を台関手にするモナドに仕立てたい、という目論見です。

まずは地道に $`\mrm{SS}`$ を定義する必要があります。$`\mrm{SS}`$ のベースとなるのは、以下の過去記事で述べたファミリー構成 $`\mrm{Fam}`$ です。

圏 $`\cat{D}`$ に対して、$`I`$ をインデックス集合とする$`\cat{D}`$-ファミリー〈$`\cat{D}`$-family〉とは次の形の写像です。

$`\quad F:I \to |\cat{D}| \In {\bf SET}\:\text{ for some }I\in |{\bf Set}|
`$

ここでは、インデックス集合を有限集合に限定したファミリーだけを考えます。

$`\quad F:I \to |\cat{D}| \In {\bf SET}\:\text{ for some }I\in |{\bf FinSet}|
`$

その他は、通常のファミリー構成とまったく同じに定義すると、次の関手が作れます。

$`\quad \mrm{Fam}^{\bf Fin} : {\bf CAT}^1 \to {\bf CAT}^1 \In \mathbb{CAT}`$

ここで $`{\bf CAT}^1 = {\bf CAT}\!\updownarrow^{1}`$ は、2-射〈自然変換〉を捨てた圏達の1-圏です。

$`\mrm{Fam}^{\bf Fin}(\cat{D})`$ の対象は $`(I, F)`$ のように書きます。射は $`(\varphi, \alpha)`$ のように書きます（「ファミリー構成モナド：大規模構造の事例として」参照）。

$`\cat{C}`$ を$`\cat{I}`$-インターフェイス付き圏だとします。記号の乱用をすると混乱しそうなので、次の記法を採用します。

$`\quad \cat{C} = (\u{\cat{C}}, \mrm{Intf}_\cat{C})\\
\Where\\
\quad \u{\cat{C}} \in |{\bf CAT}|\\
\quad \mrm{Intf}_\cat{C} :\u{\cat{C}} \to \u{\cat{I}} \In {\bf CAT}
`$

$`\u{\cat{C}}`$ はインターフェイス付き圏 $`\cat{C}`$ の台圏です。

インターフェイス付き圏 $`\cat{C}`$ のシステムスキーマは、$`\u{\cat{C}}`$-ファミリーに構成素を追加したもので、次のように書けます。

$`\quad (I, F, o, w)`$

$`(I, F)`$ は$`\u{\cat{C}}`$-ファミリーで、追加の構成素は：

外部インターフェイス〈outer interface〉： $`o \in |\cat{I}|`$
ワイヤリング〈wiring〉： $`w \in W \subseteq \mrm{Mor}(\cat{I})`$

$`w`$ はインターフェイスの圏 $`\cat{I}`$ のワイヤリング射ですが、その域かつ余域は：

$`\quad o + \sum_{i\in I}\mrm{Intf}_\cat{C}(F(i)) \;\in |\cat{I}|`$

このような $`(I, F, o, w)`$ が $`\mrm{SS}(\cat{C})`$ の対象です。$`\mrm{SS}(\cat{C})`$ の射については今日は割愛します。$`\mrm{SS}(\cat{C})`$ が再びインターフェイス付き圏となるには、$`\mrm{Intf}_{\mrm{SS}(\cat{C})}`$ が必要ですが、対象に対しては次の簡単な定義でインターフェイスが与えられます。

$`\quad |\mrm{SS}(\cat{C})| \ni (I, F, o, w) \mapsto N(o) \in |\cat{I}|`$

否定を取っているのはテクニカルな都合からです。

SS代数、SSクライスリ射

$`\mrm{SS}`$ が圏 $`{\bf IntfCAT}[\cat{I}]`$ 上のモナドになること（モナド乗法・単位を定義可能なこと）は示していませんが、もしモナドになってくれると、色々とうれしいことがあります。

モナドがあればそのアイレンベルク／ムーア代数を作れます。SSモナドのアイレンベルク／ムーア代数は次の形をしています。

$`\quad \Phi: \mrm{SS}(\cat{C}) \to \cat{C} \In {\bf IntfCAT}[\cat{I}]`$

$`\Phi`$ はアイレンベルク／ムーア代数の演算を与える関手ですが、システムスキーマ $`S`$ に、$`\cat{C}`$ の対象 $`\Phi(S) \in |\cat{C}|`$ を対応させます。これは、設計図／青写真である $`S`$ にその実装〈implementation〉 $`\Phi(S)`$ を対応させているとみなせます。つまり、SSモナドのアイレンベルク／ムーア代数は、コンポネント指向／インターフェイス指向のソフトウェアの世界の圏論的定式化になっています。

モナドに付随するもうひとつの概念であるクライスリ射を考えてみます。SSモナドのクライスリ射は次の形をしています。

$`\quad P : \cat{C} \to \mrm{SS}(\cat{C'}) \In {\bf IntfCAT}[\cat{I}]`$

これは、$`\cat{C}`$ の対象に、$`\cat{C'}`$ 上のシステムスキーマを割り当てています。これは代入〈substitution〉や手続き〈procedure〉の定式化になっています。クライスリ射を集めたクライスリ圏は、代入計算／手続きの合成計算／テンプレート計算の計算系になります。

ここで特筆すべきは、共通インターフェイスの圏である $`\cat{I}`$ はスケマティック圏であるため、システムスキーマやその操作には、半グラフなどによる図示・視覚化が対応していることです。諸々のことを、文字通り「目に見える」形で表現できるのです。

おわりに

最後は急ぎ足で概略だけですが、冒頭に書いたように「一気に述べるのは無理」なので、続きはおいおいぼちぼち書くでしょう。一般論の続きより先に、データベースやテンソル計算への応用を述べるかも知れません。いずれにしても、スケマティック圏とSS構成は色々と使えそうです。

[追記]スケマティック圏のよりハッキリした定義を次の記事に書きました。

スケマティック圏：お絵描きできる場所

[/追記]

*1:実用上は、有限集合で十分だと思います。

*2:通常の用途では極性を保存すべきでしょうが、ワイヤリングの用途では極性を保存できません。