昨日の記事「ダンジョン圏における確率伝搬法」に出てきたダンジョン圏〈dungeon category〉は、最近はハイパーグラフ圏〈hypergraph category〉と呼ぶことが多いようです。(個人的には「ダンジョン圏」の語感が好きですが。)
ハイパーグラフ圏のまとまった解説は、フォング/スピヴァックの次の論文です。
- Title: Hypergraph Categories [21 Jun 2018 (v1), 18 Jan 2019 (v3)]
- Authors: Brendan Fong, David I Spivak
- Pages: 38p
- URL: https://arxiv.org/abs/1806.08304
冒頭を読んでみましたが、長めだし難しそうだしで、読むのやめました(へたれ)。
フォングの学位論文の第1章がハイパーグラフ圏の説明になっています。
- Title: The Algebra of Open and Interconnected Systems [17 Sep 2016]
- Author: Brendan Fong
- Pages: 230p
- URL: https://arxiv.org/abs/1609.05382
第1章は20ページ(p.19 -- p.38)です。第1章の前半はモノイド圏の復習、後半は一貫性の証明と実例で、p.27 -- p.31 の5ページにハイパーグラフ圏の定義と重要な性質が書いてあります。ここだけ読もう、と(へたれ)。
内容:
ハイパーグラフ圏の同義語
この5ページと、フォング/スピヴァックの冒頭の情報から; ハイパーグラフ圏は何度も(少なくとも5回は)独立に再発見され、次のような呼び名があるそうです。
- well-supported compact closed category (Carboni, Walters)
- dgs-monoidal category (Gadducci, Heckel)
- dungeon category (Morton)
最初の発見は1991年、カルボーニ/ウォルターズ(Aurelio Carboni, R.F.C. Walters)によるらしいです。
ハイパーグラフ圏という名称を与えたのは、キッシンジャー(Aleks Kissinger 2014)とフォング(Brendan Fong 2015)で、この二人はたぶん(少なくとも名称に関しては)申し合わせていたのでしょう。モートンのダンジョン圏も同時期(2014)で、キッシンジャー/フォングとは独立です。
フォング学位論文のp.30に、ハイパーグラフ圏と名付けた理由は、そのテの圏の射は有向ハイパーグラフの辺〈有向ハイパー辺 | ハイパーアロー〉で図示できるからだ、と書いてあります。(下はp.30のハイパーアローの絵。)
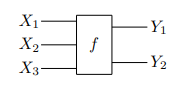
いやいやいや、単なるモノイド圏の射でもハイパーアローで図示するでしょ。その理由は説得力ないなー。有向じゃなくて無向ハイパーグラフを引き合いに出したほうがいいと思いますね。ハイパーグラフ圏は、無向ハイパーグラフの無向ハイパー辺〈undirected hyperedge〉に解釈を与えることができる、と。
ひとつの無向ハイパー辺に対して、ハイパーグラフ圏の複数の射が対応します。それらの射達は、再配置オペレーター〈reshaping operator〉で相互に変換可能です。再配置オペレーターはモートンが使っている概念で、フォングは言及してませんが、射の再配置〈reshape | reshaping〉は便利な道具だと思います。
ハイパーグラフ圏の定義
モートンによるダンジョン圏と、フォングによるハイパーグラフ圏は、(本質的な違いはないにしろ)表面上は違う定義を採用しています。フォングのハイパーグラフ圏のほうが、整理され洗練されている印象があります。
モートンのダンジョン圏〈dungeon category〉Cの定義は次のようです。
- Cは、コンパクト圏*1である。
- Cは、特殊可換フロベニウス代数モダリティを備えている。
- Cは、スパイダー一貫性を持つ(スパイダー射からなる部分圏 Spid(C) はやせている)。
一方、フォングのハイパーグラフ圏では、コンパクト構造は仮定されず、後から導入されます。スパイダー一貫性も仮定〈公理〉ではなくて、後から証明される定理(後述スパイダー定理)です。ハイパーグラフ圏〈hypergraph category〉Cの公理とは:
- Cは、対称モノイド圏である。
- Cは、特殊可換フロベニウス代数モダリティを備えている。
特殊可換フロベニウス代数モダリティ〈special commutative Frobenius {algebra | monoid} modality〉*2とは、Cの対称Xごとに、Xを台対象とする特殊可換フロベニウス代数〈特殊可換フロベニウス・モノイド〉と呼ばれる代数構造 (X, μX, δX, ηX, εX) の割り当てのことです。Cのモノイド構造との整合性が必要です、それは次の図で表現できます(フォング学位論文 p.29)。
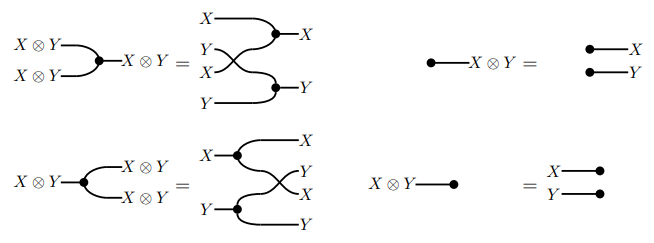
特殊可換フロベニウス代数を構成するCの射は、フロベニウス射〈Frobenius morphism〉と呼びます。モートンの意味のスパイダー射〈spider morphism〉は、恒等/対称/フロベニウス射から構成される射です。[追記]モノイド圏の構造射である結合律子〈associator〉、左単位律子〈left unitor〉、右単位律子〈right unitor〉も入りますね。モートンは厳密モノイド圏(一般のモノイド圏を厳密化した後)を想定していたような気がします。[/追記]
すべてのスパイダー射からなる部分圏がやせているという事実は、正規化定理/一貫性定理の形で述べられます。それをスパイダー定理〈spider theorem〉と呼ぶようです。
「スパイダー/スパイダー定理」という言葉は、2014年より以前からあったようで、2009年投稿の次の論文の第7章は "Phase shifts and a generalised spider theorem" です*3。
- Title: Interacting Quantum Observables: Categorical Algebra and Diagrammatics [25 Jun 2009 (v1), 21 Apr 2011 (v3)]
- Authors: Bob Coecke, Ross Duncan
- Pages: 81p
- URL: https://arxiv.org/abs/0906.4725
ここまでの話をまとめると、ダンジョン圏の公理に含まれるコンパクト性*4とスパイダー一貫性は、実は定理になるということです。ハイパーグラフ圏(本質的にダンジョン圏と同義)は、対称モノイド圏と特殊可換フロベニウス代数モダリティだけで定義されます。
ハイパーグラフ圏のフロベニウス射は、対象でインデックスされた射の族ですが、自然変換であることは要求しません。非自然な構造なのです。これは、扱いにくい面も生じますが、利便性もあります。非自然な構造の利用は増えるのではないかと思います。