コステロの半グラフ圏から二重関手意味論へ

直前の記事「コステロの半グラフ圏によるシステム記述」で使用したコステロの半グラフ圏はホントに使い勝手が良いです。半グラフ圏の部分圏をとったり、半グラフ圏の変種を考えることにより、色々な応用ができます。しかし、その定義にやや曖昧なところもあるので、この記事である程度ハッキリさせて、圏類似代数系の意味論への応用を探ります。$`\newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\In}{\text{ in } }
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{FProd}[3]{ \mathop{\underset{#2} {_{#1} {\times}_{#3} }} }
\newcommand{\dimU}[2]{{#1}\!\updownarrow^{#2}}`$

内容：

半グラフ、植物、林

「亜群をベースとする圏類似構造： コステロの事例」から、半グラフ $`\alpha`$ の構成素と半グラフから容易に構成できる集合・写像を再掲します。

• $`V(\alpha)`$ ： $`\alpha`$ の頂点の集合
• $`H(\alpha)`$ ： $`\alpha`$ の半辺の集合
• $`\pi_\alpha: H(\alpha) \to V(\alpha)`$ ： $`\alpha`$ の半辺の境界写像
• $`\sigma_\alpha : H(\alpha) \to H(\alpha)`$ ： $`\alpha`$ の半辺のパートナー指定対合
• $`T(\alpha)`$ ： $`\alpha`$ のテール（外部辺と一対一対応）の集合
• $`E(\alpha)`$ ： $`\alpha`$ の辺の集合
• $`C(\alpha)`$ ： $`\alpha`$ の連結成分の集合
• $`\rho_\alpha : T(\alpha) \to C(\alpha)`$ ： $`\alpha`$ のテールに、そのテールが所属する連結成分を対応させる写像

辺の集合 $`E(\alpha)`$ は、半辺の集合 $`H(\alpha)`$ を「$`\sigma_\alpha`$ で移りあえる」という同値関係で割った商集合です。$`\pi = \pi_\alpha`$ を既に使ってしまっているので、商集合への標準射影は次のように書きます。

$`\quad \mrm{edge}_\alpha : H(\alpha) \to E(\alpha) \In {\bf FinSet}`$

過去の記事（「亜群をベースとする圏類似構造： コステロの事例」と「コステロの半グラフ圏によるシステム記述」）では、テールと外部辺を適宜同一視していました。ここでは、区別して定義します。

$`\quad T(\alpha) := \{h\in H(\alpha) \mid \sigma_\alpha(h) = h \}\\
\quad \mrm{Ext}E(\alpha) := \{e\in E(\alpha) \mid \exists t\in T(\alpha).\, \mrm{edge}_\alpha(t) = e \}\\
\quad \mrm{Int}E(\alpha) := E(\alpha) \setminus \mrm{Ext}E(\alpha)
`$

この定義から、$`T(\alpha)`$ と $`\mrm{Ext}E(\alpha)`$ は別の集合ですが、規準的〈canonical〉に $`T(\alpha) \cong \mrm{Ext}E(\alpha)`$ です。任意の辺は、外部辺（$`\mrm{Ext}E(\alpha)`$ の要素）か内部辺（$`\mrm{Int}E(\alpha)`$ の要素）のどちらかに分類されます。

グラフに関連して、木〈ツリー〉、根〈ルート〉、葉〈リーフ〉などの言葉が使われるので、悪乗りして、連結な半グラフを植物〈plant〉と呼ぶことにします。実は、「バエズ／ドーラン植物」で「植物」は使っています。

空集合の連結性は物議をかもす話題です（empty space, connectedness）が、空な半グラフを植物に入れても入れなくても、林の概念により調整できるので、まーどっちでもいいです。

林〈forest〉とは、植物（連結な半グラフ）のインデックス付き族〈indexed family of plants〉です。インデキシング集合を $`I`$ として、林は $`(P(i))_{i\in I}`$ と書けます。任意の半グラフは連結成分に分解できるので、連結成分の集合 $`C(\alpha)`$ が規準的〈canonical〉なインデキシング集合となります。

過去の記事では、半グラフ $`\alpha`$ の連結成分の集合 $`C(\alpha)`$ の要素と、対応する部分半グラフをあまり区別しませんでしたが、$`c\in C(\alpha)`$ に対応する部分半グラフ（植物になる）を $`P_\alpha(c)`$ とします。部分半グラフであることを、包含の記号 '$`\subseteq`$' で書くなら：

$`\quad P_\alpha(c) \subseteq \alpha \text{ for }c \in C(\alpha)`$

半グラフ圏の対称モノイド構造

半グラフの直和は、有限集合の直和／写像の直和を使って容易に定義できます。念の為に定義を書いておくと：

• $`V(\alpha + \beta) := V(\alpha) + V(\beta) \;\in |{\bf FinSet}|`$
• $`H(\alpha + \beta) := H(\alpha) + H(\beta) \;\in |{\bf FinSet}|`$
• $`\pi_{\alpha + \beta} := \pi_\alpha + \pi_\beta \;: H(\alpha + \beta) \to V(\alpha + \beta)\In {\bf FinSet}`$
• $`\sigma_{\alpha + \beta} := \sigma_\alpha + \sigma_\beta \;: H(\alpha + \beta) \to H(\alpha+\beta)\In {\bf FinSet}`$

空な半グラフが直和に対する単位対象になります。

（コステロの）半グラフ圏 $`{\bf CSemiGraph}`$ は、対象も射も半グラフでした。上記で定義した半グラフの直和を対象にも射にも適用すると、$`{\bf CSemiGraph}`$ は対称モノイド圏になります。「亜群をベースとする圏類似構造： コステロの事例」で述べたように、$`{\bf CSemiGraph}`$ が通常の圏かどうかは怪しいので、その上に対称モノイド構造を載せた“対称モノイド圏”も怪しいのですが、その点についてはまた後で触れます。

対称モノイド構造を備えた $`{\bf CSemiGraph}`$ を $`({\bf CSemiGraph}, +, {\bf 0})`$ と書きます。$`{\bf 0}`$ は空な半グラフです。

半グラフのアルファ変換亜群

半グラフ圏 $`{\bf CSemiGraph}`$ の対象はカローラ林〈corolla forest〉で、射は一般の（任意の）半グラフでした。これとは別に、対象が任意の半グラフで、射が半グラフの構造を保つ写像であるような圏を考えます。

2つの半グラフ $`\alpha, \beta`$ のあいだの準同型写像〈homomorphism〉は、次のような2つの写像の組です。

$`\quad f_V : V(\alpha) \to V(\beta) \In {\bf FinSet}\\
\quad f_H : H(\alpha) \to H(\beta) \In {\bf FinSet}
`$

これらは次の図式を可換にするとします。

$`\require{AMScd}
\begin{CD}
H(\alpha) @>{f_H}>> H(\beta)\\
@V{\pi_\alpha}VV @V{\pi_\beta}VV\\
V(\alpha) @>{f_V}>> V(\beta)\\
\end{CD}\\
\text{commutative in }{\bf FinSet}\\
\begin{CD}
H(\alpha) @>{f_H}>> H(\beta)\\
@V{\sigma_\alpha}VV @V{\sigma_\beta}VV\\
H(\alpha) @>{f_V}>> H(\beta)\\
\end{CD}\\
\text{commutative in }{\bf FinSet}
`$

半グラフ達と準同型写像達は圏を形成しますが、ここでは、可逆な準同型写像だけを考えます。半グラフを対象として可逆な準同型写像を射とする亜群（すべての射が可逆である圏）を $`{\bf SemiGraphG}`$ とします。最後の $`{\bf G}`$ は groupoid の 'g' です。次の関係があることに注意してください。

$`\quad \mrm{Mor}({\bf CSemiGraph}) = \mrm{Obj}({\bf SemiGraphG})\\
\quad \mrm{Obj}({\bf CSemiGraph}) \subseteq \mrm{Obj}({\bf SemiGraphG})
`$

亜群 $`{\bf SemiGraphG}`$ の射を、半グラフのアルファ変換〈alpha conversion〉と呼ぶことにします。「アルファ変換」はラムダ計算で使う言葉ですが借用します。どことなく雰囲気が似てる気がするからです。半グラフ圏 $`{\bf CSemiGraph}`$ の射と区別するために、半グラフのアルファ変換は次のように書くことにします。

$`\quad f = (f_V, f_H) \;: \alpha \overset{\to}{\sim} \beta \In {\bf SemiGraphG}`$

2つの半グラフのあいだにアルファ変換があれば、それらの半グラフは同一視可能だと言えます。

亜群 $`{\bf SemiGraphG}`$ にも、半グラフの直和により対称モノイド構造を与えることができます。対称モノイド亜群であることを強調したいときは $`({\bf SemiGraphG}, + , {\bf 0})`$ と書きます。たいていは、暗黙に対称モノイド構造も仮定します。

植物の林

ファミリーについては（必要があれば）以下の記事を参照してください。

• 射ファミリーと圏論的コンビネータ // ファミリーの圏
• 一般化されたファミリーの圏

$`\cat{S}`$ は集合圏の部分圏として、$`\cat{C}`$ を任意の圏とします。$`\cat{S}`$ の対象をインデキシング集合として、$`\cat{C}`$ に値を持つファミリーの圏を、

$`\quad \mrm{Fam}^{\cat{S}}(\cat{C})`$

と書くことにします。ファミリーのターゲットとなる圏 $`\cat{C}`$ として、ここでは次の圏（亜群）を考えます。

• $`{\bf PlantG}`$ ： 植物（連結な半グラフ）を対象としてアルファ変換を射とする亜群

インデキシング集合と射を、有限集合と同型写像に限定すると、次のようなファミリーの圏ができます。$`{\bf FinSetG}`$ は有限集合と同型写像の亜群です。

$`\quad \mrm{Fam}^{\bf FinSetG}({\bf PlantG}) \;\in |{\bf CAT}|`$

このファミリーの圏は亜群となり、“半グラフを対象としてアルファ変換を射とする亜群”と圏同値となります。圏同値を与える2つの関手は $`\sum`$ と $`\mrm{CP}`$ （すぐ後で説明）です。

$`\quad\xymatrix@C+2pc {
\mrm{Fam}^{\bf FinSetG}({\bf PlantG})
\ar@/^2pc/[r]^-{\sum}
& {\bf SemiGraphG}
\ar@/^2pc/[l]^-{\mrm{CP}}
}`$

$`\mrm{Fam}^{\bf FinSetG}({\bf PlantG})`$ の対象であるファミリーは次のように書きます。

$`\quad F = (I, F) = (F(i))_{i\in I}`$

ここで、

• $`I`$ は有限集合、
• $`F(i)`$ は $`{\bf PlantG}`$ の対象なので植物（連結な半グラフ）。

$`\sum(F)`$ は次のように定義します。

$`\quad \sum(F) = \sum( (I, F) ) := \sum_{i\in I}F(i)`$

定義の右辺は、対称モノイド圏としての $`{\bf SemiGraphG}`$ における有限直和です。この有限直和は、有限余極限なので一意には決まりません。今は、インデキシング有限集合 $`I`$ ごとに、ひとつの有限直和が選択特定されると考えてください。そう考えると、$`\sum( F )`$ は特定の半グラフとして一意に確定します。

$`\mrm{Fam}^{\bf FinSetG}({\bf PlantG})`$ の対象に対して定義された $`\sum`$ を射（可逆射）にも拡張するのは容易です。対象と射に対して定義された $`\sum`$ が関手となることも分かります。

次に、任意の半グラフから植物のファミリーを作ります。半グラフ $`\alpha`$ に対して、ファミリー $`\mrm{CP}(\alpha)`$ を次のように定義します。

$`\quad \mrm{CP}(\alpha) := (C(\alpha), P_\alpha)`$

ここで、

• $`C(\alpha)`$ は、半グラフ $`\alpha`$ の連結成分の集合、
• $`P_\alpha : C(\alpha) \to |{\bf PlantG}|`$ は、連結成分である部分半グラフを対応させる写像。

連結成分である部分半グラフは、定義より植物です。対応 $`\mrm{PC}`$ を関手に仕立てることができます。

2つの関手 $`\sum`$ と $`\mrm{CP}`$ により、2つの亜群 $`\mrm{Fam}^{\bf FinSetG}({\bf PlantG})`$ と $`{\bf SemiGraphG}`$ は圏同値になります（詳細は割愛）。

$`\mrm{Fam}^{\bf FinSetG}({\bf PlantG})`$ の対象、つまり植物の有限ファミリー〈finitely indexed family of plants〉を植物林〈plant forest〉とも呼びます。次のように命名します。$`{\bf GRPD}`$ は大きい〈小さいとは限らない〉亜群達の2-圏です。

$`\quad {\bf PlantForestG} := \mrm{Fam}^{\bf FinSetG}({\bf PlantG}) \;\in |{\bf GRPD}|`$

名前の末尾の'G'は亜群であることの目印です。先に述べた圏同値から、植物林の亜群は半グラフの亜群と圏同値です。

$`\quad {\bf PlantForestG} \simeq {\bf SemiGraphG} \In {\bf GRPD}`$

$`{\bf PlantForestG}`$ に、ファミリーの直和による対称モノイド構造を入れると、対称モノイド亜群としての同値に精密化できます。

$`\quad ({\bf PlantForestG}, +, {\bf 0} ) \simeq ({\bf SemiGraphG}, +, {\bf 0}) \In {\bf SymMonGRPD}`$

圏同値である2つの圏は、圏論的には区別する必要がないので、植物林の扱いと半グラフの扱いは同じです。

様々な林亜群

植物（連結な半グラフ）を対象として、アルファ変換を射とする亜群（すべての射が可逆である圏）が $`{\bf PlantG}`$ でした。この植物亜群の部分亜群を考えます。そして、部分亜群に対する林も考えます。

植物のなかで可縮〈contractible〉なものをツリー〈木 | tree〉と呼びます。可縮とは、サイクル（無向サイクル）を持たないことです。例えば、次の植物のなかで、左端は可縮な植物（つまりツリー）、残りの2つはサイクルを持つので可縮ではありません。

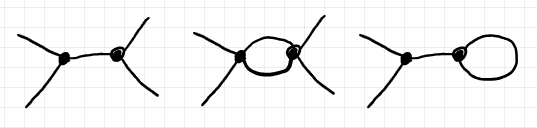
すべてのツリーとのそのあいだのすべてのアルファ変換を考えると、植物亜群 $`{\bf PlantG}`$ の部分亜群となります。これを、$`{\bf TreeG}`$ とします。

$`\quad {\bf TreeG} \subseteq {\bf PlantG} \In {\bf GRPD}`$

亜群 $`{\bf TreeG}`$ をターゲットとして有限インデキシング集合のファミリーを作れます。それらのファミリー達とファミリーのあいだの同型射〈可逆射〉は亜群を形成します。この亜群をツリー林〈tree forest | forest of trees〉の亜群と呼びます。

$`\quad {\bf TreeForestG} := \mrm{Fam}^{\bf FinSetG}({\bf TreeG}) \;\in |{\bf GRPD}|`$

この定義から、ツリー林亜群は植物林亜群の部分亜群となります。

$`\quad {\bf TreeForestG} \subseteq {\bf PlantForestG} \;\In {\bf GRPD}`$

前節で定義した関手 $`\sum`$ を、$`{\bf TreeForestG}`$ に制限した関手を $`\sum'`$ とします。

$`\xymatrix@C+2pc@R+1pc {
{\bf PlantForestG} \ar[r]^-{\sum}
& {\bf SemiGraphG}
\\
{\bf TreeForestG} \ar@{^{(}->}[u] \ar[ur]_{\sum'}
}\\
\text{commutative in }{\bf GRPD}
`$

関手 $`\sum'`$ の本質像〈essential image〉を $`{\bf TreeForestG'}`$ とします。すると、次のような圏同値と包含の関係ができます。

$`\quad {\bf PlantForestG} \supseteq{\bf TreeForestG} \In {\bf GRPD}\\
\quad {\bf TreeForestG}\simeq {\bf TreeForestG'} \In {\bf GRPD}\\
\quad {\bf TreeForestG'} \subseteq {\bf SemiGraphG} \In {\bf GRPD}
`$

対称モノイド構造まで含めた同値は次のようになります。

$`\quad ({\bf TreeForestG}, +, {\bf 0}) \simeq ({\bf TreeForestG'}, +, {\bf 0}) \In {\bf SymMonGRPD}`$

$`{\bf TreeForestG}`$ と $`{\bf TreeForestG'}`$ は区別するのがむしろ困難なので同一視します。

以上の手順は、$`{\bf TreeG}`$ 以外の $`{\bf PlantG}`$ の部分亜群に対しても適用できます。$`{\bf CorollaG}`$ を、カローラ（頂点がひとつだけで自己ループ辺を持たない半グラフ）達を対象とする部分亜群（充満部分圏）だとします。同じ手順で次の亜群を構成できます。

• $`{\bf CorollaForestG}`$ ： ファミリーとしてのカローラ林とアルファ変換の亜群
• $`{\bf CorollaForestG'}`$ ： 半グラフ亜群の部分亜群とみなしたカローラ林とアルファ変換の亜群

これら2つのの亜群は同一視できるし、直和による対称モノイド構造も入ります。

さて、植物 $`\alpha`$ があるとき、$`\alpha`$ のテール（外部辺と一対一対応）のひとつ $`r\in T(\alpha)`$ を指定した構造 $`(\alpha, r)`$ を根付き植物〈rooted plant〉と呼びます。指定したテール $`r`$ をルート〈根 | root〉と呼びます。ルート以外のテール（外部辺と考えてもよい）はリーフ〈葉 | leaf〉です。ルートもリーフもテール（あるいは外部辺）であることに注意してください。

すべての根付き植物達を対象として、ルートを保存する（ルートをルートに移す）アルファ変換達を射とする亜群ができます。これを $`{\bf RPlantG}`$ とします。'R' は rooted の意味です。$`{\bf RPlantG}`$ は、$`{\bf PlantG}`$ の部分亜群にはなりませんが、ルートを忘れる忘却関手を持ちます。

$`\quad U: {\bf RPlantG} \to {\bf PlantG} \In {\bf GRPD}`$

根付き植物の林は、有限ファミリーとして定義できます。根付き植物林の亜群〈rooted plant groupoid | groupoid of rooted plants〉は次です。

$`\quad {\bf RPlantForestG} := \mrm{Fam}^{\bf FinSetG}({\bf RPlantG})\;\in |{\bf GRPD}|`$

$`{\bf RPlangG}`$ の部分亜群として、次が考えられます。

• $`{\bf RTreeG}`$ ： 根付き木とルートを保存するアルファ変換の亜群
• $`{\bf RCorollaG}`$ ： 根付きカローラとルートを保存するアルファ変換の亜群（根付きカローラ（頂点がひとつだけの根付きツリー）は低木〈shrub〉とも呼びます。）

これらの亜群からも、林〈有限ファミリー〉の亜群を構成できます。

• $`{\bf RTreeForestG}`$ ： 根付き木林と（林の）アルファ変換の亜群
• $`{\bf RCorollaForestG}`$ ： 根付きカローラと（林の）アルファ変換の亜群

林の亜群には、林の直和により対称モノイド構造が入ります。

植物亜群や根付き植物亜群の部分亜群や、その変種は色々と考えることができます。それらの亜群に林〈有限ファミリー〉を作る構成をすることにより、対応する対称モノイド亜群を得ることができます。

コステロの半グラフ圏はいったい何なのか？

「亜群をベースとする圏類似構造： コステロの事例」で述べたように、コステロの半グラフ圏 $`{\bf CSemiGraph}`$ は、定義を見る限り圏にはなっていません。では、$`{\bf CSemiGraph}`$ はいったい何なんでしょう？

ひとつの案として、ちゃんとした圏になるように定義を修正することが考えられます。対象の集合／射の集合に同値関係を入れて商集合を作り、商集合のレベルでは圏になるようにする、とか。あるいは、対象の亜群／射の亜群の骨格を見つけて、骨格上で議論をするとか、です。なんらかの細工をしてちゃんとした圏（普通の圏）にしよう、というアプローチですね。

僕は、「ちゃんとした圏にしよう」アプローチを採用する気はありません。ちゃんとしてない、ゆるゆるな部分がコステロ半グラフ圏の面白いところだと思うからです。ゆるゆるの部分を捨てないで、そのまま定式化したいのです。この方向での別な案は、コステロ半グラフ圏を、対称モノイド二重圏〈symmetric monoidal double category〉とみなす方法です。

ここで使う二重圏は、縦射〈vertical morphism〉と2-射〈2-morphism | double morphism〉が（縦方向に）可逆なものです。横射〈horizontal morphism〉と横方向に見た2-射は可逆とは限りません。このタイプの二重圏は、亜群の圏のなかの内部圏〈internal category〉ですが、内部圏の概念を使わずに具体的に定義します。

二重圏は2つの圏から構成されます。$`\cat{G}, \cat{D}`$ を2つの圏とします。次のように、書き方の約束をします。

• $`\cat{G}_0 := \mrm{Obj}(\cat{G})`$
• $`\cat{G}_{1v} := \mrm{Mor}(\cat{G})`$
• $`\cat{D}_{1h} := \mrm{Obj}(\cat{D})`$
• $`\cat{D}_{2} := \mrm{Mor}(\cat{D})`$

これらの集合の要素を次のように呼びます。

• $`\cat{G}_0 := \mrm{Obj}(\cat{G})`$ の要素を（二重圏）の対象〈object〉と呼ぶ。
• $`\cat{G}_{1v} := \mrm{Mor}(\cat{G})`$ の要素を（二重圏）の縦射〈vertical morphism〉、または単に射〈morphism〉と呼ぶ。
• $`\cat{D}_{1h} := \mrm{Obj}(\cat{D})`$ の要素を（二重圏）の横射〈horizontal morphism〉、またはプロ射〈proarrow〉と呼ぶ。
• $`\cat{D}_{2} := \mrm{Mor}(\cat{D})`$ の要素を（二重圏）の2-射〈2-morphism〉または二重射〈double morphism〉と呼ぶ。

$`\cat{G}, \cat{D}`$ は圏なので、圏としての構造は次のように与えられます。以下で、$`X\FProd{f}{A}{g} Y`$ はファイバー積です。$`{\bf SET}`$ は大きい〈小さくないかも知れない〉集合の圏です。

$`\xymatrix@C+1pc {
\cat{G}_{1v} \ar@/^1.5pc/[r]^{\mrm{dom} } \ar@/_1.5pc/[r]_{\mrm{cod}}
& \cat{G}_0 \ar[l]_{\mrm{id} }
\\
\cat{G}_{1v} \FProd{\mrm{cod}} {\cat{G}_0 } {\mrm{dom}} \cat{G}_{1v}
\ar[r]^-{(;)}
& \cat{G}_{1v}
}\\
\text{ in }{\bf SET}
`$

$`\xymatrix@C+1pc {
\cat{D}_{2} \ar@/^1.5pc/[r]^{\mrm{src} } \ar@/_1.5pc/[r]_{\mrm{trg}}
& \cat{D}_{1h} \ar[l]_{\mrm{vid} }
\\
\cat{D}_{2} \FProd{\mrm{trg}} {\cat{D}_{1h} } {\mrm{src}} \cat{D}_{2}
\ar[r]^-{(;)}
& \cat{D}_{2}\\
}\\
\text{ in }{\bf SET}
`$

$`\cat{D}`$ のほうは、$`\mrm{dom}, \mrm{cod}, \mrm{id}`$ の代わりに $`\mrm{src}, \mrm{trg}, \mrm{vid}`$ を使ってますが、名前を変えているだけで、通常の圏の構造を持ちます。$`\mrm{vid}`$ の 'v' は vertical のつもりです。

これだけだと、単に2つの圏が独立してあるだけです。さらに、2つの圏を結びつける関手があります。$`{\bf CAT}`$ は大きい〈小さくないかも知れない〉圏の2-圏です。以下で、$`\dimU{\bf CAT}{1}`$ は、2-圏の2-射を捨てた1-圏です。$`\dimU{\text{－}}{1}`$ については「圏の次元調整」を参照してください。

$`\xymatrix@C+1pc {
\cat{D} \ar@/^1.5pc/[r]^{\mrm{left} } \ar@/_1.5pc/[r]_{\mrm{right}}
& \cat{G} \ar[l]_{\mrm{hid} }
\\
\cat{D} \FProd{\mrm{right}} {\cat{G} } {\mrm{left}} \cat{D}
\ar[r]^-{(*)}
& \cat{D}\\
}\\
\text{ in }\dimU{\bf CAT}{1}
`$

$`\mrm{left}, \mrm{right}, \mrm{hid}`$ は関手です。通常の大きい圏は、ファイバー積を持つ圏 $`{\bf SET}`$ 内の圏対象ですが、$`(\cat{G}, \cat{D}, \mrm{left}, \mrm{right}, \mrm{hid}, (*))`$ は、ファイバー積を持つ圏 $`\dimU{\bf CAT}{1}`$ 内の圏対象です。つまり、可換図式で書かれた圏の公理を満たします。このとき、$`(\cat{G}, \cat{D}, \mrm{left}, \mrm{right}, \mrm{hid}, (*))`$ を二重圏〈double category〉といいます。

二重圏はなかなかにややこしい構造です。以下の過去記事で二重圏を扱っています。

• グリッド計算とコーナリング、そして二重圏
• 二重圏のストリング図の描画方向
• 二重圏を語るために
• 二重圏の語法・記法、ローカルルール事例

コステロの半グラフ圏においては：

• $`\cat{G}`$ に相当する圏は、カローラ林を対象として、カローラ林のあいだのアルファ変換を射とする亜群 $`{\bf CorollaForestG}`$
• $`\cat{D}`$ に相当する圏は、半グラフを対象として、半グラフのあいだのアルファ変換を射とする亜群 $`{\bf SemiGraphG}`$
• 横結合 $`(*)`$ は、射とみなした半グラフ〈横射〉の結合〈グラフ置換〉、2-射〈アルファ変換〉に対する同様な操作。

さらに、対象、縦射、横射、2-射に対して対称モノイド積が定義できて、全体として対称モノイド二重圏となります。縦射と縦方向の2-射は可逆なので、対称モノイド縦可逆二重圏〈symmetric monoidal vertically-invertible double category〉と言えば正確です。

結局、コステロ〈Kevin Costello〉が定義した“半グラフの圏”は、実際には“半グラフの対称モノイド縦可逆二重圏”だったと言えそうです。

二重関手意味論

ローヴェア〈William Lawvere〉によれば、代数系の概念は、“セオリー”と呼ばれる圏により記述されます。セオリーが代数系の種類〈クラス〉を定義して、セオリーからの関手が代数系のインスタンスになります（「ローヴェア・セオリーとその周辺」参照）。これが関手意味論〈functorial semantics〉の発想です。

もともとコステロは、半グラフの対称モノイド縦可逆二重圏を、圏類似代数系〈category-like algebraic system | CLAS〉を定義するために導入しました。この特殊な二重圏がセオリーに相当します。セオリー二重圏〈theory double category〉と呼んでいいでしょう。セオリー二重圏が圏類似代数系の種類〈クラス〉を定義して、セオリー二重圏からの二重関手〈double functor〉が圏類似代数系のインスタンスになります。二重関手意味論〈double functorial semantics〉というわけです。

コステロの定義（その他多くの場合）では、圏類似代数系のインスタンスは対称モノイド圏への関手で与えられます。単なる対称モノイド圏と関手では、二重関手意味論になりません。しかし、対称モノイド圏 $`\cat{V} = (\cat{V}, \otimes, I)`$ があれば、簡単に対称モノイド二重圏を構成できます。可換な四角形を2-射にすればいいのです。特に、縦方向の射を可逆射に限定すれば、対称モノイド縦可逆二重圏を作れます。

半グラフの二重圏（正確には対称モノイド縦可逆二重圏）を $`{\bf SemiGraphDC}`$ とします。対称モノイド圏 $`\cat{V}`$ から作られた対称モノイド縦可逆二重圏を $`\mrm{VInvDouble}(\cat{V})`$ とすると、圏類似代数系のインスタンス〈モデル | 表現〉は次の形になります。

$`\quad A: {\bf SemiGraphDC} \to \mrm{VInvDouble}(\cat{V}) \In {\bf SymMonDoubleCAT}`$

$`{\bf SymMonDoubleCAT}`$ が2-圏となるので、インスタンス〈モデル | 表現〉の全体は圏になります。

関手意味論では、セオリーとターゲット圏からモナドを構成できて、セオリーのインスタンス〈モデル | 表現〉達の圏は、モナドのアイレンベルク／ムーア圏と圏同値になります（リントンの定理〈Linton theorem〉）。二重関手意味論でも同様な結果が欲しいなら、まずはモナド（あるいは2-モナド）を構成する必要があります。そのためには、対称モノイド縦可逆二重圏と対称モノイド二重関手の構造をもっと詳しく調べることが課題です。（有向コンテナ（「有向コンテナと多項式コモナド」参照）を双対にした余有向コンテナが役立ちそうな気がしています。）