「オペラッド〈operad〉」という言葉は非常によく使われるのですが、僕は「オペラッド」の同義語として「複圏〈multicategory〉」を好んで使っていました。その理由は、「圏〈category〉 → 複圏〈multicategory〉 → 多圏〈polycategory〉」というきれいな拡張の系列があるからです。
しかし最近は、圏に似てるけど圏ではないものは何でもオペラッドでいいかな、と思うようになりました。つまり、「オペラッド=圏もどき」です。この用法だと、オペラッドの意味はあやふやで曖昧なものになります。が、むしろ定義を曖昧にしたいときに「オペラッド」を使う、という方針です。僕だけでなく、「オペラッド」をそんなふうに使う人が増えていそうです。一方、「複圏」は、オペラッドのなかでも定義がハッキリしたものを指すことにします。
というわけで、「オペラッドの話」とは、圏に似たなんか曖昧なものについて話す、ということです。曖昧なものをハッキリさせるにはどうしたらいいか? という問題意識もあります。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\u}[1]{\underline{#1}}
%\newcommand{\o}[1]{\overline{#1}}
\newcommand{\hyp}{\text{-} }
\newcommand{\id}{\mathrm{id}}
\newcommand{\In}{\text{ in } }
\newcommand{\act}[2]{ \mathop{_{#1} \cdot_{#2}} }
\newcommand{\twoto}{\Rightarrow }
`$
内容:
オペラッドの事例
オペラッドとは「なんか曖昧なもの」だけでは、さすがにひど過ぎるので、オペラッドと呼べるモノのなかで一番簡単だと思われる事例を紹介します。
$`\cat{O}`$ は、自然数に集合を対応付ける写像とします。
$`\quad \cat{O} : {\bf N} \to |{\bf Set}| \In {\bf SET}\\
\text{i.e.}\\
\quad \text{For }n \in {\bf N},\; \cat{O}(n) \in |{\bf Set}|
`$
3つの自然数、$`n, m, k`$ で $`1 \le k \le n`$ であるものに対して、写像 $`\gamma_{n, m, k}`$ が対応しています。
$`\quad \gamma_{n, m, k}: \cat{O}(m)\times \cat{O}(n) \to \cat{O}(n - 1 + m) \In {\bf Set}`$
下付きの $`n, m`$ はしばしば省略されます。また、$`\gamma_k`$ を中置演算子記号 $`(\hyp \,;k \hyp)`$ で書きます。
$`\quad (\hyp \,;_k \hyp) : \cat{O}(m)\times \cat{O}(n) \to \cat{O}(n - 1 + m) \In {\bf Set}`$
$`(\hyp \,;k \hyp)`$ は図式順記法だったので、反図式順なら $`(\hyp \circ_k \hyp)`$ を使います。
$`\quad (\hyp_\mrm{second} \circ_k \hyp_\mrm{first}) : \cat{O}(m)\times \cat{O}(n) \to \cat{O}(n - 1 + m) \In {\bf Set}`$
反図式順を、記法が逆転してるのではなくて実際にそうなのだ、と考える人もいます。そのときは:
$`\quad (\hyp_\mrm{first} \circ_k \hyp_\mrm{second}) : \cat{O}(n)\times \cat{O}(m) \to \cat{O}(n - 1 + m) \In {\bf Set}`$
どうでもいいことだけど、ややこしい。僕は図式順の信奉者です。
$`\cat{O}, \gamma`$ の解釈(事例)のひとつとして、基本演算子記号から組み立てられた“$`n`$項の式”の集合を $`\cat{O}(n)`$ だとします。例えば、基本演算子記号として、
- 足し算 $`+`$ : 2項演算子記号
- 符号の反転 $`-`$ : 1項演算子記号、引き算ではない
- 定数 $`0, 1`$ : 0項演算子記号
これらから組み立てられた$`n`$項の算術式の集合を $`\cat{O}(n)`$ とします。プレースホルダーに(ハイフンでは混乱するので)'$`\bullet`$' を使うことにして、$`\cat{O}(n)`$ の要素を幾つか挙げてみます。
- $`1 \in \cat{O}(0)`$
- $`(+) = (\bullet + \bullet) \in \cat{O}(2)`$
- $`a := (\bullet + 1) \in \cat{O}(1)`$
- $`b := (1 + 1) \in \cat{O}(0)`$
- $`c := ( ( (\bullet + (- \bullet)) + \bullet) + 1) \in \cat{O}(3)`$
オペラッドに備わった $`;k`$(または $`\circ_k`$)は、$`k`$番目のプレースホルダーに代入をして新しい式を作る操作です。
- $`1 \,;_2 (+) = (+) \circ_2 1 = a`$
- $`1 \,;_1 a = a \circ_1 1 = b`$
- $`a \,;_3 c = c \circ_3 a = ( ( (\bullet + (- \bullet)) + (\bullet + 1) ) + 1)`$
算術式を構文解析するとツリーになります(「構文的モナド」参照)。このオペラッドは、ツリーと接ぎ木〈grafting〉の計算体系になっています。
写像の族 $`\circ_{\hyp} = \gamma_{\hyp, \hyp, \hyp}`$ に関して、次の法則を要求します。
$`\text{For } h \in \cat{O}(n), f \in \cat{O}(l), g\in \cat{O}(m)\\
\text{For } 1\le i \lt j \le n\\
\quad (h \circ_i f) \circ_{l - 1 + j} g = (h \circ_j g) \circ_i f
`$
この法則が言ってることは; まず、次のような素材があったとします。
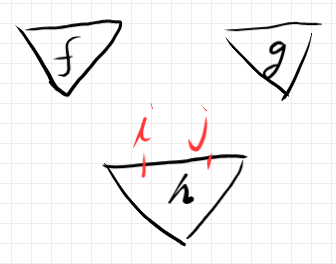
次のように二種類のやり方で組み合わせます。法則は、上段の結果と下段の結果は等しいと主張しています。これは、並列同時結合がうまく定義できることを保証します。
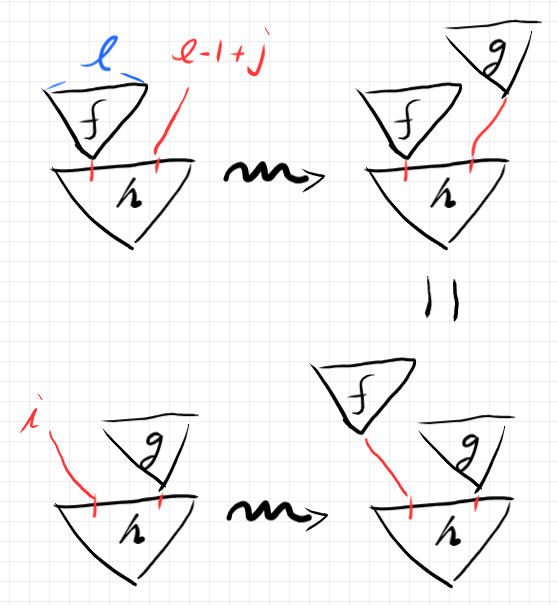
もうひとつ、次の法則も要求します。
$`\text{For } h \in \cat{O}(n), g\in \cat{O}(m), f \in \cat{O}(l) \\
\text{For } 1\le i \lt m, 1 \lt j \lt n\\
\quad h \circ_j (g \circ_{i} f) = (h \circ_j g)\, \circ_{j - 1 + i} f
`$
先の法則と同様に、まず、次のような素材があったとします。
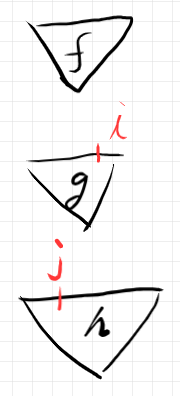
次のように二種類のやり方で組み合わせます。法則は、上段の結果と下段の結果は等しいと主張しています。これは、直列順次結合がうまく定義できることを保証します。
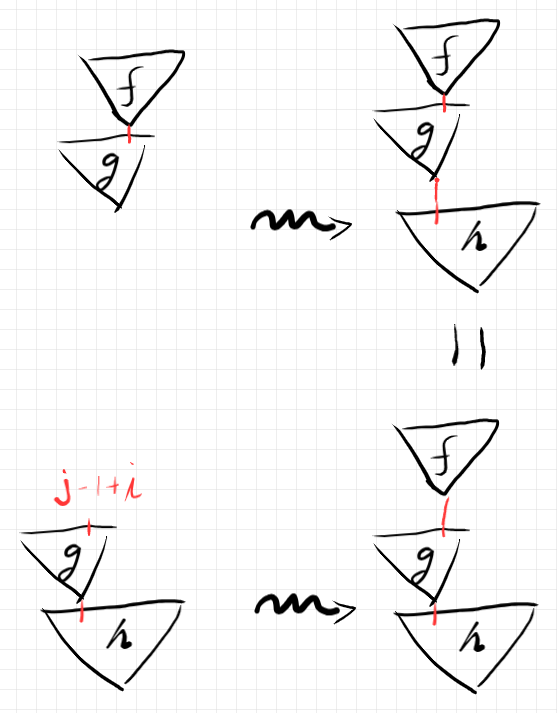
恒等に関する法則もありますが、それは次節で述べます。
オペセットと算子
前節の例では、集合 $`\cat{O}(n)`$ の要素は、基本演算子記号を組み合わせた“広義の演算子”と言えます。つまり、集合 $`\cat{O}(n)`$ は(広義の)$`n`$項演算子の集合となります。演算子〈operation | operator〉の集合なので、operation set(または operator set)ですが、短くオペセット〈opeset〉と呼びます。オペセットの要素は演算子ですが、先頭の「演」を削って算子〈ration | rator〉と呼ぶことにします。この呼称を選んだ事情は以下の補足に書いておきます。
「ホムセット」「射」という言葉は非常に使い勝手がいいです。国語辞書に載ってないし、他の分野で使われることもないので、何も連想できないことが使い勝手がいい理由です。
準同型射〈homomorphism〉は、若干特定の意味が付着してます。これを、'hom'(なぜか 'o' は落ちた)と 'morphism' に分割して、homset, morphism とするといい具合に意味不明となり、余計な連想を誘発しない用語になります。
同様に、演算子〈operation | operator〉を、'ope' と 'ration'(または 'rator')に分割して、opeset, ration(または rator)とするといい具合に意味不明でしょう。オペセットの要素は "operation" の先頭部分を削っているので、日本語でも「演算子」の先頭部分を削って「算子」です。
opeset はともかく、ration, rator は奇妙かも知れません。しかし、適用構造〈application structure〉で、rator〈演算子〉と rand〈被演算子〉という言葉を使うことがあるので、新規の造語というわけでもありません。
[/補足]
前節に登場した $`;k`$(または $`\circ_k`$)はオペラッド結合〈operadic composition〉または単に結合〈composition〉と呼びます。前節で述べた法則が、結合に関する法則〈公理〉です。前節の法則はまとめて結合法則〈associative laws〉と呼ぶこともありますが、モノイド圏との類似でいえば、一番目が交替法則〈interchange law〉で、二番目が結合法則〈associative law〉に近いでしょう。
さて、オペラッドでも単位元と単位法則がありそうです。実際あります。オペラッドのオペセット $`\cat{O}(1)`$ に特別な算子(要素) $`\mrm{i}\in \cat{O}(1)`$ があるとします。この特別な算子は次の法則を満たします。
$`\text{For } f\in \cat{O}(n),\, 1\le k \le n\\
\quad f \circ_k \mrm{i} = f\\
\quad \mrm{i} \circ_1 f = f
`$
特別な $`\mrm{i} \in \cat{O}(1)`$ を恒等算子〈identity {ration | rator}〉または単に恒等〈identity〉と呼びます。
恒等を単位と呼ぶと混乱するかも知れません。恒等とは別に、“横方向”の単位〈horizontal unit〉が存在することもあるからです。もし単位と呼びたいなら垂直単位〈vertical unit〉というのが無難です。
オペラッドには恒等を要求しますが、恒等を持たないオペラッドを考えることもあります。恒等を持たない〈要求しない〉の意味で非単位的〈non-unital〉を使います。垂直単位を持たないことであり、水平単位ではありません(水平単位はそもそも要求してないし)。
オペラッドとは
前の2節で述べたことは、特定の簡単なオペラッドの紹介と、一般的な用語の導入です。「オペラッドとは何であるか?」には答えていません。オペラッドの意味が拡散しすぎて、もはや「ここまでがオペラッド」という境界線を引くのは困難なので、冒頭で言ったように「オペラッド」は曖昧なままでいとします。しかし、オペラッドの分類はしましょう。
オペラッドの分類を考える際にオパトビッチの次の論文は参考になります。
- [Obr18-]
- Title: Cyclic operads: syntactic, algebraic and categorified aspects
- Author: Jovana Obradovic
- Submitted: 7 Jan 2018
- Pages: 146p
- URL: https://hal.science/tel-01676983/document
例えば、biased vs. unbiased のような二分類法〈dichotomy〉が提案されています。二分類のどちらかである「◯◯◯」に対して、「◯◯◯な☓☓☓」という語句が色々使われていました。「unbiasedな☓☓☓」として、次のような言い回しがありました。
- the unbiased definition
- the unbiased approach
- the unbiased framework
- the unbiased manner
- the unbiased way
- the unbiased version
- the unbiased variant
- the unbiased characterisation
- the unbiased presentation
- the unbiased setting
- the unbiased notion of ...
オパトビッチの観点を参考にすると、次のようなニ分類の軸があります(オパトビッチがほとんど言及してない項目もありますが)。
- メタレベル vs. オブジェクトレベル
- 単色 vs. 多色
- 骨格的 vs. 非骨格的
- 対称 vs. 非対称
- 単純結合 vs. フル結合
- 公平 vs. 偏向
- 豊穣 vs. 無豊穣
- 厳密法則 vs. 弱法則
色々なオペラッド
前節で出したニ分類の軸(分類基準)についてザッと説明します。
メタレベル vs. オブジェクトレベル
マイクロコスモ原理〈microcosm principle〉と呼ばれる原理(おそらく経験則)があります(例えば、「マイクロコスモ原理と構造の無限タワー」参照)。おおよそ次のようなことです。
- ある代数的構造(例:モノイド)を定義するとき、その前に、環境となる圏(例:モノイド圏)が必要となる。
真面目に考えると夜も眠れなくなる話なのですが、現象・事実としてのマイクロコスモ原理には頻繁に遭遇します。
オペラッド概念に対してもマイクロコスモ原理は適用できて、「オペラッドを定義するにはメタレベルのオペラッドが必要になる」のです。マイクロコスモ原理の縁起や解釈に悩まないとしても、テクニカルに厄介な話です。オブジェクトレベルのオペラッドを定義するためにメタレベルのオペラッドを使うのですが、しばしば混乱します。
運用のtipsとしては、オブジェクトレベルのオペラッド(圏類似構造)を定義する環境/定義デバイス〈defining device / machinery〉としてのメタレベル・オペラッドはあまり複雑にしないほうがいいようです。比較的に単純なメタレベル・オペラッドを使っても、複雑で多様なオブジェクトレベル・オペラッドを定義できます。
最近考えているスケマティック系(「スケマティック系のために: 雑多な予備知識 // 絵図的手法とスケマティック系」参照)は、メタレベル・オペラッドを含むのですが、単純さと表現力〈expressive power〉のトレードオフが要〈かなめ〉だと思っています。
単色 vs. 多色
先に挙げた簡単なオペラッドでは、広義の演算子の引数の個数〈項数 | arity〉はありましたが、引数の型は考えてません。オペラッドにおける色〈color〉とは、引数や戻り値の型(に相当する概念)のことです。
型付き〈typed〉と同じ意味で色付き〈colored〉が使われます。色を考えないときは色無し〈uncolored〉ですが、実際は色がひとつしかないことです。なので、uncolored ではなくて unicolored あるいは single-colored とも言われます。single -colored〈単色〉との対比からは many-colored〈多色 | multi-colored〉がいいでしょう。
「色彩的抽象テンソルシステムと圏類似代数系」の注釈に書いたように、スピシーズ(テクニカルターム)と組み合わせた colored species なんかは、センシティブな解釈もあり得るので、colorful〈色彩的〉 がいいような気がします。色がひとつしかないほうは monochrome〈単彩的〉です。
言葉の問題はさておいて、色の扱いは難しいです。色を、どのタイミングでどんな方法で導入するかの判断が難しい。色に、符号〈極性〉と対合〈否定〉を組み込んだ色パレット〈color palette〉を使う方法もあります(「コレクション、対称性、シーケンス、色付け // 色パレット」参照)。しかし、色パレットがいつも最適とも限らないようです。
具体的な状況で出てくる集合の要素が、(引数の)位置やラベルなのか、それとも色〈型〉なのか判断に苦しんだり、混乱することもあります。
骨格的 vs. 非骨格的
色を考えない場合(正確には唯一つの色しかない場合)、算子(オペセットの要素)を特徴付けるプロファイルは引数の個数〈項数 | arity〉だけです。個数は自然数で表せるので、オペセットは $`\cat{O}(n)`$ のように書けたわけです。
引数〈仮引数 | プレースホルダー〉にラベル〈名前〉を付けるとすると、単なる自然数ではなくてラベルのリストが算子のプロファイルになります。ラベルのリストとは、有限全順序集合と考えられるので、ありとあらゆる有限全順序集合をプロファイルとして考える必要があります。
算子の項数/プロファイルを自然数で済ませる方式が骨格的〈skeletal〉です。すべての有限全順序集合やすべての有限集合を考える方式は非骨格的〈non-skeletal〉です。骨格的とは、圏全体ではなくて圏の骨格を使っているからです(「圏の骨格の扱い方: 線形代数を例として」参照)。
骨格的方法と非骨格的方法は、(知られている状況では)同値になりますが、それぞれのメリット・デメリットがあります。
対称 vs. 非対称
オペラッドが対称〈symmetric〉だとは、オペセットに対称群〈symmetric group〉の作用があることです。この作用は、引数の順番を変える操作と連動しています。非対称〈non-symmetric〉の場合は、群作用は考えません。
オペラッドの定義に対称シーケンス〈symmetric sequence〉を使うことを考えると、対称群以外が出てきてもいいような気がしますが、対称群(と自明な群)以外は出てこないようです。これは何故なんでしょう? 非骨格的定式化を骨格的にすると、対称群は必然的に出現しますが、それと関係あるのでしょうか? よく分かりません。
オペラッドにおける対称性(群作用)は(少なくとも僕にとっては)、どこから来たのか不明でミステリアスです。
単純結合 vs. フル結合
オペラッド結合をワイヤーの接続と考えたとき、一本のワイヤーだけを結合することを単純結合〈simple composition〉と呼びましょう。$`n`$ 本ある入力のワイヤーに対して、$`n`$ 個の算子〈オペセットの要素〉を準備して一気に結合することを同時結合〈simultaneous composition〉、またはフル結合〈full composition〉と呼びます。過去記事「述語論理: 様々な多圏達の分類整理 // ワイヤリング規律による分類」では(少し状況が違いますが)、ナロー多結合〈narrow polycomposition〉、ワイド多結合〈wide polycomposition〉という言葉を使っていました。過去記事での「ワイド」の意味は、任意の部分結合〈partial composition〉に意味ですが。
ある条件のもとでは、単純結合によるオペラッドの定義とフル結合によるオペラッドの定義が同値になることを示せます。しかし、単純結合とフル結合による定式化はだいぶ違います。いつでも同値性が保証できるとは限らないでしょう。両方の方式を比較検討したほうがよさそうです。
公平 vs. 偏向
オペラッドにおける計算は、ツリーの接ぎ木〈grafting〉のことでした。オペラッド結合として、すべてのツリーを考えて、任意に取り出したツリー達に対して接ぎ木(オペラッド演算)を考えるのが公平な〈unbiased〉方式です。それに対して、典型的な、あるいは基本的なツリーを選び出して、それらに対する演算だけを定義するのが偏向〈biased〉方式です。
モノイドを定義する場合で言えば、0項演算(単位元)と2項演算だけを指定して定義するのが偏向方式です。すべてのn項演算(0項演算、1項演算、2項演算、3項演算、‥‥)を同時に考えて、それらのあいだの法則もすべて同時に考えるのが公平方式になります。
「単純結合 vs. フル結合」と状況は似ていて、ある条件のもとでは、公平方式でも偏向方式でも定義されるオペラッド概念は同じになります。公平方式のほうがより一般的で強力なようです。しかし一方、公平方式は、計算が面倒で取り扱いが困難になります。公平方式のための効率的な計算法が望まれます。
豊穣 vs. 無豊穣
無豊穣〈unenriched〉あるいは通常〈ordinary〉オペラッドとは、オペセットが集合であるものです。豊穣圏と同様に、オペセットに集合圏以外の対象も許すと豊穣オペラッド〈enriched operad〉になります。
頻出する豊穣オペラッドは、オペセットをベクトル空間としたものです。これは線形オペラッド〈linear operad〉とも呼ばれます。オペセットを位相空間や多様体にとることもあります。その場合、空間のホモトピー集合や高次のホモトピー構造を使うことがあります。
順序集合や距離空間は特別な豊穣圏ですが、それに倣えば、順序集合や距離空間のオペラッド・バージョンを定義できるでしょう。それがどう役に立つかはよく分かりませんが。
厳密2-圏のオペラッド・バージョンとして、小さい圏達の圏 $`{\bf Cat}`$ を対称モノイド圏とみて豊穣化した$`{\bf Cat}`$-豊穣オペラッドがあります。多項関手の計算体系として便利そうです。
厳密法則 vs. 弱法則
オペラッドの計算法則(結合法則、交替法則、単位法則)は、等式として成立すると仮定しています。つまり、法則は厳密〈strict〉です。しかし、オペセットを位相空間や圏に置き換えると、法則を等式に保つのは難しくなります。厳密とは限らない高次圏のように、オペラッドの法則を弱い〈weak〉法則にゆるめた構造が考えられます。
弱い法則を仮定すると、弱い法則を統制する高次の法則が必要になります。高次の法則は、それを見つけるのも記述するのも困難です。とたんに話が難しくなりますが、オペラッドの一般化の当然な方向ではあります。