最近の応用圏論〈ACT | Applied Category Theory〉では、モノイド圏、アクテゴリー、二重圏、三重圏などの複雑な構造を平気で使います。このような複雑な構造を扱うときは、名前に十分な注意をはらう必要があります。
複雑な構造でなくても、名前に十分な注意をはらうのは当たり前にすべきことです。しかし、「名前に注意しろ!」と百回くらい言っても、名前に無頓着なまま、なんて事も実際にあります。
そこで、この記事では、名前に色を付けたり、名前の関連性を有向グラフで図示したりして、構造が名前によってどのように記述されるかを明らかにすることにします。
今回のこの記事では、指標と名前の基本的なことを解説し、引き続く記事達では、圏、二重圏、モノイド圏、アクテゴリー、三重圏などの、より複雑な構造(の幾つか)の記述を扱う予定です。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\twoto}{ \Rightarrow }
\newcommand{\id}{ \mathrm{id} }
\newcommand{\hyp}{\text{-} }
%\newcommand{\dblcat}[1]{\mathbb{#1}}
%%
\require{color}
\newcommand{\NN}[1]{ \textcolor{orange}{\text{#1}} } % New Name
\newcommand{\NX}[1]{ \textcolor{orange}{ {#1}} } % New Name
\newcommand{\KN}[1]{ \textcolor{blue}{\text{#1}} } % Known Name
\newcommand{\KX}[1]{ \textcolor{blue}{#1} } % New EXpression
\newcommand{\VN}[1]{ \textcolor{violet}{ {#1}} } % Variable Name
\newcommand{\KO}[1]{ \mathop{\textcolor{blue}{ {#1}}} } % Known Operator
\newcommand{\T}[1]{\text{#1} }
`$
内容:
- 指標
- ターゲット: 指標を解釈する場所
- 別名と定義された名前
- 変数名
- 純指標、構成手続き
- 指標の拡大: 差分記述
- 中置演算子記号の宣言
- 名前依存性の色付き表示とグラフ表示
- 図式による法則の記述
- そしてそれから
関連記事:
指標
構成素〈constituent〉達が複合されて出来上がる構造〈structure〉を記述するための構文的対象物〈syntactic object〉は指標〈signature〉と呼びます。プログラミング言語において指標に相当する構文的対象物は、インターフェイス、型クラス、プロトコル、トレイト、コンセプト … など様々な呼び名があります。
例として、半群〈semigroup〉の指標を以下に挙げます。色についてはすぐ下で説明します。
$`\T{signature }\NN{Semigroup}\:\{\\
\quad \T{sort } \NN{U}\\
\quad \T{operation }\NN{m} : \NN{U} \KO{\times} \NN{U} \to \NN{U}\\
\quad \T{equation } \NN{assoc} ::
(\NN{m} \KO{\times} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\times} \NN{m}) \KO{;}\NN{m} \\
\}
`$
等式〈equation〉の等号が '$`=`$' でなくて '$`\twoto`$' なのが気になるかも知れませんが、等式は“圏の2-射”であることを強調して二重矢印を使っています。必要なら、以下の過去記事を参照してください。
念の為、等式 $`\T{assoc}`$ の可換図式による表現も示します(図中の名前に色は付いてません、フォントも微妙に違っています*1)。
$`\quad \xymatrix{
(U\times U)\times U \ar[r]^{\alpha_{U,U,U}} \ar[d]_{m\times \id_U}
& U\times (U \times U) \ar[d]^{\id_U \times m}
\\
U\times U \ar[d]_{m}
& U\times U \ar[d]^{m}
\\
U \ar@{=}[r]
& U
}\\
\quad \text{commutative }
`$
指標には幾つかの名前〈name | identifier〉が出現します。'$`\T{U}`$'、'$`\T{m}`$' のような一文字も名前だし、'$`\times`$'、'$`;`$' のような記号も名前だし、'$`\text{Semigroup}`$'、'$`\text{assoc}`$'、'$`\text{半群}`$' のような文字列も名前です。'$`1`$' や '$`3.14`$' のような数字〈digit〉/数表示〈numeral〉も名前とみなします。名前はラベル〈label〉とも呼ばれます。「名前」と「ラベル」は同義語です。
上の指標では、名前を色分けしています。色は次の意味です。
- オレンジ色は新規名〈new name〉: この指標で新たに導入された名前
- 青色は既知名〈known name〉: 既に知られていて、指標内で使っていい名前
色を見れば、次の名前は指標により導入された新規名だと分かります。
- $`\T{Semigroup}`$
- $`\T{U}`$
- $`\T{m}`$
- $`\T{assoc}`$
次の名前は指標内で自由に使ってもいい既知名です。
- $`\times`$ (集合の直積)
- $`\id`$ (恒等写像)
- $`\alpha`$ (集合の直積の結合律子〈associator〉)
既知名の意味と使用法は事前に約束・合意されている必要があります。そうでないと、指標を書くことが出来ないし、指標による意図・情報の伝達もうまくいかないでしょう。
上記の半群の指標の各行(3行ある)は新規名の宣言です。宣言の先頭は、何を宣言するかを明示するキーワードです。
- $`\T{sort}`$ : 宣言する名前は、型/集合を指す名前
- $`\T{operation}`$ : 宣言する名前は、関数/演算を指す名前
- $`\T{equation}`$ : 宣言する名前は、等式(として書かれた法則)を指す名前
これらのキーワードは無くても特に困らないので省略してかまいません。
$`\T{signature }\NN{Semigroup}\:\{\\
\quad \NN{U}\\
\quad \NN{m} : \NN{U} \KO{\times} \NN{U} \to \NN{U}\\
\quad \NN{assoc} ::
(\NN{m} \KO{\times} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\times} \NN{m}) \KO{;}\NN{m} \\
\}
`$
名前の細かい種別*2までは不要だが、データか法則かの区別はしたいなら、次のように書くことにします。
$`\T{signature }\NN{Semigroup}\:\{\\
\quad \T{datum } \NN{U}\\
\quad \T{datum }\NN{m} : \NN{U} \KO{\times} \NN{U} \to \NN{U}\\
\quad \T{law } \NN{assoc} ::
(\NN{m} \KO{\times} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\times} \NN{m}) \KO{;}\NN{m} \\
\}
`$
"datum" は今ではあまり意味がない "data" の単数形です。単数・複数の区別を付けるためにあえて使っています。複数形であるキーワード $`\T{data}`$ と $`\T{laws}`$ は、任意個数(2つ以上でも1つでも0個でもよい)の宣言をまとめてデータまたは法則だと指定します。
$`\T{signature }\NN{Semigroup}\:\{\\
\:\T{data } \\
\quad \NN{U}\\
\quad \NN{m} : \NN{U} \KO{\times} \NN{U} \to \NN{U}\\
\: \T{laws } \\
\quad \NN{assoc} ::
(\NN{m} \KO{\times} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\times} \NN{m}) \KO{;}\NN{m} \\
\}
`$
この書き方は、「指標と仕様」で述べた多パート指標〈multipart signature〉を実現するひとつの構文です。
指標により新規導入されて外部に公開される名前は二種類あります。
- 指標名〈signature name | name of signature〉: 指標自体の名前。上の例では $`\T{Semigroup}`$ 。指標が定義する代数系などの概念的事物の“種別の名前”でもある。
- 構成素役割り名〈constituent role name〉: 構造を構成する素材である構成素を識別する名前。上の例では $`\T{U}, \T{m}, \T{assoc}`$ 。モノの固有名でもないし、種別の名前でもない。構造〈組織体〉における役割りの名前。法則の名前も構成素役割り名。
ターゲット: 指標を解釈する場所
通常の解釈では、半群とは集合と関数から構成される構造です。そのことを指標に明示的に書くなら次のようです。
$`\T{signature }\NN{Semigroup}\:\{\\
\quad \NN{U} \In \KX{\bf Set}\\
\quad \NN{m} : \NN{U} \KO{\times} \NN{U} \to \NN{U} \In \KX{\bf Set}\\
\quad \NN{assoc} ::
(\NN{m} \KO{\times} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\times} \NN{m}) \KO{;}\NN{m} \In \KX{\bf Set}\\
\}
`$
ここで、名前 '$`{\bf Set}`$' は集合圏の固有名です。青色の名前なので既知名、つまり、集合圏については既によく知っているという前提で指標が書かれています。集合圏を知らないなら、この指標を解釈できません。
宣言の行ごとに $`\In {\bf Set}`$ と書くのが面倒なら、次のようにまとめて書いてもかまいません。
$`\T{signature }\NN{Semigroup}\:\T{within }\KX{\bf Set}\: \{\\
\quad \NN{U} \\
\quad \NN{m} : \NN{U} \KO{\times} \NN{U} \to \NN{U} \\
\quad \NN{assoc} ::
(\NN{m} \KO{\times} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\times} \NN{m}) \KO{;}\NN{m}\\
\}
`$
指標を解釈する場所となる圏をターゲット〈target | 標的環境〉と呼びます。上の半群の指標は、集合圏をターゲットとして解釈されます。
多くの場合ターゲットは圏です。ターゲット達が棲んでいる世界(例えば、デカルト圏達の2-圏)のほうはアンビエント〈ambient | 包囲環境〉と呼びます。ターゲットとアンビエントは混乱しがち(僕もたまに混乱します)ですが、別な概念です。
[/補足]
半群と同じ構造を別なターゲットにおいて解釈することができます。以下の指標は、事実上半群と同じですが、ターゲット(解釈の場)を実数係数ベクトル空間の圏 $`{\bf Vect}_{\bf R}`$ に指定しています。(習慣と気分により、モノイド積〈テンソル積〉の記号は '$`\otimes`$' に変えています。)
$`\T{signature }\NN{NonunitalAlgebra}\:\T{within }\KX{ {\bf Vect}_{\bf R} }\: \{\\
\quad \NN{U} \\
\quad \NN{m} : \NN{U} \KO{\otimes} \NN{U} \to \NN{U} \\
\quad \NN{assoc} ::
(\NN{m} \KO{\otimes} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\otimes} \NN{m}) \KO{;}\NN{m}\\
\}
`$
ベクトル空間の圏をターゲットとして解釈した半群相当の代数系は非単位的代数〈nonunital algebra〉と呼びます。
半群も非単位的代数もターゲットが違うだけで、公理系は共通です。ひとつの指標で記述できないでしょうか? 次のように書けばいいでしょう。
$`\T{variable }\VN{\cat{C}} \In \KX{\bf MonCAT}\\
\T{signature }\NN{NonunitalMonoid}\:\T{within }\VN{ \cat{C} }\: \{\\
\quad \NN{U} \\
\quad \NN{m} : \NN{U} \KO{\otimes} \NN{U} \to \NN{U} \\
\quad \NN{assoc} ::
(\NN{m} \KO{\otimes} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\otimes} \NN{m}) \KO{;}\NN{m}\\
\}
`$
薄紫色〈バイオレット〉の名前は変数名〈variable name〉です。変数の値は決まってませんが、型は決まっています。変数 $`\cat{C}`$ はモノイド圏(という型を持つ)変数です。モノイド圏達の2-圏を表す固有名 '$`{\bf MonCAT}`$' は既知の名前としています。変数は適当なタイミングで具体化〈instantiate〉できます。例えば、$`\cat{C} := {\bf Set}`$ と具体化すれば、
$`\quad \T{NonunitalMonoid}\:\T{within }{\bf Set}`$
は通常の半群〈semigroup〉のことです。一方、$`\cat{C} := {\bf Vect}_{\bf R}`$ と具体化すれば、
$`\quad \T{NonunitalMonoid}\:\T{within }{\bf Vect}_{\bf R}`$
は、実数係数の非単位的代数〈nonunital algebra〉です。
オレンジ色の新規名と薄紫色の変数名がどう違うかは後の節でさらに説明します。
別名と定義された名前
前節の半群の指標で、オレンジ色の新規名は、指標により導入されて外部に公開〈expose | advertize〉される名前です。'$`\T{U}`$'、'$`\T{m}`$' のような一文字の名前では短すぎる気がします。指標そのものを書き換えるテもありますが、より長い別名を定義してもいいでしょう。
$`\T{signature }\NN{Semigroup}\:\T{within }\KX{\bf Set}\: \{\\
\quad \NN{U} \\
\quad \NN{m} : \NN{U} \KO{\times} \NN{U} \to \NN{U} \\
\quad \NN{assoc} ::
(\NN{m} \KO{\times} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\times} \NN{m}) \KO{;}\NN{m}\\
\quad \T{alias }\NN{Carrier} := \NN{U}\\
\quad \T{alias }\NN{binOp} := \NN{m}\\
\}\\
\T{alias }\NN{Semi-Group} := \NN{Semigroup}\\
\T{alias }\NN{半群} := \NN{Semigroup}
`$
キーワード $`\T{alias}`$ で宣言された名前は、完全に同義語として扱われます。
- '$`\T{U}`$' という名前と '$`\T{Carrier}`$' という名前は何の違いもない。どちらを使うのも自由。
- '$`\T{m}`$' という名前と '$`\T{binOp}`$' という名前は何の違いもない。どちらを使うのも自由。
- '$`\T{Semigroup}`$' という名前と '$`\T{Semi-Group}`$' という名前と '$`\T{半群}`$' という名前は何の違いもない。どれを使うのも自由。
この指標から外部に公開される名前を列挙すると:
- $`\T{Semigroup}, \T{Semi-Group}, \T{半群}`$ (指標の名前、指標により定義される代数系の種別名)
- $`\T{U}, \T{Carrier}`$ (構成素の役割り名、日本語で言えば「台集合」)
- $`\T{m}, \T{binOp}`$ (構成素の役割り名、日本語で言えば「二項演算」)
- $`\T{assoc}`$ (構成素の役割り名、日本語で言えば「結合法則」)
指標のなかで、他の名前を使って新しい名前を定義してもかまいません。ここでの「定義」とは、別名ではなくて、違った意味でもよい名前を作り出すことです。例えば、次の指標のなかの $`\T{UPair}`$ は定義された名前〈defined name〉です。定義された名前も公開されます。
$`\T{signature }\NN{Semigroup}\:\T{within }\KX{\bf Set}\: \{\\
\quad \NN{U} \\
\quad \NN{UPair} := \NN{U} \KO{\times} \NN{U} \\
\quad \NN{m} : \NN{UPair} \to \NN{U} \\
\quad \NN{assoc} ::
(\NN{m} \KO{\times} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\times} \NN{m}) \KO{;}\NN{m}\\
\}
`$
名前を(宣言ではなくて)定義していることを強調したいなら、行頭にその旨を示すキーワードを付けるといいでしょう。例えば:
$`\quad \T{define }\NN{UPair} := \NN{U} \KO{\times} \NN{U}`$
変数名
指標に引数パラメータを持たせると便利なときがあります。非単位的モノイド〈nonunital monoid〉のターゲット圏を引数パラメータとして書くなら、例えば次のように書けます。
$`\T{signature }\NN{NonunitalMonoid}( \T{variable }\VN{\cat{C}} \In \KX{\bf MonCAT} )\: \{\\
\quad \NN{U} \In \VN{\cat{C}}\\
\quad \NN{m} : \NN{U} \KO{\otimes} \NN{U} \to \NN{U} \In \VN{\cat{C}} \\
\quad \NN{assoc} ::
(\NN{m} \KO{\otimes} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\otimes} \NN{m}) \KO{;}\NN{m} \In \VN{\cat{C}}\\
\}
`$
薄紫色の変数名が、オレンジ色の“新規導入され公開される名前”と違う点は、リネームしてもかまわないことです。例えば、上の指標の変数名 '$`\cat{C}`$' を '$`\cat{X}`$' にリネームしてみます。
$`\T{signature }\NN{NonunitalMonoid}( \T{variable }\VN{\cat{X}} \In \KX{\bf MonCAT} )\: \{\\
\quad \NN{U} \In \VN{\cat{X}}\\
\quad \NN{m} : \NN{U} \KO{\otimes} \NN{U} \to \NN{U} \In \VN{\cat{X}} \\
\quad \NN{assoc} ::
(\NN{m} \KO{\otimes} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\otimes} \NN{m}) \KO{;}\NN{m} \In \VN{\cat{X}}\\
\}
`$
リネームしても何も変わらないし、誰にも迷惑がかかりません。公開されているオレンジ色の名前をリネームしてしまうと問題が起きる可能性があります。
外部に公開はしたくない一時的な名前が欲しいときも、指標内で変数を宣言して、$`\T{let}`$ で束縛して使います。変数のスコープ〈通用範囲〉は限定されているので、使い捨ての名前になります。以下の指標の名前 '$`{P}`$' は使い捨ての変数名です。
$`\T{signature }\NN{Semigroup}\:\T{within }\KX{\bf Set}\: \{\\
\quad \NN{U} \\
\quad \T{variable }\VN{P}\\
\quad \T{let }\VN{P} := \NN{U} \KO{\times} \NN{U} \\
\quad \NN{m} : \VN{P} \to \NN{U} \\
\quad \NN{assoc} ::
(\NN{m} \KO{\times} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\times} \NN{m}) \KO{;}\NN{m}\\
\}
`$
代数系の指標を定義すると、その代数系の準同型射の指標は自動的に作れることが多いですが、明示的に準同型射の指標を手で書いてみます。半群の準同型射〈homomorphism〉の指標は以下のようです。引数パラメータを使っています。
$`\T{signature }\NN{SemigroupHom }(\\
\quad \T{variable }\VN{A} \T{ is }\KN{Semigroup}\\
\quad \T{variable }\VN{B} \T{ is }\KN{Semigroup}\\
)\:\{\\
\quad \T{datum } \NN{f} : \VN{A}.\KN{U} \to \VN{B}.\KN{U} \In \KX{\bf Set}\\
\quad \T{law }\NN{prsv-op} ::
\VN{A}.\KN{m} \KO{;} \NN{f} \twoto
(\NN{f} \KO{\times} \NN{f}) \KO{;} \VN{B}.\KN{m} \In \KX{\bf Set}\\
\quad \T{alias } \NN{演算の保存} := \NN{prsv-op}\\
\}
`$
この指標 $`\T{SemigroupHom}`$ が定義される時点では、名前 '$`\T{Semigroup}`$' や '$`\T{U}`$' は既知の名前となっているので青色です。この指標が使用している変数は $`A, B`$ (薄紫色)で、その型は $`\T{Semigroup}`$ です。キーワード $`\T{is}`$ と既に定義済みの指標名により、変数の型(変数名が指す予定のモノが何者であるかの情報)を宣言できます。
$`A.\T{U}`$ のようなドットを使った表現は「半群 $`A`$ の台集合」のように、構造の構成素を表す表現です。キーワード $`\T{datum}, \T{law}`$ を付けたのは、単なる気まぐれ(付けたい気分になった)です。
この指標が新規導入して外部に公開している名前は '$`\T{f}`$'、'$`\T{prsv-op}`$'、'$`\T{演算の保存}`$' です。$`\T{prsv-op}`$ は集合圏の等式なので、次の可換図式としても表示できます。
$`\quad \xymatrix {
{A.\T{U} \times A.\T{U}} \ar[r]^-{f\times f}
\ar[d]_{A.\T{m}}
& {B.\T{U} \times B.\T{U}} \ar[d]^{B.\T{m}}
\\
{A.\T{U}} \ar[r]_{f}
& {B.\T{U}}
}\\
\quad \text{commutative }\In {\bf Set}
`$
よくある記号の乱用(構造と台集合の意図的混同、演算名のオーバーロード)を認めるならば、次のように簡潔に書けます。
$`\quad \xymatrix {
{A \times A} \ar[r]^-{f\times f}
\ar[d]_{ \T{m} }
& { B \times B } \ar[d]^{\T{m}}
\\
{A} \ar[r]_{f}
& {B}
}\\
\quad \text{commutative }\In {\bf Set}
`$
純指標、構成手続き
この節は補足的な内容です。老婆心からの注意事項を述べます。
原則的に「指標は宣言の集まり」です。ひとつの宣言はひとつの名前を新規導入して外部に公開します。そうだとすると、次の行為は指標の任務から逸脱していると言えます。
- 公開する新しい名前の詳細・実体を定義する(宣言以上のことをする)。
- 公開しない名前、つまり変数名を使う。
- 公開しない名前、つまり変数名を新規導入する。
今まで挙げた例で言えば、次の行は公開する新しい名前の詳細・実体を定義しています。
$`\quad \NN{UPair} := \NN{U} \KO{\times} \NN{U}`$
'$`:=`$' という記号は、右辺により左辺の名前に意味を与えます。つまり、'$`:=`$' が、宣言(型の指定)以上の行為をしている証拠です。
名前を色分けしていたので、変数の使用や導入は、薄紫色の名前の出現ですぐにわかります。変数の使用/導入の例を再掲すると:
$`\T{variable }\VN{\cat{C}} \In \KX{\bf MonCAT}\\
\T{signature }\NN{NonunitalMonoid}\:\T{within }\VN{ \cat{C} }\: \{\\
\quad \cdots\\
\}
`$
$`\T{signature }\NN{NonunitalMonoid}( \T{variable }\VN{\cat{C}} \In \KX{\bf MonCAT} )\: \{\\
\quad \cdots\\
\}
`$
$`
\quad \T{variable }\VN{P}\\
\quad \T{let }\VN{P} := \NN{U} \KO{\times} \NN{U}
`$
$`\T{signature }\NN{SemigroupHom }(\\
\quad \T{variable }\VN{A} \T{ is }\KN{Semigroup}\\
\quad \T{variable }\VN{B} \T{ is }\KN{Semigroup}\\
)
`$
定義('$`:=`$' の出現で判別可能)や変数の使用/導入があると、与えられた素材から何かを作り出す(構成する)手順を記述していることになります。純粋な宣言の記述ではなくなります。
純粋な宣言の記述を純指標〈pure signature〉、作り方〈構成法〉の記述を構成手続き〈construction procedure〉と分けて考えたほうが理論的扱いはスッキリします。が、実際に使う場合は、純指標と構成手続きの境界は曖昧にして(広義の)「指標」と呼んでもいいだろうと思います。
指標の拡大: 差分記述
モノイドの指標は次のように書けます。
$`\T{signature }\NN{Monoid}\:\{\\
\quad \NN{U}\\
\quad \NN{m} : \NN{U} \KO{\times} \NN{U} \to \NN{U}\\
\quad \NN{e} : \KX{\bf 1} \to \NN{U}\\
\quad \NN{assoc} ::
(\NN{m} \KO{\times} \KX{\id}_{\NN{U}} ) \KO{;} \NN{m} \twoto
\KX{\alpha}_{\NN{U}, \NN{U}, \NN{U}} \KO{;} (\KX{\id}_{\NN{U}}\KO{\times} \NN{m}) \KO{;}\NN{m} \\
\quad \NN{lunit} ::
\KX{ {\lambda_{\NN{U}}}^{-1} } \KO{;} (\NN{e} \KO{\times} \KX{\id}_{ \NN{U} }) \KO{;} \NN{m} \twoto \KX{\id}_{\NN{U} } \\
\quad \NN{runit} ::
\KX{ {\rho_{\NN{U}}}^{-1} } \KO{;} (\KX{\id}_{\NN{U}} \KX{\times} \NN{e}) \KO{;} \NN{m} \twoto \KX{\id}_{\NN{U}} \\
\}
`$
青色の既知名として、幾つかの名前(記号)が出てきます。これらの意味と使用法は事前に知っていることを前提としています。
- $`{\bf 1}`$ : 集合圏(あるいは一般的なモノイド圏)の単位対象
- $`\lambda_{(\hyp)}`$ : 集合の直積(あるいは一般的なモノイド積)の左単位律子〈left unitor〉
- $`\rho_{(\hyp)}`$ : 集合の直積(あるいは一般的なモノイド積)の右単位律子〈right unitor〉
- $`{(\hyp)}^{-1}`$ : 写像(あるいは一般的な射)の逆〈inverse〉
等式〈2-射〉で記述されている法則 $`\T{lunit}, \T{runit}`$ を可換図式として描くなら次のようです。
$`\quad \xymatrix {
U \ar@{=}[r] \ar[d]_{ {\lambda_U}^{-1} }
& U \ar@{=}[dd]
\\
{ {\bf 1}\times U} \ar[d]_{e \times \id_U}
& {}
\\
{U\times U} \ar[r]^{m}
& U
}\\
\quad \text{commutative}
`$
$`\quad \xymatrix {
U \ar@{=}[r] \ar[d]_{ {\rho_U}^{-1} }
& U \ar@{=}[dd]
\\
{ U \times {\bf 1}} \ar[d]_{\id_U \times e }
& {}
\\
{U\times U} \ar[r]^{m}
& U
}\\
\quad \text{commutative}
`$
さて、半群の指標が既にあるなら、モノイドの指標はもっと短く書けます。半群の指標に足りない部分を書き足すことになります。
$`\T{signature }\NN{Monoid}\T{ extends }\KN{Semigroup}\:\{\\
\quad \NN{e} : \KX{\bf 1} \to \KN{U}\\
\quad \NN{lunit} ::
\KX{ {\lambda_{\KN{U}}}^{-1} } \KO{;} (\NN{e} \KO{\times} \KX{\id}_{ \KN{U} }) \KO{;} \KN{m} \twoto \KX{\id}_{\KN{U} } \\
\quad \NN{runit} ::
\KX{ {\rho_{\KN{U}}}^{-1} } \KO{;} (\KX{\id}_{\KN{U}} \KX{\times} \NN{e}) \KO{;} \KN{m} \twoto \KX{\id}_{\KN{U}} \\
\}
`$
モノイドの定義のときには半群の定義は済んでいるので、半群に関連する名前は既知の名前(青色で表示)になっています。モノイドの指標によって新たに導入され公開される名前は '$`\T{Monoid}`$'、'$`\T{e}`$'、'$`\T{lunit}`$'、'$`\T{runit}`$' です。
すぐ上のモノイドの指標のように、もとにする指標(今の場合は半群の指標)に書き足して作った指標は、もとの指標の拡大〈extension | 拡張〉と呼びます。指標の拡大を使うと、差分だけ記述すればよいので楽になるメリットがあります。それ以外にも指標の拡大には応用・活用があります*3。
中置演算子記号の宣言
2つの引数を持つ関数は、中置演算子記号〈infix operator symbol〉を使って書くことがよくあります。中置演算子記号も名前の一種ですが、通常の関数呼び出しとは別な構文になります。別名宣言〈alias宣言〉とは別な宣言で中置演算子記号を導入することにしましょう。
$`\T{signature }\NN{Monoid}\:\{\\
\quad \NN{U}\\
\quad \NN{m} : \NN{U} \KO{\times} \NN{U} \to \NN{U}\\
\quad \NN{e} : \KX{\bf 1} \to \NN{U}\\
\quad \T{notation } (\hyp \NX{*} \hyp) := \NN{m}(\hyp, \hyp)\\
\quad \T{notation } \NX{1} := \NN{e}\\
\quad \cdots \text{以下省略}\\
\}
`$
中置演算子記号の新規導入には、notation〈記法〉宣言を使うことにします。無名ラムダ変数(ハイフン記号)を使った単純な記述方式を採用します。
上記のnotation宣言で、中置演算子記号としてのアスタリスクと定数記号としての“数字のイチ”が新規導入され、外部に公開されます。アスタリスクや“数字のイチ”は、もちろん他の用途でも使われる名前なので、オーバーロード〈多義的使用〉になります。簡潔に書けるメリットと引き換えに、オーバーロードによるデメリットも発生します。
別名(別記法)としてではなくて、最初から演算子記号や数字の名前を宣言してもかまいません。記号を丸括弧で囲って、中置演算子記号であることを示します。
$`\T{signature }\NN{Monoid}\:\{\\
\quad \NN{U}\\
\quad (\NX{*}) : \NN{U} \KO{\times} \NN{U} \to \NN{U}\\
\quad \NX{1} : \KX{\bf 1} \to \NN{U}\\
\quad \cdots \text{以下省略}\\
\}
`$
名前依存性の色付き表示とグラフ表示
今まで、指標で新規導入された名前はオレンジ色にしてました。新規名の最初の出現だけをオレンジ色にして、それ以降は水色にすると次のようになります。
$`\newcommand{\LKN}[1]{ \textcolor{skyblue}{\text{#1}} } % Locally Known Name
\T{signature }\NN{Monoid}\:\{\\
\quad \NN{U}\\
\quad \NN{m} : \LKN{U} \KO{\times} \LKN{U} \to \LKN{U}\\
\quad \NN{e} : \KX{\bf 1} \to \LKN{U}\\
\quad \NN{assoc} ::
(\LKN{m} \KO{\times} \KX{\id}_{\LKN{U}} ) \KO{;} \LKN{m} \twoto
\KX{\alpha}_{\LKN{U}, \LKN{U}, \LKN{U}} \KO{;} (\KX{\id}_{\LKN{U}}\KO{\times} \LKN{m}) \KO{;}\LKN{m} \\
\quad \NN{lunit} ::
\KX{ {\lambda_{\LKN{U}}}^{-1} } \KO{;} (\LKN{e} \KO{\times} \KX{\id}_{ \LKN{U} }) \KO{;} \LKN{m} \twoto \KX{\id}_{\LKN{U} } \\
\quad \NN{runit} ::
\KX{ {\rho_{\LKN{U}}}^{-1} } \KO{;} (\KX{\id}_{\LKN{U}} \KX{\times} \LKN{e}) \KO{;} \LKN{m} \twoto \KX{\id}_{\LKN{U}} \\
\}
`$
指標名と、構成素役割り名の初出だけがオレンジ色です。上記のフォーマットなら、行の左端にオレンジ色の名前が並び、その他の部分はすべて青系(青色または水色)です。これは、下の行はそれより上(前)の行に依存してもよいが、逆向きの依存(その時点で未宣言な名前の使用)は出来ないということです。正体不明な名前がいきなり現れることはありません。
モノイドの指標内に現れる新規名のあいだの依存関係を有向グラフに描いてみましょう。次のようになります。
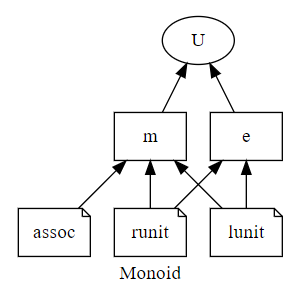
矢印の根本〈ねもと〉にある名前は、矢印の先にある名前に依存してます。直接矢印で結ばれてなくても、パス(矢印を繋げた有向折れ線)があれば依存性があります。矢印の先にある名前が宣言された後でないと、矢印の根本の名前は宣言できません。
グラフのノードの形状は次の約束です。
- sort(型/集合)を表す名前のノードはマル
- operation(演算/関数)を表す名前のノードは四角形
- equation(等式/法則)を表す名前のノードはメモ用紙〈note〉マーク
上記の名前依存性グラフは、Graphvizで描いて、スクリーンショット画像にしたものです。Graphvizのdot言語ソースは以下のとおりです。
digraph { label="Monoid" rankdir=BT U m[shape=box] e[shape=box] m -> U e -> U assoc[shape=note] lunit[shape=note] runit[shape=note] assoc -> m lunit -> m lunit -> e runit -> m runit -> e }
指標拡大〈signature extension〉も有向グラフに描くと分かりやすいです。以下のグラフは、半群の指標と、それを拡大〈extend | 拡張〉したモノイドの指標の関係を表しています。
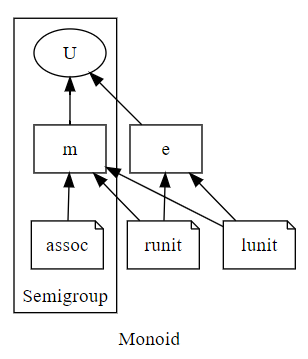
digraph { label="Monoid" rankdir=BT subgraph cluster_0 { label="Semigroup" U m[shape=box] m -> U assoc[shape=note] assoc -> m } e[shape=box] e -> U lunit[shape=note] runit[shape=note] lunit -> m lunit -> e runit -> m runit -> e }
もうひとつ、モノイドの指標を“データ〈data〉パート”と“法則〈laws〉パート”に分けたときの、パート分けを描くと次のようです。
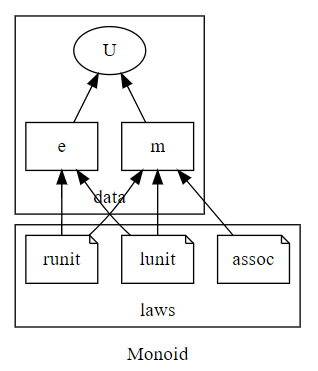
digraph { label="Monoid" rankdir=BT subgraph cluster_0 { label="data" U m[shape=box] e[shape=box] m -> U e -> U } subgraph cluster_1 { label="laws" assoc[shape=note] lunit[shape=note] runit[shape=note] assoc -> m lunit -> m lunit -> e runit -> m runit -> e } }
指標に出現する名前達の相互関係やグルーピングを視覚化〈visualize〉すると、指標の構文論的/意味論的構造が理解しやすくなります。
図式による法則の記述
等式による法則〈equational law〉は、テキスト数式で書くより、可換図式に描いたほうが分かりやすいです。特に、高次元の圏類似代数系〈category-like algebraic {system | structure}〉になると、テキスト記述は困難になります。図式による記述を積極的に取り入れましょう*4。
既に、半群/モノイドの等式的法則を可換図式でも表示しています。可換図式はペースティング図の特別なものです。以下では、ペースティング図としての可換図式の描き方を説明します。
まず、以下のような四辺形があったとします(四辺形と四角形の違いは「圏論におけるフレーム充填問題 // n辺形とn角形」参照)。
$`\quad \xymatrix {
A \ar[d]_{f} \ar[r]^{p}
& B \ar[d]^{g}
\\
X \ar[r]_{q}
& Y
}`$
上記の四辺形(1次元図形)を境界として、内部を埋めた四角形〈2-射 | 2次元セル〉を $`\alpha`$ とするとき、次のように描きます。
$`\quad \xymatrix {
A \ar[d]_{f} \ar[r]^{p}
\ar@{}[dr]|{\alpha}
& B \ar[d]^{g}
\\
X \ar[r]_{q}
& Y
}`$
2-射 $`\alpha`$ が等式〈恒等2-射〉であるとき、そのことを示すために左側にイコール記号を注釈します。
$`\quad \xymatrix {
A \ar[d]_{f} \ar[r]^{p}
\ar@{}[dr]|{=\, \alpha}
& B \ar[d]^{g}
\\
X \ar[r]_{q}
& Y
}`$
これは、テキスト等式に書き下せますが、$`f;q`$ を左辺としたい旨を表すために斜め矢印も添えます。
$`\quad \xymatrix {
A \ar[d]_{f} \ar[r]^{p}
\ar@{}[dr]|{\underset{\nearrow}{=}\, \alpha}
& B \ar[d]^{g}
\\
X \ar[r]_{q}
& Y
}`$
この図式は、次のテキスト等式(ただし、イコールに二重矢印を使用)に対応します。
$`\quad \alpha :: f;q \twoto p;g : A \to Y`$
等式なら、左辺と右辺を交換できますが、一般的な2-射ではそうもいきません。一般論としては、斜め矢印は必須です。$`p;g`$ を左辺にしたいなら次の斜め矢印を添えます。
$`\quad \xymatrix {
A \ar[d]_{f} \ar[r]^{p}
\ar@{}[dr]|{\underset{\swarrow}{=}\, \alpha}
& B \ar[d]^{g}
\\
X \ar[r]_{q}
& Y
}`$
これは、次のテキスト等式に対応します。
$`\quad \alpha :: p;g \twoto f;q : A \to Y`$
今紹介した描き方で、モノイドの結合法則と左単位法則を描いてみます。
$`\quad \xymatrix{
(U\times U)\times U \ar[r]^{\alpha_{U,U,U}} \ar[d]_{m\times \id_U}
\ar@{}[ddr]|{\underset{\nearrow}{=}\,\T{assoc}}
& U\times (U \times U) \ar[d]^{\id_U \times m}
\\
U\times U \ar[d]_{m}
& U\times U \ar[d]^{m}
\\
U \ar@{=}[r]
& U
}\\
\quad \In {\bf Set}
`$
$`\quad \xymatrix @C+1.5pc{
U \ar@{=}[r] \ar[d]_{ {\lambda_U}^{-1} }
\ar@{}[ddr]|{\underset{\nearrow}{=}\, \T{lunit}}
& U \ar@{=}[dd]
\\
{ {\bf 1}\times U} \ar[d]_{e \times \id_U}
& {}
\\
{U\times U} \ar[r]^{m}
& U
}\\
\quad \In {\bf Set}
`$
これらはそれぞれ、以下のテキスト等式に対応します。
$`\quad \T{assoc} :: (m\times \id_U) ; m \twoto \alpha_{U,U,U} ; (\id_U \times m); m\\
\qquad : (U\times U)\times U \to U \In {\bf Set}\\
\quad \T{lunit} :: {\lambda_U}^{-1}; (e \times \id_U) ; m \twoto \id_U : U \to U
\In {\bf Set}
`$
四角形の内部のラベルを2-射の名前だと解釈することが肝要です。境界四辺形に対して2-射の膜が張っているイメージです。等式も四角形の内部に張る膜です。
そしてそれから
以上で、指標と名前の基本的なことは説明できたと思います。応用編として続きの記事を書く予定ではいますが、もう色は付けないかなぁ。だって、色付けるの手でやってるからめんどくさいんだもん。色が付いてなくても、名前の種類や用法を判別できるようになってくださいな。
*1:色もフォントも揃えようと思えば出来るのですが、ちょっとめんどくさくて‥。
*2:名前の細かい種別は、多くの場合、名前を圏のk-射と解釈したときの次元 k です。二重圏では、1-射がさらにタイト1-射、プロ1-射に分類されます。「二重圏、縦横をもう一度」参照。
*3:指標拡大は、構文付き変換手インスティチューション(「構文付き変換手インスティチューション 1/n」参照)では、非常に重要です。
*4:僕は、テキストによる記述は“必要悪”だと捉えています。「「コミュニケーションの多次元化」という革命に立ち会っているのだと思う」参照。