ここ2,3年「二重圏がきてる」印象があります。応用圏論を牽引している一人であるイバン・パターソン〈Evan Patterson〉は今年の1月、トポス・インスティチュートのブログ記事に次のように書いています。
Lately I’ve been fixated on double categories, pursuing a range of theoretical and applied directions.
最近、私は二重圏に魅入られており、理論および応用の様々な方向性を幅広く追求しています。
パターソンの記事は、二重圏について紹介・解説するシリーズの一回目です。
- Title: Why double categories? Part 1
- Author: Evan Patterson
- Date: 2024-01-15
- URL: https://topos.site/blog/2024-01-15-why-double-categories-part-1
二重圏に可能性を感じる人はパターソンだけではありません。2022年に行われたワークショップの資料・録画が次のページに残っています。
様々な場面で二重圏が有効に使えることが伺えます。
ところが、用語法が不安定なので、二重圏を語るのは難しい面があります。以前、次の記事を書きました。
二重圏の定義と呼び名を書いているだけです。今回もまた定義と呼び名の話で、過去記事に補足をします。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\dcat}[1]{\mathbb{#1}}
\newcommand{\hyp}{\text{-} }
\newcommand{\NFProd}[3]{ \mathop{_{#1} \!\underset{#2}{\times}\,\!_{#3} } }
`$
内容:
プロ射は縦射か横射か?
二重圏は、0次元、1次元、2次元の射を持ちます。0次元の射は対象〈object〉です。2次元の射は2-射〈2-morphism〉、2-セル〈2-cell〉、二重射〈doublemorphism〉*1などと呼ばれます。問題は1次元の射です。1次元の射はニ種類あり、片方はプロ射〈proarrow | promorphism〉と呼ばれます。プロ射でないほうの1-射は単に「射」とも呼ばれますが、「射」は一般的過ぎます。
ナタニエル・アーカーとディラン・マクダルメットは、次の論文で「タイト」と「ルーズ」という形容詞を使っています。
- [AM23]
- Title: The formal theory of relative monads
- Authors: Nathanael Arkor, Dylan McDermott
- Submitted: 27 Feb 2023 (v1), 17 May 2023 (v2)
- Pages: 85p
- URL: https://arxiv.org/abs/2302.14014
タイト射(タイトな1-セル)は“プロ射ではない1-射”の意味です。ここでは、二重圏のニ種類の1-射を(バランスが悪いのですが)、タイト射〈tight {morphism | arrow}〉とプロ射とします。「プロ射」は広く合意された用語なので捨てたくないのです。
ほとんどの人は、タイト射とプロ射を縦横で区別しています。困ったことに、縦横の使い方が人により違います。
nLabは、圏論関係用語の基準として採用されることが多いですが、nLab項目https://ncatlab.org/nlab/show/double+categoryでは、プロ射が横射です。
上記のアーカー/マクダルメット論文は、「縦横」を使わないように配慮してますが、ペースティング図ではプロ射が横射です。
しかし、プロ射を縦射にとる人もいます。しばしば参照されるマルコ・グランディやロバート・パレの論文では、プロ射が縦射です。
- [GP99]
- Title: Limits in double categories
- Authors: Marco Grandis, Robert Pare
- Date: 1999
- Pages: 60p
- URL: http://www.numdam.org/item/CTGDC_1999__40_3_162_0/
- [Par11]
- Title: Yoneda theory for double categories
- Author: Robert Paré
- Date: 2011
- Pages: 55p
- URL: http://www.tac.mta.ca/tac/volumes/25/17/25-17abs.html
昔から二重圏にたずさわっている人が「プロ射が縦射」を使う印象(単に印象です)があるので、「プロ射が縦射」方式を伝統派と呼んでおきましょう。最近でも、伝統派用語法は使われています。
クラウディオ・ピザニ(2022年 プロ射が縦射):
- [Pis22-]
- Title: Operads as double functors
- Author: Claudio Pisani
- Submitted: 15 Aug 2022
- Pages: 14p
- URL: https://arxiv.org/abs/2208.07028
リン・モイザー/マル・サラソラ/パウラ・ヴェルデュゴ(2020年 プロ射が縦射):
- [MSV20-21]
- Title: A 2Cat-inspired model structure for double categories
- Authors: Lyne Moser, Maru Sarazola, Paula Verdugo
- Submitted: 29 Apr 2020 (v1), 1 May 2021 (v5)
- Pages: 42p
- URL: https://arxiv.org/abs/2004.14233
ディビッド・ジャズ・マイヤースは、ペースティング図ではプロ射を縦にとっています。ストリング図にすると、ポアンカレ双対でプロ射が横方向のワイヤーになります。ストリング図ワイヤーとして横方向に描かれたプロ射を、マイヤースは「横射」と呼んでいます。結果的にプロ射が横射です。
- [Mye16-18]
- Title: String Diagrams For Double Categories and Equipments
- Author: David Jaz Myers
- Submitted: 8 Dec 2016 (v1), 2 Mar 2018 (v4)
- Pages: 33p
- URL: https://arxiv.org/abs/1612.02762
階付き構造としての二重圏
二重圏を白抜き黒板文字で表すことが多いので、この習慣に従います。「二重圏を語るために」で述べたように、二重圏は 0, 1, 2 で階付け〈grading〉された圏達と関手達からなります。それを次の図で表します。
$`\quad \xymatrix@C+1pc{
\dcat{D}_0 \ar[r]
& \dcat{D}_1 \ar@/^1pc/[l] \ar@/_1pc/[l]
& \dcat{D}_2 \ar[l]
} \In {\bf CAT}`$
$`\dcat{D}_2`$ も圏ですが、圏としての結合と恒等には興味がなくて、圏の下部構造であるグラフしか使いません。グラフとしての $`\dcat{D}_2`$ は、$`\dcat{D}_0, \dcat{D}_1`$ からファイバー積として作られます*2。この事情も記入すると次のようになります。
$`\quad \xymatrix@C+1pc{
\dcat{D}_0 \ar[r]^{\mrm{unit}}
& \dcat{D}_1 \ar@/^1pc/[l]^{\mrm{trg}} \ar@/_1pc/[l]_{\mrm{src} }
& \dcat{D}_2 \ar[l]_{\mrm{prod}}
} \In {\bf CAT}\\
\text{Where}\\
\quad \dcat{D}_2 = \dcat{D}_1 \NFProd{\mrm{trg}}{\dcat{D}_0}{\mrm{src}} \dcat{D}_1
`$
$`\dcat{D}_0, \dcat{D}_1`$ は二重圏の構成素です。構成素の役割り名として0階の圏〈category of grade 0〉、1階の圏〈category of grade 1〉と呼ぶことにします。圏対象〈内部圏〉としては、圏対象の“対象対象”と圏対象の“射対象”ですが、ちょっと分かりにくいので0階・1階を使います。
$`\dcat{D}_0, \dcat{D}_1`$ はそれぞれ圏なので、その圏構造を次のように表します。
$`\quad \dcat{D}_0 = (|\dcat{D}_0|_0, |\dcat{D}_0|_1, \mrm{dom}, \mrm{cod}, \mrm{id}, \mrm{comp} )\\
\quad \dcat{D}_1 = (|\dcat{D}_1|_0, |\dcat{D}_1|_1, \mrm{Dom}, \mrm{Cod}, \mrm{Id}, \mrm{Comp} )
`$
ここで、$`|\hyp|_0`$ は圏の対象の集合、$`|\hyp|_1`$ は圏の射の集合です。0階の圏の構成素名は一律に小文字始まり、0階の圏の構成素名は一律に大文字始まりとしました。
構成素であるそれぞれの圏が持っている圏構造以外に、0階・1階・2階の圏達(2階の圏構造は興味ないが)が作る圏構造があります。
$`\quad \dcat{D} = (\dcat{D}_0, \dcat{D}_1, \mrm{src}, \mrm{trg}, \mrm{unit}, \mrm{prod} )`$
ここで、$`\mrm{src}, \mrm{trg}, \mrm{unit}, \mrm{prod}`$ は写像ではなくて関手です。src は source の短縮、trg は target の短縮、prod は product の短縮です。unit, prod を使ったのは、二重圏の特殊ケースであるモノイド圏を考えたときの単位対象〈unit object〉、モノイド積〈monoidal product〉に対応するからです*3。
構成素であるそれぞれの圏を“内部圏”、3つの圏が作る圏を“外部圏”と呼ぶと分かりやすそうなんですが、二重圏全体が内部圏〈圏対象〉なので、かえって混乱してしまいます。それでも、$`\mrm{prod}`$ を外部結合〈external composition〉と呼ぶことはあるようです。
ここでは、関手達 $`\mrm{src}, \mrm{trg}, \mrm{unit}, \mrm{prod}`$ で構成される圏構造は(二重圏の)全体圏〈entire category〉と呼ぶことにします。
以上に定義した呼び名は縦横を使ってないので、いわば方向中立です。描画法の縦横を決めているときは、縦横を使ったほうが便利なので、方向中立な呼び名から方向(縦横)を使った呼び名に変更することになります。その例を次節で挙げます。
縦横を使う
「二重圏の語法・記法、ローカルルール事例」で述べた縦横を使った用語・記法を、方向中立な場合との対応表を作ってみましょう。下に、ペースティング図とストリング図があります。
| 方向中立 | 縦横を使った場合の事例 |
|---|---|
| 0階の圏の対象 | 対象、ラテン文字大文字 |
| 0階の圏の射 | 縦射または射、ラテン文字小文字 |
| 0階の圏の域割り当て | 縦射の域(対象) |
| 0階の圏の余域割り当て | 縦射の余域(対象) |
| 0階の圏の恒等割り当て | $`\mrm{vid}`$ 、恒等縦射(縦のイコール) |
| 0階の圏の結合 | $`;`$ 、縦射の縦結合または結合 |
| 1階の圏の対象 | 横射またはプロ射、ラテン文字大文字 |
| 1階の圏の射 | 2-射、ギリシャ文字小文字 |
| 1階の圏の域割り当て | 2-射のソース(上境界線) |
| 1階の圏の余域割り当て | 2-射のターゲット(下境界線) |
| 1階の圏の恒等割り当て | $`\mrm{vId}`$ 、縦結合恒等2-射(2次元) |
| 1階の圏の結合 | $`;`$ 、2-射の縦結合 |
| 全体圏の域割り当て | 2-射の左フレーム(左境界線) |
| 全体圏の余域割り当て | 2-射の右フレーム(右境界線) |
| 全体圏の恒等割り当て 対象パート | $`\mrm{hid}`$ 、恒等横射(横のイコール) |
| 全体圏の恒等割り当て 射パート | $`\mrm{hId}`$ 、横結合恒等2-射(2次元) |
| 全体圏の結合 | $`*`$ 、横結合(横射と二重射でオーバーロード) |
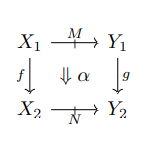
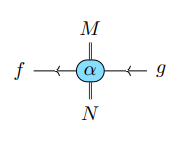
ほんとに標準はないので、毎回このような対応表を作る必要があります。ペースティング図では、縦方向は上から下、横方向は左から右が大部分ですが、ストリング図は下から上や右から左もありますから、ワイヤーの上下左右にも注意が必要です。慣れればさほどの事でもないのですが、最初は混乱しがちです(「双対や随伴に強くなるためのトレーニング」参照)。
二重圏は役に立つ構造なのですが、定義・用語・記法がゴチャゴチャしていてスタートで躓いてしまう懸念があるので、再度、縦横について整理してみました。