フレーム充填問題(「圏論におけるフレーム充填問題」参照)の解の全体、つまり解空間は、ファイバー付き圏のバンドルになります。フレーム充填問題のフレーム付き指標は、フレーム条件にファイバー付き圏のバンドルを対応させる関手を定義します。このことを取り急ぎザッっと説明します。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\op}{ \mathrm{op} }
\newcommand{\In}{\text{ in }}
%\newcommand{\dimU}[2]{ {{#1}\!\updownarrow^{#2}} }
\newcommand{\Imp}{\Rightarrow}
\newcommand{\u}[1]{\underline{#1}}
%\newcommand{\o}[1]{\overline{#1}}
\newcommand{\twoto}{ \Rightarrow }
%\newcommand{\id}{ \mathrm{id} }
\newcommand{\hyp}{\text{-} }
%\newcommand{\NFProd}[3]{ \mathop{_{#1} \!\underset{#2}{ \times }\,\!_{#3} } }
\newcommand{\T}[1]{\text{#1} }
%%
\newcommand{\epito}{\twoheadrightarrow}
%\newcommand{\monoto}{\rightarrowtail}
\newcommand{\incto}{\hookrightarrow}
%%
\require{color} % Using
%\newcommand{\NN}[1]{ \textcolor{orange}{\text{#1}} } % New Name
`$
内容:
相対指標
ここでの指標〈具象指標〉とは「等式的2-グラフ(2-圏の記述のために)」で述べた等式的2-グラフのことだとします。等式的2-グラフの特別なものとして、2-グラフや等式的1-グラフ、1-グラフなども含みます。これらをひっくるめて指標〈具象指標〉と呼ぶことにします。
指標 $`\Sigma`$ が指標 $`\Sigma'`$ の部分指標〈subsignature〉であるとは、次のことです。
- $`k = 0, 1, 2, 3`$ に対して、$`|\Sigma|_k \subseteq |\Sigma'|_k`$
- $`\Sigma`$ の面写像〈face maps〉は、$`\Sigma'`$ の面写像の制限になっている。
指標 $`\Sigma`$ が指標 $`\Sigma'`$ の部分指標であることを、集合の包含関係の記号をそのまま使って次のように書きます。
$`\quad \Sigma \subseteq \Sigma'`$
指標 $`\Sigma'`$ とその部分指標とのペア $`(\Sigma , \Sigma')`$ を相対指標〈relative signature〉と呼びます。相対指標のペアは、それとわかるように $`(\Sigma \subseteq \Sigma')`$ と書くことにします。
相対指標を具体的に描くときは、部分指標に(黒以外の)色を付けることにします。例えば、プルバックを定義するための相対指標は次のようになります。図の描き方は「構造記述のための指標と名前 1/n 基本 // 図式による法則の記述」を参照してください。
$`\quad \xymatrix{
\cdot \ar[r] \ar[d]
\ar@{}[dr]|{\underset{\nearrow}{=} }
& \textcolor{red}{\cdot} \ar@[red][d]
\\
\textcolor{red}{\cdot} \ar@[red][r]
& \textcolor{red}{\cdot}
}`$
頂点と辺にラベルを付けてテキスト表示すると次のようになります。
$`\T{signature } \{\\
\quad X\\
\quad \textcolor{red}{A, B, C}\\
\quad \textcolor{red}{ f: A \to C}\\
\quad \textcolor{red}{ g: B \to C}\\
\quad p : X \to \textcolor{red}{A}\\
\quad q : X \to \textcolor{red}{B}\\
\quad \alpha :: p;\textcolor{red}{f} \overset{=}{\twoto} q; \textcolor{red}{g}\\
\}`$
赤い部分が部分指標です。$`\alpha`$ は2-射ですが、二重矢印の上のイコール記号が、恒等2-射(1-射のあいだの等式)であることを示しています。
毎回色を付けるのも面倒なので、指標の拡大〈拡張 | extension〉(「構造記述のための指標と名前 1/n 基本 // 指標の拡大: 差分記述」参照)を利用して相対指標を書いてもいいとします。
$`\T{signature } \T{Red} \:\{\\
\quad {A, B, C}\\
\quad {f: A \to C}\\
\quad {g: B \to C}\\
\}\\
\T{signature }\hyp \T{ extends }\T{Red}\:\{\\
\quad X\\
\quad p : X \to {A}\\
\quad q : X \to {B}\\
\quad \alpha :: p;{f} \overset{=}{\twoto} q; {g}\\
\}`$
$`\T{Red}`$ が部分指標で、それを拡大した無名(名前がハイフン)な指標が全体指標です。出現する名前〈ラベル〉のあいだの名前依存性グラフ(「構造記述のための指標と名前 1/n 基本 // 名前依存性の色付き表示とグラフ表示」参照)は以下のようです*1。
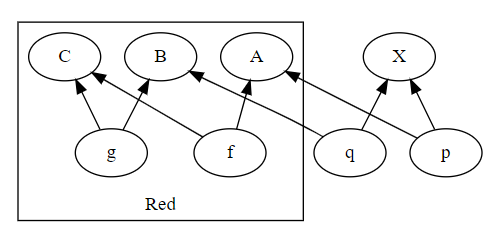
相対指標を $`\Sigma`$ と一文字で書いたときは、部分指標を $`\Sigma_0`$ 、全体指標を $`\Sigma_1`$ とします。つまり:
$`\quad \Sigma = (\Sigma_0 \subseteq \Sigma_1)`$
以下、$`\Sigma, \Gamma`$ は相対指標で、$`\Phi,\Psi`$ は単独の指標だとします。単独の指標 $`\Phi`$ から相対指標を作る自明な方法が2つあります。
$`\quad (\emptyset \subseteq \Phi)\\
\quad (\Phi \subseteq \Phi)
`$
$`\emptyset`$ は、すべての次元のセル集合が空である空指標です。
指標のモデル
$`\cat{K}`$ を厳密2-圏とします。$`\cat{K}`$ の3-射とは、2-射のあいだの等式のことだとします。2-圏の結合演算(横結合と縦結合)と恒等射(0-射の恒等1-射と1-射の恒等2-射)の割り当てを忘却すると、2-圏は等式的2-グラフになります。その忘却関手は $`\mathbb{U}_2`$ とします(「等式的2-グラフ(2-圏の記述のために) // グラフの随伴系とモナド」参照)。
$`\quad \mathbb{U}_2 : {_1{\bf s2CAT}^\mrm{str}} \to {\bf Eq2GRAPH} \In \mathbb{CAT}\\
\qquad |{_1{\bf s2CAT}^\mrm{str}}|\ni \cat{K} \mapsto \mathbb{U}_2(\cat{K}) \;\in |{\bf Eq2GRAPH}|
`$
ここで:
- $`{\bf s2CAT}`$ : 大きい〈必ずしも小さくない〉厳密2-圏達からなるとても大きな3-圏
- $`{_1{\bf s2CAT}}`$ : 大きい〈必ずしも小さくない〉厳密2-圏達からなるとても大きな1圏(3-圏の切り落とし)
- $`{_1{\bf s2CAT}^\mrm{str}}`$ : 大きい〈必ずしも小さくない〉厳密2-圏のあいだの射を厳密2-関手に限定したとても大きな1圏
- $`{\bf Eq2GRAPH}`$ : 大きい〈必ずしも小さくない〉等式的2-グラフからなる1-圏
- $`\cat{K}`$ : 大きい〈必ずしも小さくない〉2-圏、例えば $`\cat{K} = {\bf Cat}`$
厳密2-圏達の圏 $`{\bf s2CAT}`$ は3-圏ですが、2-射(0-変換手のあいだの1-変換手)と3-射(1-変換手のあいだの2-変換手)を捨てて1-圏とみなしたものが $`{_1{\bf s2CAT}}`$ です。さらに、$`{_1{\bf s2CAT}^\mrm{str}}`$ では厳密2-関手だけしか考えてないので、もとの3-圏から多くのモノを捨てています。捨て過ぎかも知れませんが、議論は単純になります。対象〈0-射〉は捨ててないので次が成立します。
$`\quad |{\bf s2CAT}| = |{_1{\bf s2CAT}}| = |{_1{\bf s2CAT}^\mrm{str}}|`$
大文字の名前を使っているのは、サイズが1レベル大きいことを示します。$`\cat{K} = {\bf Cat}`$ の場合、
$`\quad {\bf Cat} \not\in |{\bf s2Cat}|`$
ですが、
$`\quad {\bf Cat} \in |{\bf s2CAT}|`$
となります。
指標(等式的2-グラフ) $`\Phi`$ の$`\cat{K}`$-ターゲット・モデル〈$`\cat{K}`$-targeted model〉とは、次のような指標射(等式的2-グラフの射)です。
$`\quad m : \Phi \to \mathbb{U}_2(\cat{K}) \In {\bf Eq2GRAPH}`$
等式的2-グラフのあいだの射〈準同型射〉については、「等式的2-グラフ(2-圏の記述のために)」で述べてませんが、各次元のセルのあいだの写像であって、面写像を(厳密に)保存するものが等式的2-グラフの射〈morphism between equational 2-graphs〉です。
例えば、$`\Phi`$ が、「等式的2-グラフ(2-圏の記述のために)」で事例として出したモナドの指標で、ターゲットが $`\cat{K} = {\bf Cat}`$ ならば、モデル $`m`$ は小さい圏上のモナドです。
自由-忘却・随伴ペア $`\mathbb{Free}_2 \dashv \mathbb{U}_2`$ があるので、そのホムセット同型から、$`m`$ に対応する $`m'`$ があります。
$`\quad m' : \mathbb{Free}_2(\Phi) \to \cat{K} \In {_1{\bf s2CAT}^\mrm{str}}`$
随伴に伴うホムセット同型(転置/反転置)で対応する $`m,m'`$ はしばしば同一視され、どちらも(指標の)モデルと呼びます。
$`\quad {_1{\bf s2CAT}^\mrm{str}}(\mathbb{Free}_2(\Phi), \cat{K}) \ni m'
\longleftrightarrow m \in
{\bf Eq2GRAPH}(\Phi, \mathbb{U}_2(\cat{K}))
`$
モデル全体の集合/圏は、ホムセット/ホム圏として定義します。一般には、厳密2-圏のあいだの関手でも、ラックス2-関手やスード関手を考えることができますが、ここでは、厳密2-関手に限定しています。モデル空間(1-圏になる)は次のように定義します。
$`\quad {\mrm{Model}}(\Phi, \cat{K}) := {_1 [\mathbb{Free}_2(\Phi), \cat{K}]_1^\mrm{str}}
= {_1{\bf s2CAT}^\mrm{str}}(\mathbb{Free}_2(\Phi), \cat{K}) \; \in |{\bf CAT}|
`$
ここで使っているブラケット記法については「変換手意味論とブラケット記法」を参照してください。このモデル圏の定義は、通常の関手意味論の方法を適用したことになります。
1-圏の枠組みに収めるために、3-圏 $`{\bf s2CAT}`$ の高次の部分(2-射と3-射)や厳密ではない緩い〈弱い〉1-射は全部捨てる方針を採用しました。これが限定的過ぎる方針なのは承知ですが、簡単なケースから始めたいので。
フレーム充填問題
「圏論におけるフレーム充填問題」で述べたフレーム充填問題を、相対指標を使って定式化します。
フレーム充填問題の文脈においては、相対指標 $`(\Sigma_0\subseteq \Sigma1)`$ の部分指標 $`\Sigma_0`$ をフレーム〈frame〉と呼びます。「圏論におけるフレーム充填問題」においては、「フレームは境界の一部だ」と言いましたが、部分指標なら何でもいいとします。例えば、フレームが全体指標〈total signature〉 $`\Sigma_1`$ と一致してしまうケース $`(\Sigma_1, \Sigma_1)`$ も許します。フレームが空でもかまいません。
フレーム充填問題の文脈においては、問題を記述する相対指標をフレーム付き指標〈framed signature〉とも呼ぶことにします。
- $`(\Sigma_0, \Sigma_1)`$ : フレーム充填問題の、フレーム付き指標
- $`\Sigma_1`$ : フレーム充填問題の、全体指標
- $`\Sigma_0`$ : フレーム充填問題の、フレーム
フレーム付き指標 $`(\Sigma_0, \Sigma_1)`$ に対して、フレーム〈部分指標〉$`\Sigma_0`$ の(適当なターゲットの)モデルを、フレーム条件〈frame condition〉と呼びます(後で一般的な定式化をします)。
具体例を出しましょう。相対指標 $`(\Sigma_0, \Sigma_1)`$ として、先のプルバックの相対指標(以下に再掲)を考えます。
$`\quad \xymatrix{
\cdot \ar[r] \ar[d]
\ar@{}[dr]|{\underset{\nearrow}{=} }
& \textcolor{red}{\cdot} \ar@[red][d]
\\
\textcolor{red}{\cdot} \ar@[red][r]
& \textcolor{red}{\cdot}
}`$
赤い部分がフレームです。このように、(何らかの方法で)フレームが指定された指標〈等式的2-グラフ〉がフレーム充填問題のフレーム付き指標です。
モデルのターゲットとして、小さい圏達の2-圏 $`{\bf Cat}\in |{\bf s2CAT}|`$ を考えます(小さい圏達の2-圏は大きい2-圏なので、とても大きい3-圏の対象)。フレーム条件とは、フレームであるコスパンを2-圏 $`{\bf Cat}`$ 内に描出〈rendering〉した図式〈diagram〉です。コスパン形状の頂点と辺に、実際の圏と関手が割り当てられます。
$`\quad \xymatrix{
{}
& \textcolor{red}{\cat{B}} \ar@[red][d]^{\textcolor{red}{G} }
\\
\textcolor{red}{\cat{A}} \ar@[red][r]_{\textcolor{red}{F} }
& \textcolor{red}{\cat{C} }
}\\
\quad \In {\bf Cat}
`$
相対指標のフレーム部分は“決まっている”状態になります。しかし、フレーム以外の部分は“決まってない”ままです。フレーム付き指標〈相対指標〉とフレーム条件(フレーム上のモデル)が、フレーム充填問題〈frame filling problem〉そのものです。
フレーム充填問題の解〈solution〉またはフィラー〈filler〉とは、全体指標のモデルで、フレーム部分ではフレーム条件に一致するものです。言い方を変えると、フレーム充填問題の“決まってない”部分を全部決めたモデルが解〈フィラー〉です。
今の具体例で言えば、“決まってない”部分は:
- 0-射〈対象 | 圏〉が1つ
- 1-射〈関手〉が2つ
- 2-射(ただし、恒等1-射=等式〉が1つ
具体例の解〈フィラー〉がただちにプルバック図式というわけではありません。解は単に可換図式なだけであって、極限を定義しているとは限りません。解の全体を圏とみなしたときの終対象がプルバック図式です。
与えられたフレーム付き指標とフレーム条件に対して、フレーム以外の部分を埋めるので、フレーム充填というより(フレームは既に埋まっているので)フレーム以外を充填ですね。行きがかり上、フレーム充填問題と(少なくても当面は)呼びますが*2。
ファイバー付きモデル空間関手
「空間」という言葉は、「変換手意味論とブラケット記法 // 「空間」という言葉」で説明した用法で使います。集合でも圏でも2-圏でも、モノの集まりは、構造があろうがなかろうが何でも「空間」と呼べます*3。
前々節「指標のモデル」で定義したモデル空間は、次のようでした。
$`\quad \mrm{Model}(\Phi, \cat{K}) := {_1 [\mathbb{Free}_2(\Phi), \cat{K}]_1^\mrm{str}} \;\in |{\bf CAT}|
`$
ターゲット $`\cat{K}`$ を固定しているときは、$`\mrm{Model}_\cat{K}(\hyp )`$ の形も使います。さらに、ターゲット $`\cat{K}`$ が文脈から明らかなら $`\mrm{Model}(\hyp)`$ と略記します。ここからは、ターゲットを $`{\bf Cat}`$ に固定して、$`\mrm{Model}(\hyp) = \mrm{Model}_{\bf Cat}(\hyp)`$ とします。
“指標/指標の射”に“モデル空間/モデル空間の射”を対応させる関手 $`\mrm{Model}`$ を、モデル空間関手〈model-space functor〉、または単にモデル関手〈model functor〉と呼びます。ここでのモデル空間関手は、次のプロファイル(域・余域の仕様)を持ちます。
$`\quad \mrm{Model} : {\bf Eq2GRAPH}^\op \to {_1 {\bf CAT}} \In \mathbb{CAT}`$
これを次のようなファイバー付きモデル空間関手〈fibered model-space functor〉に拡張します。
$`\quad \mrm{FibModel} : {\bf RelEq2GRAPH}^\op \to {_1 {\bf FibCAT}} \In \mathbb{CAT}`$
まず、$`\mrm{FibModel}`$ の域である圏 $`{\bf RelEq2GRAPH}`$ を構成しましょう。圏 $`{\bf RelEq2GRAPH}`$ は、相対指標〈フレーム付き指標〉の圏です。対象は相対指標 $`(\Sigma_0 \subseteq \Sigma_1)`$ です。そして、2つの相対指標のあいだの射は、次の図式を可換にする射のペア $`(\varphi_0 , \varphi1)`$ です。
$`\quad \xymatrix{
\Sigma_0 \ar[r]^{\varphi_0} \ar@{_{(}->}[d]
& \Gamma_0 \ar@{_{(}->}[d]
\\
\Sigma_1 \ar[r]^{\varphi_1}
& \Gamma_1
}\\
\quad \text{commutative }\In {\bf Eq2GRAPH}
`$
射の結合〈composition〉と恒等射は明らかでしょう。上記の射は次のように書きます。
$`\quad (\varphi_0 \subseteq \varphi_1) : (\Sigma_0\subseteq \Sigma_1)
\to (\Gamma_0\subseteq \Gamma_1) \In {\bf RelEq2GRAPH}
`$
相対指標 $`\Sigma`$ から誘導される指標の包含射〈inclusion morphism〉は、ギリシャ文字イオタにより次のように書くことにします。
$`\quad \iota_\Sigma : \Sigma_0 \incto \Sigma_1 \In {\bf Eq2GRAPH}`$
モデル空間関手 $`\mrm{Model}`$ は反変関手なので、相対指標の包含射から、次のような関手が得られます。
$`\quad \mrm{Model}(\iota_\Sigma) : \mrm{Model}(\Sigma_1) \to \mrm{Model}(\Sigma_0)
\In {\bf CAT}
`$
これは、圏のファイブレーションとなります。そのことを示すのは今は棚上げにして、ファイブレーションになる場合を考えると思ってください。ファイブレーション(の射影)を特別な矢印で書くことにします。
$`\quad \mrm{Model}(\iota_\Sigma) : \mrm{Model}(\Sigma_1) \epito \mrm{Model}(\Sigma_0)
\In {\bf CAT}
`$
この形(アローヘッドが二重)の矢印は、包含射 $`\iota_\Sigma`$ で誘導されたファイブレーション(の射影)を表すと約束します。矢印に付けるラベルは省略します。
圏のファイブレーション、つまりファイバー付き圏〈fibered category〉を対象として、ファイバー付き関手(「グロタンディーク構成・逆構成と同値対応」参照)を射とする1-圏を $`{_1{\bf FibCAT}}`$ とすると、次のように書けます。
$`\quad (\mrm{Model}(\Sigma_1) \epito \mrm{Model}(\Sigma_0) )
\in |{_1 {\bf FibCAT}}|
`$
これが $`\mrm{FibModel}`$ の対象パートを与えます。つまり:
$`\quad \mrm{FibModel}(\Sigma) := (\mrm{Model}(\Sigma_1) \epito \mrm{Model}(\Sigma_0) ) \; \in |{_1 {\bf FibCAT}}|
`$
$`\varphi : \Sigma \to \Gamma`$ が相対指標のあいだの射のとき、相対指標の射を定義する図式を、関手 $`\mrm{Model}`$ で $`{_1 {\bf s2CAT}^\mrm{str}}`$ に送ると次の図式ができます。
$`\quad \xymatrix@C+1.5pc {
\mrm{Model}(\Sigma_0)
& \mrm{Model}(\Gamma_0) \ar[l]_{\mrm{Model}(\varphi0)}
\\
\mrm{Model}(\Sigma_1) \ar@{->>}[u]
& \mrm{Model}(\Gamma_1) \ar[l]_{\mrm{Model}(\varphi_1)} \ar@{->>}[u]
}\\
\quad \text{commutative }\In {_1 {\bf s2CAT}^\mrm{str}}
`$
この図式が、ファイバー付き圏〈ファイブレーション〉の射=ファイバー付き関手になるかどうかは定かではないですが、今はファイバー付き関手になる状況を考えることにします。すると、上の図式は次のように書けます。
$`\quad \mrm{FibModel}(\varphi) : \mrm{FibModel}(\Gamma) \to \mrm{FibModel}(\Sigma)
\In {\bf FibCAT}
`$
これが $`\mrm{FibModel}`$ の射パートを与えます。
細部の確認をせずに、都合のよい状況を考えるとして話を進めていますが、次の関手が定義できたとしましょう。
$`\quad \mrm{FibModel} : {\bf RelEq2GRAPH}^\op \to {_1 {\bf FibCAT}} \In \mathbb{CAT}`$
相対指標 $`\Sigma`$ に対する $`\mrm{FibModel}(\Sigma)`$ を、$`\Sigma`$ のファイバー付きモデル空間〈fibered model space〉、またはモデル・ファイバー付き圏〈model fibered category〉と呼びます。
一般化対象とフレーム条件
フレーム充填問題は、フレーム付き指標=相対指標 とフレーム条件から構成されます。相対指標は、ファイバー付きモデル空間関手によりターゲットに送られてファイバー付き圏を定義することが前節で分かりました。この節では、フレーム条件の定式化を考えます。
$`{\bf 1}`$ は、集合圏の特定された単元集合〈distinguished singleton set〉を指す名前ですが、単一対象単一射の自明圏や、各次元の自明n-圏を指すためにも流用〈オーバーロード〉します。
$`\cat{C}`$ がn-圏(n = 0, 1, 2, ...)のとき、$`{\bf 1}`$ からのn-関手〈(n, 0)-変換手〉 $`A`$ は、$`\cat{C}`$ の対象と同一視可能です。
$`\quad A:{\bf 1} \to \cat{C} \In n{\bf Cat}`$
n = 0 のときは、$`A`$ は要素/点を表し、n ≧ 1 のときは対象を表します。ときに、要素/点/対象をインスタンス/住人〈habitant〉と呼んだりもします。
自明n-圏(n-圏達の(n + 1)-圏の終対象)の代わりに、任意の対象 $`X`$ からの1-射を、$`\cat{C}`$ の一般化対象〈generalized object〉と呼びます。
$`\quad A: X \to \cat{C} \In n{\bf Cat}`$
状況により、一般化点〈generalized point〉や一般化インスタンス〈generalized instance〉などの言葉も使います。$`X`$ をパラメーター空間またはインデキシング空間とみて、パラメーター付き対象〈parameterized object〉、インデックス付きオブジェクト〈indexed object〉などと呼ぶこともあります。
次の正規表現は、たくさんの同義語を生み出しますが、意味は同じです。
{一般化 | パラメーター付き | インデックス付き}{要素 | 点 | 対象 | インスタンス | 住人}
さて、フレーム問題のフレーム条件は次の一般化対象だと定義します。
$`\quad A:\cat{X} \to \mrm{Model}(\Sigma_0) \In {\bf CAT}`$
$`X = {\bf 1}`$ と置けば、フレーム上で定義されたモデル(モデル圏の対象)がフレーム条件です。
$`\quad A:{\bf 1} \to \mrm{Model}(\Sigma_0) \In {\bf CAT}`$
フレーム充填問題の解空間関手
フレーム充填問題は、$`( \Sigma , A) = ( (\Sigma_0\subseteq \Sigma_1), A)`$ によって記述されます。ここで、$`\Sigma`$ は相対指標〈フレーム付き指標〉で、$`A`$ はモデル圏 $`\mrm{Model}(\Sigma_0)`$ の一般化対象〈一般化インスタンス〉です。
モデルのターゲットは $`{\bf Cat}`$ に決め打ちだとして、フレーム充填問題 $`( \Sigma , A)`$ の解空間を、次のように書きます。
$`\quad \mrm{Sol}(\Sigma, A)`$
今のところ、書き方を決めただけで、$`\mrm{Sol}(\Sigma, A)`$ は正体不明です。
とりあえず、$`\Sigma = (\Sigma_0 \subseteq \Sigma_1)`$ はひとつ選んで固定することにして、フレーム条件を動かしたときに解空間がどう変化するかを見ることにします。つまり、次のような対応を考えることにします。
$`\quad A \mapsto \mrm{Sol}_\Sigma(A) = \mrm{Sol}(\Sigma, A)`$
フレーム条件 $`A`$ は、前節で述べたように一般化対象なので、その全体は次の圏となります。
$`\quad {_1 {\bf CAT}}/\mrm{Model}(\Sigma_0)`$
この圏は、とても大きな2-圏 $`{\bf CAT}`$ を切り落とした〈truncated〉とても大きな1-圏 $`{_1 {\bf CAT}}`$ のスライス圏〈オーバー圏〉です。この圏の対象は、任意の圏 $`\cat{X}`$ から $`\mrm{Model}(\Sigma_0)`$ への射〈関手〉なので次の形です。
$`\quad A:\cat{X} \to \mrm{Model}(\Sigma_0) \In {_1 {\bf CAT}}`$
これは確かにフレーム条件です。
さて、相対指標〈フレーム付き指標〉が $`\Sigma`$ であり、フレーム条件が $`A`$ であるフレーム充填問題の解空間とは何でしょうか? それは、相対指標が定義するファイブレーションとフレーム条件のファイバー積です。
$`\quad \xymatrix{
{\mrm{Sol}_\Sigma(A)} \ar@{->>}[d] \ar[r]
\ar@{}[dr]|{\text{p.b.}}
&{\mrm{Model}(\Sigma_1)} \ar@{->>}[d]
\\
\cat{X} \ar[r]_-{A}
&{\mrm{Model}(\Sigma_0)}
}\\
\quad \In {_1 {\bf CAT}}
`$
ファイブレーションのファイバー引き戻しはファイブレーションなので、$`(\mrm{Sol}_\Sigma(A) \epito \cat{X})`$ はファイブレーション〈ファイバー付き圏〉になります。解空間をトータル圏とするファイブレーションを次のように書くことにします。
$`\quad \mrm{FibSol}_\Sigma(A) := (\mrm{Sol}_\Sigma(A) \epito \cat{X}) \;\in |{\bf FibCAT}|`$
解空間(1-圏) $`\mrm{Sol}_\Sigma(A)`$ は、一般化対象 $`A`$ のインデキシング空間 $`\cat{X}`$ の上にファイブレーションの構造を持つので、それをファイバー付き解空間〈fibered solution space〉と呼びましょう。$`\cat{X} = {\bf 1}`$ のときは、単一の1-圏です。
上のプルバック四角形は次のように書き換えることができます。
$`\quad \mrm{FibSol}_\Sigma(A) \to \mrm{FibModel}(\Sigma) \In {\bf FibCAT}`$
これはファイバー付き圏達の圏の射ですが、余域は $`\mrm{FibModel}(\Sigma)`$ です。したがって、スライス圏の対象とみなせます。
$`\quad (\mrm{FibSol}_\Sigma(A) \to \mrm{FibModel}(\Sigma)) \in |{\bf FibCAT}/\mrm{FibModel}(\Sigma)|`$
ここまでで、いくつかのレベルの対応を出したので、まとめておきます。
$`\quad A \mapsto \mrm{Sol}_\Sigma(A) \in |{\bf CAT}|\\
\quad A \mapsto (\mrm{Sol}_\Sigma(A) \epito \cat{X}) \;\in |{\bf FibCAT}| \\
\quad A \mapsto (\mrm{FibSol}_\Sigma(A) \to \mrm{FibModel}(\Sigma)) \in |{\bf FibCAT}/\mrm{FibModel}(\Sigma)|
`$
スライス圏の対象はバンドル〈bundle〉と呼んでいる*4ので、3番目の対応は、一般化対象であるフレーム条件にファイバー付き圏のバンドルを割り当てています。
上記の対応は、対象に対象を割り当ててますが、対応を射にまで拡張して関手にすることができます。解空間関手としてどの関手を使うかは目的・用途によります。
そしてそれから
細部の確認は省略して、都合のよい想定により大雑把な話をしました。後半はだいぶ急ぎ足だったし色々と中途半端ですが、この記事の内容を他の概念やフレームワークと組み合わせて応用しようと思っています。フレーム充填問題と解空間の概念は、関手のラムダ計算とでもいうべき計算体系に組み入れられそう、たぶん。
指標とモデルに関しては、構文付き変換手インスティチューション(「構文付き変換手インスティチューション 1/n」参照)のフレームワークが使えるでしょう。ファイブレーションの扱いは、ファイブレーション達を射のクラス(「射のクラスと制約付きスパン」)と考えたほうが良さそうです。‥‥ 続きはまた。