回転群の指数写像の具体的な表示と計算 - 檜山正幸のキマイラ飼育記 (はてなBlog)

「回転群の具体的な表示と計算」に少し追加します。Mさんが知りたかったのは指数写像らしいので、指数写像について述べます。「回転群の具体的な表示と計算」と同様、群論、多様体論、微分幾何学などは出来るだけ使わずに、行列計算とRⁿの幾何的直感を頼りに話をします。

内容：

指数関数・三角関数の級数表示
行列の指数関数
2次歪対称行列の指数関数
指数写像の解釈
SO(n)の単位元における接空間
指数法則
指数写像の微分
1パラメータ指数写像
Alt(3)の基底と回転の力学

指数関数・三角関数の級数表示

指数関数は次の級数表示を持ちます。

e^x = exp(x) = 1 + x + (1/2!)x² + (1/3!)x³ + ... + (1/n!)xⁿ + ...

右辺の無限級数を適当なところで打ち切った多項式で、指数関数は近似されます。実験として、4次の多項式 1 + x + (1/2)x² + (1/6)x³ + (1/24)x⁴ と指数関数を比較してみます*1。

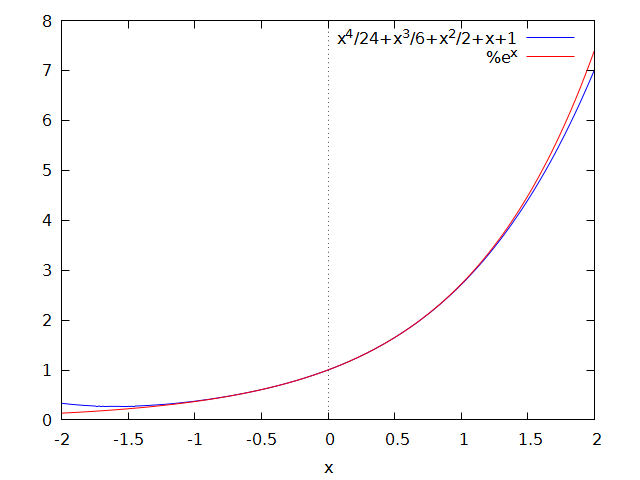
x = 0 の周辺なら、まーまーの近似になっています。

三角関数も級数で表示できます。

cos(x) = 1 - (1/2!)x² + (1/4!)x⁴ - ... + (-1)ⁿ(1/(2n)!)x²ⁿ + ...
sin(x) = x - (1/3!)x³ + (1/5!)x⁵ - ... + (-1)ⁿ(1/(2n+1)!)x²ⁿ⁺¹ + ...

複素数を使うと指数関数と三角関数を関係付けられます（オイラーの公式）が、今回は実数の範囲で考えます*2。

行列の指数関数

M2は、前回記事「回転群の具体的な表示と計算」で定義したように、2次行列環です。その他の記号・記法も前回記事と同様です。X∈M2に対して、指数関数Exp(X)を次のように定義します。

Exp(X) := E + X + (1/2!)X² + (1/3!)X³ + ... + (1/n!)Xⁿ + ...

上の定義が意味を持つには次のことを調べる必要があります。

無限級数を打ち切った多項式関数が意味を持つか？
無限級数を近似する多項式関数の列は収束するか？
収束先である関数は良い性質を持つか？

今はこれらのことを詮索しません。Exp(X)はちゃんと定義されていると思ってください。試しに、2次行列Xに対する3次の近似多項式を求めてみます。あっ、「2次」は行列のサイズで「3次」は多項式の次数ね、紛らわしいけど。以下に、Maximaのコードと画面ショットです。

Exp3(X) := E + X + 1/2*X^^2 + 1/6*X^^3
X;
Exp3(X);
A : matrix([0, -1/4], [1/4, 0])
Exp3(A)

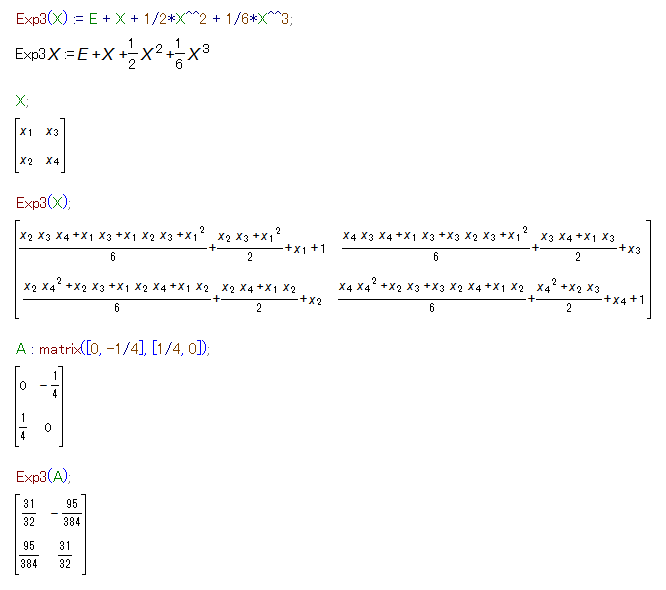
行列の指数関数 Exp:M2→M2 を上記のように定義できますが、M2は非可換で実数体より複雑な構造を持つので、一般的には指数法則 Exp(X + Y) = Exp(X)・Exp(Y) は成立しません。特別なX, Yの組み合わせや、定義域を制限すると指数法則が成立することもあります。

すぐ上で使ったナカグロ記号'・'は行列の掛け算の意味です。前回記事「回転群の具体的な表示と計算」ではリング記号' $\circ$ 'を使いましたが、今回は写像の結合（合成）が出てくるので、' $\circ$ 'は写像の結合の意味で使います。

2次歪対称行列の指数関数

X^t = -X を満たすような2次行列を2次の歪対称行列（skey-symmetric matrix）と呼びます。歪対称行列は、反対称行列（antisymmetric matrix）、交代行列（alternative matrix）とも呼ばれます。

X^t = -X を成分で表示すると：

$\begin{pmatrix}{\it x_1} & {\it x_2} \\ {\it x_3} & {\it x_4} \\ \end{pmatrix}=\begin{pmatrix}-{\it x_1} & - {\it x_3} \\ -{\it x_2} & -{\it x_4} \\ \end{pmatrix}$

成分ごとに見ると：

x₁ = -x₁
x₃ = -x₂
x₂ = -x₃
x₄ = -x₄

これより、

x₁ = x₄ = 0
x₃ = -x₂

が出ます。結局、2次の歪対称行列は s = x₂ と置いて次の形になります。

$S = \begin{pmatrix} 0 & -s \\ s & 0 \end{pmatrix}$

歪対称行列Sに関してその指数関数値 Exp(S) を具体的に計算してみましょう。

$\mathrm{Exp}(S) = \mathrm{Exp}\left( \begin{pmatrix} 0 & -s \\ s & 0\end{pmatrix} \right) = \mathrm{Exp}\begin{pmatrix} 0 & -s \\ s & 0\end{pmatrix}$

試しに、Sの累乗を求めてみます。

$S^0 = \begin{pmatrix}1 & 0 \\ 0 & 1 \\ \end{pmatrix}$
$S^1 = \begin{pmatrix}0 & -s \\ s & 0 \\ \end{pmatrix}$
$S^2 = \begin{pmatrix}-s^2 & 0 \\ 0 & -s^2 \\ \end{pmatrix}$
$S^3 = \begin{pmatrix}0 & s^3 \\ -s^3 & 0 \\ \end{pmatrix}$
$S^4 = \begin{pmatrix}s^4 & 0 \\ 0 & s^4 \\ \end{pmatrix}$

偶数ベキのときは対角行列、奇数ベキのときは歪対称行列になります。次の形ですね。

$S^{2n} = \begin{pmatrix}(-1)^n s^{2n} & 0 \\ 0 & (-1)^n s^{2n} \\ \end{pmatrix}$
$S^{2n+1} = \begin{pmatrix}0 & (-1)(-1)^n s^{2n+1} \\ (-1)^n s^{2n+1} & 0 \\ \end{pmatrix}$

この形は、nに関する数学的帰納法で確認できます。

指数関数の無限級数表示を、偶数ベキと奇数ベキのペアを使って書くと次のように計算できます。

$\sum_{n=0}^{\infty}(\frac{1}{2n!}S^{2n} + \frac{1}{(2n+1)!}S^{2n+1})$
$=\, \sum_{n=0}^{\infty}\left( \frac{1}{2n!}\begin{pmatrix}(-1)^n s^{2n} & 0 \\ 0 & (-1)^n s^{2n} \\ \end{pmatrix} + \frac{1}{(2n+1)!}\begin{pmatrix}0 & (-1)(-1)^n s^{2n+1} \\ (-1)^n s^{2n+1} & 0 \\ \end{pmatrix} \right)$
$=\, \sum_{n=0}^{\infty} \begin{pmatrix}(-1)^n \frac{1}{2n!}s^{2n} & (-1)(-1)^n \frac{1}{(2n +1)!}s^{2n+1} \\ (-1)^n \frac{1}{(2n +1)!}s^{2n+1} & (-1)^n \frac{1}{2n!}s^{2n} \\ \end{pmatrix}$
$=\, \begin{pmatrix}\sum_{n=0}^{\infty}(-1)^n \frac{1}{2n!}s^{2n} & (-1)\sum_{n=0}^{\infty}(-1)^n \frac{1}{(2n+1)!}s^{2n+1} \\ \sum_{n=0}^{\infty}(-1)^n \frac{1}{(2n+1)!}s^{2n+1} & \sum_{n=0}^{\infty}(-1)^n \frac{1}{2n!}s^{2n} \\ \end{pmatrix}$
$=\, \begin{pmatrix}cos(s) & -sin(s) \\ sin(s) & cos(s) \end{pmatrix}$

等式変形の最後のステップでは、冒頭で挙げた三角関数の級数表示を使っています。まとめると：

$\mathrm{Exp}(S) = \mathrm{Exp}\begin{pmatrix}0 & -s \\ s & 0 \\ \end{pmatrix} = \begin{pmatrix}cos(s) & -sin(s) \\ sin(s) & cos(s) \end{pmatrix}$

指数写像の解釈

前節の計算から、行列の指数関数（指数写像とも呼びます）を2次歪対称行列に制限すると、SO2のパラメータ表示（前回記事参照）になることが分かりました。このことをもう少しハッキリ述べましょう。

前節の歪対称行列Sは、スカラーパラメータsに依存するので、正確に書けばS(s)です。つまり、Sは実数RからM2への写像 S:R→M2 （M2 $\stackrel{\sim}{=}$ R⁴）です。

$S(s) = \begin{pmatrix}0 & -s \\ s & 0\end{pmatrix} = \begin{pmatrix}0 & -1 \\ 1 & 0\end{pmatrix}s$

一方、SO2のパラメータ表示 R:R→M2 （M2 $\stackrel{\sim}{=}$ R⁴）は次の形です。

$R(s) = \begin{pmatrix} cos(s) & -sin(s) \\ sin(s) & cos(s)\end{pmatrix}$

SとR、指数写像 Exp:M2→M2 の関係は：

Exp $\circ$ S = R :R→M2

今出てきた $\circ$ は写像の反図式順結合で行列の掛け算ではありません。

以上の事実から、2次歪対称行列の指数（Expによる値）は2次特殊直交群SO2のなかに入ることがわかります。このことは、2次行列に限らず、任意のnに関して言えます。つまり、n次歪対称行列の指数はn次特殊直交群SO(n)のなかに入ります。その理由を次節以降で述べます。

SO(n)の単位元における接空間

歪対称行列が唐突に出てきた印象があるでしょうが、SO(n)の単位元E_nでの接空間が歪対称行列の空間になります。このことを見るには、F:R⊇(-ε, ε)→SO(n) という写像を考えます。εは正の実数または∞で、(-ε, ε)は原点の回りの適当な開区間を意味します。特に、(-∞, ∞) = R です。

Fは、開区間(-ε, ε)からR^n×nへの写像で、SO(n)からはみ出さないものと考えることができます。(n×n)次元のベクトル値の1変数関数なので、微分可能性や微分（導関数）も定義できます。

F:(-ε, ε)→SO(n) が（何度でも）微分可能な関数として、F(0) = E_n と仮定します。Fの微分（導関数）はF'と書きます。Fが(n×n)次元のベクトル値1変数関数なので、F'も同じく(n×n)次元のベクトル値1変数関数です。行列の転置や掛け算に関して、次の微分公式が成立します。次の公式で・は行列の掛け算です。

(F^t)' = (F')^t
(G・F)' = G'・F + G・F'
(定数関数)' = O_n （O_nはR^n×nのゼロベクトル）

これらの微分公式を使って、F(s)^t・F(s) = E_n （F(s)∈SO(n) を表す等式）の両辺を微分すると：

F'(s)^t・F(s) + F(s)^t・F'(s) = O_n

s = 0 での値を考えると：

F'(0)^t・F(0) + F(0)^t・F'(0) = O_n

F(0) = F(0)^t = E_n （単位行列）と仮定していたので：

F'(0)^t + F'(0) = O_n
つまり、F'(0)^t = -F'(0)

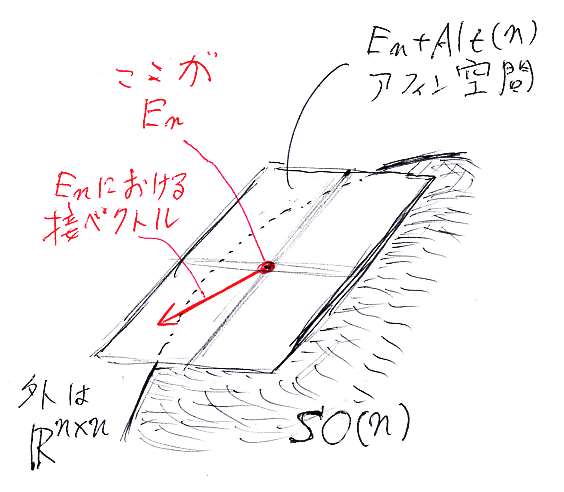
これは、Fの0での微分係数F'(0)が歪対称行列であることを示します。実パラメータsを時間と考えれば、FはSO(n)の上を動く運動の表示です。そして、F'(0)は、F(0) = E_nでの速度ベクトルなので、「図形SO(n)の一点E_nにおける接ベクトル」と解釈できます。つまり、SO(n)のE_nにおける接ベクトルは歪対称行列であり、接空間（接ベクトルの全体）は歪対称行列の空間になります。

n次歪対称行列は、対角線より上の成分だけで決定されるので、(n×n - n)/2 = n(n - 1)/2 個の独立な成分を持つことになり、ベクトル空間としての次元はn(n - 1)/2です。このことから、SO(n)の図形としての次元もn(n - 1)/2だろうと推測できます。

n次歪対称行列の全体をAlt(n)としましょう。'Alt'は歪対称行列の同義語「交代行列」（alternative matrix）からです。今までの議論から、Alt(n)⊆R^n×n は部分ベクトル空間で、dim(Alt(n)) = n(n - 1)/2、E_n + Alt(n) = {E_n + X | X∈Alt(n)} はSO(n)の接空間となります。

指数法則

行列の指数関数でも、特別な条件を付ければ指数法則が成立します。AとBが可換（A・B = B・A）なとき、次が成立します。

Exp(A + B) = Exp(A)・Exp(B)

これを示すには形式的ベキ級数のレベルでの形式的計算と、収束に関する議論が必要です。僕は、形式的計算もなんだかよく分からなかった記憶があるので、少し丁寧に説明します。

背景になるのは、Vをノルム付きベクトル空間（V = R と考えてもよい）として、Ψ:N×N→V の総和を求める公式です。Ψが総和可能なとき、N×Nをどのように分割して総和を計算してもよいので、N×N = {(0, 0)}∪{(1, 0), (0, 1)}∪{(2, 0), (1, 1), (0, 2)}∪... のような分割で計算します。

$\sum_{(k, l) \in \bf{N}\times\bf{N}} \psi(k, l) \,= \sum_{n \in \bf{N}} \left(\sum_{(k, l) \in \{(\mu, \nu) \in \bf{N}\times\bf{N} | \mu + \nu = n\}} \psi(k, l) \right)$

書き方を変えると：

$\sum_{(k, l) \in \bf{N}\times\bf{N}} \psi(k, l) \, = \sum_{n = 0}^{\infty}\left(\sum_{k + l = n} \psi(k, l)\right)$

縦割り／横割りによる総和も考えれば：

$\sum_{(k, l) \in \bf{N}\times\bf{N}} \psi(k, l) \, =\sum_{k=0}^{\infty}\sum_{l=0}^{\infty}\psi(k, l) \, = \sum_{l=0}^{\infty}\sum_{k=0}^{\infty}\psi(k, l) \, = \sum_{n = 0}^{\infty}\left(\sum_{k + l = n} \psi(k, l)\right)$

このように、分割方法を変えても総和は変わらないことを利用して、Exp(A + B) = Exp(A)・Exp(B) を示します。

まず Exp(A + B)を計算します。

$\mathrm{Exp}(A + B) \, = \sum_{n = 0}^{\infty} \frac{1}{n!}(A + B)^n$

(A + B)ⁿ を二項展開します。

$\mathrm{Exp}(A + B) \, = \sum_{n = 0}^{\infty} \frac{1}{n!}\left(\sum_{k=0}^{n} \frac{n!}{k!(n-k)!} A^k B^{n - k} \right)$

n!を約分してn - kをℓと置けば：

$\mathrm{Exp}(A + B) \, = \sum_{n = 0}^{\infty} \left(\sum_{k + l = n} \frac{1}{k!l!} A^k B^l \right)$

次に、Exp(A)・Exp(B)を計算します。

$\mathrm{Exp}(A)\cdot\mathrm{Exp}(B) \, = \left(\sum_{k=0}^{\infty} \frac{1}{k!}A^k \right)\cdot \left(\sum_{l=0}^{\infty} \frac{1}{l!}B^l \right) \, = \sum_{k=0}^{\infty}\sum_{l=0}^{\infty} \frac{1}{k!l!} A^k\cdot B^l$

分割方法を変えても総和は変わらないことから：

$\sum_{n = 0}^{\infty} \left(\sum_{k + l = n} \frac{1}{k!l!} A^k B^l \right) \, = \sum_{k=0}^{\infty}\sum_{l=0}^{\infty} \frac{1}{k!l!} A^k\cdot B^l$

これで、形式的計算においては Exp(A + B) = Exp(A)・Exp(B) を示せました。このような計算が行えたのは、A・B = B・A が仮定されていたからです。任意のA, Bに対して指数法則は成立しません。形式的計算が実際の値の計算になっていることは、解析学の総和・収束の議論を適用して分かりますが、そこは割愛します。

Aをn次正方行列、s, tを実数とするとき、AsとAtは可換なので、次が成立します。

Exp(A(s + t)) = Exp(As + At) = Exp(As)・Exp(At)

また、Aと-Aも可換なので（E_nはn次単位行列、O_nはn次ゼロ行列として）、

E_n = Exp(O_n) = Exp(A + (-A)) = Exp(A)・Exp(-A)

これより、

Exp(-A) = Exp(A)^-1

が出ます。

指数写像の微分

n次行列環Mnにおける指数写像 Exp:Mn→Mn は、ユークリッド空間のあいだの写像とみなせば、Exp:R^n×n→R^n×n です。その微分を表すヤコビ行列は、(n×n)×(n×n)行列になります。例えば、3次行列環の指数写像の微分（ヤコビ行列）は、81成分を持つ行列になります。

しかし、環の加減乗除（除は逆数を取ること）で組み立てられる多項式関数やその極限である無限級数（で定義される関数）では、微分も加減乗除の組み合わせで書けるので、実数値1実変数関数の微分計算と類似の微分公式が成立します。

例えば、 $\frac{d}{dx} e^x = e^x$ と類似の次の微分公式が成立します。

$\frac{d}{dX} \mathrm{Exp}(X) = \mathrm{Exp}(X)$

とはいえ、この微分公式の解釈はけっこう難しいです。

F:R^N→R^M をユークリッド空間のあいだの微分可能写像として、その導関数（各点のヤコビ行列を対応させる写像）をD[F]とします。Dは微分作用素です。D[F]の特定の点Aでの値（微分係数＝ヤコビ行列）を D[F](A) と書くことにします。D[F](A)はM行N列の行列です。この行列と長さNの列ベクトルY（Y∈R^N）との積は併置により D[F](A) Y と書くことにします。

今説明した記法で書くと、指数写像の微分公式は次のことを意味します。

D[Exp](A) Y = Exp(A)・Y

もう少し馴染みのある書き方をするなら：

$[\frac{d}{dX} \mathrm{Exp}(X)]_{X=A}Y = \mathrm{Exp}(A)\cdot Y$

左辺の $[\frac{d}{dX} \mathrm{Exp}(X)]_{X=A}$ は(n×n)×(n×n)行列で、Yはn×n行列を長さn×nの列ベクトルとみなしたものです。右辺は、(n×n)行列の掛け算（記号'・'）です。

n = 2 のケースを、X, A, Yなどをタプル（列ベクトル）形式で書いてみると次のようになります。Exp(X)の第i成分はe_i（i = 1, 2, 3, 4）と略記し、B = Exp(A) と置きました。

$\begin{pmatrix}\frac{\partial \mathrm{e}_1}{\partial x_1} & \frac{\partial \mathrm{e}_1}{\partial x_2} & \frac{\partial \mathrm{e}_1}{\partial x_3} & \frac{\partial \mathrm{e}_1}{\partial x_4} \\ \frac{\partial \mathrm{e}_2}{\partial x_1} & \frac{\partial \mathrm{e}_2}{\partial x_2} & \frac{\partial \mathrm{e}_2}{\partial x_3} & \frac{\partial \mathrm{e}_2}{\partial x_4} \\ \frac{\partial \mathrm{e}_3}{\partial x_1} & \frac{\partial \mathrm{e}_3}{\partial x_2} & \frac{\partial \mathrm{e}_3}{\partial x_3} & \frac{\partial \mathrm{e}_3}{\partial x_4} \\ \frac{\partial \mathrm{e}_4}{\partial x_1} & \frac{\partial \mathrm{e}_4}{\partial x_2} & \frac{\partial \mathrm{e}_4}{\partial x_3} & \frac{\partial \mathrm{e}_4}{\partial x_4} & \\ \end{pmatrix}_{\begin{pmatrix}x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix}=\begin{pmatrix}a_1 \\ a_2 \\ a_3 \\ a_4\end{pmatrix}} \begin{pmatrix}y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix}$
$= \mathrm{Exp}(\begin{pmatrix}a_1 \\ a_2 \\ a_3 \\ a_4\end{pmatrix})\cdot \begin{pmatrix}y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix}$
$= \begin{pmatrix}b_1 \\ b_2 \\ b_3 \\ b_4\end{pmatrix} \cdot \begin{pmatrix}y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix}$
$= \begin{pmatrix}{\it b_3}\,{\it y_2}+{\it b_1}\,{\it y_1} \\ {\it b_4}\, {\it y_2}+{\it b_2}\,{\it y_1} \\ {\it b_3}\,{\it y_4}+{\it b_1}\,{\it y_3} \\ {\it b_4}\,{\it y_4}+ {\it b_2}\,{\it y_3} \\ \end{pmatrix}$
$= \begin{pmatrix} b_1 & b_3 & 0 & 0 \\ b_2 & b_4 & 0 & 0 \\ 0 & 0 & b_1 & b_3 \\ 0 & 0 & b_2 & b_4 \\ \end{pmatrix} \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix}$

このへんのことをチャンと書いてある資料をあまり見かけないので、一度チャンと書きたいなとは思っているのですが、今日のところはコレでお茶を濁して、合成関数の微分公式に話を進めます。

IをRの開区間として、微分可能な写像 G:I→R^n×n を考えます。このR^n×nはMnとみなせば、GとExp:R^n×n→R^n×n は結合（合成）可能です。Exp $\circ$ G:I→R^n×n の微分（導関数）は次の公式で与えられます。

$\frac{d}{ds}(\mathrm{Exp}\circ G)(s) = [\frac{d}{dX}\mathrm{Exp}]_{X=G(s)}\, \frac{d}{ds}G(s)$

先の、指数写像の微分公式と組み合わせると：

$\frac{d}{ds}(\mathrm{Exp}\circ G)(s) = \mathrm{Exp}(G(s))\cdot \frac{d}{ds}G(s)$

これらの微分公式は次節で使います。

1パラメータ指数写像

「SO(n)の単位元における接空間」の節において、次のことを示しました；（何度でも）微分可能な F:(-ε, ε)→SO(n), F(0) = E_n に対して、その微分F'(0)はAlt(n)に入る。さてそれでは、A∈Alt(n) を先に与えて、Aを微分係数（速度ベクトル）とするような標準的な関数 H:(-ε, ε)→SO(n) を定義できるでしょうか？標準的とは、Aを決めると関数Hも一意的に決まることです。

前段落の問題をチャンと述べると； H:(-ε, ε)→Mn （Mn $\stackrel{\sim}{=}$ R^n×n）を未知関数とする以下の常微分方程式を解くことになります。ここで、Mnはn次行列の空間です。

H(0) = E_n
H'(s) = H(s)・A （A∈Alt(n)）

常微分方程式の解の存在と一意性から、上記の条件を満たすHが決まることは分かりますが、ここでは、天下りかつ具体的・露骨に解を与えてしまいます。

H(s) := Exp(As)

Hの定義域である開区間(-ε, ε)は適当に考えていいですが、(-∞, ∞) = R でも定義可能です。

実変数sの関数Exp(As)が、実際に常微分方程式を満たすことを確認します。H(0)は次のように計算できます

  H(0)
= Exp(A0)
= Exp(O_n)
= E_n

次に微分（導関数）H'(s)を計算します。分かりやすいように、G(s) := As と置いて、H(s) = (Exp $\circ$ G)(s) とします。G'(s) = A（定数関数）に注意して、指数写像の微分公式と合成関数の微分公式により、

  H'(s)
= Exp(G(s))・G'(s)
= Exp(As)・A
= H(s)・A

特に、

  H'(0)
= Exp(A0)・A
= Exp(O_n)・A
= E_n・A
= A

以上で、A∈Alt(n) に対して、標準的な関数 s|→Exp(As) を対応させることができました。この関数は1つの実数パラメータだけを持つ指数写像です。

A∈Alt(n) に対するExp(As)は、実数sの値が何であっても Exp(As)∈SO(n) となります。このことは次の計算で分かります。

  Exp(As)^t
= Exp(A^ts)
// Aが歪対称行列なので、A^t = -A
= Exp(-As)
// 「指数法則」の節で示した等式により
= Exp(As)^-1

X = Exp(As) と置けば、上の計算は X^t = X^-1 を意味するので、X^t・X = E_n すなわち X = Exp(As) ∈SO(n) 。

「指数法則」の節で示した等式により、

Exp(A(s + t)) = Exp(As)・Exp(At)
Exp(A0) = E_n
Exp(A(-s)) = Exp(As)^-1

これは、1パラメータ指数写像Exp(As)が、加法群RからSO(n)への群の準同型写像であることを意味しています。

Alt(3)の基底と回転の力学

n = 3 のケースを考えます。Alt(3)は R^3×3 = R⁹ の部分ベクトル空間になります。その次元は、3(3 - 1)/2 = 3 です。3つの歪対称行列をうまく選べば、3次元ベクトル空間Alt(3)の基底となります。例えば、次の3つの歪対称行列はAlt(3)の基底です。

$\begin{pmatrix}0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix}$
$\begin{pmatrix}0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{pmatrix}$
$\begin{pmatrix}0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$

これらが基底となるのはただちに分かりますが、いきなり出されても必然性を感じません。これら3つの歪対称行列は力学由来であることを説明します。

我々が棲んでいる空間のモデルである3次元ユークリッド空間R³の座標軸を、常識のとおりx-軸、y-軸、z-軸と呼ぶことにします。x-軸の回りの角度sの回転は、次の行列で表現できます。

$\mathrm{RX}(s) \, = \begin{pmatrix}1 & 0 & 0 \\ 0 & cos(s) & -\sin(s) \\ 0 & \sin(s) & \cos(s) \\ \end{pmatrix}$

角速度が一定なら、角度と時間は比例するので、sの代わりに時間パラメータtとしても同じことです。

$\mathrm{RX}(t) \, = \begin{pmatrix}1 & 0 & 0 \\ 0 & cos(t) & -\sin(t) \\ 0 & \sin(t) & \cos(t) \\ \end{pmatrix}$

実パラメータが角度か時間かは気にしないことにします。x-軸のときと同様に、y-軸を回りの回転とz-軸の回りの回転は次のパラメータ付き行列で表現されます。

$\mathrm{RY}(s) \, = \begin{pmatrix}\cos(s) & 0 & \sin(s) \\ 0 & 1 & 0 \\ -\sin(s) & 0 & \cos(s) \\ \end{pmatrix}$

$\mathrm{RZ}(s) \, = \begin{pmatrix}\cos(s) & -\sin(s) & 0 \\ \sin(s) & \cos(s) & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$

これらのパラメータ付き行列は、R→R^3×3 の写像です。それだけでなく、sの値によらず行列はSO(3)に入ります。さらに、加法群Rから回転群SO(3)への群の準同型になっています。つまり、RX, RY, RZは前節で説明した1パラメータの指数写像の実例です。

これらのことは、行列計算と三角関数の加法定理で示せますが、軸を固定した回転運動を考えれば直感的にも納得いくでしょう。例えば、回転の角度の和は、回転行列の積に対応します（指数法則）。

RX, RY, RZをパラメータsで微分したものを SX, SY, SZ と置くことにします。

$\mathrm{SX}(s) \,:= \frac{d}{ds}\mathrm{RX}(s) \,= \begin{pmatrix}0 & 0 & 0 \\ 0 & -\sin(s)& -\cos(s)\\ 0 & \cos(s)& -\sin(s)\\ \end{pmatrix}$
$\mathrm{SY}(s) \,:= \frac{d}{ds}\mathrm{RY}(s) \,= \begin{pmatrix}-\sin(s)& 0 & \cos(s)\\ 0 & 0 & 0 \\ -\cos(s)& 0 & -\sin(s)\\ \end{pmatrix}$
$\mathrm{SZ}(s) \,:= \frac{d}{ds}\mathrm{RZ}(s) \,= \begin{pmatrix}-\sin(s)& -\cos(s)& 0 \\ \cos(s)& -\sin(s)& 0 \\ 0 & 0 & 0 \\ \end{pmatrix}$

RX(s)は、Rⁿの運動ではなくて、SO(3)内の運動を記述します。適当に3次元定数ベクトル（初期位置ベクトル）cを取って、x(s) := RX(s) c とすれば、x(s)が3次元空間内の回転運動になります。SX(s)はRX(s)の微分なので、3次元空間の値を取らず、SX:R→R^3×3 です。RYとSY、RZとSZについても同じことです。

RX, RY, RZ はSO(3)内の運動なので、s = 0 での微分は、SO(3)の単位元における接空間であるAlt(3)に入るはずです。実際に見てみましょう。

$\mathrm{SX}(0) \, = \frac{d}{ds}\mathrm{RX}(0) \,= \begin{pmatrix}0 & 0 & 0 \\ 0 & -\sin(s)& -\cos(s)\\ 0 & \cos(s)& -\sin(s)\\ \end{pmatrix}_{s = 0} = \begin{pmatrix}0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix}$
$\mathrm{SY}(0) \, = \frac{d}{ds}\mathrm{RY}(0) \,= \begin{pmatrix}-\sin(s)& 0 & \cos(s)\\ 0 & 0 & 0 \\ -\cos(s)& 0 & -\sin(s)\\ \end{pmatrix}_{s = 0} = \begin{pmatrix}0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{pmatrix}$
$\mathrm{SZ}(0) \,:= \frac{d}{ds}\mathrm{RZ}(0) \,= \begin{pmatrix}-\sin(s)& -\cos(s)& 0 \\ \cos(s)& -\sin(s)& 0 \\ 0 & 0 & 0 \\ \end{pmatrix}_{s = 0} = \begin{pmatrix}0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$

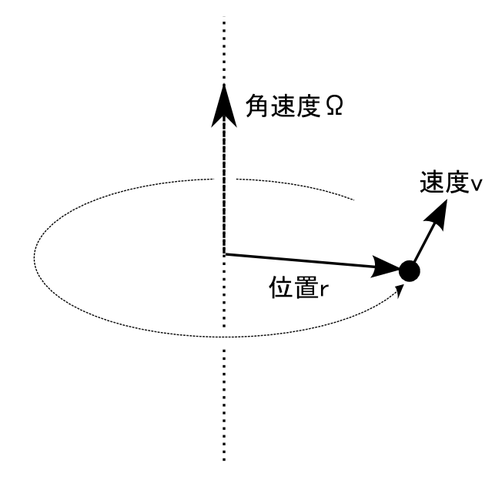
本節の冒頭に挙げた基底（3つの歪対称行列）は、RX, RY, RZの、SO(3)の単位元における速度ベクトルだったのです。これらの速度ベクトル（歪対称行列）は、“一瞬における回転させる勢い”あるいは“微小な回転”を表すものです。例えば、δを微小な角度（または時間）として、x-軸の回りの“微小な回転”は次の形です。

$\begin{pmatrix}0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix}\delta = \begin{pmatrix}0 & 0 & 0 \\ 0 & 0 & -\delta \\ 0 & \delta & 0 \end{pmatrix}$

力学で出てくる角速度や角運動量は、“一瞬における回転させる勢い”や“微小な回転”を表す量で、回転の軸方向のベクトルとして表示されます。しかし、あれは方便です。角速度や角運動量がRⁿのベクトルとして実在しているわけではありません。角速度や角運動量の本来の棲家はSO(3)の接空間です。

Alt(3)の次元が3で、上記のような標準基底を取れることから、次の1：1対応を構成できます。

$\begin{pmatrix}1 \\ 0 \\ 0\end{pmatrix} \longleftrightarrow \begin{pmatrix}0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix}$
$\begin{pmatrix}0 \\ 1 \\ 0\end{pmatrix} \longleftrightarrow \begin{pmatrix}0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{pmatrix}$
$\begin{pmatrix}0 \\ 0 \\ 1\end{pmatrix} \longleftrightarrow \begin{pmatrix}0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$

この対応を使って、Alt(3)をR³に重ね合わせているのです。この重ね合わせ（同一視）は、3次元以外では通用しません。

実際、角速度／角運動量を表す矢印は擬ベクトル（pseudovector）と呼ばれています。R³のベクトルとして考えるのはちょっと無理があるため「疑」が付いています。

イイカゲンで大雑把な話でしたが、R^2×2, R^3×3のなかにあるSO(2), SO(3)とその接空間の様子が多少はイメージできたでしょうか。

*1:実験で使う指数関数も、実際には4次多項式よりは精度のよい近似に過ぎませんが、そこはつっこまないで。実験はMaximaを使って、exp4(x) := 1 + x + 1/2*x^2 + 1/6*x^3 + 1/24*x^4; plot2d([exp4(x), exp(x)], [x, -2, 2]);

*2:オイラーの公式相当の関係式は、行列計算により再現できます。

*3:画像： https://ja.wikipedia.org/wiki/%E8%A7%92%E9%80%9F%E5%BA%A6#/media/File:Angular_velocity_jp.png