典型的な2次元の圏：双圏 その1

「ラベル付き遷移系のIO結合」において、次のように書きました。

IOインターフェースを持ったラベル付き遷移系の全体が圏になるかと言うと、色々と難しい点があります。

...(難しい点の説明)...

この状況は、豊饒圏と高次圏を組み合わせれば、うまく表現できそうです。

状態遷移の計算モデルを系統的に扱うには、どうも高次元の圏が必要そうです。一般的な高次元の圏（n-圏）は難しいので、モデリングに必要な性質を持っていて、あまり複雑ではない高次圏の定義を試みてみます。ここで紹介する「あまり複雑ではない高次圏」とは、双圏と呼ばれるものです。一度に書ききれなかったので「その1」とします。

一般的な高次圏（n-圏）の雰囲気を知るには、次の記事が多少は役に立つかも知れません。

• n-圏とは何だろう
• おとぎ話としてのn-圏 -- 計算できる図形達の世界

内容：

1. そこそこ扱いやすい高次圏とは
2. 記号と用語の約束
3. セルの集合と縦結合演算
4. 横結合演算はこの次

そこそこ扱いやすい高次圏とは

高次圏を扱うのはなかなかに難しいのですが、その理由は次のようなものでしょう。

1. 定義の仕方がいろいろある。それらの定義の相互関係が明らかではない。
2. 記述も計算も複雑になる。次元が高くなると手に負えない。

通常の圏は1-圏なので、高次圏でいちばん次元が低いものは2次元の圏です。2次元なら、まーなんとかなりそうです。以下では2次元の圏に話を限ります。

2次元の圏でも定義は何種類もあります。そのひとつに「圏の圏で豊饒化された豊饒圏」というものがあります。基本的にこの定義、つまり豊饒圏スタイルを採用します。しかし、結合律や単位律が厳密に（on-the-noseに）成立することを要求するのはキツすぎるので、up-to-isoでよいとします。こうして得られる圏が双圏（bicategory）です。

我々がこれから定義する2次元の圏である双圏は、圏の圏Catを実例として含みます。また、任意のモノイド圏の次元をずらした圏も双圏の実例となります。圏の圏とモノイド圏を実例として含むなら、ある程度の守備範囲を持つと言っていいでしょう。

記号と用語の約束

以下では、大きな集合（プロパーな類）も含めて単に「集合」と言ってしまうことにします。集合のサイズの問題は詮索しない方向で。

Cが圏のとき、対象の集合を Obj(C)、射の集合を Mor(C) と書きます。A, B∈Obj(C) に対して、ホムセットは Hom_C(A, B) ですが、下付きが面倒なので、ここでは Hom[C](A, B) と書くことにします。これらは、しばしば次のように略記されます。

1. Obj(C) は、|C| と略記。
2. Mor(C) は、単にCと略記（記号の乱用）。
3. Hom[C](A, B) は、C(A, B) と略記。

上記の略記法はとても便利ですが、高次圏を扱うときは混乱の原因ともなります。今回は略記の使用は控えめにします。

2次元の圏とは、通常の圏に対して、2次元の射が加わったものです。対象、射、2次元の射を、それぞれ、0-セル、1-セル、2-セルとも呼びます。「セル」とは、図形的な要素です。0-セルは点、1-セルは矢印、2-セルは方向が付いた膜のようなものだとイメージしてください。

次の図では、n = -1 とか n = 3 も描いてありますが、n-セル（特に n = 0, 1, 2）は、だいたいこんな感じのものです。あくまでイメージですけど。

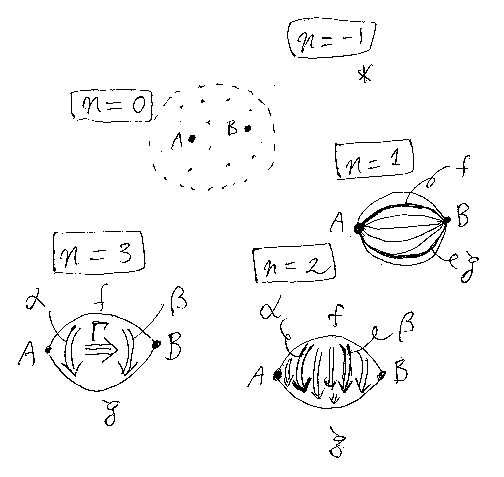
セルの集合と縦結合演算

これから、双圏Bについて記述していきます。B₀、B(-, -)、B₁(-, -)、B₂(-, -:-, -) のような記号が出てきますので注意深く区別してください。

まず、B₀は0-セルの集合とします。単なる集合で特に構造は持ちません。2つの0-セルA, B（A = B でもよい）に対して、圏 B(A, B) が対応しているとします。B(A, B) は、双圏Bのホム圏（hom category）です。B(A, B) は圏なので、Obj(B(A, B)) を考えることができます。B₁(A, B) := Obj(B(A, B)) と置いて、B₁(A, B) を、A, Bを両端とした1-セルの集合と呼びます。

f, g∈B₁(A, B) に対して、圏B(A, B)のホムセット Hom[B(A, B)](f, g) を考えることができます。B₂(f, g:A, B) := Hom[B(A, B)](f, g) と置いて、B₂(f, g:A, B) を、f, gを両端とした2-セルの集合と呼びます。

まとめると：

1. B₀ は0-セルの集合。0-セルは、A, Bなどと書く。
2. B₁(A, B) は1-セルの集合。1-セルは、f, gなどと書く。
3. B₂(f, g:A, B) は2-セルの集合。2-セルは、α, βなどと書く。

f∈B₁(A, B) であることを、f:A→B とも書きます。α∈B₂(f, g:A, B) であることを、α::f⇒g:A→B とも書きます。A, Bまで明示する必要がないときは、α∈B₂(f, g)、α::f⇒g と略記します。

B(A, B) は圏なので、射の結合（合成）と恒等射（単位）があります。圏B(A, B)の対象は1-セル、射は2-セルです。よって、α::f⇒g と β::g⇒h が結合可能で、fごとに恒等射があります。αとβの圏B(A, B)における結合を α|β 、fの恒等射はι_f（ギリシャ文字のイオタです）と表します。記号「|」で表される結合演算を縦結合（vertical composition）と呼ぶこともあります。と言えば予測できるでしょうが、後で横結合が出てきます。

横結合演算はこの次

双圏の特徴は、ホム対象が圏であるだけでなく、異なるホム圏に属するセルのあいだに横結合（horizontal composition）が定義されていることです。横結合の話は「その2」でします。