f:A→B を関係圏Relの射だとします。小文字エフだと関数(写像)のような雰囲気ですが、そうではありません。関係圏の射fは、f⊆(A×B) という部分集合です(AとBは集合)。圏の射がいつでも関数だと思い込んだりしてはいけません、そりゃとんでもない誤解ですからね。
関係圏の射、つまり関係(relation)は、定義の上では部分集合ですが、それから関数を導き出すことができます。f⊆(A×B) に対して、f→とf←という関数を定義しましょう。f→とf←は関数(写像)なので集合圏Setの射となり、次のプロファイルを持ちます。ここで、Pow(A) はAのベキ集合です。
- f→:A→Pow(B) in Set
- f←:B→Pow(A) in Set
具体的な定義は:
- a∈A に対して、f→(a) = {y∈B | (a, y)∈f}
- b∈B に対して、f←(b) = {x∈A | (x, b)∈f}
f→(a) は、点aにおけるfの像集合、f←(b) は、点bにおけるfの逆像集合ということです。
関係は、その多重度、出現性、基数などと呼ばれる(すべて同義語)特性で分類されることがあります。これは、像集合 f→(a)、逆像集合 f←(b) のサイズに基づく分類です。集合Xのサイズ(基数、要素の個数)を #(X) として、関係fに対する次の条件を考えます。
- すべての a∈A に対して、#(f→(a)) ≦ 1
- すべての a∈A に対して、#(f→(a)) ≧ 1
- すべての b∈B に対して、#(f←(b)) ≦ 1
- すべての b∈B に対して、#(f←(b)) ≧ 1
これらの条件を満たすfは、それぞれ次のように呼ばれます。:
さて、ここからが本題。上記の単葉、全域、単射的、全射的という特性も持った関係を、矢印の形で区別したいのです。どういう形がいいかな? ということです。関係の特性と矢印の形を結びつける必然的な根拠なんてありません! 恣意的な好みとか雰囲気とか、まーそういう基準しかないから悩むのです。悩んだ結果、現状の案は以下に述べるようなものです。
まず、特別な条件を課さない関係をどう表すか。何の条件もないのだから、プレーンな矢印「→」を使うのも一案です。しかし、写像と関係を区別するため、矢印の先端をカラス足(crow's-foot)と呼ばれる形にする習慣もあります。ここでは、カラス足を採用することにします。
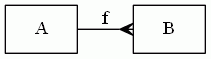
一般の関係では、値 f→(a) が複数個あるかもしれない(0個かもしれない)ので、カラス足でそれを示唆します。
では、プレーンな矢印は何を表すのでしょう? これは部分写像にします。部分写像(partial map)とは、単葉だが全域とは限らない関係です。未定義部分があるかも知れない写像とも言えます。
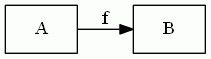
計算(コンピューティング)の文脈では、全域性を保証するのは困難で、たいていは部分写像を扱うことになります。(計算では)一番ありがちなケースがプレーンな矢印となるので、いいんじゃないか、と。
全域で単葉、つまり普通の意味の写像は次のように描くことにします。
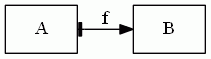
根本の縦棒が全域性の象徴です。部分集合としてのfの“Aへの射影”がA全体になっていることです。
全射性は、部分集合としてのfの“Bへの射影”がB全体になっていることなので、全域性と同じ縦棒を使うことにします。ただし、B側に縦棒です。
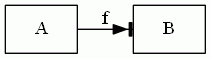
単射に関しては、>→ のような形の矢印を使う例を見たことがあるので:
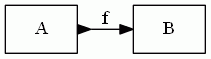
と、ここらへんまではけっこう自然でシンプルなんですが、飾り物を組み合わせるとゴチャゴチャになります。例えば、双射写像(可逆写像)は、全域・単葉で単射的かつ全射的ですから:
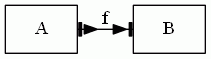
ウーム、暑苦しい。
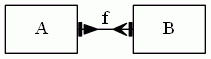
ウーム、ゴージャス過ぎる。
*1:これは、集合B上の分割(partitioning)となる部分集合族があって、その族の添字集合がAとなっている状況です。