昨日・10月13日に、「第三回 物理と情報と幾何のインフォーマルかもな勉強会@スマートニュース株式会社」が開催されました。
長丁場で疲れましたが、聞く側としても大変に面白かったです。まだ刺激が残っていて、忘れないうちに補足を書き残しておきます。
[追記 date="翌日"]お詫びと訂正:佐藤桂さんによるご指摘。トレース付きブレイド圏で、基本ブレイド X+(下の絵の正の交差)を3つ重ねて2本の紐(全部)のトレースを取ると三つ葉結び目(trefoil knot)になると言って、絵も描きました。
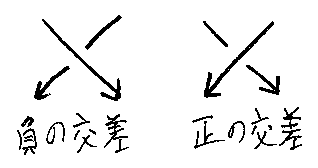
このとき、交差の上下(手前と奥)が逆だったようです。三つ葉結び目は鏡像と同値(アンビエントアイソトピック)にならないので、間違いでした。
他の発表に関して、どれも面白かったのですが、内容を紹介できる能力は僕にはありません。代わりに、飲み会で山田紘頌さんと古賀実さんの会話を聞いていて「へぇー」と思ったことを: 射影空間の部分空間の次元に関して、点を0次元とする派と点を1次元とする派があるとのことです。山田さん0次元派、古賀さん1次元派だそうで。へぇー。[/追記]
[追記 date="2013-11-07"]今頃になってですが; 発表内容のまとめは、次のブログにあります。西尾さんのレポートには発表の内容まで記されています、素晴らしい。
[/追記]
僕(檜山)の話の予定は、「再考: クリーネスター・圏論・計算の離散力学」に書いておきました。いちおう予定のストーリーに沿ったつもりですが、結局は目的である計算には到達せず、「やればたぶん計算できるだろう」という雰囲気まででタイムアウトでした。
でも、「やればたぶん計算できるだろう」という雰囲気が実は大事で、そう思えればあとは実際に計算するだけです。以下に、昨日の復習と、その続きとなる「計算方法の概略」を示します。
復習と計算のヒント
まず、普通の中学校レベルの話として、f(t, x) = t + a・x (・は掛け算)で定義されるfに対して不動点方程式 x = f(t, x) を解きます。このxはパラメータtに依存するので、より正確には、
- x(t) = f(t, x(t))
という形ですね。ちょっと計算すれば、x(t) = (1/(1 - a))・t だとわかります。ここで出てきたtの係数 1/(1 - a) がクリーネスターに相当する量で、実際 1/(1 - a) = 1 + a + a2 + ... = (aのクリーネスター) という無限級数展開を持ちます。収束とかは気にしないことにします。
上記の事実から、クリーネスター a* = 1 + a + a2 + ... の特徴付けが得られます。すなわち、
- 線形不動点方程式 x(t) = t + a・x の解 x(t) の係数が、a* である。
線形関数の係数(比例定数)と線形関数そのものを同一視してもいいので、ちょっと端折った言い方をすれば、
- 線形不動点方程式 x(t) = t + a・x(t) の解 x(t) が、a* である。
と言ってもいいかもしれません。
トレース(対角和ではなくてルーピング)が付いた絵図的行列の圏で考えることにして、f:2→1 (fは、1行2列の行列)のとき、fの不動点は、Tr(f;Δ) で与えられます。ここでΔは対角(コピー)です。絵としては次のようになります。

f† = Tr(f;Δ) と置くと、f† = Δ;(I×f†);f が絵で示せるので、f† はfのパラメータ付き不動点です。fを行列表示すると1行2列の行列なので、f = [b a] と書くとして、f† = [b a]† は1行1列の行列です。特に b =1 のケースを考えて f† = [1 a]† の唯一の成分がaのクリーネスターとなります。なお、[1 a] は、Iを恒等射(単なるヒモ)として (I×a);∇ と書いたほうが絵に忠実です。
以上の話は、スカラーaのクリーネスター a* を、トレースTrを使って定義したことになります。もう一度書くと:
- a* = [1 a]† = Tr([1 a];Δ) = Tr((I×a);∇;Δ)
スラッシュ「/」を改行の代わりに使って縦横配列の行列を書くとして、Δは、[1 / 1] という縦ベクトル(2行1列の行列)なので実際に計算して [1 a];Δ = [1 / 1][1 a] = [1 a / 1 a] となり、
- a* = Tr([1 a / 1 a])
とも書けます。ただし、絵を描く都合からは Tr([1 a / 1 a]) という表式はあまり嬉しくなくて、もとの形 a* = Tr([1 a];Δ) が一番扱いやすい形です。
a+ も当然にトレースで書けて、より対称性が高い形をしています。
- a+ = Tr(∇;a;Δ)
ここまでは、スカラーaに対して a*, a+ をトレースで書いたわけですが、任意の正方行列 f:n→n に対してまったく同様にして a*, a+ をトレースで定義できます。
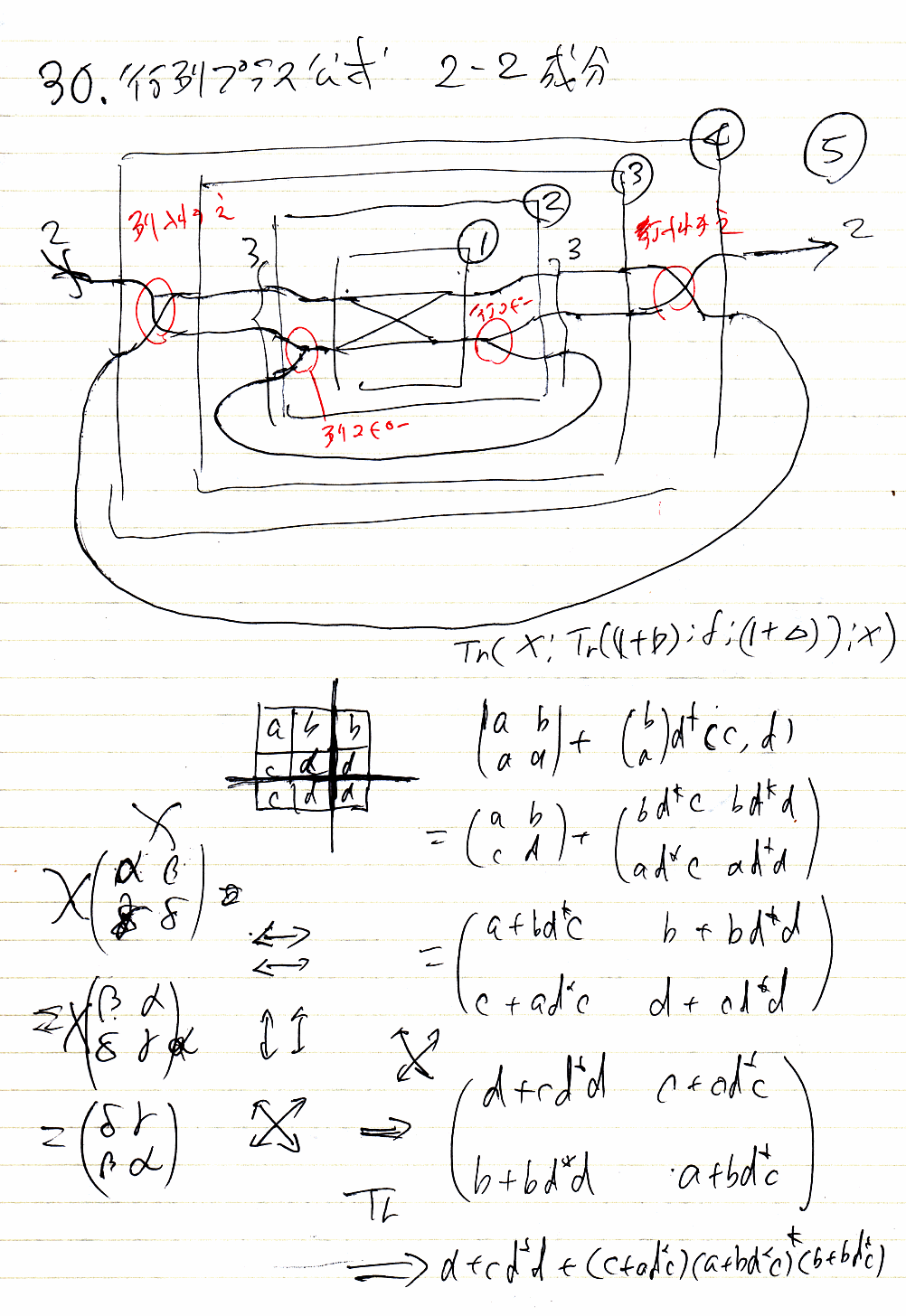
クリーネスター/クリーネプラスがトレースで書けても、トレースが実際に計算できないと先に進めません。f = [a b / c d] のトレースはクリーネスターで書けます。「それじゃ循環論法じゃないか」って? いや大丈夫。2×2行列のトレースがスカラーのクリーネスターで書けるので、次元が下がる方向への“還元”が起きます。結果だけ書いてしまいますが、
- Tr(f) = Tr([a b / c d]) = a + bd*c
という公式が得られます。以下はそこらへんを書いたノート。
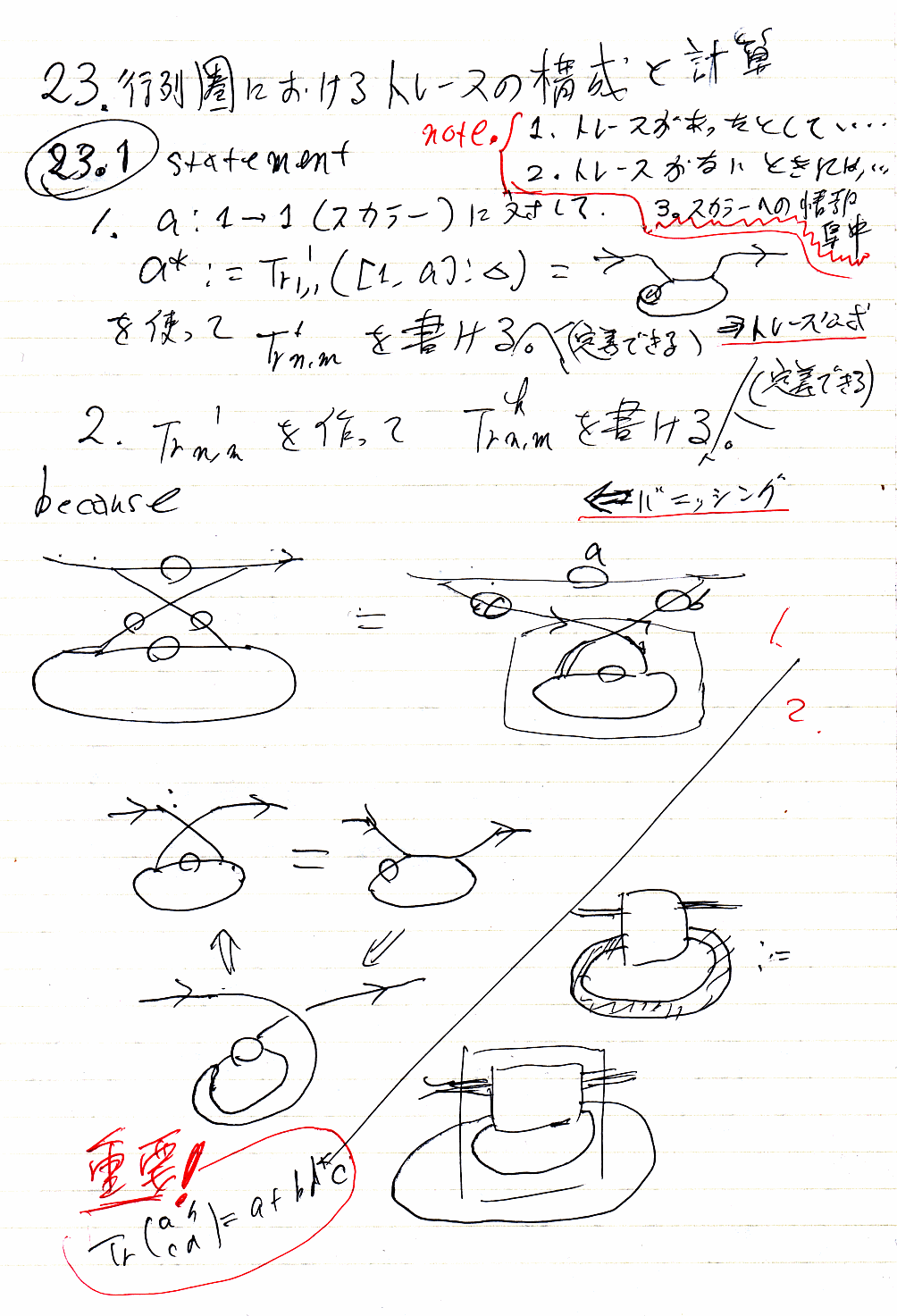
絵で描くなら、スカラーaに対する a*, a+ と、2行2列の行列fに対する f*, f+ は、紐の本数が増える以外の差はありません。下は a+, f+ の絵です。
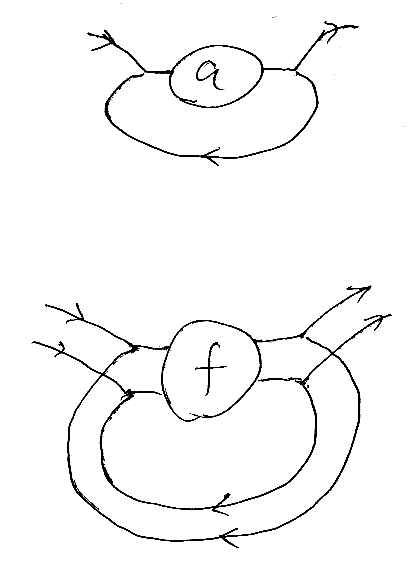
2行2列のf、つまり f = [a b / c d] に対して、f+ = [x y / z w] とすると、4つの成分x, y, z, wは次のように描けます。
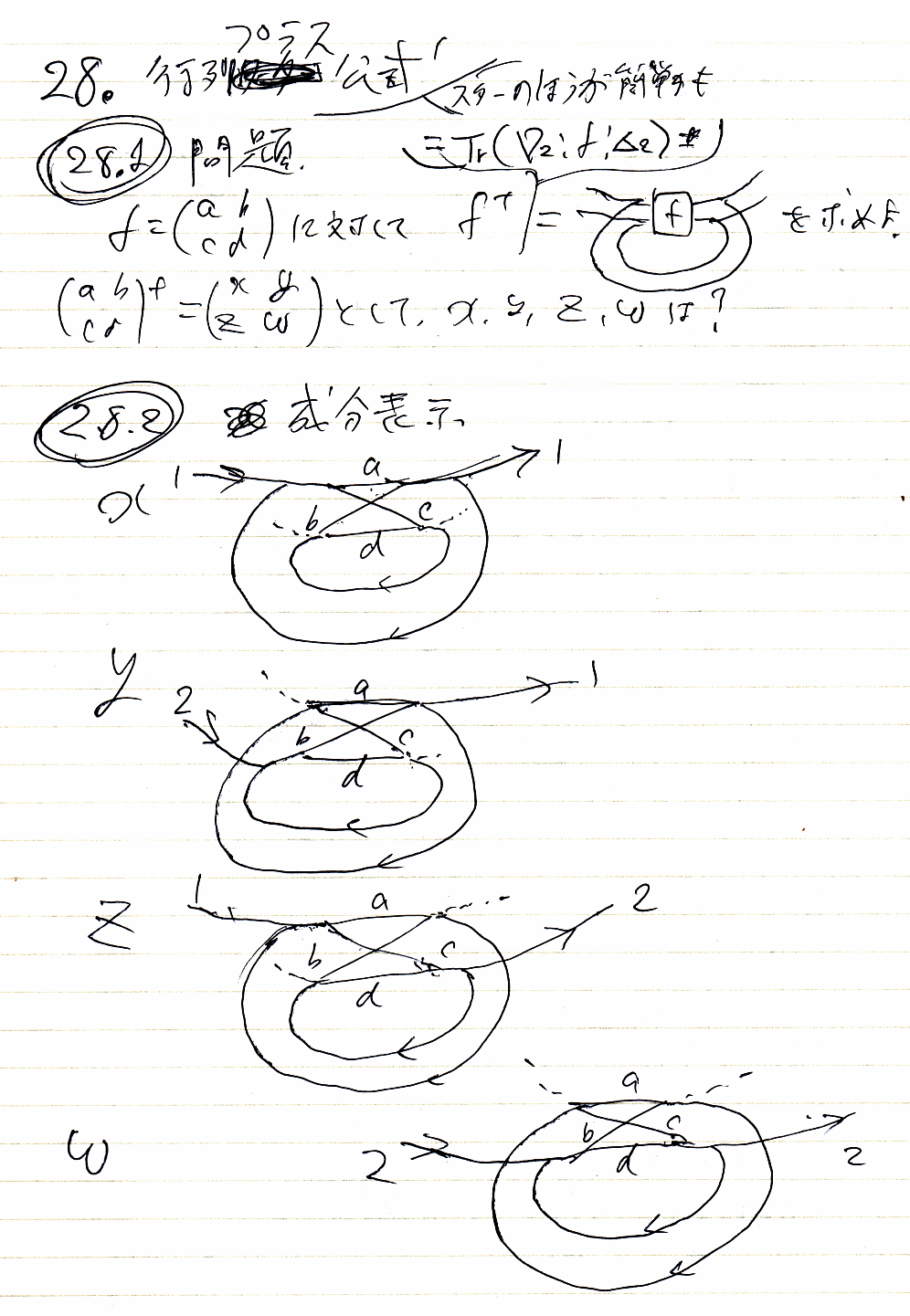
これらを次の処方箋にしたがって計算します。
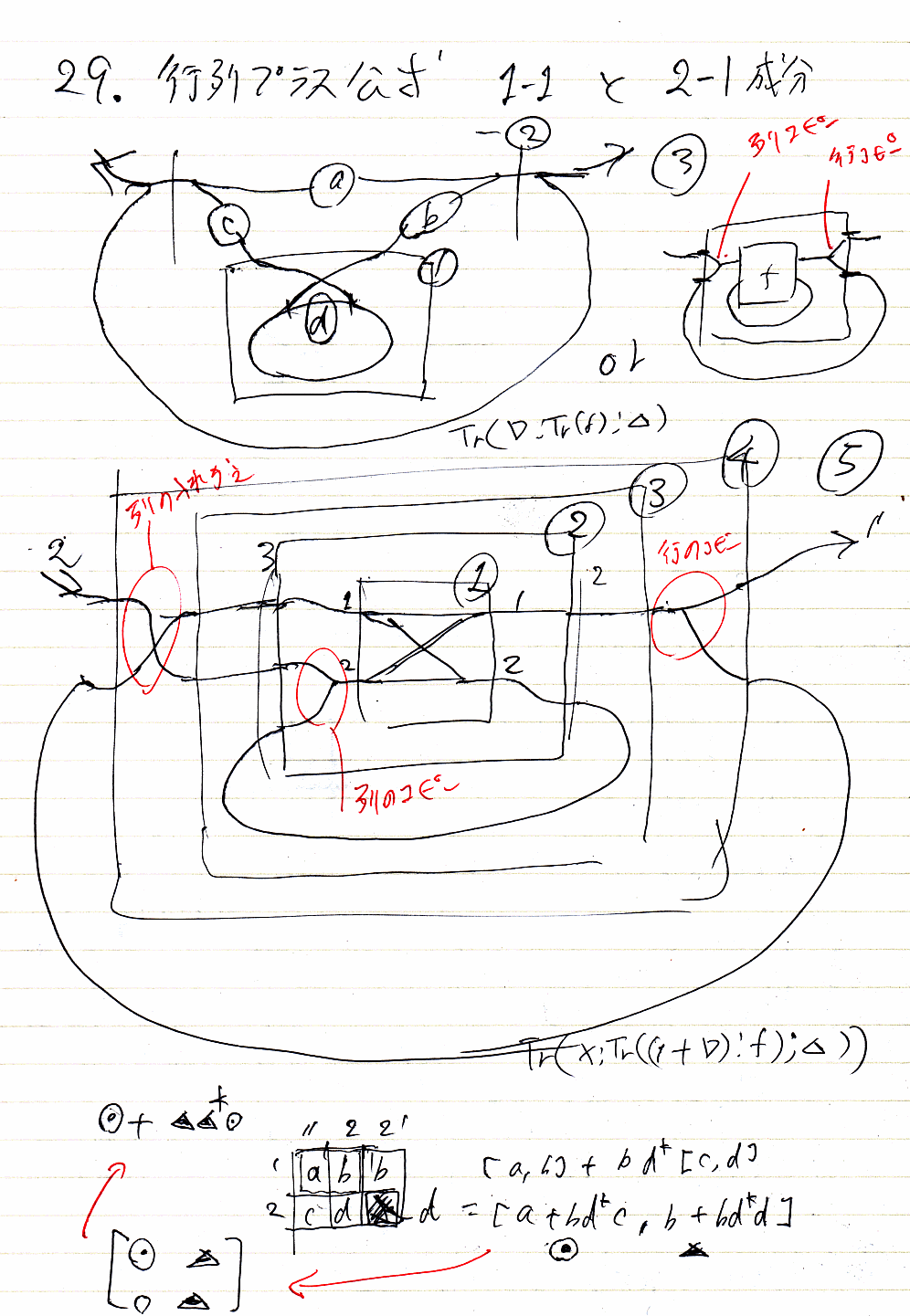
ここで、X(クロス、対称)、Δ(対角、コピー)、∇(余対角、足し算)による掛け算(pre-compose, post-compose)は行列の基本変形に対応しています。[追記 date="2013-10-19"]「27.2. 行の入れ替え(X*)」の右端の絵がオカシイです。ケーブル(2本のワイヤーの束)が交差してますが、これは交差じゃなくて、枝分かれです。[/追記]
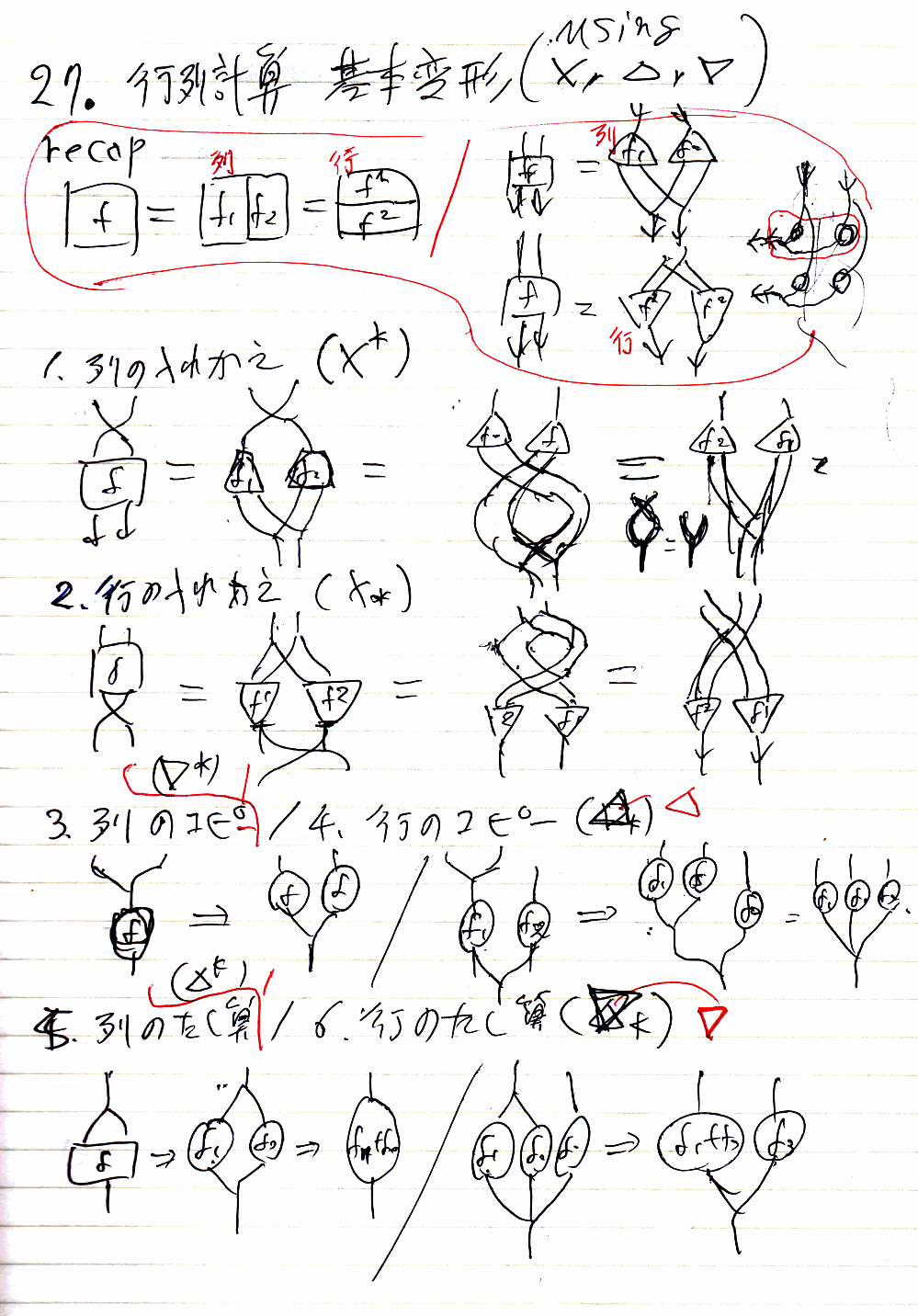
よって、X、Δ、∇が出現したら対応する行列の基本変形を施せばいいことになります。トレースが出てきたら、Tr([a b / c d]) = a + bd*c を使います。頑張れば、f+ の4つの成分x, y, z, w を、a, b, c, dの組み合わせで露骨に書き下せる感じはするでしょう。「組み合わせ」とは、足し算と掛け算、それとスカラーレベルのクリーネスターだけを使った算術式の形ということです。2×2のケースが計算できれば、nに関する帰納的な計算でn×n行列のクリーネスターも書き下せます。
で、答は? 面倒くさいから僕は計算してません。上に挙げたノートのスキャン画像に、計算の一部が入ってますが、あってるか間違っているかはよく分かりません。大きなサイズの行列まで計算するなら、コンピュータに計算させたほうがいいでしょう。
若干の注意
行列と言いながら係数域を特定してないのですが、係数域を前もって指定する必要はありません。圏Cに、X, Δ, !, ∇, i があって、然るべき公理を満たすなら、それからエンドセット C(A, A) (Aは任意の対象)上に半環構造を作れるので、それを係数半環と考えることができます。
一般には、対象Aと半環 C(A, A) を1つに固定することはできませんが、良いセッティングのもとでは、最適なAと C(A, A) を、同型を除いて一意に選ぶことができます。係数とかスカラーとかの概念は普通の行列とのアナロジーとして出しているだけで、特に言及する必要はないくらいです。変動するスカラーも便利に使えます。
圏Cに不動点オペレーター(これも然るべき公理を満たす)があれば、エンドセット C(A, A) はクリーネスターを持つ半環の構造を持ち(クリーネスターは不動点オペレーターから作ります)、その代数構造はコンウェイ代数と呼ばれます。行列圏(より一般には双デカルト圏)では、各エンドセットがコンウェイ代数であることと、圏全体に不動点オペレーターが存ることは同じです。また、デカルト圏という仮定だけでも、不動点オペレーターとトレースの同値性(互いに他を定義可能)が示せます。不動点オペレーターとトレースの同値性がKSHH(カザネスク/ステファネスク/ハイランド/長谷川)定理です。
行列圏を典型とする双デカルト圏という設定のなかでは、トレース、不動点オペレーター、クリーネスター(コンウェイ代数)という構造が同じものであり、なにかの量を計算したいときに、どれを使ってもいいことになります。その一例がクリーネスター/クリーネプラスをトレースを使って計算することです。
そしてそれから
1/(1 - a) = 1 + a + a2 + ... という“等式”は、僕にとってはもの凄く不思議で、なんとか解釈したいとアガイタけど、どうにも分かりません。左辺は引き算と割り算が出てきてますが、半環の文脈ではまったく意味を持ちません。一方、右辺は無限和で、極限や収束がない状況では意味を持ちません。つまり、左右両辺ともに無意味なのに、なんだかソレラシイ、という、何なんだコレ??
形式言語理論の世界では、1/(1 - a) の意味付けが多少はできるんじゃなかろうか? と、漠然とは思っていますが、今のところ、少数の状況証拠とあてにならない夢想のみ。マクノートン/山田の構成法(the McNaughton-Yamada algorithm)やブルゾゾウスキイ導分(Brzozowski derivative)*1を、トレース付き(あるいは不動点オペレーター付き)行列圏でキッチリと定式化できれば、1/(1 - a) に近いナニカを構成できるんじゃないかなー … とか。
状況証拠からは、なにかしら随伴(あるいは共役)作用素の対が潜んでいて、逆作用素はなくても随伴作用素なら在る、という事みたい。もし(希望的予測として)1/(1 - a) と、その無限和展開に随伴的な解釈を与えられたなら、「クリーネスターの計算」の続編にふさわしいトピックになるでしょう。
*1:BrzozowskiのBrはほとんど発音しないで、ゾゾウスキが近いようです(http://ja.forvo.com/word/brzozowski/)
 (
(