昨日の「R言語メタプログラミングのサンプル」に実例として出したRプログラムを見ているうちに、これを手直しして複素関数の可視化が出来るんじゃないか、と思いました。
次元を落として3Dグラフを描く方法と、平面から平面への写像を模様として描く方法を試してみました。
内容:
- 複素関数
- 可視化の方法
- 実例
- 感想など
複素関数
Cは複素数の全体(ガウス平面)とします。D⊆Cを適当な領域として、f:D→C という写像が複素関数ですが、単なる写像ではなくて微分可能(正則)なものを「複素関数」と呼ぶのが普通です。
古典的な記法では、複素関数を w = f(z) (z∈D)のように書きます。虚数単位をiとして、z = x + yi、w = u + vi のような書き方も習慣化しています。習慣に従い、z, w, x, y, u, v は今説明した意味で使うことにします。虚数単位を太字にしたのは、iをインデックスとしても使うからです。
複素関数を可視化する際に、定義域D内に、閉区間の直積となるような矩形 [a, b]×[c, d] を取ります。つまり、[a, b]×[c, d] ⊆ D。さらに、区間[a, b]、[c, d]を、それぞれN等分、M等分して、実数値の増加列を作ります。
- a = x1 < x2 < ... < xN+1 = b
- c = y1 < y2 < ... < yM+1 = d
zi,j := xi + yji と定義すると、zi,j は、(N + 1)行(M + 1)列の行列とみなすことができます。あるいは、(N + 1)×(M + 1)個の複素数からなる集合ともみなせます。集合とみなすときはZという記号を使うことにします。つまり、Z := {zi,j | i = 1, 2, ..., N+1、j = 1, 2, ..., M+1}。
Z⊆D なので、zi,j∈Z に対して wi,j := f(zi,j) を定義できます。図示の対象となるのは、w平面の点達 wi,j (i = 1, 2, ..., N+1、j = 1, 2, ..., M+1)です。
可視化の方法
w = f(z) の可視化の方法は2種類試してみました。
- z平面の方眼(格子)の像を、w平面における模様として描く。
- wの値から単一実数を取り出して、3Dグラフを描く。
ニ番目の3Dグラフの方法では、複素数wから実数の取り出し方が4種類あるので、細分すると5種類の描き方があります。
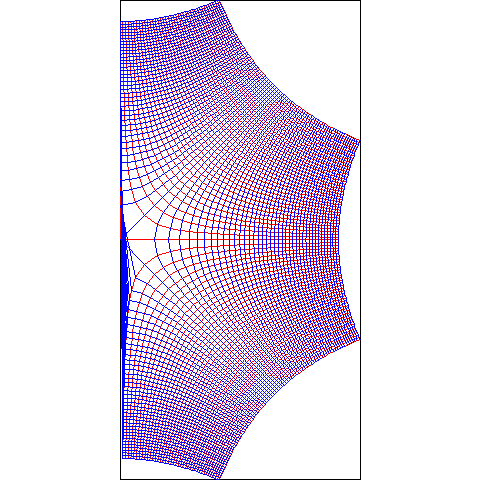
一番目の方法は仮に写像図と呼んでますが、この方法が描画関数のデフォルトで、drawComplex(z^2) とすると次の図を描きます。
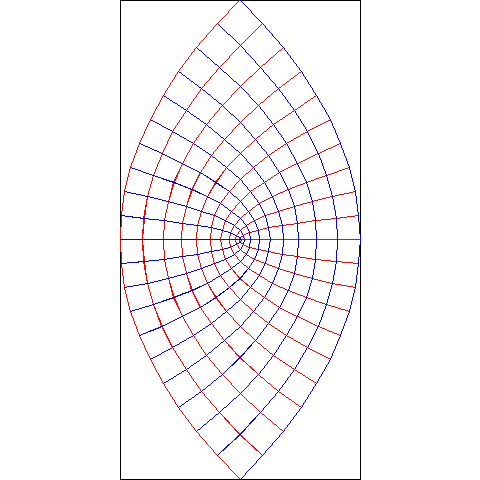
これは、z平面にあった次のようは方眼(網目)がw平面に写って描く模様です。
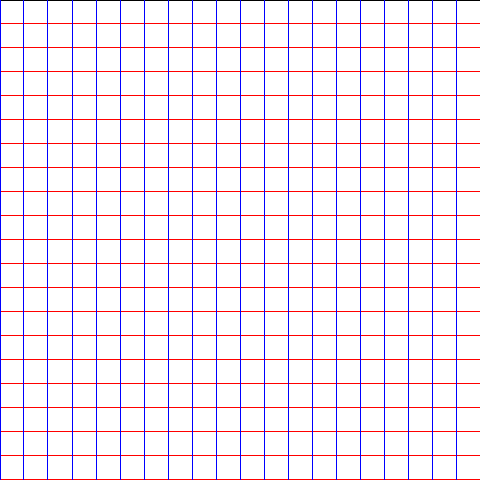
z平面内における縦横の直線の交点(格子点)が、先に説明した集合Zです。w平面の点達f(Z)と曲線群による模様が w = f(z) の写像図です。
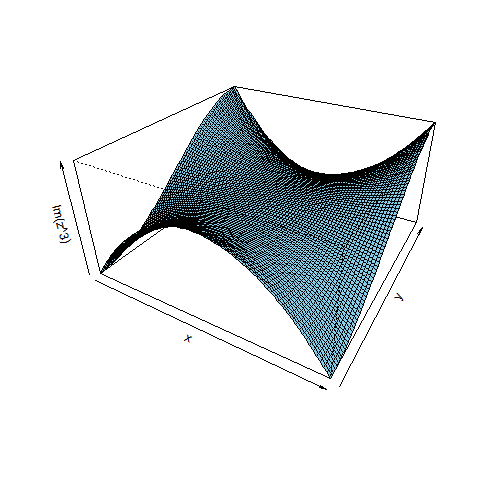
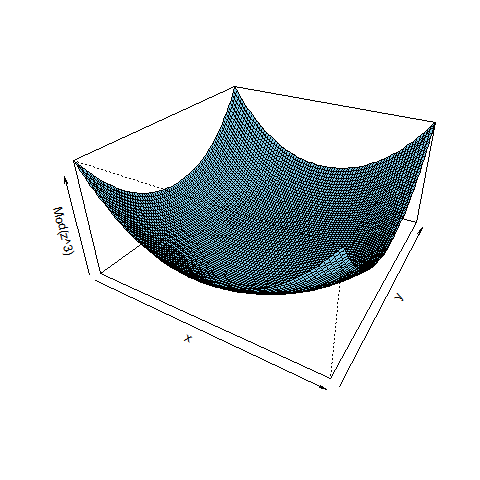
3Dグラフのほうは、Re(f(z)), Im(f(z)), Mod(f(z)), Arg(f(z)) の4種の値を3Dグラフに描きます。それぞれの意味は:
- f(z) の実部
- f(z) の虚部
- f(z) の絶対値
- f(z) の偏角
実例
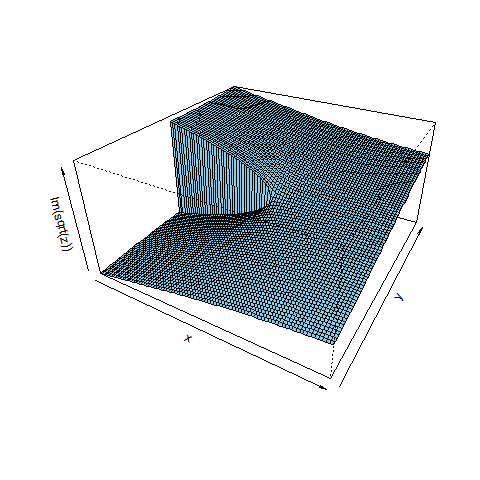
w = z^3 (3次関数)と w = sqrt(z) (平方根関数)を描いた図を示します。drawComplex(関数の式, 描画方法, xdiv = 80, ydiv = 80) を呼び出した結果です。デフォルトの区間[-1, 1]を80等分しています。4つの3Dグラフは、左上:実部、右上:虚部、左下:絶対値、左下:偏角 です。
3次関数 w = z^3
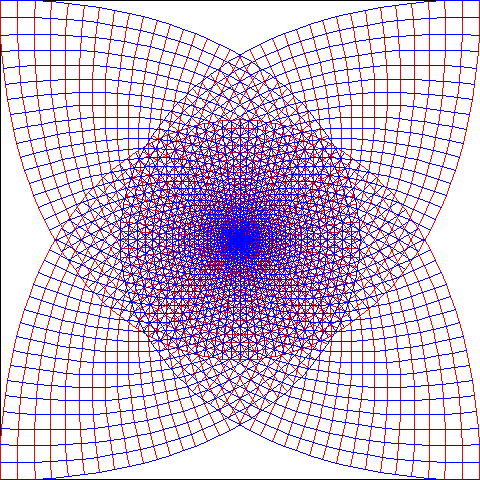
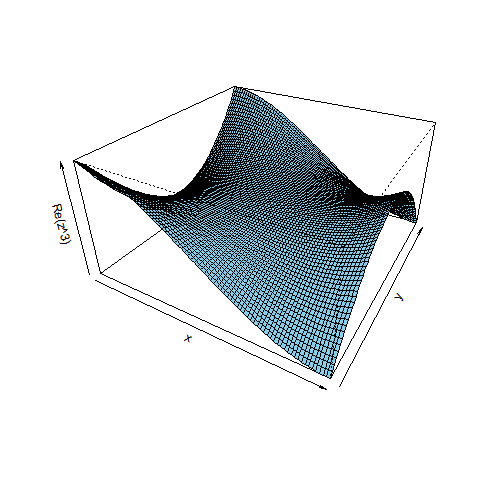 |
 |
 |
 |
平方根関数 w = sqrt(z)
 |
 |
 |
 |
感想など
ワンライナーですぐに複素関数を図示できるので、なかなか便利です。「えっ、この関数はこんな形だったの」と意外だったりして、面白いです。それでも、2次元→2次元 の写像をイメージするのは難しいですね。
Rは組み込みのデータ型として複素数をサポートしているので、複素関数を扱うのはとても簡単です。何も意識しなくていいと言っていいでしょう。加減乗除はもちろん、指数関数、対数関数、三角関数、逆三角関数、双曲線関数などは、複素数を引数にしてちゃんと動きます。これは素晴らしい。
惜しむらくは、Rにアニメーション機能が備わってないことです。ライブラリを使ってアニメーション出来なくはない(「Rで離散力学系のアニメーションを作ってみた」参照)ですが、面倒で機能貧弱です。時間方向が使えると、表現の幅が格段に拡がるのですが。
以下にソースコード、「R言語メタプログラミングの基礎」で定義した2つのユーティリティ関数noDefault()とmakeFunction()が必要です。
[追記]ソースコードはgistにも貼り付けてあります。
以下のコードは変更する気はありませんが、gistのほうは変更するかも知れません。[/追記]
# drawComplex.R # gridパッケージが必要 if (!require('grid')) { install.packages('grid') stopifnot(require('grid')) } # noDefaultとmakeFunctionが必要 stopifnot(exists("noDefault") && is.function(noDefault)) stopifnot(exists("makeFunction") && is.function(makeFunction)) # 複素関数の値(wの値)を成分とする複素数マトリックスを作成し、関連情報と共に返す makeXyzw <- function ( # 複素関数の式、コールオブジェクトを渡す expr, # 複素変数の名前、文字列で指定する varname = "z", # 複素変数のガウス平面(x-y-座標)における描画対象域 xlim = c(-1, 1), ylim = c(-1, 1), # 描画対象域のx,y方向を幾つの少区間に分割するか(分割数) xdiv = 20, ydiv = 20) { x0 <- xlim[1] x1 <- xlim[2] y0 <- ylim[1] y1 <- ylim[2] xStep <- (x1 - x0)/xdiv yStep <- (y1 - y0)/ydiv xBreaks <- seq(from = x0, to = x1, by = xStep) yBreaks <- seq(from = y0, to = y1, by = yStep) # 関数の仮引数リストの作成 fplist <- list(noDefault()) # デフォルト値なし1変数 names(fplist) <- c(varname) # 引数名(複素独立変数名)を指定 # 関数の作成 fun <- makeFunction(fplist, expr) wMatrix <- matrix(NA, xdiv + 1, ydiv + 1) for (i in 1:(xdiv + 1)) { for (j in 1:(ydiv + 1)) { wMatrix[i, j] <- fun(xBreaks[i] + yBreaks[j]*1i) } } # 参考のために独立変数zのマトリックスも添える zMatrix <- outer(xBreaks, yBreaks, function(x, y) x + y*1i) list( xlim = xlim, ylim = ylim, xStep = xStep, yStep = yStep, x = xBreaks, y = yBreaks, z = zMatrix, w = wMatrix ) } # 複素関数を描く # 描画方法:"map", "re", "im", "mod", "arg" # map : 写像図、x方向/y方向の直線群に対する像曲線群を描く # re : 値の実部を描く # im : 値の虚部を描く # mod : 値の絶対値を描く # arg : 値の偏角を描く drawComplex <- function ( # 複素関数の式、引数としてzの式を書く expr, # 描画方法、シンボルでもよい way = "map", # 複素変数のガウス平面(x-y-座標)における描画対象域 xlim = c(-1, 1), ylim = c(-1, 1), # 描画対象域のx,y方向を幾つの少区間に分割するか(分割数) xdiv = 20, ydiv = 20, # perspのオプション theta = 30, phi = 30, expand = 0.5, col = "skyblue", # 関数の情報を戻り値として出力するか output.info = FALSE ) { # 引数の式を評価せずに取り出す expr <- substitute(expr) # way引数の取得とチェック way <- substitute(way) stopifnot(is.name(way) || is.character(way)) way <- as.character(way) stopifnot(any(c("map", "re", "im", "mod", "arg") == way)) # 関数値のマトリックスを作成する xyzw <- makeXyzw(expr, varname = "z", xlim = xlim, ylim = ylim, xdiv = xdiv, ydiv = ydiv ) # 基本的なパラメータをセット w <- xyzw$w ulim <- range(Re(xyzw$w)) vlim <- range(Im(xyzw$w)) rangeWidth <- ulim[2] - ulim[1] rangeHeight <- vlim[2] - vlim[1] rangeSize <- max(rangeWidth, rangeHeight) u0 <- ulim[1] v0 <- vlim[1] if (way == "map") { # 写像図による描画 # 使用する変数: w, u0, v0, rangeSize, rangeWidth, rangeHeight uOffset <- (rangeSize - rangeWidth)/(2*rangeSize) vOffset <- (rangeSize - rangeHeight)/(2*rangeSize) grid.newpage() grid.rect(width = rangeWidth/rangeSize, height = rangeHeight/rangeSize) # x方向直線の像曲線 for (j in 1:(ydiv + 1)) { u <- Re(w[ ,j]) v <- Im(w[ ,j]) grid.lines((u - u0)/rangeSize + uOffset, (v - v0)/rangeSize + vOffset , gp = gpar(col="red")) } # y方向直線の像曲線 for (i in 1:(xdiv + 1)) { u <- Re(w[i, ]) v <- Im(w[i, ]) grid.lines((u - u0)/rangeSize + uOffset, (v - v0)/rangeSize + vOffset, gp = gpar(col="blue")) } } else { # perspによる3Dグラフ描画 # 使用する変数: way, x, y, w, xlim, ylim funName <- paste(toupper(substr(way, 1, 1)), substr(way, 2, 10), sep="") fun <- eval(as.name(funName)) # perspの引数リストを作成する args <- list( x = xyzw$x, y = xyzw$y, z = fun(xyzw$w), xlab = "x", ylab = "y", zlab = paste(funName, "(", deparse(expr), ")", sep=""), xlim = xlim, ylim = ylim, theta = theta, phi = phi, expand = expand, col = col ) # persp関数の呼び出し do.call("persp", args) } # 情報の出力(オプショナル) if (output.info) { return( list ( xlim = xlim, ylim = ylim, ulim = ulim, vlim = vlim, rangeRect = list( left = u0, bottom = v0, width = rangeWidth, height = rangeHeight ) ) ) } }