新しい絵算手法：ストリング＋ストライプ図 - 檜山正幸のキマイラ飼育記 (はてなBlog)

ここ数日、新しい絵算〈{pictorial | graphical | diagrammatic} calculation〉を考えて試しているんですけど、けっこう使えそう。新しいとは言っても、本質的に新しいものではなくて、既存の2つの描画法を組み合わせたものです。ストリング図とストライプ図のハイブリッドなので、ベタにストリング＋ストライプ図〈string+stripe diagram〉と呼んでます。メインはストライプ図なので、ストリング図機能を取り込んだストライプ図とも言えます。

内容：

“モノイド圏の圏”における3つの方向
3次元見取り図
正面図：ストライプ図
側面図：ストリング図
例題のサワリ
おわりに

“モノイド圏の圏”における3つの方向

2つのモノイド圏とそのあいだの関手を扱うと、射の結合の方向、モノイド積の方向、関手の結合方向の3つの方向が出てきます。3次元の見取り図を描けばいいのですけど、これは手間がかかる！それで、側面図としてストリング図、正面図としてストライプ図を使うことにします。

このとき、「射の結合方向を縦（上から下）、関手の結合方向を横（左から右）に見る」のが側面で、「射の結合方向を縦（上から下）、モノイド積の結合方向を横（左から右）に見る」のが正面とします。自然変換に関しては、縦結合の方向＝射の結合方向、横結合の方向＝関手の結合方向です。

3次元見取り図

実例を出さないとピンとこないでしょう。次の絵は、モナド乗法とテンソル強度の組み合わせの3次元見取り図です。

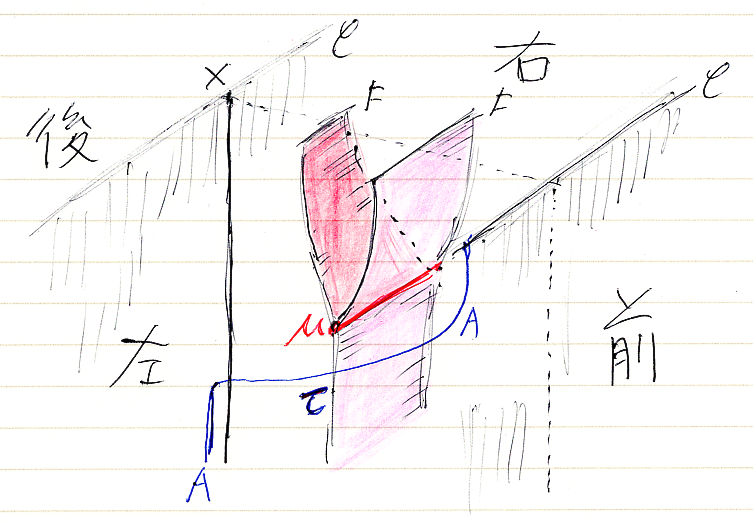
C = (C, $\otimes$ , I) がモノイド圏で、F = (F, μ, η, τ) はモノイド圏C上の強モナド〈strong monad〉とします。τはテンソル強度〈tensorial strength〉で、A, X∈|C| でインデックスされた射の族（自然変換）です。

τ_A,X:A $\otimes$ F(X)→F(A $\otimes$ X)

3次元での絵の描き方は：

圏Cは壁のような平面とする。
Cの対象は、平面内を縦に走るワイヤー
Cの射は、平面内のノード（上の絵には登場しない）
関手（の断片）は、2枚の平面のあいだに在るストライプ（リボン）

関手の結合方向は、後（奥）から前（手前）の方向とします。関手 F:C→C は、奥側にあるC平面から手前のC平面のあいだに在ります。F*F:C→C なら、Fのストライプを2枚並べて置くことになります。モナド乗法 μ::F*F⇒F:C→C は、2枚のストライプ（リボン）を1枚に融合する操作で、μを赤い縫い目で表しています。

テンソル強度は、手前のC側で対象Aを左から掛ける操作を、奥のCでの掛け算操作に変換します。このことを、手前の青ワイヤーが奥の青ワイヤーへと移動しているように描いています。縦方向は、射の結合方向／自然変換の縦結合方向ですが、同時に操作が実行される時間方向だとも解釈するといいでしょう。

正面図：ストライプ図

上記の状況を、手前から見て描いた正面図が次です。正面からの観察者は、関手の結合方向が自分に向かって来る位置から見ているとします。

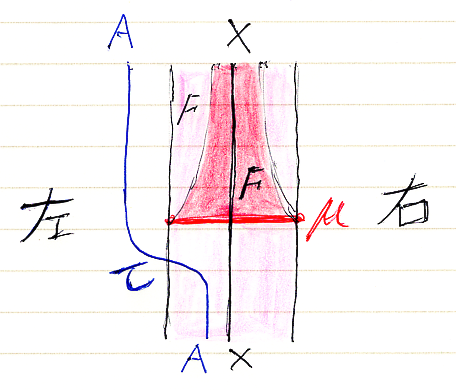
関手を表すストライプは半透明だとして、奥のストライプは細い幅にします。奥から順に、対象X、一番目のF、二番目のFが入れ子に見えます。対象Aの左掛け算は、青いワイヤーを左に併置するだけです。青いワイヤーがストライプを突き抜けている箇所がテンソル強度と解釈します。ストライプの内側に入った青いワイヤーは、奥のC側での掛け算とみなされます。

側面図：ストリング図

同じ状況を側面から見てみます。ただし、3次元見取り図をそのまま横側から写生するのではなくて、ストリング図の流儀による多少の描き換えが発生します。

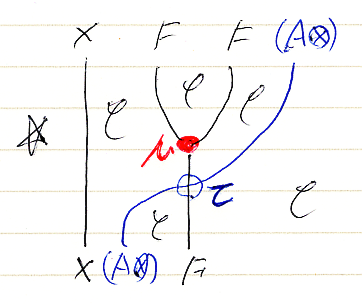
ストリング図における圏は、平面（を側面から見た直線）ではなくて領域です。
ストリング図における対象は、自明圏☆からの関手として表します。（例： X）
ストリング図における掛け算（モノイド積）は、スタンピング関手として表します。（例： (A $\otimes$ )）

このような“流儀”の違いがあるものの、ストライプ図とストリング図を併用すると、3次元的な状況を把握しやすくなります。

例題のサワリ

例題として*1、モノイド圏 C = (C, $\otimes$ , I) 上の強モナド F = (F, μ, η, τ) から、対象 N = F(I) に載ったモノイド N = (N, m, e) を構成することを考えます。

単位対象Iでの値F(I)の上に、μ, ηから誘導されたモノイド構造が載ることは、直感的には“いかにも”なのですが、どう計算していいかハッキリしません。ストリング＋ストライプ図だと、F(I)上のモノイド構造を比較的楽に構成できます。次の図は、N = F(I) 上のモノイドの結合律を示す図です。

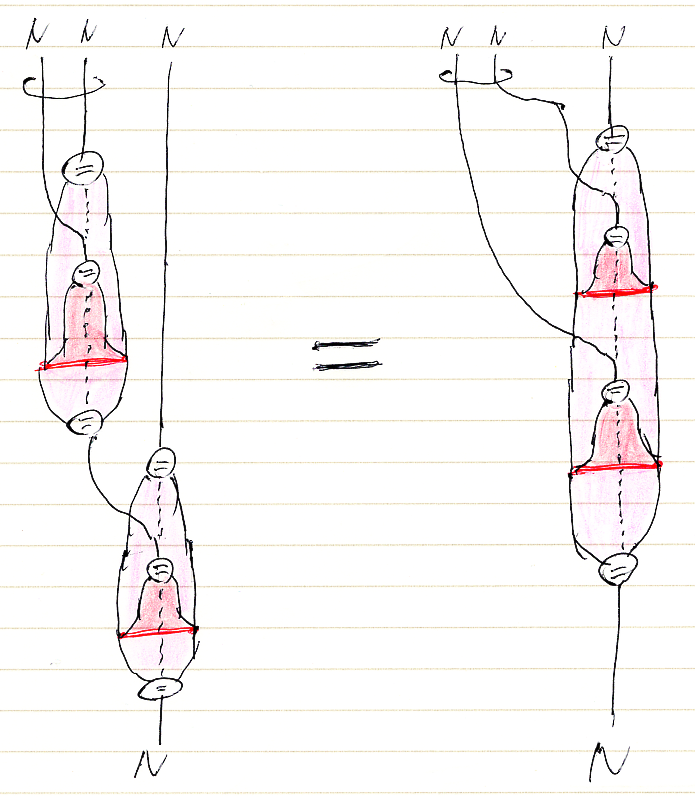
この図をしばらく眺めていると、左辺から右辺へ（あるいは逆方向）の変形過程のアニメーションムービーが見えてきます。ムービーの各フレーム〈スチル | コマ〉を時間順に並べれば、求める結合律の証明が得られます。

今日は、証明＝変形操作の詳細は割愛しますが、図の各部の意味は次のようです。

2本のNを囲んでいる糸は、 (N $\otimes$ N) $\otimes$ N の括弧に相当し、(N $\otimes$ N) $\otimes$ N→N $\otimes$ (N $\otimes$ N) で糸は右に移動します（移動後の糸を描き忘れているけど、まーいいでしょ）。
'='が書いてあるノードは、明示的等号ノード〈explicit equality nodes〉で、N = F(I) または F(I) = N を示します。
ピンクまたは赤のストライプは、関手 F:C→C を表します。
点線は、単位対象Iです。
N $\otimes$ I→N は、右単位律子〈right unitor〉ρ_Nです。
赤い横線は、モナド乗法 μ::F*F⇒F:C→C です。
モノイドの乗法 m:N $\otimes$ N→N は、τ_N:N $\otimes$ F(I)→F(N $\otimes$ I), F(ρ_N):F(N $\otimes$ I)→（F(N) = F(F(I))）, μ_I:F(F(I))→（F(I) = N）の縦結合で定義されます。