このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

ド・ラーム・コホモロジーとホッジ分解のオモチャ (2/2)

雑記／備忘

「ド・ラーム・コホモロジーとホッジ分解のオモチャ (1/2)」の続き・後編です。今回の第2節から第6節（全8節）で、オモチャ＝有限離散モデルを作ります。この部分は、純粋に線形代数の話です。ここだけを取り出して（文脈を無視して）、線形代数の練習問題として読むこともできます。第7節で、前回の話との関係を述べます。「背景を知らずに代数的議論だけを追うのはイヤだ」という方は、第7節を先に読んでください。

内容：

前回・前編の内容：

  1. 予備知識は線形代数だけ
  2. 背景のオハナシ（超・急ぎ足）
  3. 複体
  4. 複体上のパスとチェーン
  5. 実数係数チェーン空間
  6. 境界作用素 1
  7. 境界作用素 2
  8. 組み合わせ複体と代数的複体
  9. 代数的複体もっと
  10. ラプラシアンとラプラス方程式

この記事の記述方法について

この節には、僕からの注意とお願いが含まれます。

記事内で述べられている命題のあいだの関係をハッキリさせるために、命題にラベルを付けることにします。例えば：

  • [記述サンプル] (a + b) + c = a + (b + c) ---(足し算の結合法則)

この例では、「足し算の結合法則」というラベルが導入されています。ラベル付けされた命題を参照するときは、「$(ラベル)」と書くことにします。

  • [記述サンプル] $(足し算の結合法則)によりウンヌンカンヌン

参照からもとの命題にハイパーリンクを張ったりすると便利でしょうが、そこまではやってません。文字列検索で、もとの命題は探せるでしょう。

命題をラベルにより参照したとき、その命題を繰り返し記述（引用）するときは、次に形にします。

  • [記述サンプル] $(足し算の結合法則: (a + b) + c = a + (b + c) )によりウンヌンカンヌン

一時的なラベルには番号（「---(1)」や「$(1)」）を使います。

記事本文内で言及してないが、予備知識だと想定されている命題への参照は、「$?(ラベル)」とします。

  • [記述サンプル] $?(ピタゴラスの定理)によりウンヌンカンヌン

この場合、「ピタゴラスの定理」というラベルが記事本文内にあるわけではありません。必要があれば、ラベルの文言をヒントに何かで調べてください。

こういうルールで書き進めてみると、問題が発生しました。命題のラベルにそれらしい語句を割り当てようとすると、本文内で説明してない言葉が入り込んでしまうのです。例えば、「ヌルベクトル」について一切説明してないにも関わらず、ラベルは「非自明ヌルベクトルの非存在」となったりします（実際、このラベルを使っています）。それで、ラベル内の文言を脚注で説明しだしたのですが、いちいちこれをやっていると、脚注が増えて大変。

ラベルを、通し番号やランダム文字列にすればこの問題は発生しませんが、それも味気ないし、ラベルを記憶できません。それでお願いです。ラベルの意味が分からなくても詮索しないでください。識別用の文字列に過ぎない、と割り切ってください。よろしくお願いします。

ラベルが付いている命題を、この記事内ですべて証明しているわけではありません。が、要点となる目ぼしい命題には証明を付けています。僕は、説明（地の文）に証明を埋め込むスタイルが好きなんですが、それが苦しいときは別枠で証明を書きます（けっこう別枠が多い）。

あ、それと； 僕の横着から、F;Gのような図式順記法と、G\circFのような反図式順記法が混じっています。それを不快と感じたり困惑してしまう方は、「双対や随伴に強くなるためのトレーニング」を読んでトレーニングしてくださいな。

内積ベクトル空間と随伴線形写像

Vは実数係数ベクトル空間で、内積〈inner product〉が備わっているとします。u, v∈V に対して、uとvの内積を(u|v)と書きます。内積は双線形（uに関してもvに関しても線形）な実数値関数で、次を満たすものです。

  1. (u|v) = (v|u) ---(内積の対称性)
  2. (v|v) ≧ 0 ---(内積の正定値性)
  3. (v|v) = 0 ならば v = 0 ---(非自明ヌルベクトル*1の非存在)

次の事実は、定義からすぐに出ますが、重要です。

  • (任意の u∈V に対して (u|v) = 0) ⇔ v = 0 ---(内積の非退化性*2)

ここから先、ベクトル空間は有限次元のものだけ考えます。ベクトル空間Vが内積を持つとき、正規直交枠 {a1, ..., an} （ai∈V）が取れます。枠〈frame〉とは、基底の要素に番号（全順序）を付けたものです*3。{a1, ..., an} の双対枠を {f1, ..., fn} としましょう。双対枠は、Vの双対空間 V* = (V上の線形形式の空間) の枠となります。双対枠の要素fjは、次のように定義されます。

  • i = 1, ..., n に対して、fj(ai) := δji ---(双対枠の定義)

ここでδjiはクロネッカーのデルタで、

  • δji := (if i = j then 1 else 0)

aiをｆiに対応させる写像を線形に拡張して Φ:V→V* が定義できます。このΦは、実は正規直交枠の取り方に寄りません。正規直交枠を使わずいきなりΦを定義するなら、

  • Φ(u)(v) := (u|v) ---(カリー化内積の定義*4)

あるいはラムダ記法を用いて、

  • Φ(u) := λv.(u|v)

と定義します。Vが有限次元でないと、このΦが全射であることは自明ではありません（リースの表現定理など）。今は有限次元での話なので、Φが（ベクトル空間の）同型写像なのは容易にわかります。

V, Wが2つの内積ベクトル空間〈inner product vector space〉（内積が備わったベクトル空間）だとして、F:V→W を線形写像だとします。Fの随伴線形写像〈adjoint linear map〉F†を次のように定義します。

  • F† := Φ;F*;Φ-1 :W→V ---(随伴線形写像の定義)

ここで：

  • ';'は、“写像の結合”の図式順〈diagrammatic-order〉記号です。反図式順〈anti-diagrammatic-order〉記号'\circ'を使うなら、F† := Φ-1\circF*\circΦ 。
  • 図式順記法で左のΦはWに対する Φ = ΦW :W→W* で、右のΦ-1はVに対する Φ-1 = (ΦV)-1 :V*→V です。つまり正確に書けば、F† := ΦW;F*;(ΦV)-1 。
  • F*はFの双対線形写像〈dual linear map〉で、(F*(g))(v) := g(F(v)) として定義されます。

F†は次の性質を持ちます。

  • 任意の v∈V, w∈W に対して、(F(v)|w) = (v|F†(w)) ---(随伴線形写像の基本性質)

この性質を持つような（唯一の）線形写像としてF†を特徴付けることもできます。記法の工夫（すぐ下の箇条書き）の例示も兼ねて、実際に計算しておきましょう。

  1. f∈V*, v∈V に対して、f(v)を<f|v>とも書く。
  2. F;G = G\circF を単に FG と書いてよい。
  3. F(v) を単に Fv と書いてよい。
  4. 結合（写像の合成、記号は'\circ', ';', 併置）よりも、単項演算子のスター(-)*、ダガー(-)†のほうが優先される。
  5. V** = (V*)* をVと同一視して、Φ:V→V* の双対を Φ*:V→V* とみなす。この設定で、F** = (F*)* = F, Φ* = Φ, (Φ-1)* = Φ-1 。
ターゲット命題： (F(v)|w) = (v|F†(w)) ---(随伴線形写像の基本性質)

内積(-|-)を、Φと<-|->で表すなら、
$(随伴線形写像の基本性質: (F(v)|w) = (v|F†(w)) )は
  <ΦFv|w> = <Φv|F†w> ---(1)
と同値なので、$(1)を示せばよい。

$(1: <ΦFv|w> = <Φv|F†w> )を示す。

先に、(F†)* を計算しておく。
    (F†)*
// $(随伴線形写像の定義)により
  = (ΦV-1F*ΦW)*
// $?(双対を取るスター・オペレーターの性質)により
  = ΦW*F**(ΦV-1)*
// F** = F, Φ* = Φ, (Φ-1)* = Φ-1 を使って
  = ΦWFΦV-1
よって、
  (F†)* = ΦWFΦV-1
簡略に書けば
  F†* = ΦFΦ-1 ---(2)

次に、目的の等式$(1)を示す。
    <Φv|F†w>
// $?(双対線形写像の性質)から
  = <(F†)*Φv|w>
// 先に計算した $(2: F†* = ΦFΦ-1 )を使って
  = <(ΦFΦ-1)Φv|w>
// Φ-1Φ を消して
  = <ΦFv|w>
よって、
  <ΦFv|w> = <Φv|F†w>

$(1)が示せた。

正規直交枠を使って行列表示すると、F*もF†も、Fを表す行列の転置行列で表示できます。このため、F*とF†は混同／同一視されがちですが、ここでは区別してください。F*とF†では、写像としてのプロファイル（域と余域）が違います。

  • F*:W*→V*
  • F†:W→V

線形写像にその随伴線形写像を対応させるダガー・オペレーター(-)†は、次のような法則を満たします。

  1. (F†)† = F ---(ダガーの対合性)
  2. (F;G)† = G†;F† または (G\circF)† = F†\circG† ---(ダガーの反変性)
  3. (idV)† = idV ---(恒等のダガー)
  4. (0V,W)† = 0W,V （0V,Wは、V→W のゼロ写像） ---(ゼロ射のダガー)

部分空間の直交性と直交補空間

Vを有限次元内積ベクトル空間だとして、S, TなどはVの部分ベクトル空間〈部分空間〉だとします。次の定義の右辺が成立するとき、SとTは直交している〈orthogonal〉といい、S⊥T と書きます。

  • S⊥T :⇔ 任意の u∈S, v∈T に対して、(u|v) = 0 ---(空間の直交の定義)

部分空間Sに対して、Sの直交補空間〈orthogonal complement〉S⊥ は次のように定義します。

  • S⊥ := {v∈V | 任意の s∈S に対して、(s|v) = 0} ---(直交補空間の定義)

定義からすぐに次が言えます。

  1. S⊥はVの部分空間である。 ---(直交補空間の部分空間性)
  2. S⊥S⊥ ---(部分空間と直交補空間は直交)
  3. S⊥T ⇒ S∩T = {0} ---(直交する空間の共通部分)
  4. S⊥T ⇔ S⊆T⊥ ⇔ T⊆S⊥ ---(直交の言い換え)

Vの部分空間S, Tに対して、S∧TとS∨Tを次のように定義します。

  • S∧T := S∩T （集合の共通部分） ---(ミート空間の定義)
  • S∨T := {v∈V | s∈S と t∈T により、v = s + t と書ける} ---(ジョイン空間の定義)

S∧TとS∨Tの定義に内積は関係ありませんが、内積があると、次の法則が言えます。

  • (S∨T)⊥ = S⊥∧T⊥ ---(直交補空間 ド・モルガンの法則 1)
  • (S∧T)⊥ = S⊥∨T⊥ ---(直交補空間 ド・モルガンの法則 2)

これは、論理におけるド・モルガンの法則と同じ形です。“ド・モルガンの法則”の1番目の半分 (S∨T)⊥ ⊆ S⊥∧T⊥ だけ示すと：

ターゲット命題： (S∨T)⊥ ⊆ S⊥∧T⊥

  v∈(S∨T)⊥ と仮定する。
$(ジョイン空間の定義)と$(直交補空間の定義)から
  任意の s∈S, t∈T に対して、(v|s + t) = 0
$?(内積の双線形性)から
  任意の s∈S, t∈T に対して、(v|s) + (v|t) = 0 ---(1)
t = 0 でも$(1)は成立するから
  任意の s∈S に対して、(v|s) = 0 ---(2)
s = 0 でも$(1)は成立するから
  任意の t∈T に対して、(v|t) = 0 ---(3)
$(2)を言い換えると
  v∈S⊥ ---(4)
$(3)を言い換えると
  v∈T⊥ ---(5)
$(4), $(5)から
  v∈(S⊥∧T⊥)
以上より
  v∈(S∨T)⊥ ⇒ v∈(S⊥∧T⊥)
vは任意だったから
  ∀v.(v∈(S∨T)⊥ ⇒ v∈(S⊥∧T⊥))
つまり
  (S∨T)⊥ ⊆ S⊥∧T⊥

対偶の法則に相当する次も成立します。

  • S⊆T ⇔ T⊥⊆S⊥ ---(直交補空間 対偶の法則)

内積ベクトル空間Vの部分空間の集まりSubspace(V)は、命題論理やベキ集合のブール代数と酷似した構造を持ちます。どこまで似ていて、どこが違うかを調べるのは面白い課題です。

S⊥T のとき、S∨T を S\oplus⊥T とも書きます。S\oplus⊥T を、SとTの直交直和〈orthogonal direct sum〉といいます。S\oplus⊥T と書いたときは、S⊥Tを前提にしているので、S∧T = O （Oはゼロ空間{0}）です。直交直和の命題論理における類似物は、排他的命題の連言です。

通常の直和 S\oplusT は外部直和であり、S\oplusT ⊆ V とはいえません。それに対して直交直和 S\oplus⊥TはS∨Tのこと（ただし、S⊥T）なので S\oplus⊥T ⊆ V です。とはいえ、外部直和 S\oplusT に、S⊥Tとなるような内積を入れることが出来て、そうやって作った内積ベクトル空間も S\oplus⊥T と書くので、S\oplus⊥T ⊆ V かどうかは定義によりけりですね。

論理の排中律 P∨¬P = True （PまたはPでない は いつだって真）に相当する法則は次のように書けます。

  • S\oplus⊥S⊥ = V ---(直交補空間 排中律)

直交直和記号\oplus⊥に、S⊥S⊥の意味を込めているわけですが、\oplus⊥を使わずに2つの命題に分けたほうが分かりやすいかも知れません。

  1. S∧S⊥ = O = {0} ---(部分空間と直交補空間の排他性)
  2. S∨S⊥ = V ---(直交補空間 排中律 ジョイン版)

直交補空間の排中律から、一意直交分解が可能となります。

  • 任意の v∈V は、s∈S と t∈S⊥ により、v = s + t と一意的に分解できる。 ---(直交分解の原理)

ホッジの分解定理（ラプラシアンなしバージョン）

U, V, Wが有限次元の内積ベクトル空間だとして、F:U→V, G:V→W を線形写像とします。FとGは次の条件を満たすとします。

  • F;G = 0 :U→W ---(複体条件)

等式右辺の0はゼロ写像のことです。F;G = 0 と Im(F) ⊆ Ker(G) は同じことです。

F, Gと共にF†, G†も考えます。これからの登場人物である空間・写像は次のようです（3つの空間と4つの写像）。

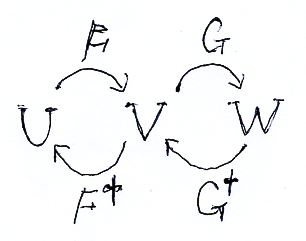
F;G = 0 を満たす (U, V, W, F, F†, G†, G) は、共変／反変を一緒にした代数的複体（前回の第2節と第9節を参照）の一部を切り取ったものです。なので、このような構造をミニ複体〈mini-complex〉と呼ぶことにします*5。ここから先、特別に断らなければ、このミニ複体 (U, V, W, F, F†, G†, G) に関する命題を扱います。

[追記]前回・今回で話題にしている「オモチャ」とは何なのか？ と聞かれれば、それはズバリ、ミニ複体です。ミニ複体は、有限次元内積空間の圏のなかで定義できる比較的簡単な構造です。ミニ複体に対して、ド・ラーム・コホモロジー（単一のベクトル空間）とラプラシアンが定義できます。そしてホッジ分解が成立します。背景はともかくとして、ミニ複体の議論には有限次元線形代数の概念しか使わないので、いじりやすいという意味で「オモチャ」と呼んでいいと思います。[/追記]

まず、次の補題を確認します。これは、F;G = 0 を使ってないので、随伴線形写像に関する一般的な事実です。

  • Im(G†) = Ker(G)⊥ ---(Im-Ker随伴性 1)
  • Im(F)⊥ = Ker(F†) ---(Im-Ker随伴性 2)

この2つは実質的に同じ命題なので、1番目だけ示します。

ターゲット命題： Im(G†) = Ker(G)⊥ ---(Im-Ker随伴性 1)

Im(G†) ⊆ Ker(G)⊥ と
Ker(G)⊥ ⊆ Im(G†) を示せばよい。

Im(G†) ⊆ Ker(G)⊥ を示す。

  v∈Im(G†) と仮定する。
$?(Imの定義)より
  適当な w∈W を使って v = G†(w)と書ける。

  u∈Ker(G)と仮定する。
u と v = G†(w) の内積を計算する。
     (u|v)
  =  (u|G†(w))
// $(随伴線形写像の基本性質)から
  = (G(u)|w)
// 仮定 u∈Ker(G) より G(u) = 0 だから
  = (0|w)
// $?(内積の双線形性)より
  = 0
よって、
  (u|v) = 0
u∈Ker(G)と v∈Im(G†) は任意だったから
  ∀u∈Ker(G), v∈Im(G†).(u|v) = 0
つまり、
  Im(G†)⊥Ker(G)
$(直交の言い換え)から
  Im(G†) ⊆ Ker(G)⊥
が示せた。

Ker(G)⊥ ⊆ Im(G†) を示す。

$(直交補空間 対偶の法則)から、Im(G†)⊥ ⊆ Ker(G) を示せばよい。

Im(G†)⊥ ⊆ Ker(G) を示す。

  u∈Im(G†)⊥ と仮定する。
  v∈Im(G†) と仮定する。
$?(Imの定義)より
  適当な w∈W を使って v = G†(w)と書ける。
u と v = G†(w) の内積は0だから
  (u|G†(w)) = 0
$(随伴線形写像の基本性質)から
  (Gu|w) = 0
vは任意だったからwも任意となり、$(内積の非退化性)により
  Gu = 0
つまり
  u∈Ker(G)
以上により
  u∈Im(G†)⊥ ⇒ u∈Ker(G)
uは任意だったから
  ∀u.(u∈Im(G†)⊥ ⇒ u∈Ker(G))
つまり
  Im(G†)⊥ ⊆ Ker(G)
が示せた。

Fの像Im(F)とG†の像Im(G†)は、いずれもVの部分空間です。この2つの部分空間は直交します。

  • Im(F) ⊥ Im(G†) --(コバンダリと随伴コバンダリの直交性)
ターゲット命題： Im(F) ⊥ Im(G†)

  v∈Im(F), v'∈Im(G†) と仮定する。
$?(Imの定義)より
  適当な u∈U を使って v = F(u)と書ける。
  適当な w∈W を使って v' = G†(w)と書ける。
v = F(u) と v' = G†(w) の内積を計算する。
    (v|v')
  = (F(u)|G†(w))
// $(随伴線形写像の基本性質)から
  = (G(F(u))|w)
// $(複体条件)から G(F(u)) = 0 だから
  = (0|w)
// $?(内積の双線形性)から
  = 0
よって
  (v|v') = 0
v, v'は任意だったから
  ∀v∈Im(F), v'∈Im(G†).(v|v') = 0
$(空間の直交の定義)より
  Im(F) ⊥ Im(G†) 。

さて、いよいよ今回のハイライト、ホッジの分解定理〈the Hodge decomposition theorem〉です。定理の主張は、ミニ複体において「Vに直交直和分解が作れるよ」と言っているだけですが、その意味は前回や第7節を参照してください。

  • X = Ker(F†)∧Ker(G) とすると、V = Im(F)\oplus⊥Im(G†)\oplus⊥X ---(ホッジ分解)
ターゲット命題： V = Im(F)\oplus⊥Im(G†)\oplus⊥X 

(Im(F)∨Im(G†))⊥を計算する。
    (Im(F)∨Im(G†))⊥
// $(直交補空間 ド・モルガンの法則 1)により
  = Im(F)⊥∧Im(G†)⊥
// $(Im-Ker随伴性 2: Im(F)⊥ = Ker(F†) )と$(Im-Ker随伴性 1: Im(G†)⊥ = Ker(G) )により
  = Ker(F†)∧Ker(G)
よって、
(Im(F)∨Im(G†))⊥ = Ker(F†)∧Ker(G) ---(1)

$(直交補空間 排中律)から
  V = (Im(F)∨Im(G†))\oplus⊥(Im(F)∨Im(G†))⊥
$(1)から
  V = (Im(F)∨Im(G†))\oplus⊥(Ker(F†)∧Ker(G))
X = Ker(F†)∧Ker(G) としていたので
  V = (Im(F)∨Im(G†))\oplus⊥X
$(コバンダリと随伴コバンダリの直交性)から Im(F)∨Im(G†) = Im(F)\oplus⊥Im(G†) なので
  V = (Im(F)\oplus⊥Im(G†))\oplus⊥X

ラプラシアンとホッジ分解

前節と同じ状況設定 -- つまり、ミニ複体 (U, V, W, F, F†, G†, G) があるとして、線形写像 L:V→V を次のように定義します。

  • L := G;G† + F†;F = G†\circG + F\circF† = G†G + FF† ---(ラプラシアンの定義)

この線形写像Lは、（ミニ複体の）ラプラシアン〈Laplacian〉と呼びます。この言葉の由来は前回と第7節で触れています。

ラプラシアンLに対して次が成立します。

  • Ker(L) = Ker(F†)∧Ker(G) ---(調和コチェーンの特徴付け)

これからこの命題$(調和コチェーンの特徴付け)を示します。まずは補題からです。

  • Ker(G;G†) = Ker(G) ---(随伴ラウンドトリップの核 1)
  • Ker(F†;F) = Ker(F†) ---(随伴ラウンドトリップの核 2)

この2つは実質的に同じ命題なので、1番目だけ示します。

ターゲット命題： Ker(G;G†) = Ker(G) ---(随伴ラウンドトリップの核 1) 

Ker(G;G†) ⊆ Ker(G) と
Ker(G) ⊆ Ker(G;G†) を示せばよい。

Ker(G;G†) ⊆ Ker(G) を示す。

  v∈Ker(G;G†) と仮定する。
つまり
  (G;G†)v = (G†\circG)v = G†(G(v)) = 0
v∈V と G†(G(v)) との内積を取ると
  (v|G†(G(v))) = (v|0) = 0
$(随伴線形写像の基本性質)より (v|G†(G(v))) = (G(v)|G(v)) だから
  (G(v)|G(v)) =  0
$(非自明ヌルベクトルの非存在)より
  G(v) = 0
つまり
  v∈Ker(G)
以上より
  v∈Ker(G;G†) ⇒ v∈Ker(G)
vは任意だったから
  ∀v.(v∈Ker(G;G†) ⇒ v∈Ker(G))
つまり
  Ker(G;G†) ⊆ Ker(G)
が示せた。

Ker(G) ⊆ Ker(G;G†) を示す。

  v∈Ker(G) と仮定する。
(G;G†)v を計算する。
    (G;G†)v
  = (G†\circG)v
  = G†(G(v))
// 仮定より G(v) = 0 なので
  = G†(0)
  = 0
よって
  (G;G†)v = 0
つまり
  v∈Ker(G;G†)
以上より、
  v∈Ker(G) ⇒ v∈Ker(G;G†)
vは任意だったから
  ∀v.(v∈Ker(G) ⇒ v∈Ker(G;G†))
つまり、
  Ker(G) ⊆ Ker(G;G†)
が示せた。

さて、$(調和コチェーンの特徴付け: Ker(L) = Ker(F†)∧Ker(G) )を示しましょう。$(複体条件: F;G = 0 （G\circF = 0）)があるので、Ker(F†)∧Ker(G) ⊆ Ker(L) は簡単です。逆向きの包含 Ker(L) ⊆ Ker(F†)∧Ker(G) だけを示します。

ターゲット命題： Ker(L) ⊆ Ker(F†)∧Ker(G) 

Ker(L) ⊆ Ker(G) と
Ker(L) ⊆ Ker(F†) を示せばよい。

Ker(L) ⊆ Ker(G) を示す。

  v∈Ker(L) と仮定する。
つまり
  Lv = 0
$(ラプラシアンの定義)より
  Lv = (G†G + FF†)v = 0
つまり
  G†Gv + FF†v = 0 ---(1)

$(1)の両辺にGを作用させると
  GG†Gv + GFF†v = 0
$(複体条件)より GF = 0 なので、
  GG†Gv = 0
つまり
  G†G(v)∈Ker(G) ---(2)

一方で、
  G†G(v)∈Im(G†)
$(Im-Ker随伴性 1)より Im(G†) = Ker(G)⊥ なので、
  G†G(v)∈Ker(G)⊥ ---(3)
$(2), $(3)より
  G†G(v)∈(Ker(G)∧Ker(G)⊥) ---(4)
$(直交補空間は直交), $(直交する空間の共通部分) より
  Ker(G)∧Ker(G)⊥ = {0} ---(5)
$(4), $(5)より
  G†G(v) = 0
つまり
  v∈Ker(G†G)
$(随伴ラウンドトリップの核)より Ker(G†G) = Ker(G) なので、
  v∈Ker(G)
以上より
  v∈Ker(L) ⇒ v∈Ker(G)
vは任意だったから
  ∀v.(v∈Ker(L) ⇒ v∈Ker(G))
つまり
  Ker(L) ⊆ Ker(G)
が示せた。

Ker(L) ⊆ Ker(F†) を示す。

$(1)の両辺にF†を作用させると
  F†G†G(v) + F†FF†(v) = 0 ---(6)
$(複体条件)より GF = 0 なので、
  F†G† = (GF)† = 0† = 0 ---(7)
$(6), $(7)より
  F†FF†(v) = 0
つまり
  FF†(v) ∈Ker(F†)
$(Im-ker随伴性 2)より Im(F)⊥ = Ker(F†) なので、
  FF†(v)∈Im(F)⊥ ---(8)

一方で、
  FF†(v)∈Im(F) ---(9)
$(8), $(9)より
  FF†(v)∈Im(F)⊥∧Im(F)
$(直交補空間は直交), $(直交する空間の共通部分) より
  FF†(v) = 0
つまり
  v∈Ker(FF†)
$(随伴ラウンドトリップの核 2)より
  v∈Ker(F†)
以上より
  v∈Ker(L) ⇒ v∈Ker(F†)
vは任意だったから
  ∀v.(v∈Ker(L) ⇒ v∈Ker(F†))
つまり
  Ker(L) ⊆ Ker(F†)
が示せた。

前節の$(ホッジ分解)により、V = Im(F)\oplus⊥Im(G†)\oplus⊥X と直交直和分解できるわけですが、Xは Ker(F†)∧Ker(G) でした。この節の$(調和コチェーンの特徴付け)によれば、Ker(L) = Ker(F†)∧Ker(G) なので、ホッジ分解を次の形に書き直すことができます。

  • V = Im(F)\oplus⊥Im(G†)\oplus⊥Ker(L) ---(ホッジ分解 ラプラシアン版)

ラプラシアンの核空間Ker(L)とは、調和形式／調和コチェーンの空間です（前回、第7節を参照）。

ド・ラーム・コホモロジー空間

引き続き、ミニ複体 (U, V, W, F, F†, G†, G) がある状況で話をします。

$(複体条件: F;G = 0 )から Im(F) ⊆ Ker(G) が言えるので、商ベクトル空間 Ker(G)/Im(F) を作ることができます。この商ベクトル空間 Ker(G)/Im(F) を、ミニ複体のド・ラーム・コホモロジー空間〈de Rham cohomology space〉と呼びます。この言葉の由来も前回と第7節で触れています。

ド・ラーム・コホモロジー空間 Ker(G)/Im(F) は、ミニ複体から抽象的に定義されるベクトル空間で、Vの部分空間ではありません。しかし、Vの部分空間とみなすことができます。なぜなら、次の同型があるからです。

  • Ker(G)/Im(F) \stackrel{\sim}{=} Ker(L) ---(ド・ラーム・コホモロジーの調和コチェーン表現 1)

ここで、Lは前節の$(ラプラシアンの定義)で定義したラプラシアンです。また前節で、$(調和コチェーンの特徴付け: Ker(L) = Ker(F†)∧Ker(G) )を示しているので、次の形でも同じです。

  • Ker(G)/Im(F) \stackrel{\sim}{=} Ker(F†)∧Ker(G) ---(ド・ラーム・コホモロジーの調和コチェーン表現 2)

この$(ド・ラーム・コホモロジーの調和コチェーン表現 2)をこれから示すことにします。

まず、内積空間の一般論を少しします。S, Tは内積空間Vの部分空間で、S ⊆ T ⊆ V だとします。S⊥は、V内でのSの直交補空間です。それに対して、(S⊥ in T) は、TのなかでのSの直交補空間を表すとします。典型例を図示すれば次のようになります。

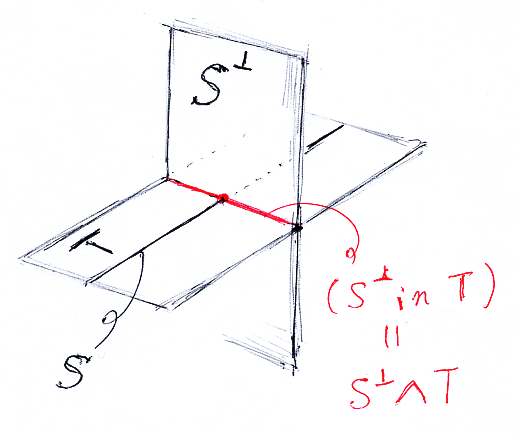
この状況で次が成立します。

  • (S⊥ in T) = S⊥∧T ---(相対直交補空間と直交補空間のミート)

これは、u∈(S⊥ in T) と u∈S⊥∧T を論理的に書いてみると、どちらも次のようになることから分かります。

  • (任意の s∈S に対して (s|u) = 0) かつ u∈T

次に、やはり S ⊆ T ⊆ V の状況で商空間と直交補空間の関係を考えます。次が成立します。

  • T/S \stackrel{\sim}{=} S⊥∧T ---(商空間と直交補空間)
ターゲット命題： T/S \stackrel{\sim}{=} S⊥∧T  ---(商空間と直交補空間)

線形代数の一般論から、$?(商空間T/Sは、TにおけるSの補空間と同型)。
これより
  T/S \stackrel{\sim}{=} (S⊥ in T)
$(相対直交補空間と直交補空間のミート)より
  (S⊥ in T) = S⊥∧T
したがって
  T/S \stackrel{\sim}{=} S⊥∧T

$(商空間と直交補空間)を、Im(F) ⊆ Ker(G) ⊆V に対して適用します。すると次が言えます。

  • Ker(G)/Im(F) \stackrel{\sim}{=} Im(F)⊥∧Ker(G)

$(Im-Ker随伴性 1)から、Im(F)⊥ = Ker(F†) なので、

  • Ker(G)/Im(F) \stackrel{\sim}{=} Ker(F†)∧Ker(G)

これは、$(ド・ラーム・コホモロジーの調和コチェーン表現 2)そのものです。

以上より、Ker(G)/Im(F) \stackrel{\sim}{=} Ker(F†)∧Ker(G) が得られました。左辺はド・ラーム・コホモロジー空間、右辺はラプラシアンの核空間だったので、ミニ複体において：

  • ド・ラーム・コホモロジー空間 \stackrel{\sim}{=} ラプラシアンの核空間

多様体から線形代数へ

前回の記事と今回の記事の大きな流れとしては、「多様体 → 有限離散近似 → 有限次元線形代数」という翻訳をしています。したがって、有限次元線形代数の範囲内だけで証明された定理に、その起源として、多様体上の幾何・解析的な事実が対応しています。

「多様体 → 有限離散近似」という翻訳は、次のような対応をもとにしています。

多様体 有限離散近似
多様体 M 幾何複体 K
特異チェーンの空間 Ck(M) 組み合わせチェーンの空間 Ck(K)
微分形式の空間 Ωk(M) 組み合わせコチェーンの空間 Ωk(K)
境界作用素 ∂k:Ck(M)→Ck-1(M) 境界作用素 Bk:Ck(K)→Ck-1(K)
外微分作用素 dk:Ωk(M)→Ωk+1(M) 余境界作用素 Dk:Ωk(K)→Ωk+1(K)
ベルトラミ作用素 δk:Ωk(M)→Ωk-1(M) ベルトラミ作用素 Ak:Ωk(K)→Ωk-1(K)
ラプラシアン Δk:Ωk(M)→Ωk(M) ラプラシアン Lk:Ωk(K)→Ωk(K)
調和形式の空間 Θk(M) = Ker(Δk) 調和コチェーンの空間 Θk(K) = Ker(Lk)

幾つかの注意事項を述べます。

「多様体Mを、幾何複体Kで有限離散近似する」ことから話が出発しているわけですが、どんな多様体が有限離散近似可能なのか？ そもそも、それは近似になっているのか？ といった問題はほとんど議論してません。これは難しい問題です。が、個別事例においては「頑張って近似しよう」という態度でもいいのかな、と思います。

Ck(-)とΩk(-)は互いに双対空間となっています。この双対性は、ペアリング〈pairing | evaluation map | 評価射〉 <-|->:Ck(-)×Ωk(-)→R により与えるのがスッキリすると思います。多様体の場合は、微分形式の特異コチェーンに沿った積分がペアリングであり、有限離散近似では、チェーン空間×コチェーン空間上の非退化双線形形式がペアリングになります。

多様体のド・ラーム・コホモロジーは、外微分作用素さえ作れば定義できます。しかし、ホッジ分解の定式化には、Ωk(M)の内積が必要です。内積の構成はけっこう大変です。リーマン計量、外積代数、ホッジ・スター演算子、体積形式による積分などの道具が必要になります。それに対して有限離散近似では、いきなり「Ωk(K)に内積があるとしましょう」でした(苦笑)。個別事例においては、“自然な内積”が見つかりそうだからです。ただ、“正しく近似する”立場からは、有限離散近似でも系統的に内積を構成する手順が必要でしょう。

ベルトラミ作用素〈Beltrami operator〉とは、外微分作用素／余境界作用素の随伴線形写像のことです*6。余微分作用素〈codifferential operator〉と呼ばれることが多いのですが、用語法が混乱する（後述）ので、「ベルトラミ作用素」と呼ぶことにします*7。ベルトラミ作用素は、Ωk(-)→Ωk-1(-) と次数を下げるので、（δk, Akのように）添字は下にしたほうが良かったかも知れませんが、添字ルールはほころびを避けられないので気にしないことにしましょう。

多様体のΩk(M)の要素をk次微分形式／k-形式と呼ぶのですが、外微分作用素／ベルトラミ作用素との関連で、以下のような分類がされています。

呼び名 英語 意味
k次閉形式 closed form of deg. k Ker(dk)の要素
k次完全形式 exact form of deg. k Im(dk-1)の要素
k次余閉形式 coclosed form of deg. k Ker(δk)の要素
k次余完全形式 coexact form of deg. k Im(δk-1)の要素

ウーム、覚えられない。双対を意味する「コ」と「随伴」を形容詞に使ったほうが幾分か系統的でマシだと思います。

伝統的呼び名 マシな呼び名 意味
k次形式 k-コチェーン Ωk(M)の要素
k次閉形式 k-コサイクル Ker(dk)の要素
k次完全形式 k-コバンダリ Im(dk-1)の要素
k次余閉形式 k-随伴コサイクル Ker(δk)の要素
k次余完全形式 k-随伴コバンダリ Im(δk-1)の要素

さて、多様体からその有限離散近似に移った後で、特定のkに注目して、3つの空間 Ωk-1(K), Ωk(K), Ωk+1(K) とそのあいだの余境界作用素／ベルトラミ作用素 Dk-1, Dk, Ak+1, Ak を抜き出します。

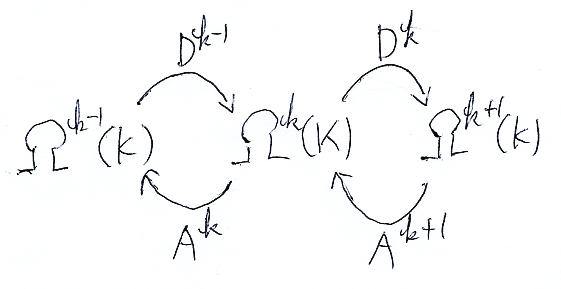
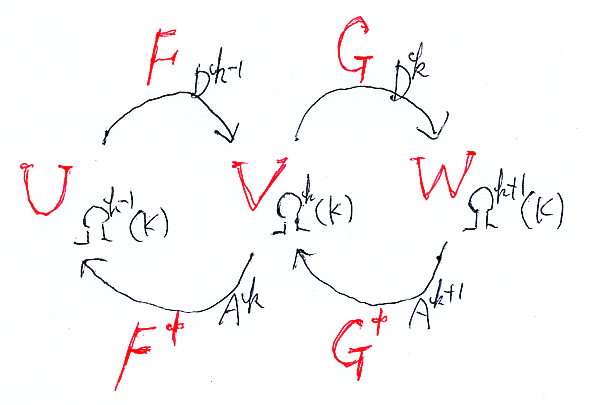
そして、次のような名前の付け替えをします。

有限離散近似 有限次元線形代数
Ωk-1(K) U
Ωk(K) V
Ωk+1(K) W
Dk-1:Ωk-1(K)→Ωk(K) F:U→V
Ak:Ωk(K)→Ωk-1(K) F†:V→U
Dk:Ωk(K)→Ωk+1(K) G:V→W
Ak+1:Ωk+1(K)→Ωk(K) G†:W→V

この表の右の欄 U, V, W, F, F†, G, G† によりミニ複体を構成しました。ミニ複体に対する有限次元線形代数の議論（いわばミニ・ホモロジー代数）を展開したのが、今回の第2節から第6節です。

ミニ複体のラプラシアンの定義 L := G†G + FF† :V→V は、適当なkにおいて、Lk := Ak+1Dk + Dk-1Ak となり、これは多様体上の Δk := δk+1dk + dk-1δk に対応します。そして、k次の離散ラプラシアンLkの核空間Ker(Lk)は、k次の調和形式の空間 Θk(M) = {α∈Ωk | Δk(α) = 0} に対応します。

有限次元線形代数の言葉で語られたホッジの分解定理を、多様体上に戻して解釈すれば：

  • k次微分形式の空間は、“コバンダリの空間”と“随伴コバンダリの空間”と“調和形式の空間”に直交直和分解される。

同様に、ド・ラーム・コホモロジーに関する定理は：

  • 微分形式のド・ラーム複体から構成されたド・ラーム・コホモロジーのk次の空間は、k次調和形式の空間と同型である。

もちろん、多様体上での理論は、有限次元線形代数で済むオモチャとは随分と違います。微積分の知識（ストークスの定理やポアンカレの補題）や、ド・ラーム・コホモロジー以外のホモロジー論（特異ホモロジーとチェック・コホモロジー）も必要になります。しかしそれでも、代数的な大枠は、オモチャと共通する部分があります。

おわりに

前回の記事と今回の記事でやってみたことは、なめらかな関数のグラフを折れ線で近似して、いくつかの数値データを取り出して、それを加減乗除だけの算数で計算したようなものです。算数の計算だけを見れば、それほど難しいことはなく、むしろ味気ないかも知れません。しかし、そのような算数計算も、もとの関数のグラフにおいて解釈すればなにがしかの意味はあるのです。

この2回の記事は、目で見えて手で触れるオモチャの提供が目的なので、端折った雑な議論が多かったです。連続的な対象物・現象の有限離散近似を真面目に考えるのは、もはやオモチャや遊びの域を越えて、シリアスなチャレンジとなります。体力・気力に満ちたアナタにお任せします。

*1:一般化された内積では、v ≠ 0 で (v|v)= 0 であるベクトルの存在を認めていて、それを（非自明な）ヌルベクトルと呼びます。

*2:すぐ後で定義されるカリー化内積Φの核がゼロ空間であることを意味します。これにより、カリー化内積Φは単射です。「(v|v) = 0 ならば v = 0」のことを非退化性と呼ぶことも多いです。

*3:Vの枠を、数ベクトル空間RnからVへの線形同型写像 a:Rn→V だと定義すると何かと都合がいいです。正規直交枠は、Rnの標準内積を保存する内積同型写像として定義できます。

*4:Vの内積は V×V→R という関数なので、カリー化すると V→Lin(V, R) となります。ここで、Lin(V, R)はVからRへの線形写像の空間。Lin(V, R) = V* なので、内積のカリー化は V→V* という線形写像です。

*5:共変／反変を一緒にまとめた代数的複体を双複体〈bicomplex〉とでも呼んで、ミニ双複体とか言うのが正確でしょう。しかし、「複体」という言葉は反変／共変の方向を気にしないで曖昧に使ったりするので、片方向か双方向かが曖昧でも責められはしないでしょう。

*6:有限離散版のベルトラミ作用素がAkとなっているのに大した理由はありません： Bだと境界作用素とかぶるので、余境界作用素DのAdjointだからAとしただけ。

*7:余微分作用素をベルトラミ作用素と呼んでいる前例は記憶にあるのですが、今、見つからない。