このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

確率的圏における期待値と雑音

雑記／備忘

確率的圏〈stochastic category | 確率圏〉の暫定的定義については「確率的圏、存在命題とスコーレム・コンビネータ // 確率的圏」で述べました。確率的圏は、事実上ジリィモナドのクライスリ圏です。こう定義してみても、期待値の概念は現れません。期待値を計算することは多いので、圏論的確率論で期待値が扱えないのは困ります。

とりあえず、特定の目的を想定して、そこで使えそうな期待値概念を定義しましょう。特定の目的とは、「雑音が乗る／真の値を推測する」という言葉にハッキリした意味を与えることです。

[追記]この記事は、使っている記法の関係で読みにくいかも知れません。読みにくさの原因や対処については：

[/追記]

内容：

雑音〈誤差〉が混じった関数

現象そのものは確率的ではなく（つまり決定的であり）、現象を我々が観測するときに誤差が混じってしまうのだ、と考えましょう。これは、世界観や信念を述べているわけではありません。単に、問題を考える上での前提を述べているだけです。

f:X → Y が、現象を記述する関数〈写像〉とします。x∈X を特定すれば、値 f(x)∈Y も一意に確定します。ところが、観測手段／装置のせいで、f(x) が揺らいでしまうのです。f(x) からズレた値が（観測手段／観測装置により）報告されることがあります。このズレは確率的現象として見れば法則的です。つまり、f(x) からの揺らぎ〈観測誤差〉の確率分布が与えられています。そして、この確率分布の“期待値”を取れば“真の値” f(x) が得られると仮定します。

上記のごとき仮定・想定は珍しくはないし、それを受け入れている場合も多いでしょう。この記事では、この仮定・想定で話をします。

「誤差」と「雑音」は同義語として使います。個人的な好みとして「誤差」より「雑音」が好きなので、「雑音」を主に使います。本来決定的である現象が揺らいでしまう（滲んでしまう）のは雑音のせいです。

「期待値」「平均値」「重心」も同義語です（人によっては区別するかも知れませんが）。一番よく使われてそうな「期待値」を主に使います。期待値を使って雑音が乗る前の値を推測できます。あるいは、期待値で除去できる程度の（タチの良い）雑音しか考えません。

記号の約束

Measをすべての可測空間と可測写像からなる圏として、MはMeasの部分圏とします。ジリィモナド、またはジリィモナドの変種がM上に定義できるとします。つまり、自己関手 G:M → M があり、自然変換 μ::G*G ⇒ G:M → M, η::IdM ⇒ G:M → M と共に、モナド (G, μ, η) を形成しています。可測空間 X∈|M| に対する G(X) は、X上の確率分布〈確率測度〉全体の集合に適切な可測構造（「拡張スタイルのジリィモナド // 確率測度達の可測空間」参照）を入れたものです。

Sは、M上のモナド G = (G, μ, η) のクライスリ圏だと約束します。

  • S := Kl(M, G) （Klはクライスリ圏を構成するオペレータ）

Sの射 F:X → Y は、Mのなかで見れば F:X → G(Y) という形の射です。

  • F:X → Y in S ⇔ F:X → G(Y) in M

SとMのあいだを頻繁に往復するので、上記の関係は常に意識しておいてください。

Sの射（クライスリ射）はマルコフ核で、Sの結合（クライスリ結合）はチャップマン／コルモゴロフ結合です（「マルコフ核： 確率計算のモダンな体系」参照）。Sの射と結合に対して、特別な矢印記号／特別な結合記号を使うことはしません（だって、めんどくさいんだもん）、だいぶ紛らわしいかも知れないので十分注意してください（[追記]「モナド、クライスリ圏、随伴 の落ち穂拾い」参照[/追記]）。次の約束はだいたい守ります。

  • Sの射（マルコフ核）は大文字で表す。
  • Mの射（可測写像）は小文字で表す。

デルタ関手（「マルコフ核： 確率計算のモダンな体系 // デルタ関手」参照）δ:M → S で、MはSに埋め込めます。δ(f) を単にfと書くことがあります。

射の結合〈composition〉記号は、図式順〈diagrammatic order〉のセミコロンを主に使います。

期待値代数

期待値、平均値、（アフィン空間における）重心はだいたい同じものです。n個の実数 x_1, \cdots, x_n があったとき、それらの平均値は：

  • \frac{1}{n}\sum_{i=1}^n x_i = \sum_{i=1}^n \frac{1}{n}x_i

x_1, \cdots, x_n を平等に扱うのではなくて重み \lambda_1, \cdots, \lambda_n を付けて平均すれば：

  • \sum_{i=1}^n \lambda_i x_i \:\:\:(\lambda_i > 0,\,\sum_{i=1}^n \lambda_i = 1)

この“平均値を求める計算”を、形式的凸結合〈formal convex combination〉 \sum_{i=1}^n \lambda_i \langle x_i\rangle から実際の値を求めたのだ、とみなしましょう。今出てきた \langle x_i\rangle は単なる記号とみなした x_i です。実数から作られた形式的凸結合の全体を Convex(R) とすると、平均値〈重心〉である実数値を求める写像は：

  • e:Convex(R) → R

'e'はevalからです。

ところで、形式的凸結合の集合を作る操作 Convex(-) は（適切な乗法μ、単位ηと共に）モナドになります。モナドConvexと上記の平均値〈重心〉を求める写像eのあいだには、次の関係があります。

  1. \eta_{\bf R};e = \mathrm{id}_{\bf R} \:: {\bf R} \to {\bf R} （eはモナド単位ηと整合的）
  2. Convex(e);e = \mu_{\bf R};e \:: G(G({\bf R})) \to {\bf R} （eはモナド乗法μと整合的）

一番目の等式は、単一の実数の平均値はその実数であること、二番目の等式は、入れ子になった形式的凸結合の平均値を求める二つの方法が同じ値を与えることを主張しています。もう少し詳しい説明は次の記事に書いてあります。

今述べたことを、モナド理論の言葉で述べれば：

  • (R, e) は、集合圏上のモナドConvexのアイレンベルク／ムーア代数になっている。

アイレンベルク／ムーア圏（アイレンベルク／ムーア代数の圏）についての入門的解説は次の記事を見てください。

  1. アイレンベルグ／ムーア圏 その1
  2. アイレンベルグ／ムーア圏 その2:リストモナドのとき
  3. アイレンベルグ／ムーア圏 その3:Maybeモナドのとき

クライスリ圏とアイレンベルク／ムーア圏との関係は次の記事をどうぞ。

さて、平均値〈重心〉と期待値は似たようなものなので（って、どえらく乱暴な議論）、期待値は、ジリィモナドGのアイレンベルク／ムーア代数で定義できると思っていいでしょう。可測空間Xと、e:G(X) → X in M （今度の'e'はexpectation）の組 (X, e) がジリィモナドGのアイレンベルク／ムーア代数になっているとき期待値代数〈expectation algebra〉と呼ぶことにします*1。

期待値代数 (X, e) は次の法則を満たします。

  1. \eta_X;e = \mathrm{id}_X \:: X \to X （アイレンベルク／ムーア代数の単位律）
  2. G(e);e = \mu_X;e \:: G(G(X)) \to X （アイレンベルク／ムーア代数の結合律）

雑音

我々の今の定式化では、期待値を取るメカニズムは、ジリィモナドGのアイレンベルク／ムーア代数として表現されます。ということは、ジリィモナドGのアイレンベルク／ムーア圏で話をするのが良いように思えます。おそらくそうなのでしょう。しかし、いきなりアイレンベルク／ムーア圏に舞台を移すのは戸惑いがあります。中途半端ではありますが、当面次のように扱います。

  • ジリィモナドGのクライスリ圏Sを使い続ける。Sの対象は可測空間で、射はマルコフ核である。
  • 可測空間Xに対して、写像 eX:G(X) → X が割り当てられており、(X, eX) は期待値代数である*2。

この中途半端な仮定でしばらく議論してみれば、アイレンベルク／ムーア圏の状況も見えてくるだろうと（楽観的に）考えてます。

「雑音が乗る」現象をハッキリと定義するために、まずは雑音を定義します。α:X → G(X) in M がX上の雑音〈noise〉だとは、次を満たすことです。

  • α;eX = idX in M

α:X → G(X) in M ⇔ α:X → X in S なので、X上の雑音は圏Sの自己射〈endomorphism〉です。2つの雑音 α, β:X → X in S のSでの結合（Mでの結合ではない！）は再び雑音になります。α;β in S はクライスリ結合なので、M内で見ると α;G(β);μX と書けます。これに、e:G(X) → X in M を後結合して、期待値代数の結合律を利用して計算すると、α;β in S が雑音の条件を満たすことがわかります。idX:X → X in S は、Mで考えれば ηX:X → G(X) in M で、ηX が雑音なのは期待値代数の単位律から明らかです。

X∈|S| に対して、X上の雑音の全体を Noise(X) と書くことにします。Noise(X) ⊆ S(X, X) と考えると、前段落の結果から、圏Sの結合をモノイド演算として Noise(X) はモノイドになります。これを雑音モノイド〈noise monoid〉と呼んでおきましょう。なお、雑音＝雑音モノイドの要素 は（ラテン文字大文字ではなくて）ギリシャ文字小文字で表します。

雑音の例としては、有限次元アフィン空間上のガウス雑音（ガウス分布で定義される雑音）が典型的です。

ノイジー射

「分布から拡散へ： ミシェル・ジリィを巡って」において、マルコフ核の直感的な説明として、値が滲んでしまう写像〈関数〉の絵を載せました。

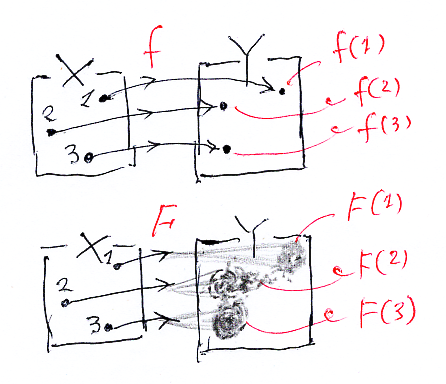
この絵では、x∈X に対する F(x) が「なぜ／どこで」滲んでしまうかは問題にしていません。

今回は、決定性写像〈シャープ射〉 f:X → Y in M が、Y側の雑音によって滲んでしまうとします。F:X → Y in S が、f:X → Y in M と雑音 β:Y → Y in S （β:Y → G(Y) in M）により F = f;β :X → G(Y) in M（Sで考えれば、F = δ(f);β :X → Y in S）と書けるときノイジー射〈noisy morphism〉と呼びましょう。ノイジー射が、「現象そのものは確率的ではなく、現象を我々が観測するときに誤差〈雑音〉が混じってしまう」ことの定式化になります。

βがY側の雑音であることから、Y上の期待値代数 (G(Y), eY) の演算 eY:G(Y) → Y in M を使えば、

  • F;eY = (f;β);eY = f;(β;eY) = f;idY = f in M

として“真の写像” f:X → Y in M が取り出せます。

雑音の前方シフト

ノイジー射は、単に滲んだ写像ではなくて、期待値を取れば“真の姿”である決定性写像〈シャープ射〉が得られるものです。2つのノイジー射を結合〈クライスリ結合 | チャップマン／コルモゴロフ結合〉したらノイジー射が得られるかどうかは分かりません。どういうセッティングなら、ノイジー射とノイジー射の結合をノイジー射として計算できるでしょうか？

この問に対して計算の枠組みだけ提示しても、実例がないとあまり意味がないのですが、実例を構成するときのヒントとしてメモしておきましょう。

ノイジー射をS内で結合すると、複数の雑音が絡まり合ってしまって、余域〈ターゲット〉側で期待値を取る単純な方法では“真の値”を推測できなくなります。シャープな部分と雑音をいつでも分離できればうまくいくのですが‥‥。雑音の発生場所を移動可能という仮定を入れてみます。

雑音 α∈Noise(X), β∈Noise(Y) とシャープ射〈決定性写像〉f:X → Y in M があって、次の等式が成立しているとします。

  • α;G(f) = f;β :X → G(Y) in M

このとき、αとβは、fに沿ったシフトペア〈shifted pair〉だと言うことにします。αを基準にした場合は、βはαの前方シフト〈forward shift〉、βを基準とした場合は、αはβの後方シフト〈backward shift〉と呼びましょう。

雑音の前方シフトが出来れば、シャープ射（複数）と雑音（複数）が絡まり合わないように管理できます。MとSのなかで前方シフトが出来るとは期待できないので、部分圏を考えます。

  • Cは、Mの広い部分圏〈wide subcategory〉
  • Nは、雑音からなるSの広い部分圏 （X ≠ Y ならば、N(X, Y) = 空）

Cの結合は関数結合、Nの結合はクライスリ結合〈マルコフ核のチャップマン／コルモゴロフ結合〉なので注意してください。

以上のセッティングで、次の命題FSHIFTを考えます。

\mathrm{FSHIFT} :\Leftrightarrow \\ \:\:\forall \alpha \in \mathcal{N}(X, X),\, f \in \mathcal{C}(X, Y) . \\ \:\:\exists \beta \in \mathcal{N}(Y, Y).\\ \:\:\:\: \alpha ; G(f) = f;\beta \:: X \to G(Y) \mbox{ in } \mathcal{M}

正確に言えば、この命題の外側に \forall X, Y \in |\mathcal{C}|. が付いています。

圏 M, S と、それらの部分圏 C, N から構成される構造において、命題FSHIFTが成立していると仮定します。命題FSHIFTは存在命題なので、そのスコーレム・コンビネータを構成できます（「確率的圏、存在命題とスコーレム・コンビネータ」参照）。FSHIFTのスコーレム・コンビネータをFShiftとします。

  • FShiftX,Y:N(X, X)×C(X, Y) → N(Y, Y) （N(X, X)⊆Noise(X), N(Y, Y)⊆Noise(Y)）

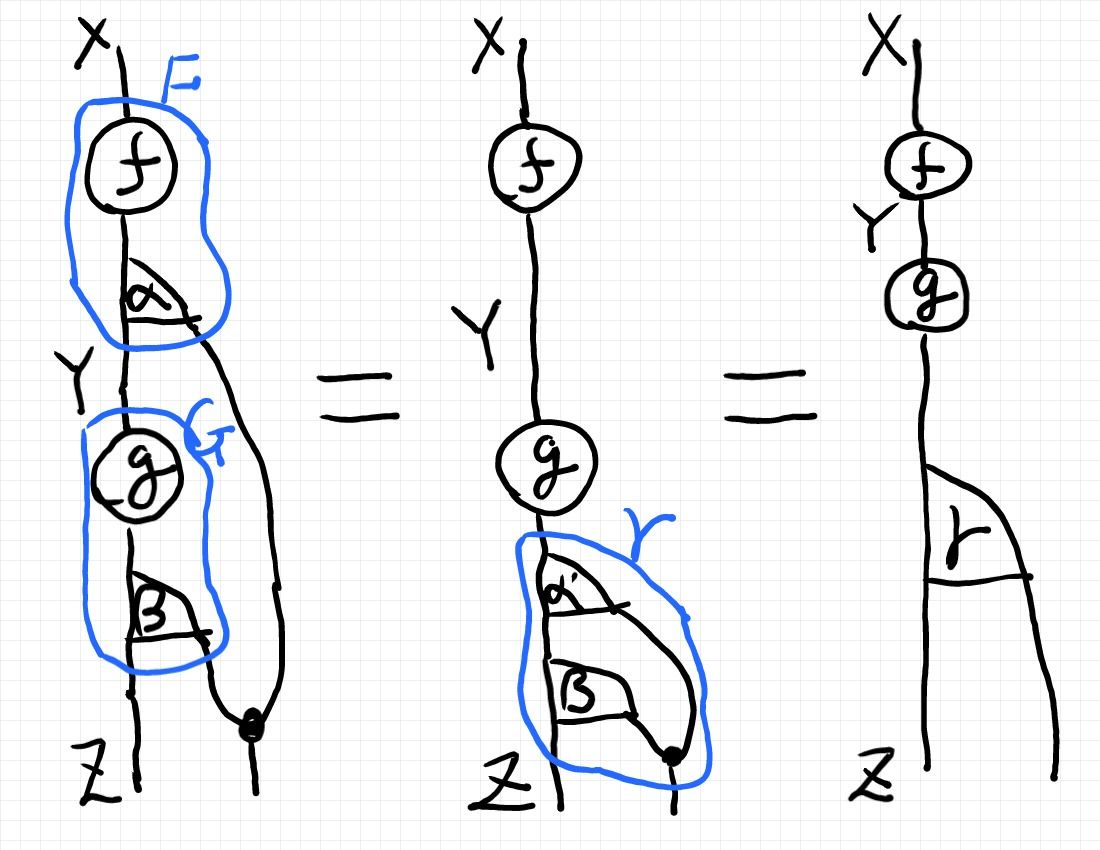
コンビネータFShiftを使えば、ノイジー射のクライスリ結合〈チャップマン／コルモゴロフ結合〉をシャープ射と雑音に分離できます。F = f;α :X → Y, G = g;β :Y → Z in S （F = f;α :X → G(Y), G = g;β :Y → G(X) in M）としましょう。ウッ、ウギャッ！ 'G'がジリィモナドとかぶった。だが、説明用の絵を描いてしまったので直さない。ここだけ、Gは射です。α, β の使い方も今までとは違ってしまいました、ゴメン。で、ともかく、次の計算ができます。

  • F;G = (f;α);(g;β) = f;(α;g);β = f;(g;α');β = (f;g);(α';β) = (f;g);γ
    where α' := FShift(α, g), γ = α';β

この計算は、Mでやっているんだか、Sでやっているんだかよく分からない計算です（[追記]「モナド、クライスリ圏、随伴 の落ち穂拾い」参照[/追記]）。間違いなく計算するには絵算を併用するといいですよ。

*3

この絵の描画方向は上から下で、縦方向 X→Y→Z のワイヤーの左側の面は自明圏、右側の面は圏Mを表します。ラベルしてないワイヤーとノードはジリィモナドの構成素です。射を自然変換に格上げして描く図法なので、ちょっと見では分かりにくいかも知れません。次の記事などで描き方を説明しています。

雑音の前方シフトの自明な例はすぐ作れますが、実用的な例は難しいかも知れません。前方シフトがあれば嬉しいですが、「前方シフトがないと何もできない」とかではないので、前方シフトが構成できなくても悲観することはないでしょう*4。

それから

前方シフトのあるなしに関わらず、前節で設定した C⊆M, N⊆S の構造は役に立ちそうです。ひとつの仮定・想定として、現象の真の姿である決定性写像達の圏Cと雑音達の圏Nを設定します。この設定で定義されるノイジー射は、余域〈ターゲット〉側で期待値を取るだけで真の姿を露呈します。とはいえ、神ならぬ我々は、雑音〈誤差〉が乗った有限個の観測データしか入手できないわけで、それから現象の真の姿を計算するにはアルゴリズム的な話が必要になります。

と、課題を述べたところでオシマイ。

*1:凸代数と呼ぶことが多いかも知れません。「二点しかない離散空間に長さ1の線分を描けるか？」に凸代数の話を書いています。

*2:単なる可測空間ではなくて期待値代数を考えるので、結局、アイレンベルク／ムーア圏の対象を扱うことになります。

*3:Web上の画像： https://sketch.io/render/sk-5a1db6675b9f6ddf8617916e1975e4aa.jpeg

*4:[追記]ノイジー射や雑音の前方シフトが重要な概念だとは思っていません。もっと良い別な概念があるだろうと思います。ノイジー射／前方シフトは、主役ではなくて脇役となるでしょう。[/追記]