確率的不確定性を伴う状況の記述や分析の手法に確率グラフィカルモデル〈probabilistic graphical model〉があります。ベイズネットワーク〈Bayesian network〉が有名です。ベイズネットワークは有向グラフを使いますが、無向グラフを使うグラフィカルモデルもあります(マルコフ確率場)。
ベイズネットワークに関しては、「フォングの“因果セオリー”の理論」で紹介したフォング論文で圏論的定式化がされています。ベイズネットワークの有向グラフは圏のストリング図と解釈できます。フォングはクセのあるストリング図を使っていますが、独特なストリング図を使った理由は「因果セオリー論の語法・記法・図法(修正案付き)」で説明しました。
無向グラフを使うグラフィカルモデルの圏論的定式化はどうでしょうか? 無向グラフはそのままではストリング図とみなせません。向きを付ける必要があります。逆に、向きが付いているストリング図から無向グラフを得るには、向きを取り去ります。グラフに向きを付けたり取り去ったりが自由に出来るためには、背後にある圏(それがあるとして)が特別な構造を持つ必要があります。
有向ストリング図(通常のストリング図)は、どんなモノイド圏でも使える図示法*1ですが、無向ストリング図が使えるモノイド圏はホントに特殊です。“無向ストリング図を許す圏”を定義して、無向グラフィカルモデルの背後に、そんな圏がほんとに存在するのかを探ります。
内容:
グラフィカルモデルからストリング図へ
詳細は棚上げして、確率グラフィカルモデルで使う図の実例を2つ挙げます。
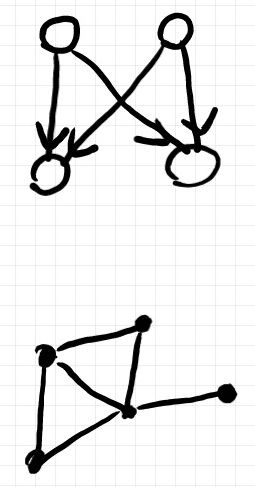
上はベイズネットワークの有向グラフで、下はマルコフ確率場の無向グラフです。頂点が白丸だったり黒丸だったりは特に意味はないです(ゆるい習慣)。無向グラフの解釈には、ハイパーグラフとかクリーク複体とか難しい話が出てくることがありますが、ストリング図に直してしまえば、ハイパーグラフ/クリーク複体なんて概念は不要です。
上の2つのグラフ(有向グラフと無向グラフ)をストリング図に描き換えると、次のようになります。
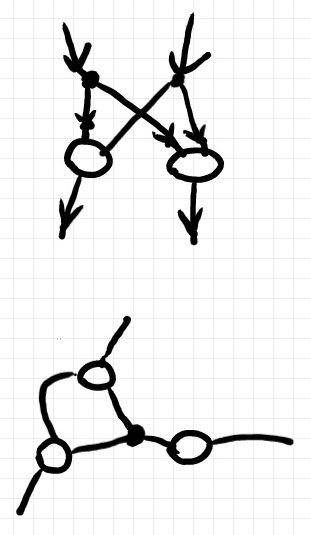
今度は、白丸と黒丸に意味があります。図をフローチャートだと思うと、白丸は処理ノードで、黒丸は分岐点・合流点を表します。もっとも、無向グラフでは“フロー”が発生しないので、処理と分岐・合流としての解釈は難しいです -- そこが今回の問題点・課題です。
有向グラフはさほど問題がないので、無向グラフに注目しましょう。“確率グラフィカルモデルで使う無向グラフ”から“無向ストリング図”に変換する手順を説明します。説明に、単体〈simplex〉という言葉が必要です。線分、三角形、四面体などを総称して単体といいます。線分=1次元単体、三角形=2次元単体、四面体=3次元単体 です。
- 無向グラフで、単体に見える所に白丸を描きます。ただし、より大きな単体の一部となっている単体(例えば、三角形の辺)には白丸を付けません。
- 頂点(黒丸、ドット)と白丸を残してもとの辺は消します。
- 単体を表す白丸と、単体の頂点である黒丸を辺で結びます。
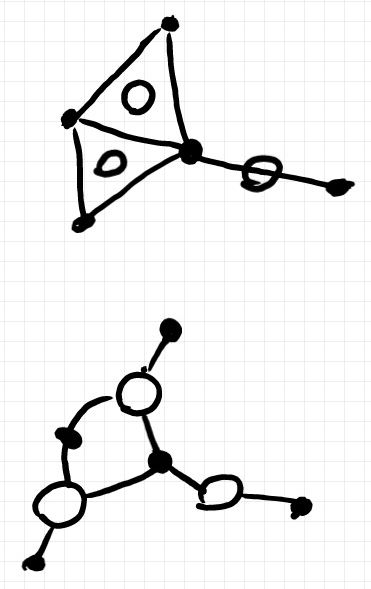
分岐・合流点ではない黒丸は消してしまってもかまいません。が、残しておいたほうが分かりやすいかも知れません。
ストリンググラフと因子グラフ
ストリング図は有向グラフだと言われますが(僕も言ってますが)、実は、ストリング図は普通の意味の有向グラフではありません。例えば次の簡単なストリング図を考えてみましょう。
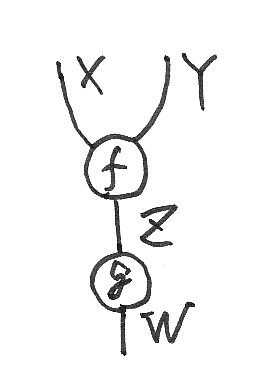
有向辺(矢印がなくても上から下の方向だと思う)は4本あります。有向グラフであれば、有向辺の両端にノード〈頂点〉があるはずです。両端にノードを持つ有向辺はZだけで、X, Y, W とラベルされている有向辺には両端が揃っていません。つまり、ストリング図は有向グラフではないのです。
ストリング図を有向グラフだとみなすためには、二種類の頂点を導入する必要があります。二種類の頂点を持つ有向グラフをストリンググラフといいます。ストリンググラフについては、次の記事を見てください。
上のストリング図をストリンググラフとして描くと:
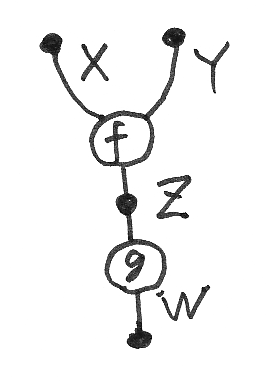
黒丸はワイヤー頂点、白丸はノード頂点と呼びます。以下、ワイヤー頂点をドット、ノード頂点を単にノードと呼びます。前節の最後に「黒丸は残しておいたほうが分かりやすいかも」と書いたのは、黒丸をドット〈ワイヤー頂点〉とみなしてストリンググラフになるからです。
前節最後のグラフには、分岐・合流の黒丸があります。ストリンググラフのドットに出入りする辺は1本か2本に限られます。3本以上の辺が集まるドットはストリンググラフでは許しません。3本以上の辺が集まるドットは別途解釈する必要がありますが、図を解釈する舞台である圏が、対角や余対角を持てば、3本以上の辺が集まるドット(分岐・合流の黒丸)に意味を与えることができます。
ストリンググラフとほとんど同じ発想の図示法に因子グラフがあります。次の記事で紹介しています。
ストリンググラフと因子グラフの対応関係は:
| ストリンググラフ | 因子グラフ |
|---|---|
| ドット〈ワイヤー頂点〉 | 変数ノード |
| ノード〈ノード頂点〉 | 関数ノード |
ストリンググラフ(有向グラフ)に分岐ドットと合流ドットを許しても、因子グラフにおいては「分岐ドット=変数値のコピー、合流ドット=足し算」として解釈できます。
しかし、ストリンググラフも因子グラフも有向グラフなので、無向ストリング図を解釈するには別な手段が必要です。
置換曲げ同値関係
有向ストリング図(通常のストリング図)のノードには、何本かのワイヤーが接合されますが、それらは入力側と出力側にキッチリと分けられます。また、入力側/出力側のワイヤー達のあいだには順序〈全順序〉が決まっています。それによって、ストリング図のノードによりモノイド圏の射、例えば f:AB → B
C が表現できます。むしろ、モノイド圏の射の表現としてノードが在ると言ったほうがいいでしょう。
ところが、無向ストリング図のノードでは:
- ワイヤーに、入力ワイヤーと出力ワイヤーの区別はない。
- 複数のワイヤーのあいだに順序は存在しない。
よって、無向ストリング図のノードを圏の射と解釈するには、次の操作が必要です。
- ワイヤーが、入力ワイヤーか出力ワイヤーかを決める。
- 入力側ワイヤーのあいだ、出力側ワイヤーのあいだに、順序〈全順序〉を与える。
入出力の別と順序の与え方は一通りとは限らないので、ひとつの無向ノードからたくさんの有向ノードが生まれるかも知れません。逆に考えると、幾つかの有向ノードが単一の無向ノードへとグループ化されます。つまり、無向ノードは、有向ノードの同値類だと言えます。
では、有向ノードの集合にどんな同値関係を入れればよいのでしょうか? ワイヤーの置換(入れ替え、交差)と、ワイヤーの折り曲げ(方向を逆転させる)で移りあえるノードは同値とすればよさそうです。この同値関係を'≡'で表すと、例えば次のような同値があります。
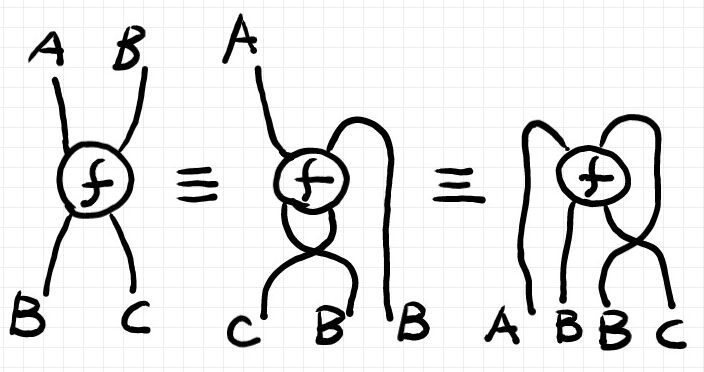
図を上から下、左から右に読むことにして、ノードをモノイド圏の射と解釈すれば、次の3つのプロファイルの射を同値としています。
- A
B → B
C
- A → C
B
B
- I → A
B
B
C
行っている図形的操作は、ワイヤーの置換〈交差〉とワイヤーを曲げていることです。この2つの操作から定義した同値関係を置換曲げ同値関係〈permutation-bending equivalence relation〉と呼ぶことにします。
自己双対コンパクト圏
ワイヤー/ノードは、圏の対象/射の図形的表示です。図形的操作であるワイヤーの置換とワイヤーの曲げは、圏の側ではどんな操作になるのでしょうか? ワイヤーの置換は、対称モノイド圏の対称〈置換〉を前結合または後結合する操作でいいでしょう。曲げもはやり、'∩'または'∪'の形をした射を前結合または後結合する操作としていいでしょう。
ところで、「'∩'または'∪'の形をした射」とは何でしょうか。コンパクト圏〈コンパクト閉圏〉の単位/余単位がその候補になります。コンパクト圏では対象の双対がありますが、退化した双対 A* = A が今の目的では便利です。A* = A が成立するコンパクト圏は、自己双対コンパクト圏〈self-dual compact category〉といいます。
自己双対コンパクト圏における単位/余単位は次のようになります。 はモノイド積、I はモノイド単位です。
対称を σA,B とすると、前節の同値な3つの射は次のように書けます。
- f :A
B → B
C
- (idA
ηB);(f
idB);(σB,C
idB) :A → C
B
B
- (ηA
ηB);(idA
f
idB);(idA
idB
σC,B) :I → A
B
B
C
けっこう複雑な式になったりしますが、もとの射に、恒等、対称、単位、余単位を組み合わせているだけです。
自己双対コンパクト圏の典型例には、関係圏Relと有限次元内積ベクトル空間〈有限次元ヒルベルト空間〉の圏FdHilbがあります。
| 関係圏Rel | 有限次元内積ベクトル空間の圏FdHilb | |
|---|---|---|
| 対象 | 集合 | 有限次元内積空間 |
| モノイド積 | 直積 | テンソル積 |
| モノイド単位 | 単元集合 | スカラー体*2 |
| 単位 | 対角集合 | 単位行列のテンソル表示 |
| 余単位 | 対角集合 | 内積の線形化 |
我々が欲しい圏は、確率グラフィカルモデルの図を解釈する場なので、関係圏でも有限次内積ベクトル空間の圏でもありません。確率的な自己双対コンパクト圏です。
ダガー構造
関係圏Relも、有限次元内積ベクトル空間の圏FdHilbも、自己双対コンパクト圏であるだけでなく、ダガー構造を持ちます。射 f:A → B に対して、そのダガー f†:B → A が定義されます。関係圏のときは関係の転置、有限次元内積ベクトル空間の圏の場合は線形写像の随伴によりダガーが与えられます。
確率的な圏もダガー構造を持てば何かと便利です。我々の希望としては、次の表の疑問符の欄を埋める圏が欲しいのです。
| 自己双対ダガーコンパクト圏 | 典型的応用 |
|---|---|
| 関係圏Rel | データベース |
| 有限次元内積ベクトル空間の圏FdHilb | 量子情報、リーマン幾何 |
| ? | 確率グラフィカルモデル |
背後に自己双対ダガーコンパクト圏があれば、無向ストリング図の解釈もできるし、コンパクト構造とダガー構造により計算も捗りそうです。
とはいえ、自己双対ダガーコンパクト圏はリッチな構造を持ち制約も強い圏です。そんな都合がいい圏が実際に在る、あるいは構成可能なのでしょうか?
見通し
確率的自己双対ダガーコンパクト圏は、おそらく構成可能です([追記]コンパクト構造は無理かも[/追記])。ベースとなるのは、確率空間(可測空間+確率測度)を対象として、確率を保存するマルコフ核を射とする圏です。この圏はちょっと“ゆるい”ので、確率に関してほとんど等しい〈almost surely equal〉という同値関係で商を作ります。
一般的な枠組みとしては、適切なマルコフ圏をDとすると、当該の圏PS(D)は次のように書けます。
- PS(D) := (1/D)/=a.s.
ここで:
- 1/D は、単位対象1に対するアンダー圏〈余スライス圏〉
- =a.s. は、各ホムセットごとに入る「ほとんど等しい」という同値関係
- (1/D)/=a.s. は、ホムセットごとの同値関係の商集合をホムセットとした圏(対象類は同じ)
PS(D) が対称モノイド圏になるのは分かりますが、自己双対ダガーコンパクト構造を構成するのは手間がかかりそうです([追記]コンパクト構造は無理かも[/追記])。が、凄く大変ってわけでもないでしょう。フリッツのテキストに書いてあったような気もします(今、確認してない)。
具合がいい確率的自己双対ダガーコンパクト圏があったとしても、確率的グラフィカルモデルと直ちに結び付くわけでもないので、架橋のメカニズムは必要です。架橋のメカニズムには、テンソル計算やシーケント計算が使えそうな気がします。たぶんだけど。