なんやかんや -- after 量子と古典の物理と幾何＠名古屋

「量子と古典の物理と幾何＠名古屋」世話人／参加者の皆様、ありがとうございました。

僕の話は、案の定、省略や言い残しがイッパイありますね。たぶんこうなるだろうと予測してたので事後資料は準備してあります。でも、事後資料を読むのは面倒でしょうから、今の時点で思い浮かぶ補足を幾つか手短に書いておきます。

内容：

1. 資料、訂正と結論
2. ネタ元とか参考文献とか
3. ハイブについて
4. フロベニウス代数とその亜種
5. ハイブの圏はなぜ3次元なのか
6. よく分からんけど

資料、訂正と結論

当日使った資料は、次のURLからアクセス可能です。

1. ハンドアウト http://www.chimaira.org/misc/story.md.html
2. チートシート http://www.chimaira.org/misc/cheatsheet.md.html

ハンドアウトの「セクション3 項目6」に間違いがありましたが、今は訂正しています。訂正後の内容を丁寧に書くと次のようです； 圏Set内の可換群（普通の可換群）を圏Rel内の可換群だと思い、関係の転置（域と余域の取り替え）により余二項演算を導入すると、二項演算と余二項演算を備えた代数系は、結合律、余結合律、フロベニウス律、星状律、余星状律を満たす。従って、三角形分割非依存なRel値関手を定義する。（各種の法則の絵はチートシートに描いてあります。）

可換群があれば、それから三角形分割非依存な関手を作れるわけです。特別な場合として、整数加法群 (Z, + , 0) から三角形分割非依存な関手を作れます。これが荷電ゾンビ（charged zombies）を使った非決定性ゾンビフロー計算の意味関手 Z:Hive→Rel です。プレーンゾンビを使っていた場合は、観測値（ドアにおける通過個体数カウント）全体が群ではないので、ハイブの内部構造＝三角形分割に影響されてしまいました。荷電＝符号を考慮したカウントならば、内部構造を漏らすことはなくなります。

[追記]

Z:Hive→Rel の具体的な記述：

• Z(1-射であるドア付き壁パネル) = Z（整数の全体）
• Z(2-射である「入るドア2, 出るドア1」の三角部屋) = (足し算:Z²→Z)
• Z(2-射である「入るドア1, 出るドア2」の三角部屋) = (余足し算:Z→Z²)
  余足し算は、足し算の転置で、入力の整数を2つの整数に加法的に分解する（非決定性）。

基本ビルディングブロックでの値が決まれば、後はハイブの部屋割りレイアウトに沿って、横結合（）と縦結合（;）の公式から計算できます。計算は双対グラフ上で行ったほうが楽です。

• Z(ab) = Z(a)Z(b) 外壁（折れ線）の横結合、Relでのは直積
• Z(AB) = Z(A)Z(B) ハイブの横結合、Relでのは関係の直積（タプルの組み換えあり）
• Z(A;B) = Z(A);Z(B) ハイブの縦結合

[/追記]

ネタ元とか参考文献とか

ほぼ10年前、「結合律の図形的解釈」とか「フロベニウス律と特殊律を満たすなら星状細分に対して不変」だとか、メモを書いているので、“このテの話題”をうっすらとは知っていたのでしょう。

• http://d.hatena.ne.jp/m-hiyama-memo/20070501

何で“このテの話題”に興味を持ったのかは記憶にありません。“このテの話題”の有名な論文というと、FHK（Fukuma, Hosono, Kawai）です。

• Title: Lattice Topological Field Theory in Two Dimensions
• Authors: M.Fukuma, S.Hosono, H.Kawai
• Pages: 29
• URL: https://arxiv.org/abs/hep-th/9212154

でも、この論文は物理的内容を物理的記法で書いてあるので、僕にはまったくサッパリ分かりません。ジョン・バエズがFHK論文を高く評価してるんですよね。"This Week's Finds in Mathematical Physics"で紹介しています。

• http://math.ucr.edu/home/baez/week16.html
• http://math.ucr.edu/home/baez/week38.html

僕は、バエズの紹介記事を読んでうっすらと分かった気になっていた、というのが10年前の状況だったんじゃないのかな、たぶん。

ラウダ／ファイファー（Aaron D. Lauda, Hendryk Pfeiffer）が、FHKのモダンな拡張を構成しています。

• Title: State sum construction of two-dimensional open-closed Topological Quantum Field Theories
• Authors: Aaron D. Lauda, Hendryk Pfeiffer
• Pages: 33
• URL: https://arxiv.org/abs/math/0602047

↑をざっと眺めれば（読まなくても）、絵算／絵等式／三角形分割などが使われているのが分かります。もっと詳しい内容はラウダの学位論文にあります。

ハイブについて

ハイブ（三角ハイブ）は、ユークリッド平面内のまっすぐな辺を持つ三角形の集まりとして導入しました。双対グラフで考えたほうが楽なので、ハイブに関する制約を双対グラフの性質として記述しました。その後なしくずしに、ハイブの圏Hiveは、制約付き有向グラフ（ストリング図）の圏Daftogと圏同値であるかのように扱っています。これはマヤカシっぽい話の展開なので、少し補足しておきます。

次元0, 1, 2に対して標準アフィン単体を次のように定義します。

• Δ⁰ = {x∈R | x = 1} = {1}
• Δ¹ = {(x₁, x₂)∈R² | x₁ + x₂ = 1 かつ x₁ ≧ 0 かつ x₂ ≧ 0}
• Δ² = {(x₁, x₂, x₃)∈R³ | x₁ + x₂ + x₃ = 1 かつ x₁ ≧ 0 かつ x₂ ≧ 0 かつ x₃ ≧ 0}

標準アフィン単体Δ^kから適当な次元のユークリッド空間R^Nへのアフィン写像 σ:Δ^k→Rⁿ で単射なものを（R^N内の）アフィン単体と呼びましょう。点集合だと考えたいのなら、σの像だけに注目してもかまいません。R^Nのなかでアフィン単体を素材とした複合図形をアフィン単体複体と呼ぶことにします。

最初の段階でハイブは、R²内のアフィン単体複体に辺（1次元単体）の向き（＝ドアの向き＝ゾンビの進行方向）を付けたものとして定義(?)しました。ハイブの条件は、双対グラフに関する次の性質（制約）で記述されます。

形容詞	グラフの性質	ハイブの性質
Directed	辺は向きを持つ。	ドアは一方通行。
Acyclic	サイクルを持たない。	ゾンビは永久に走り回らない。
Fluent	グラフを流路と見て、吸い込みも湧き出しも持たない。	ゾンビは閉じ込められないし、湧いてこない。
Trivalent	1つのノードに出入りする辺の総数は3本。	部屋の形は三角形、三方にドア。
Open	開放端を持つ。開放端は辺の端点だがノードとは違う。	入口ドアと出口ドアがある。

上記の条件DAFTOを満たすグラフをDAFTOG（DAFT Graph）と呼び、開放端を繋ぐ結合操作（composition）によりDAFTOGの全体は圏をなします。DAFTOGを射とする圏Daftogの対象は有限個の開放端点（絵では並んだドット）です。問題になるのは端点の個数だけなので、対象の集合は自然数全体Nだとしてもかまいません。さらに、端点のドット列とDAFTOGを横（図の描き方に依存するが）に並べる操作をモノイド積（テンソル積）として、Daftogはモノイド圏になります。

モノイド圏Daftogの幾何的実現がハイブの圏なので、ハイブの圏HiveはDaftogと同じ構造を持つよね、という筋書きですが、R²内のアフィン単体複体によりDAFTOGの幾何的実現が出来るのか？ というと、それは無理です。

アフィンである、つまり三角形の辺がまっすぐであるということが邪魔になります。Daftog側で結合可能（composable）な2つの射が、アフィンな双対ではうまく結合できないのです。次がその例です。

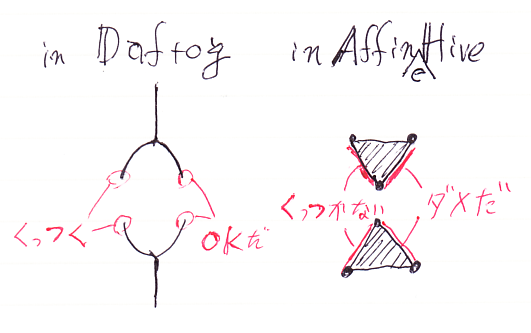
この問題を解決するには、単体の定義のなかのアフィン写像を単なる連続写像とかなめらかな（C^∞）写像に置き換えます。そうやって定義し直した単体を曲がった単体（curved simplex）と呼びましょう*1。曲がった単体から作られる複体は曲がった単体複体（curved simplicial complex）です。そして、曲がった単体複体を幾何的ベースにしたハイブは曲がった（三角）ハイブ（curved (triangular) hive）と呼びます。

曲がったハイブなら柔軟性・自由度が高いので、Daftogの結合を幾何的に実現できます。

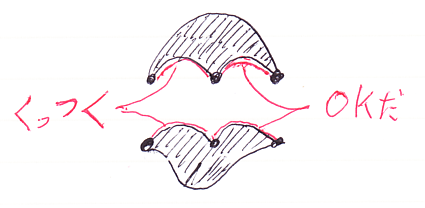
アフィンハイブの絵ばっかり描いていたのですが、ちゃんと圏の構造を持たせるには曲がったハイブまで含めてハイブの全体を考える必要があります。つまり、Hive := AffineHive ではなくて、Hive := CurvedHive と定義すべきです。

フロベニウス代数とその亜種

フロベニウス代数は、任意のモノイド圏で定義可能で、次の公理を満たす代数系 (W, m, e, c, i) です。id_Wを単にWと書きます。律子〈りつし〉は省略します。チートシートの絵等式も参照してください。

1. 結合律 (mW);m = (Wm);m
2. 左右の単位律 (eW);m = W, (We);m = W
3. 余結合律 c;(cW) = c;(Wc)
4. 左右の余単位律 c;(iW) = W, c;(Wi) = W
5. フロベニウス律 c;m = (cW);(Wm), c;m = (Wc);(mW)

三角形分割または三価（ノードに集まる辺が3本の）グラフを使う限り、単位律／余単位律を表現する手段がありません。そこで、単位律／余単位律を外したものを非単位的フロベニウス代数（non-unital Frobenius algebra）と呼ぶことにします。通常のフロベニウス代数が単位／余単位を持つことを強調したいときは単位的フロベニウス代数ということにします。

パッヒナル移動（Pachner move）の星状細分（stellar subdivision）に対応する代数法則を（名前がないので）仮に星状律（stellar law）／余星状律（costellar law）と呼ぶことにします。チートシートに星状律／余星状律の絵があります。

単位的フロベニウス代数であれば、特殊律（これもチートシート）から星状律／余星状律が出ます（逆も真です）が、非単位的フロベニウス代数の場合は、星状律／余星状律を特殊律に置きかえることが出来ないので、そのまま星状律／余星状律を使います。星状律／余星状律を満たすことを単に「星状」という形容詞で表すことにすると、「パッヒナル移動不変な関手←→非単位的星状フロベニウス代数」という対応があります。

当記事冒頭「資料、訂正と結論」で述べたように、集合圏Setの可換群があれば、関係圏Relの非単位的星状フロベニウス代数が作れます。すべての非単位的星状フロベニウス代数が可換群に由来するかどうかは、僕は分かりません。また、単位的と非単位的なフロベニウス代数のあいだにどれほどの隔たりがあるかも分かりません。

ハイブの圏はなぜ3次元なのか

ハイブの圏Hiveには、次のような射（セル）があります。

• 点（建物としては柱）が0次元の射＝対象。
• 折れ線（建物としては幾つかのドアを持つ外壁）が1次元の射、折れ線の始点が域（ドメイン）、終点が余域（コドメイン）。
• ハイブが2次元の射。入口側外壁（折れ線）が域、出口側外壁（折れ線）が余域。
• ハイブのあいだの、三角形分割を保つ同相写像（とか、なめらか同相写像）と、パッヒナル移動を組み合わせた変形が3次元の射。変形前のハイブが域、変形後のハイブが余域。

0, 1, 2次元までは、圏の射としての次元と図形としての幾何的次元が一致しています。これは分かりやすい反面、誤解を招くかもしれません。圏としての次元と幾何的次元が一致している必要は全然ないのです。ハイブの圏ではたまたま一致しているだけです。

例えば、(1+1)次元コボルディズム圏では、1次元のコンパクト閉多様体が0次元の射＝対象で、2次元のコンパクト多様体が1次元の射です。2次元のコンパクト多様体のあいだの境界を固定してのなめらかな同相写像を2次元の射とすることもあります。要するに、図形としての次元と射としての次元は一致してません。別にかまいません。

圏としての次元は絶対的なものではなくて、用途により適当にズラシてもいいのです。いや、ズラシたほうがいいときがあります。例えば、既存のモノイド圏に、ダミーの0次元射＝対象を1個だけ追加して、それまでの対象を“ダミー対象を域・余域とする1次元射”に格上げします。射の次元も1だけ格上げすれば、圏全体の次元も1上がります。あるいは、n-射までしかない圏で、n-射のあいだの恒等(n+1)-射を追加すれば、(n+1)-射を持つことになり、これまた圏全体の次元は1上がります。

ハイブの圏Hiveの次元が3なのは、「次元が高めの射を入れたかった」という事情です。若干作為的な感じは否めません。Hiveの横結合は、一点（対象＝0-射）で繋ぐ（貼り合わせる）連接ですが、糊しろ（貼り合わる場所）を持たない併置を横結合にしても大差ありません。糊しろが空な貼り合わとは直和なので、直和をモノイド積とするモノイド2-圏（次元は1だけ落とす）をHiveとしても同じことです。

ネタ元（つうか、間接的なネタ元）がFHK論文であるので、2次元TQFT（Topological Quantum Field Theory）を多少は意識しています。しかし、ハイブの形状を平面領域（と同相な図形）から境界を許す2次元コンパクト多様体に一般化して、その上のTQFTモドキを作ろうと思うと、意外と面倒です。

分割の基本図形を三角形に限るのは辛くなるので、一角形、二角形も入れたほうがいいでしょう。対象である1次元コンパクト閉多様体に対応する恒等コボルディズムの構成のとき、線分（区間）と直積すると、三角形ではなくて四角形が現れたりするので、それの処理も面倒です。Hive（AKB12とほぼ同じ）がそうであるように、次元が退化した1次元図形もコボルディズムとして認めたほうがいいかも知れません。

どうするのがいいのかよく分かりません。ハイブはオモチャなので、あーでもないこーでもないと手でいじって遊べば、それでいいと思います。

よく分からんけど

僕は、物理に関する知識も素養も全くないので、聞きかじりとイイカゲンな類推で言うのですが： ゾンビフロー計算のセマンティクス（ディノテーション）をどうやって求めるかというと、事前に準備したゾンビ達を入口ドアに突入させて、ハイブ内部でワチャワチャ走らせて、十分に長い時間待ったときの、出口ドアへの散らばり具合を集計するわけです。

これって、S行列とかいうモノと似てんじゃないの？ よく知らんけど。それで、ゾンビフローのプロパゲーターがあって、離散時間（ステップ）で積み上げると長時間後のゾンビ配置パターン、出口からの出方のパターンが求まるような？

双対グラフが三価（2-in 1-out か 1-in 2-out）ではなくてニ価（1-in 1-out）でノード以外に開放端点・分岐点・合流点を持つなら、ノードの計算機能を成分とする行列Uを作って、Uⁿまたは(I + U)ⁿを計算すれば、遷移する系≒オートマトンの時間発展を追えます。ハイブは、対応する計算回路が三価グラフ（trivalent graph）なので、単なる行列ってわけにはいかないでしょう、たぶん。

単位時間（1ステップ）の時間発展を記述するには、マルチ射（オペラッドの射）、いや、ポリー射（多圏の射）みたいな計算デバイスが必要なのかな、よく分からんけど。

*1:単射（埋め込み）であることは引き続き仮定しているので、特異単体まで一般化はしてません。