このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

アレンジメント計算 3： 絵算の基本技法

雑記／備忘

「アレンジメント計算 1： 確率グラフィカルモデル」にて：

次回は、Arrgmnt(P) の代数構造について述べる予定です。

えーと、第3回ですが、まだ基本的な話が続きます。絵算の基本事項で、今まで（このブログでは）明示的に語ってなかったことを補足します。また、アレンジメント計算特有の描画法〈図法〉も説明します。

内容：

シリーズ第1回 兼 リンクハブ：

クラスター、ブラックボックス化、反ブラックボックス化

今、目の前にストリング図があるとしましょう。そのストリング図の一部分、つまり部分ストリング図〈subdiagram〉を“ひとまとまり”にしたいとき、当該の部分ストリング図を境界線で囲めばいいでしょう。こうやって識別した部分ストリング図をクラスター〈cluster〉と呼びます。

クラスターはGraphvizで使っている用語です。このご時世（つまり、新型コロナウィルス禍のなか）、「クラスター」には悪い印象が付着してしまいましたが、「何かが集まったかたまり」というだけです。一方、バーチャルSNS「cluster」というのが昨今流行っているようですね。僕もちょっと触ってみました（触っただけ）。

クラスター境界を描くには、線の色を変えたりするのが望ましいでしょうが、同色の実線で描いてもまー大丈夫でしょう。クラスターを不定形の領域にしてもいいですが、ノード形状（四角、三角、丸など）と同じ形状にしたほうが見やすいですね。クラスターの例を挙げます。念のため、クラスター境界線の色を赤にしています。

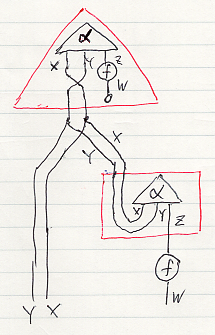
クラスターを作った後で、内部構造が見えないように塗りつぶしてしまうことがブラックボックス化〈blackboxing〉です。紙に手描きだと、ブラックボックス化したクラスターを縮小することは出来ませんが、ソフトウェアのお絵描きツールなら、ブラックボックス・クラスターをノードのサイズに縮小することができるでしょう。クラスターをノードとして扱えます。

ブラックボックス化したクラスター（ノードとみなす）を、もう一度内部構造が見えるようにすることが反ブラックボックス化〈unblackboxing〉です。これも、ソフトウェアなら「ノードアイコン ←→ クラスター領域」の展開・縮小のような形で実現できるでしょう。

ブラックボックス化したクラスターに名前を付けて保存しておくと再利用ができます。プログラミングにおけるマクロ定義とマクロ展開のようなものです。絵算ベースの証明支援系 Globular では、マクロ定義の集まり＝ライブラリを、アイコンパレットのUIとして提供しています。

オペレーターボックス

ストリング図において、関手をボックスやストライプで表すことがあります。関手ボックスや関手ストライプ〈関手シース〉に興味があれば：

関手に限らず、圏論的コンストラクタ／オペレーターをボックスで表すことができます。モナドを拡張スタイルで定義するときの拡張オペレーター〈クライスリ・オペレーター〉をボックスで描いた例は次の記事にあります。

そもそも、コンストラクタやオペレーター（コンビネータとも呼ぶ）が何であるかは次の記事を見てください。

コンストラクタ／オペレーターの例を挙げておきましょう。これらのコンストラクタ／オペレーターが今すぐ必要ってわけではありませんがね。

  1. コンパクト閉圏の双対化コンストラクタ
    |C|∋A \mapsto A*∈|C|
  2. デカルト閉圏の内部ホム・コンストラクタ
    |C|×|C|∋(A, B) \mapsto [A, B]∈|C|
  3. デカルト閉圏の評価射オペレーター
    |C|×|C|∋(A, B) \mapsto (evA,B:[A, B]×A → B in C)
  4. トレース・オペレーター
    |C|×|C|×|C|∋(X, A, B) \mapsto (TrXA,B:C(A\otimesX, B\otimesX) → C(A, B) in Set)
  5. 不動点オペレータ
    |C|×|C∋(X, A) \mapsto (FixXA:C(A\otimesX, X) → C(A, X) in Set)
  6. デカルト微分コンビネータ
    |C|×|C|∋(A, B) \mapsto (DA,B:C(A, B) → C(A×L(A), L(B)) in Set) （Lは線形化コンストラクタ）
  7. カリー化オペレーター
    |C|×|C|×|C|∋(A, B, C) \mapsto (CurryA,B,C:C(A×B, C) → C(A, [B, C]) in Set)
  8. デカルト・ペアリング
    |C|×|C|×|C|∋(X, A, B) \mapsto (PairX,A,B:C(X, A)×C(X, B) → C(X, A×B) in Set)

S, T が |C|×|C| → |D| のコンストラクタで、αが |C|×|C|∋(A, B) \mapsto (αA,B:C(A, B) → D(S(A, B), T(A, B)) in Set) の形のオペレーターのとき、α(f:A → B in C):S(A, B) → T(A, B) in D を次の形で描きます。

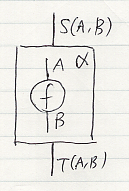
'α'とラベルされたボックスの内部はCで、ボックスの外部がDになります。

アレンジメント計算のオペレーター

C = (C, \otimes, 1, σ, Δ, !) は条件化可能マルコフ圏とします。話を簡単にするために、Cは（モノイド圏として）厳密モノイド圏としておきます。今回はモノイド多圏は出しません*1。

条件化可能マルコフ圏は、「ベイズ確率論とデータベース理論の統合： カップル化可能圏」で述べたカップル化可能圏の公理を満たし、Couple(C) を作ることができます。また、「アレンジメント計算 1： 確率グラフィカルモデル」で述べた Relev(C) := 1/C も作れます。

アレンジメント計算で出てくるオペレーター〈コンビネータ〉は次のものです。

オペレーター名 略記 プロファイル
左条件化 LConditA,B ∪(-) Couple(C)(A, B) → Relev(C)(A, B)
右条件化 RConditA,B (-)∪ Couple(C)(A, B) → Relev(C)(B, A)
左同時化 LJointA,B ∩(-) Relev(C)(A, B) → Couple(C)(A, B)
右同時化 RJointA,B (-)∩ Relev(C)(A, B) → Couple(C)(B, A)
反転 ConvsA,B (-)† Relev(C)(A, B) → Relev(C)(B, A)

このなかで本質的なものは条件化オペレーター LCondit = Condit だけです。他のオペレーターは、マルコフ圏に備わった演算と Condit から構成できます。実際には、これらのオペレーターは関手（反変関手もある）になります -- それは事後的に分かることです。

これらのオペレーターをボックスで描くときは、オペレーター名ではなくて略記の演算子記号でラベルすることにします。ボックス内でのラベルの位置は：

  • ∪(-) ボックスの左下
  • (-)∪ ボックスの右下
  • ∩(-) ボックスの左上
  • (-)∩ ボックスの右上
  • (-)† ボックスの右上

次のようですね。

オペレーターをワイヤー曲げ〈wire bending〉で描くと、ボックスの中と外がシームレスに繋がり、オペレーターボックスはクラスターボックスとして扱うことができます。例えば次のようです。

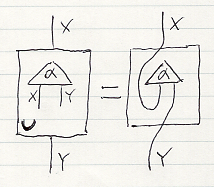
さらに、クラスターボックスを省略しても問題ありません。

確率空間と注釈ボックス

条件化可能なマルコフ圏Cが、ジリィモナドをベースに構成した確率的圏である状況考えましょう。“C内の確率空間”の概念が重要です。確率空間は、Cの対象 A と、ω:1 → A in C の組 (A, ω) です。これを、いつものように記号の乱用で A = (A, ω) のように書くのは一旦やめて、X = (A, ω) のように書きます。あるいは、使う文字が増えすぎないように、X = (X, μX) と書きます。

  • Xは、確率空間Xの台可測空間
  • μXは、確率空間Xの確率測度

確率空間と関連〈relevance〉（確率測度を保存する射）の図示を説明します。実例無しでルールだけ述べてもピンとこないでしょうが、後で参照するためにルールを書いておきます。

X = (X, μX) を図に描くときは次のようにします。

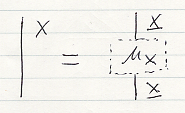
点線で囲まれた箱を注釈ボックス〈annotation box〉と呼ぶことにします。ワイヤーとそれに付いた注釈ボックスの情報により確率空間が表現されます。ワイヤーは、注釈ボックスの下側だけ、上側だけでもかまいません。

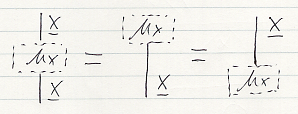
Cの射 f:X → Y in C が確率測度を保存すること（fが関連であること）は次のように描きます。

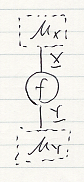
域側に注釈ボックスを付けるだけでもいいとします（余域側注釈ボックスはオプショナル）。

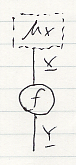
実際には、注釈ボックス内にも絵を描きます。

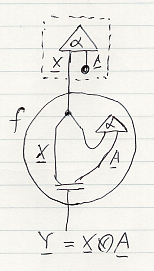
この図には、様々な描画法が使われています。上側の点線の箱は注釈ボックスで、全体として関連を図示しています。fはクラスターで、クラスター境界は丸で描かれています。カップ状（∪）に曲がったワイヤーは条件化コンビネータの略記です。長めのイコール記号は「Y = X\otimesA」という等式（念のためにテキストでも書いてある）を図中に埋め込んだものです。この図は豊富な情報を持ちますが、それでもまだ書き切れてない事項や注意すべき事は残っています（そこらへんはいずれ）。

おわりに

オペレーターボックスの簡潔な表現であるワイヤー曲げと、確率空間の構造を表す注釈ボックスを使うと、条件化可能マルコフ圏Cに付随する圏 Couple(C)、Relev(C) での絵算が捗ります。

*1:ストリング図を描くと、潜在的に簡約多圏（対象がリストである圏）を使ってしまうのですけどね。