アレンジメント計算 4：アレンジメント - 檜山正幸のキマイラ飼育記 (はてなBlog)

アレンジメントは、三角形*1から何本かの脚が生えた図形、そしてその図形で表現される圏論的対象物です。今回はアレンジメントに対する操作と、その操作の絵図表現／テキスト表現について説明します。

この記事での図の描画方向は「アレンジメント計算 1：確率グラフィカルモデル // アレンジメントとアレンジメント図」で述べたように上から下です。

内容：

アレンジメントの表記
マルコフ多圏の基本構造射
スパイダー射とその表現
アレンジメントへのスパイダー作用
アレンジメントの周辺化
アレンジメントの二部化と二部アレンジメント
おわりに

シリーズ第1回兼リンクハブ：

アレンジメント計算 1：確率グラフィカルモデル

アレンジメントの表記

Cは条件化可能マルコフ圏とします。Cから標準的に構成したマルコフ多圏（簡約多圏）をPとします。CよりPを使う理由は主に次の2つです。

Pの対象は、Cの対象からなるリストなので、入出力が“多変数”である射を自然に扱える。
Pは、モノイド圏として厳密モノイド圏なので、モノイド積の扱いが簡単になる。

C, P の対象・射・結合・恒等射・モノイド積などには、特に変わった記法を使わず、普通の記号を使います。どういうことかと言うと：

Cが具体的な確率的圏のときは、射（マルコフ核）を大文字で書き、結合・恒等射の記号にそれぞれ ';;'または' $\odot$ '、'kid'または'Id'を使ったが、そういうことはしない。
Pの対象はリストなので、リストであることを強調する目的で A, B のように下線を引いたことがあるが、そいういうことはしない。
Pの対象はリストで、対象のモノイド積はリストの連接で与えられるので、モノイド積の記号に連接の記号 '#' を使ったことがあるが、そういうことはしない。

ただし、Pのモノイド単位対象は () と書くことにします。Cのモノイド単位対象は 1 です。Pは厳密モノイド圏なので、次の等式が厳密に（圏論の意味での strictly）成立します。

For A, B, C∈|P|, (A $\otimes$ B) $\otimes$ C = A $\otimes$ (B $\otimes$ C)
For A∈|P|, () $\otimes$ A = A
For A∈|P|, A $\otimes$ () = A

Pの対象 A は、A = (A₁, ..., A_m) のように書きます。このとき、A₁, ..., A_m はそれぞれCの対象です。

Pのアレンジメントωとは、ω:() → A in P という射です。したがって、

Arrgmnt(P) := {f∈Mor(P) | dom(f) = ()}

アレンジメントωを、ω = (A, ω) と書くことがあります。これは、よくある記号の乱用とは違います。(A, ω) は冗長な書き方になっているだけです。なぜなら、ωが分かれば A = cod(ω) なので、(cod(ω), ω) は冗長です。ω = (A, ω) と書くのは、アレンジメントωを確率空間ともみなしたいからです。

アレンジメント ω = (A, ω) に対して、legs(ω) := cod(ω) = A, nlegs(ω) = length(legs(ω)) と定義します。lengthはリストの長さを返す関数です。脚の本数〈number of legs〉 nlegs(ω) はアレンジメントにとって重要な量で、次が成立します。

nlegs(ω) = 0 ⇔ ω = id₍₎

ところで、アレンジメントを絵に描くとクラゲに似てますよね。

マルコフ多圏の基本構造射

マルコフ圏Cにおいて、対象 A, B C に対する α_A,B,C, λ_A, ρ_A, σ_A,B, Δ_A, !_A は定義から明らかです。Cに対応するマルコフ多圏Pにおいて、同じ記号が何を意味するかを確認しておきましょう。

Cの対象からなるリスト A = (A₁, ..., A_m) があるとき、（モノイド積に関する）総積 Π(A) は次のように定義されます。

Π(A) = Π((A₁, ..., A_m)) = A₁ $\otimes$ ... $\otimes$ A_m ∈|C|

m = 0, 1 のときは、

Π(()) = 1 ∈|C|
Π((A₁)) = A₁ ∈|C|

Pのホムセットは、Cのホムセットを使って定義されました。

P(A, B) := C(Π(A), Π(B))

ただし、この定義のまんまだと、Pのホムセットが重なって〈交わって〉しまいます。それに対する対処は次に記事に書いてあります。

ホムセットは交わるのか

対処をして、Pのホムセットの重なりはないとします。

マルコフ多圏Pは、モノイド圏として厳密モノイド圏なので、モノイド圏の構造射（の族） α, λ, ρ は恒等射になります。残る基本構造射 σ, Δ, ! を定義しましょう。

A, B は（Cの対象からなる）リストだとして、σ_A,B, Δ_A, !_A のプロファイルは次のようになります。

σ_A,B:A $\otimes$ B → B $\otimes$ A in P
Δ_A: A → A $\otimes$ A in P
!_A: A → () in P

ほんとは σ_A,B = σ_Π(A),Π(B), Δ_A = Δ_Π(A) ではありませんが、Π(A) $\otimes$ Π(B) $\cong$ Π(A $\otimes$ B) などの同型を介して同一視すれば、今の等式が成立すると思って差し支えありません。!_A = ！_Π(A) は等式として成立しています。

とはいえ、!_A = ！_Π(A) も「ホムセットは交わるのか」の対処まで考えるとやっぱりほんとのイコールじゃないです。P(A, B) = C(Π(A), Π(B)) という前提でのイコールです。ウーム、イコールの話は難しいなー。柔軟・臨機応変に、同一視と区別を切り替える必要があります。

スパイダー射とその表現

マルコフ圏Cにおいて、id, α, λ, ρ, σ, Δ, ! に適切に下付き添字を付けたモノ達は、Cの射の集合になります。この射の集合から（結合とモノイド積で）生成されたCの部分モノイド圏を Spid(C) と書き、Cのスパイダー圏〈spider category〉と呼びます。Cのスパイダー圏 Spid(C) は、Cの広い部分圏〈{wide | broad} subcategory〉（親の圏と同じ対象類を持つ部分圏）です。スパイダー圏 Spid(C) の射をスパイダー射〈spider morphism〉、あるいは単にスパイダーと呼びます。

何をスパイダーとして選ぶかはケースバイケースですが、マルコフ圏では上記の定義が標準的でしょう。例えば、ハイパーグラフ圏（「ハイパーグラフ圏一瞥」参照）なら、さらに ∇（余対角、余乗法）、i（余単位）もスパイダーの仲間に入れるでしょう。

マルコフ多圏Pにおいては、α, λ, ρ は意味がなくなるので（厳密モノイド圏だから）、id, σ, Δ, ! から生成された部分モノイド圏が Spid(P) です。Spid(P) の射、つまりスパイダーの一例を挙げます。

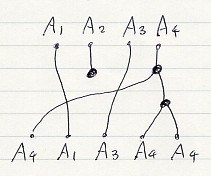
上の図のような、スパイダー射を表すストリング図をスパイダー図〈spider diagram〉と呼びます。ひとつのスパイダー射を表すスパイダー図は一般にはたくさんあります。逆向き「スパイダー図 → スパイダー射」の方向の対応ならば一意に決まります。

スパイダー射をスパイダー図で表すのは分かりやすくて良いのですが、毎回絵を描くのはめんどうです。スパイダー射を、非常に効率的にテキスト表示する方法があります。その表示には番号列を使います。

Seq(n) := List({1, ..., n}) と定義します。特に Seq(0) = {()}, Seq(1) = {(), (1), (1, 1), ...} $\cong$ N です。Seq(n) の要素は、単に正整数のリストに過ぎませんが、特定の目的で使用するので番号列〈index number sequence | sequence of index numbers〉と呼ぶことにします。

s:A → B in Spid(P) で、A = (A₁, ..., A_m), B = (B₁, ..., B_n) のとき、番号列 X = (X₁, ..., X_n) ∈Seq(m) があり、sは、AとXで完全に決定されます。Seq(m) の番号列で長さがnのモノの集合を Seq_n(m) とすると、次の同型があります。

Spid(P)(A, B) $\cong$ Seq_n(m) where m = length(A), n = length(B)

この同型をちゃんと示すには、組み合わせ的議論をしなくてはならず、けっこうめんどうですが、実例で見れば直感的に明らかだと思います*3。

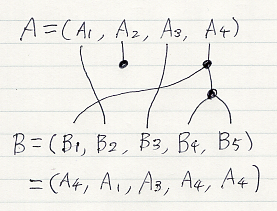
この例で言えば、図のスパイダー射を表す番号列Xは、X = (4, 1, 3, 4, 4) となります。

域が A = (A₁, ..., A_m)∈|P| で、番号列Xで表されるスパイダー射を σ^A_X と書くことにします -- すべてのスパイダー射はこの形に表示できます。

アレンジメントへのスパイダー作用

マルコフ多圏Pも当然ながら圏なので、圏の結合〈composition〉があります。それを、comp:Mor(P)×Mor(P) ⊃→ Mor(P) とします。記号'⊃→' は部分写像であることを意味します。すべてのペア (f, g)∈Mor(P)×Mor(P) に comp(f, g) = f;g が定義できるわけではありません。

Arrgmnt(P) ⊆ Mor(P), Mor(Spid(P)) ⊆ Mor(P) なので、comp を Arrgmnt(P)×Mor(Spid(P)) ⊃→ Arrgmnt(P) に制限することができます。この制限された写像を次のように書き、（アレンジメントへの）スパイダー作用〈spider action〉と呼びます。

spidAct:Arrgmnt(P)×Mor(Spid(P)) ⊃→ Arrgmnt(P)

スパイダー作用は、圏の結合に過ぎないので、spidAct(ω, s) = ω;s と書きます。次の等式が成立します。

For ω∈Arrgmnt(P), id_A∈Mor(Spid(P))
ω;id_A = ω where A = legs(ω)
For ω∈Arrgmnt(P), s, t∈Mor(Spid(P))
(ω;s);t = ω;(s;t)

「左右」の別は書き方に影響されますが、今使っている図式順記法で言えば、集合 Arrgmnt(P) に、圏 Spid(P) が右から作用していることになります（反図式順記法なら「左から」）。

スパイダー作用とは何かと言えば；アレンジメントの脚を、入れ替える、断ち切る、分岐させる操作を何度か行うことです。脚だけ操作するので“本体”に変化はなく、同じモノが違った見え方で現れることになります。アレンジメントを現象のモデルとすると、脚の形が現象の見え方を制御しているのです*4。

さて、スパイダー s∈Mor(Spid(P)) は、A = dom(s) と番号列 X∈Seq(m) where m = length(A) で、s = σ^A_X と書けるのでした（前節）。この事実を背景として、次の略記を導入します。

ω[X] := ω;σ^A_X = ω;s where A = legs(ω) = dom(s)

例えば、X = (4, 1, 3, 4, 4) なら、ω[(4, 1, 3, 4, 4)] = ω;σ^A_{(4, 1, 3, 4, 4)}。ブラケット〈角括弧〉の内側の丸括弧は省略して、ω[4, 1, 3, 4, 4] := ω[(4, 1, 3, 4, 4)] のように書きます。ブラケットに入れた番号列により、任意のスパイダー作用を表現できます。

また、マルコフ多圏Pの対象であるリスト A に対して、

A[X] := cod(σ^A_X)

と定義します。例えば、(A₁, A₂, A₃, A₄)[4, 1, 3, 4, 4] = (A₄, A₁, A₃, A₄, A₄) です。下付き添字が入れ子にならないように、X_i を X(i) と書くことにすると：

A[X] := (A_X(1), ..., A_X(n))

アレンジメントωが、ω:() → A in P ならば、

ω[X]:() → A[X] in P

です。

アレンジメントの周辺化

C, P が具体的な確率的圏／多圏であるとき、Pのアレンジメントは同時確率分布を表します。同時確率分布に対して、その周辺確率分布を求めることはしばしばあります。周辺確率分布を求める操作に対応する圏論的オペレーターを周辺化〈marginalization〉と呼びます。周辺化は、スパイダー作用の特別なものです。

番号列 X∈Seq(m) に対して、一意〈unique〉、単調〈monotone〉という性質を次のように定義します。

Xは一意である :⇔ i, j∈N に対して、i ≠ j ならば X(i) ≠ X(j) （意味を持つ i, j に対して）
Xは単調である :⇔ i, j∈N に対して、i ≦ j ならば X(i) ≦ X(j) （意味を持つ i, j に対して）

一意な番号列の全体を USeq(m)、単調な番号列の全体を MSeq(m)、単調一意な番号列の全体を MUSeq(m) と書くことにします。次の同型は簡単に分かるでしょう。Pow(-) はベキ集合です。

MUSeq(m) $\cong$ Pow({1, ..., m}) in Set

ω:() → A in P はm脚のアレンジメントとして、X∈MUSet(m) とします。このときのスパイダー作用（の結果） ω[X]:() → A[X] in P が、ωのXによる周辺化です。例えば、ωが4脚のときは、ω[1, 2], ω[2, 3, 4], ω[3] などはωの周辺化です。ω[] = ω[()], ω[1, 2, 3, 4] も周辺化ですが、ω[] = id₍₎, ω[1, 2, 3, 4] = ω なので面白くはありません。

i∈{1, ..., m} に対する ω[i] = ω[(i)] は、ω[i]:() → A[i] in P で、A[i] = A[(i)] = (A_i) ですから、ω[i]:() → (A_i) in P となります。通常「周辺確率分布」というと、ω[i] のことを意味することが多いのかも知れません。

単調一意な番号列Xによるアレンジメントの周辺化 ω[X] とは、Xに出現しない脚をすべて断ち切ってしまうことです。脚の断ち切りは、マルコフ圏の破棄射を脚に結合することです。具体的な確率的圏では、総和や積分を用いて破棄射の計算をします -- それは、通常の周辺確率分布を求める手順に一致します。

アレンジメントの二部化と二部アレンジメント

ω:() → A in P はm脚のアレンジメントとして、0≦ k ≦ m である自然数 k を境い目として、アレンジメントの脚を前半〈左側〉ｋ本と後半〈右側〉(m - k)本の二グループに分けることを、アレンジメントの二部化〈bipartitioning〉と呼びます。例えば、4脚を左の1脚と右の3脚に分けることができます。

ωの脚が (A₁, ..., A_m) のとき、二部化された脚は ((A₁, ..., A_k), (A_k+1, ..., A_m)) のように書けます。入れ子のリストは鬱陶しいので、区切り記号'&'を使って、(A₁, ..., A_k & A_k+1, ..., A_m) と書くことにします。

ω:() → A in P にスパイダーを作用させた後に二部化することを、'&'で区切りを入れた番号列で表現できます。例えば、ω[4, 1 & 3, 4, 4] とかです。絵に描くときも、ワイヤー達を'&'で左右に分割することにします。

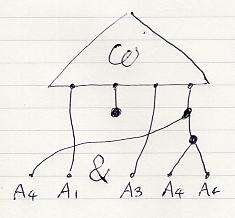
脚が二部に分けられたアレンジメントを二部アレンジメント〈bipartite arrangement〉と呼びます。m脚のアレンジメントからは、(m + 1)個の二部アレンジメントを作れます。

おわりに

アレンジメントに対する操作として、スパイダー作用と二部化を紹介しました。スパイダー作用は脚の入れ替え／断ち切り／分岐をします。二部化は脚達を前後（あるいは左右）の二グループに分ける操作です。次回は、より重要なアレンジメント操作であるリンク積について述べる予定です。予定は変わるかも知れませんが。

*1:三角形であることに何の意味もないのですが、多くの人が三角形で描くのは事実です。

*2:画像：https://illustimage.com/?dl=11603

*3:スパイダー射の表示（スパイダー図の正規形）が一意に決まることを主張する定理を一般にスパイダー定理と呼びます。マルコフ圏のスパイダー射と番号列の同型も一種のスパイダー定理です。

*4:グラフィカルモデルなどでは、個々の脚に相当するモノを“確率変数”と呼んでいます。アレンジメントは“幾つかの確率変数の集まり”ということになります。