比較的最近、「絵算のススメ 2015 年末版」という記事を書きました。なぜ絵算をおススメするのかというと、計算や証明がとても簡単になる(ことがある)からです。
テキスト記法だとけっこう面倒な計算が、絵算では自明になってしまう例を紹介します。
内容:
こんな例題
次のラルフ・ヒンズの論文から命題を2つ選んで、それを例題にします。
- Title: Theoretical Pearl / Monads from Comonads, Comonads from Monads / An Exercise in Program Transformation
- Author: Ralf Hinze
- URL: http://www.cs.ox.ac.uk/ralf.hinze/WG2.8/28/slides/Comonad.pdf
- Pages: 11p.
内容はともかくとして、とりあえず、どのくらい短く単純になるかを見てもらいましょう。説明は後回しです。
ヒンズ論文の引用は、記号を書き写すのが面倒だったので画像を貼ってあります。対応する絵算は、僕の手描きをスキャンした画像です。絵算の部分では、コロンの左側に命題の主張をテキストで書いてあり、コロンの右側が絵です。テキスト記法もヒンズのものとは違います。TeXコマンドなしでも書けて絵算と相性が良い記法に直しています。
まずは、ヒンズ論文p.3からp.4の命題。
テキストによる等式的変形:


対応する絵算(ストリング図):
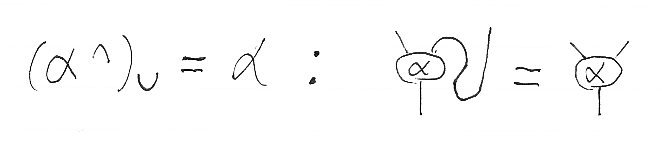
次に、ヒンズ論文p.5の命題です。
テキストによる等式的変形:

対応する絵算(ストリング図):
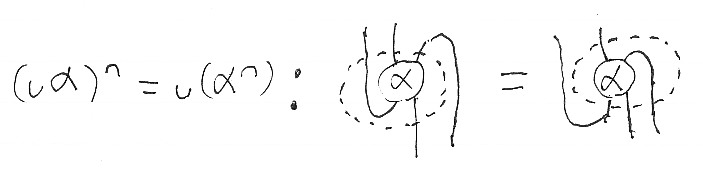
ヒンズ論文では、定義や法則を引用しながら、何段階かの等式的変形(equational reasoning)をしてますが、絵算では描いてしまえば一目瞭然、特に計算・証明すべきことはありません。何もしなくても命題は明らかだと判断できます。
何を説明するのか
前節の2つの命題は次でした。今は意味不明でかまいません。
- (α∩)∪ = α
- (∪α)∩ = ∪(α∩)
一番目の等式の絵は、ニョロニョロ関係式を使ってワイヤーの引き伸ばしをしてますが、ニ番目の等式では何もしません。「あー、確かに等しいね」と目視確認するだけです。なので、絵の等式は左右が同じトートロジーになっています。一応、最初に注目する場所が違うことを示すために、点線枠が描かれていて、この枠(目線のガイド)は等号の左と右で違います。
「何もしなくても分かってしまう」ので、ニ番目の等式のほうが絵算の威力を示すのに好都合です。というわけで、二番目の等式について詳しく説明して、一番目は最後に触れます。
ヒンズのオリジナルの記法と僕の記法が違うので、その対応を示します。∩と∪を添字に使う書き方は「アブラムスキーのネームとかフリップとか」で使ったものです。
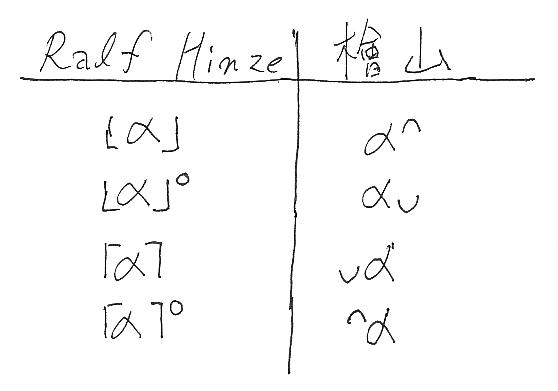
描き方・書き方の約束
圏はイタリック体の英字大文字、関手は通常体の英字大文字、自然変換はギリシャ文字小文字で表します。絵でもテキストでも、方向はすべて左から右に統一します。絵の縦方向は上から下の順序です。より具体的には:
- 関手Fの後にGを結合したものは F*G と書く。混乱の恐れがなければ、併置 F G (区切りの空白あり)または FG を使う。
- 自然変換αの後にβを横結合したものは α*β と書く。混乱の恐れがなければ、併置 α β (区切りの空白あり)または αβ を使う。
- 自然変換αの後にβを縦結合したものは α;β と書く。絵では、αが上、βが下の位置に描く。
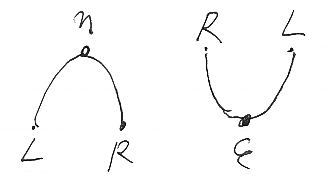
L, R, η, ε はヒンズ論文と同じ意味で使います。つまり:
- 関手 L:D→C と R:C→D は随伴ペアで、Lはペアの左相方*1、Rはペアの右相方。C(L(X), B)
D(X, R(B)) が成立している。
- 自然変換ηは随伴ペアの単位で、η::IdD⇒L*R:D→D 。
- 自然変換εは随伴ペアの余単位で、ε::R*L⇒IdC:C→C 。
この状況を絵で描けば次のようです。もう一度繰り返しますが、テキストも絵も、左から右、上から下です。
圏はCとDしか出てこない(しかも C = D の状況が多い)ので、絵に圏の名前を書き込んではいませんし、マースデンのような色も使ってません。が、曖昧性や混乱はないと思います。
文字 F, G, α, β は文脈に応じて適当に選ぶ関手/自然変換として使います。
絵の描き方の基本は(いくつかの変種がありますが)、「絵算のススメ 2015 年末版」で紹介したマースデンの論説の第2章"An Outline of the Graphical Approach"に書いてあります。マースデンの絵の方向は下から上なので注意して下さい(横方向は左から右)。
http://www.euclideanspace.com/maths/discrete/category/principles/string/index.htm には絵算のチートシートがあります。絵が小さく、ページのデザインがいまいちですが、拡大して見ればいいでしょう。ここの絵は、左から右/上から下なのでこの記事(檜山の描き方)と同じ方向です。
関手を折り曲げる
記号 α∩ と ∪α を定義しましょう。次のとおりです。
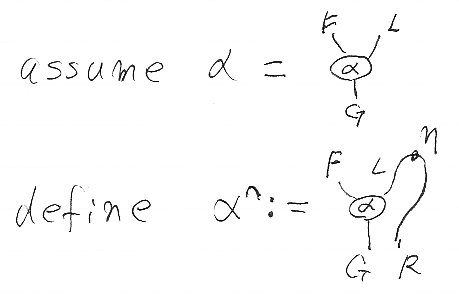
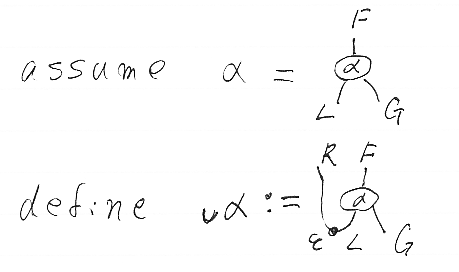
α∩ は、α::F*L⇒G:E→C (Eは何か適当な圏)に対して定義されます。(F:E→D、G:E→C は容易に推測できます。)自然変換αに働くオペレータ (-)∩ は、αの右入力である関手Lを曲げる(bend)操作です。随伴の単位εを繋げることによって折り曲げ(bending; 曲げ加工)を実現してます。Lを折り曲げた後は、α∩::F⇒G*R:E→D となります。
α∩ を定義している絵(ストリング図)をテキストに書き出してみましょう。そのためには、絵の各部分(ピース)を、四角いコマに分割します。コマは、レゴやラキュー(LaQ)のブロック、ドミノや麻雀の牌みたいなもんだと思えばいいでしょう。
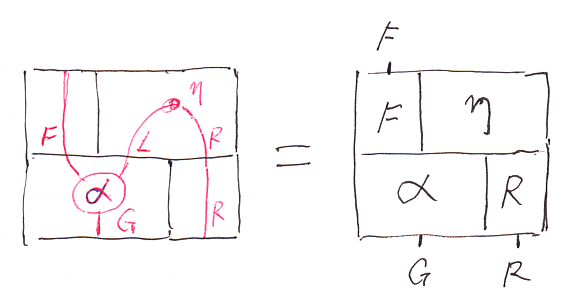
α∩ は、F、η、α、Rの4つのコマが組み合わさったモノです。横に並べる操作(横結合)を「*」(アスタリスク)、縦に並べる操作(縦結合)を「;」(セミコロン)で表す約束だったので、
- α∩ := (F*η);(α*R)
です。∪α も同様にして、
- ∪α := (R*α);(ε*G)
と書けます。
同じだから同じ
αが、次の絵のように、F*L⇒L*G:D→C の形をしているなら、(∪α)∩ も ∪(α∩) も定義できます。
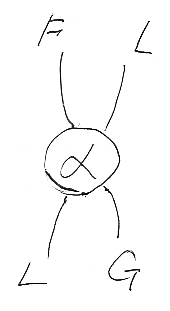
(∪α)∩ = ∪(α∩) を確認するのに、「絵算では計算や証明など必要ない」と言いました。(∪α)∩ の絵と ∪(α∩) の絵を描いてみると、同じになるので、「あー、同じだね」としか言いようがないのです。
(∪α)∩ も ∪(α∩) も次のように9個のコマをキッチリ並べて作られるモノです。
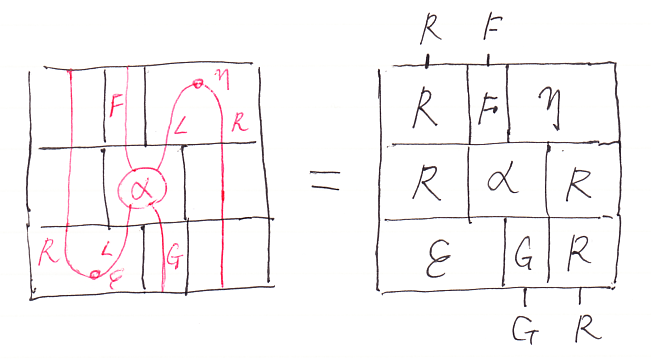
9個のコマの縦横並びを書き下すと、(R*F*η);(R*α*R);(ε*G*R) です。つまり、
- (∪α)∩ = (R*F*η);(R*α*R);(ε*G*R)
- ∪(α∩) = (R*F*η);(R*α*R);(ε*G*R)
だから、(∪α)∩ と ∪(α∩) は同じです。
どうしてテキストだと計算や証明が必要になるのか
絵算に慣れると、テキストの計算が何やってるか理解できなくなる弊害もあります。テキストでは、絵のわずかなレイアウト変更も計算ステップになります。そればかりか、目視の注目箇所や目線移動も明示的に計算に入れる必要があります。
今の例だと、左下から右上(またはその逆)への目線移動、つまり視覚的認識の時間順序までテキストに書き下して等式に関する論理(equational logic)で変形する必要があります。具体的に言うと、左下の R, α, ε, G で構成される四角形を先に見るか、右上の F, η, α, R で構成される四角形を先に見るかの違いが、計算・証明すべき内容になります。
記述を簡略化するために、番号を振ったコマを使うことにします。
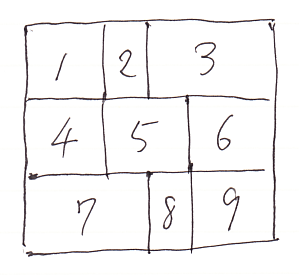
コマを、[1], [2] などと書くことにして、全体は次のように表せます(横結合のアスタリスクは省略して単に併置にしました)。
- ([1][2][3]);([4][5][6]);([7][8][9])
左下の四角形は、([4][5]);([7][8]) と書けます。その右隣は、[6];[9] です。上段は [1][2][3]、このような配置順序を意識して書き下すと、
- ([1][2][3]);( ( ([4][5]);([7][8]) )([6];[9]) )
一方、右上の四角形 ([2][3]);([5][6]) を先にひとかたまりと認識するなら、
- ( ([1];[4])( ([2][3]);([5][6]) );([7][8][9])
どの場所を“かたまり”と認識するか(注目箇所)や認識順序(目線移動)は自由であることは、横結合の結合律、縦結合の結合律、そして交替律によって保証されます。
絵算では、注目箇所の選択と目線移動によりほぼ一瞬で認識できる事実を、テキスト計算では、各種の法則による項の書き換えを律儀に遂行して示さなくてはなりません。もともと2次元的な計算を、シリアライズして1次元テキストにしているので、計算の見通しが立ちにくいのも難点です。計算に関与するすべてのモノ(関手や自然変換)に名前を付けて、それを覚えておかなくてはならないのも負担です*2(絵では、名前を大幅に省略します)。
「絵算が便利」と言うよりは、2次元計算に対しては「1次元化したテキスト計算が非効率的で不便過ぎる」というのが実状だと思います。
レイアウト変更と引き伸ばし
最後に、(α∩)∪ = α を例にしてレイアウト変更と引き伸ばしについて説明します。
絵算とテキスト計算の中間である象形文字計算(笑)も使います。象形文字としての「∩」は随伴の単位、「∪」は余単位、「|」は適当な関手(名前は省略)を表します。この象形文字を使うと、α∩ と β∪ は次のように書けます。
- α∩ := (I∩);(αI)
- β∪ := (βI);(I∪)
βにα∩を代入すると、
- (α∩)∪ := ( ((I∩);(αI)) I );(I∪)
ウーン、象形文字、そんなに分かりやすくないかな? 次のようなことです。
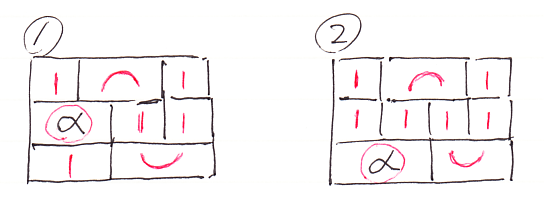
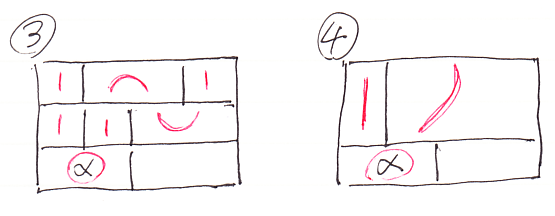
(1)が (α∩)∪ の絵です。(1)の左下四角形に α;I = II;α を適用すると、(1)から(2)に変形できます。(2)の右下四角形を II;∪ = ∪ により置き換えると、(2)から(3)が出ます。(3)の右上四角形はニョロニョロカーブの形 (∩I);(I∪) なので引き伸ばせばIになり、(4)となります。この(4)はαそのものです。
ここでは、ワイヤーを伸ばしたり縮めたりしてレイアウト変更をしています。ワイヤーが伸縮自在なのは、圏の恒等射はいくら付け足しても削っても同じだからです。最後のニョロニョロカーブの引き伸ばし(stretching)は、随伴の性質です。随伴(双対)の本質は、「S字状のカーブは引き伸ばせて、真っすぐになるよ」ということでした(「ニョロニョロ」の検索)。
以上けっこう丁寧に説明しましたが、事情を分かっているなら冒頭に示した記述(再掲↓)でも十分でしょう。

絵算の問題点
使える場面では絶大な威力を発揮する絵算ですが、使えないこともママあります。また、無理に使うとテキスト計算よりかえって面倒になるなんて本末転倒なことも。
それと、絵を描く良いツールがないのも問題です。組版や出版の技術はテキストに最適化されているので、構造的な図版を取り扱うウマい方法がありません。
「作って・操作して・配布する」効率的な手段がないと、やはり敷居が高くなります。パワー(John Power)が、"2-Categories"という論説のなかで、絵(図版*3)が入ってない言い訳みたいな口調で次のように書いてます。
(意訳) 私はLaTeXスキルがアレなもんで、絵を入れてないんだ、ゴメンね。昔はさ、自分でLaTeXで苦労したりしなくても秘書がタイプしてくれたんだよね。手描きの絵もOKだったし。そういう良き時代の論文には良い絵が載ってるし、紙や黒板に手描きするときも絵は役に立つよ。
We have mentioned many pictures in the above analysis. We have not drawn them owing to my mediocre latex skills. However, they are well worth using, at least on paper and on blackboards; and the 2-category literature is full of them, especially in older papers for which secretaries did the typing, and when journals accepted hand-drawn figures.
ストリング図(それと可換図式)のツールが出現しないとこの問題は解決しないでしょうね*4。それまでは、手描きとスキャナかなぁー。
*1:相方は、ペアの片一方の意味で使っています。英語のadjoint mateには別な意味があります。
*2:[追記]次元が高くなると、名付けの負担はトンデモナイものになります。「続・2次元の圏のための記号法」を参照。名前無しで計算する方法がないと行き詰まります。[/追記]
*3:可換図式も含みます。
*4:[追記]サイモン・ウィラートン(Simon Willerton)が n-Category Cafe で、サーフェイス図を作って利用するウマい方法がないもんかなー、みたいなことを書いてます。 [/追記]