余モナドにおけるパンツマジックとシングレット - 檜山正幸のキマイラ飼育記 (はてなBlog)

反ラックス・モノイド余モナドの計算（ストライプ図絵算）をゴニョゴニョしているときに気付いた等式があります。とりあえずその等式を、余モナドのパンツマジック等式〈pants magic equation〉と呼んでおきます。ストライプ図を眺めると、下着〈パンツ〉の上にズボン〈パンツ〉を履いていたのに下着だけになってしまうマジックに見えるからです。

ある観点から見ると、パンツマジック等式は自明な等式でした -- 「なーんだ」という気分になりました。なので、この記事はボツにしようかとも思ったのですが、ゴニョゴニョの過程がまったく無意味というわけでもなさそうです。余クライスリ圏 ${_\boldsymbol{F}\mathcal{C}}$ の計算をもとの圏 $\mathcal{C}$ で行うとき、パンツマジックに関連する技法や概念が使えます。計算練習／計算事例として多少の意味はあるでしょう。 $\newcommand{\Arr}{\:\downarrow } \newcommand{\twoTo}{\Rightarrow } % \newcommand{\coM}{\boldsymbol{d} } % comultiplication \newcommand{\coU}{\boldsymbol{e} } % counit \newcommand{\Ev}{\mathrm{Ev} } \newcommand{\gcoM}{\bar{\boldsymbol{\delta}} } % generic comultiplication \newcommand{\oast}{\circledast } % \newcommand{\In}{\text{ in } } %\newcommand{\hyp}{\text{-} } \newcommand{\id}{\mathrm{id}} \newcommand{\Ev}{\mathrm{Ev}} %\newcommand{\ev}{\mathrm{ev}} %\newcommand{\moveTo}{\rightsquigarrow } %\newcommand{\Iff}{\Leftrightarrow } \newcommand{\cat}[1]{ \mathcal{#1} } \newcommand{\u}[1]{ \underline{#1} } \newcommand{\bm}[1]{ \boldsymbol{#1} } \newcommand{\I}{\mathrm{I}} \newcommand{\A}{\wedge } % \newcommand{\EvL}{ (\!| } \newcommand{\EvR}{ |\!) } \newcommand{\sglt}{\bar{\boldsymbol{\sigma}} } % singlet % \require{color} \newcommand{\NUM}[1]{\textcolor{red}{( #1 )}\; } % \newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }% \newcommand{\For}{\Keyword{For } }% \newcommand{\Define}{\Keyword{Define } }% \newcommand{\Holds}{\Keyword{Holds } }%$

内容：

後知恵から言うと
セットアップと記法
余モナドのパンツマジック等式の記述
なぜパンツマジックなのか
典型的パンツマジック等式の証明
特殊な場合のパンツマジック等式
シングレット
おわりに

最初の記事（シリーズ目次あり）：準マルコフ圏からなる2-圏
次の記事：？？
前の記事：モノイド圏：評価写像の双関手性

後知恵から言うと

この記事のパンツマジック等式は、モノイド圏上の反ラックス・モノイド余モナド $\bm{F}/\cat{C}$ の余クライスリ圏 ${_\bm{F}\cat{C}}$ のなかで考えると次の等式に相当します。

$\quad \id_X ; \id_X = \id_X$

これは当たり前。

この記事のシングレットという概念は、 $X = t\EvL \vec{A} \EvR$ とした恒等射 $\id_X:X \to X \In {_\bm{F}\cat{C}}$ の $\cat{C}$ における表示です。また、シングレット＝クライスリ恒等射は、次の可換図式の縦方向の辺で与えられます。

$\require{AMScd} \begin{CD} F(t\EvL \vec{A} \EvR) @>{F(\beta\EvL \vec{A} \EvR)}>> F(t'\EvL \vec{A} \EvR) \\ @V{\gcoM_{t, \vec{A}} }VV @VV{\gcoM_{t', \vec{A}} }V\\ t\EvL F\oast\vec{A}\EvR @>{\beta \EvL F\oast \vec{A} \EvR}>> t'\EvL F\oast \vec{A} \EvR\\ @V{t\EvL \coU_{\oast \vec{A}} \EvR}VV @VV{t'\EvL \coU_{\oast \vec{A}} \EvR}V\\ t\EvL \vec{A} \EvR @>{\beta \EvL \vec{A} \EvR}>> t'\EvL \vec{A} \EvR \end{CD}$

と、このような事情を前もって知っていれば、この記事の書きっぷりはだいぶ変わっていたでしょう。もっとスッキリした展開になっていたはずです。が、発見的なガチャガチャした計算をそのまま残すのも一興かと思い、最初書いたストーリーを修正せずに記します。後知恵に基づく整理は別記事にします。

セットアップと記法

「反ラックス・モノイド余モナド：記号の使用・乱用再考」で述べた記法を使います。

$\cat{C}$ はモノイド圏で、 $F = (\u{F}, \delta, \varepsilon): \cat{C}\to \cat{C}$ は反ラックス・モノイド自己関手とします。そして、 $\bm{F} = (F, \coM, \coU)/\cat{C}$ を、 $F$ を台とする $\cat{C}$ 上の余モナドとします。余モナドの余乗法・余単位は反ラックス・モノイド自然変換です。それは以下が成立することです。

$\coM_{A\otimes B} ; (F(\delta_{A, B});\delta_{F(A), F(B)}) = \delta_{A, B} ; (\coM_A \otimes \coM_B)$
$\coM_{\I} ; (F(\varepsilon);\varepsilon) = \varepsilon$ （ $\I$ は単位対象）
$\coU_{A\otimes B} = \delta_{A, B}; (\coU_A \otimes \coU_B)$
$\coU_\I = \varepsilon$

余モナド $\bm{F}$ と、その台である反ラックス・モノイド関手 $F$ をオーバーロード（意図的に混同）はしません。が、反ラックス・モノイド関手 $F$ と台関手 $\u{F}:\u{\cat{C}} \to \u{\cat{C}}$ はオーバーロードします。つまり、反ラックス・モノイド関手の台関手を $F$ と書くことがあります。

$t\in |{\bf BUNTree}(n)|, \, \vec{f}:\vec{A} \to \vec{B}\In |\u{\cat{C}}|^n$ に対して、「モノイド圏：評価写像の双関手性」で導入した評価写像〈evaluation map〉の略記を使います。

$t\EvL \vec{A}\EvR := \Ev(t, A) \in |\u{\cat{C}}|^n$
$t\EvL \vec{f}\EvR := \Ev(t, \vec{f}) : t\EvL \vec{A}\EvR \to t\EvL \vec{B}\EvR \In \u{\cat{C}}$

モノイド圏とは限らない圏の一般的な話として、 $G:\cat{D} \to \cat{E}$ が関手（単なる関手）で、 $\vec{B} \in |\cat{D}|^n$ のとき、次の記法を使います。

$\quad G\oast \vec{B} = G \oast (B_1, \cdots, B_n) := (G(B_1), \cdots G(B_n)) \in |\cat{E}|^n$

' $\oast$ ' は、関手版fmapの中置演算子記号です。「反ラックス・モノイド関手の一般余結合律」で既に使っています。

同様な記法を自然変換に対しても使います。 $\varphi:: G \twoTo H:\cat{D}\to\cat{E}$ が自然変換、 $\vec{B} \in |\cat{D}|^n$ のとき：

$\quad \varphi_{\oast \vec{B}} = \varphi_{\oast (B_1, \cdots, B_n)} := (\varphi_{B_1}, \cdots, \varphi_{B_n}): G\oast \vec{B} \to H\oast\vec{B} \In \cat{E}^n$

対象／射、関手／自然変換の記述のために、「準マルコフ余モナドの計算と記述の方法」で紹介した行列形式記法を使います。ただし、対象と射が区別しやすいように、射には矢印を添える記法を使います。例えば、 $\xymatrix@1 { {A}\ar[r]^f & {B}\ar[r]^g & {C} }$ の書き方ならば：

以前の記法
$\begin{bmatrix} A \\ f \\ B \\ g \\ C\\ \end{bmatrix}$

新しい記法
$\begin{bmatrix} A \\ f \Arr \\ B \\ g \Arr \\ C\\ \end{bmatrix}$

余モナドのパンツマジック等式の記述

前節のセットアップと記法に従い、余モナドのパンツマジック等式を記述します。次は前もって決まって固定されているとします。

$\bm{F} = (F, \coM, \coU)/\cat{C}$ ：モノイド圏 $\cat{C}$ 上の反ラックス・モノイド余モナド
$F = \u{F} :\u{\cat{C}} \to \u{\cat{C}}$ ：台関手（記号の乱用）

$\gcoM_{t, \vec{A}}$ は、「反ラックス・モノイド関手の一般余結合律」で定義した一般余乗法〈generic comulitplication〉です。これは、反ラックス・モノイド関手 $F$ から決まるので $\gcoM^F_{t, \vec{A}}$ のように書くべきですが、反ラックス・モノイド関手は事前に決まっているので省略します。

余モナドのパンツマジック等式〈pants magic equation〉は次の主張です。

$\For n\in {\bf N} \\ \For t\in |{\bf BUNTree}(n)| \\ \For \vec{A} \in |\u{\cat{C}}|^n \\ \Holds \\ % \begin{bmatrix} F(t\EvL\vec{A}\EvR) \\ \coM_{t\EvL\vec{A}\EvR} \Arr\\ F( F(t\EvL\vec{A}\EvR) )\\ F(\gcoM_{t, \vec{A}} )\Arr\\ F(t\EvL F\oast \vec{A}\EvR )\\ F(t\EvL\coU_{\oast \vec{A} } \EvR )\Arr\\ F(t\EvL\vec{A}\EvR )\\ \gcoM_{t, \vec{A}} \Arr\\ t\EvL F\oast \vec{A}\EvR \\ t\EvL\coU_{\oast \vec{A}} \EvR \Arr\\ t\EvL\vec{A}\EvR \\ \end{bmatrix} = \begin{bmatrix} F(t\EvL\vec{A} \EvR) \\ \gcoM_{t, \vec{A}} \Arr\\ t \EvL F\oast \vec{A}\EvR\\ t \EvL \coU_{\oast \vec{A} }\EvR \Arr\\ t \EvL \vec{A}\EvR\\ \end{bmatrix}$

BUNツリー $t$ を変えると、見た目は違った様々な等式が得られます。

なぜパンツマジックなのか

余モナドのパンツマジック等式を、 $n = 2,\, t =(-\A -), \,\vec{A} = (A, B)$ の場合に考えてみます。記述は次のようになります。

$\begin{bmatrix} F( A\otimes B) \\ \coM_{A\otimes B} \Arr\\ F( F( A\otimes B) )\\ F(\delta_{A, B} )\Arr\\ F( F(A) \otimes F(B) )\\ F(\coU_{A} \otimes \coU_{B} )\Arr\\ F( A\otimes B )\\ \delta_{A, B} \Arr\\ F(A) \otimes F(B) \\ \coU_{A} \otimes \coU_{B} \Arr\\ A \otimes B \\ \end{bmatrix} = \begin{bmatrix} F( A\otimes B ) \\ \delta_{A, B} \Arr\\ F(A) \otimes F(B)\\ \coU_{A} \otimes \coU_{B} \Arr\\ A \otimes B \\ \end{bmatrix}$

等式の左辺のレイアウトを変えてみます（内容・意味は変わりません）。赤字の番号を追加しています。

$\begin{array}{c} \begin{bmatrix} F( A\otimes B) \\ \NUM{1}\coM_{A\otimes B} \Arr\\ F(F( A\otimes B)) \end{bmatrix}\\ F \begin{bmatrix} &F( A\otimes B)&\\ &\NUM{2}\delta_{A, B} \Arr&\\ F(A) &|& F(B) \\ \NUM{3}\coU_{A}\Arr &|& \NUM{4}\coU_{B}\Arr \\ A &|& B \\ \end{bmatrix}\\ \begin{bmatrix} &F(A \otimes B)& \\ &\NUM{5}\delta_{A, B} \Arr&\\ F(A) &|& F(B) \\ \NUM{6}\coU_{A}\Arr &|& \NUM{7}\coU_{B}\Arr\\ A &|& B \\ \end{bmatrix} \end{array}$

これをストライプ図に描けば次のようになります。

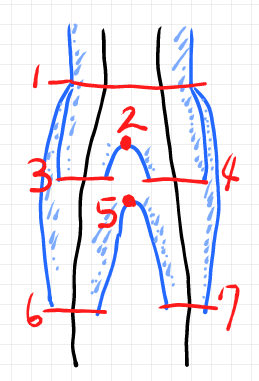
これが、下着の上にズボンを履いている姿に見えるだろう、ということです。ただし、下着は、レスリングのウェアのように上半身から繋がっていると考えてください（下の写真）。レスリングウェアはシングレット〈singlet〉と呼ぶんだそうです。ズボンも、股上が長いサルエルパンツ〈saruel pants〉を想定してください（その下の写真）。

赤で描いてあるのは、いずれも自然変換の成分である射です。これらはストリング図のノードですが横線で描いています。2番、5番は視認性の都合で“代表点”を描いていますが、これも自然変換の成分です。シングレット＆ズボンの比喩から次のように呼ぶことにします。

ベルト：余モナドの余乗法 $\coM_{A\otimes B}:F(A\otimes B) \to F(F(A\otimes B))$
シングレットの股：反ラックス・モノイド関手の余乗法 $\delta_{A ,B}:F(A\otimes B) \to F(A)\otimes F(B)$
シングレットの左裾：余モナドの余単位 $\coU_{A}: F(A) \to A$
シングレットの右裾：余モナドの余単位 $\coU_{B}: F(B) \to B$
ズボンの股：反ラックス・モノイド関手の余乗法 $\delta_{A, B}: F(A\otimes B) \to F(A)\otimes F(B)$
ズボンの左裾：余モナドの余単位 $\coU_{A}: F(A) \to A$
ズボンの右裾：余モナドの余単位 $\coU_{B}: F(B) \to B$

さて、等式の右辺をストライプ図で描くと次のようです。

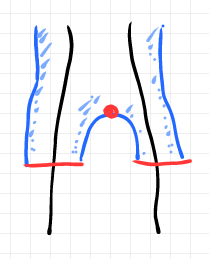
シングレットだけが残りベルトやズボンが消えています。マジックです。もちろんこの言い回しは比喩的なコジツケなので、あまり真に受けないでくださいね。

[補足]ストライプ図が表しているものは、人体のように3次元ソリッドなものではありません。ペランペランのシートが糊付けされているような図形を描いています。糊付けされたシートを置く場所として3次元空間を想定しているだけです。次の記事を参照してください。

[/補足]

典型的パンツマジック等式の証明

前節で出した $t = (-\A -)$ に対するパンツマジック等式を証明しましょう。

余モナド $\bm{F}/\cat{C}$ の余乗法や余単位は、反ラックス・モノイド自然変換なので、反ラックス・モノイド関手の余乗法と協調します。これは、余モナドの余乗法・余単位の位置と反ラックス・モノイド関手の余乗法の位置を入れ替え可能なことを意味します（「セットアップと記法」の冒頭参照）。このことを利用してパンツマジック等式を示します。

やり方は2通りあります。ひとつは、1番のベルトと3番・4番のシングレットの裾を、5番のズボンの股より下まで下げてしまうやり方。もうひとつは、3番・4番のシングレットの裾を2番のシングレットの股より上に上げるやり方です。

ここでは後者の方法で計算します。等式の左辺を再掲すると：

まずは3番・4番の移動。中段のブロックに次の等式を適用します。

$\NUM{2}\!\delta_{A, B}\;;\, (\NUM{3}\!\coU_A \,\otimes\, \NUM{4}\!\coU_B) = \NUM{3, 4}\!\coU_{A\otimes B}$

次のように変化します。

$\begin{array}{c} \begin{bmatrix} F( A\otimes B) \\ \NUM{1}\coM_{A\otimes B} \Arr\\ F(F( A\otimes B)) \end{bmatrix}\\ F \begin{bmatrix} &F( A\otimes B)&\\ &\NUM{3,4}\coU_{A\otimes B}\Arr & \\ &A\otimes B& \\ &\id_{A\otimes B} \Arr&\\ A &|& B \\ \end{bmatrix}\\ \begin{bmatrix} &F(A \otimes B)& \\ &\NUM{5}\delta_{A, B} \Arr&\\ F(A) &|& F(B) \\ \NUM{6}\coU_{A}\Arr &|& \NUM{7}\coU_{B}\Arr\\ A &|& B \\ \end{bmatrix} \end{array}$

上2つのブロックをまとめて簡略化します。

$\begin{array}{c} \begin{bmatrix} F( A\otimes B) \\ \NUM{1}\coM_{A\otimes B} \Arr\\ F(F( A\otimes B))\\ \NUM{3,4}F(\coU_{A\otimes B})\Arr \\ F(A\otimes B) \\ \end{bmatrix}\\ \begin{bmatrix} &F(A \otimes B)& \\ &\NUM{5}\delta_{A, B} \Arr&\\ F(A) &|& F(B) \\ \NUM{6}\coU_{A}\Arr &|& \NUM{7}\coU_{B}\Arr\\ A &|& B \\ \end{bmatrix} \end{array}$

上段のブロックは、余モナドの余単位律から $\id_{F(A\otimes B)}$ になるので、残るのは下段のブロックだけです。

$\begin{bmatrix} &F(A \otimes B)& \\ &\NUM{5}\delta_{A, B} \Arr&\\ F(A) &|& F(B) \\ \NUM{6}\coU_{A}\Arr &|& \NUM{7}\coU_{B}\Arr\\ A &|& B \\ \end{bmatrix}$

これで、目的の右辺が得られました。

赤字の番号を見ると、もともとあったズボンが残って、ベルトとシングレットのトランクス部分が消えたことになります。これは、マジックとしてはインパクトに欠けますね。別なやり方のほうでは、ベルトとズボンを膝下まで下げた後で、ベルトとズボンが消えます。この方法も確認してみてください。

単純さと汎用性からは、今述べた内側のシングレットの裾を上げる方法のほうが有利です。

特殊な場合のパンツマジック等式

前節で $t = (-\A -)$ の場合のパンツマジック等式を示しました。BUNツリーごとにパンツマジック等式の具体形があります。 $t = (\I -)$ と $t = \,!$ のときのパンツマジック等式もみておきましょう。BUNツリーを生成する基本記号とモノイド圏の単位対象がどちらも $\I$ なので注意してください。

まず、パンツマジック等式に出てくる反ラックス・モノイド関手の一般余乗法 $\gcoM_{t, \vec{A}}$ の特殊ケースを確認しておくと：

$\gcoM_{(\I -), (A)} = \id_{F(A)} : F((\I -)\EvL (A) \EvR) \to (\I -)\EvL F\oast (A) \EvR$
$\gcoM_{!, ()} = \varepsilon : F(!\EvL () \EvR) \to !\EvL F\oast () \EvR$

ここで次のような等式を使っています。

$(\I -)\EvL(A) \EvR = (A) = A$
$F\oast (A) = (F(A)) = F(A)$
$!\EvL() \EvR = \I$
$F\oast () = ()$
$F((\I -)\EvL (A) \EvR) = F(A)$
$(\I -)\EvL F\oast (A) \EvR = F(A)$
$F(!\EvL () \EvR) = F(\I)$
$!\EvL F\oast () \EvR = \I$

一般余乗法の特殊ケースとして恒等射や余単位も含まれていたわけです。

$t\EvL \coU_{\oast \vec{A}} \EvR$ の特殊ケースも確認しておくと：

$(\I - )\EvL \coU_{\oast (A)} \EvR = (\I - )\EvL \coU_{A} \EvR = \coU_{A}$
$!\EvL \coU_{\oast ()} \EvR = !\EvL () \EvR = \id_\I$

これらの値（対象や射）を、一般的パンツマジック等式に代入すると目的の具体形が得られます。

$t = (\I -)$ の場合：

$\begin{bmatrix} F( A ) \\ \coM_{ A } \Arr\\ F( F( A ))\\ F(\id_{F(A)} )\Arr\\ F( F(A) )\\ F( \coU_{A} )\Arr\\ F( A )\\ \id_{ F(A) } \Arr\\ F(A) \\ \coU_{A} \Arr\\ A \\ \end{bmatrix} = \begin{bmatrix} F( A ) \\ \id_{F(A)} \Arr\\ F(A)\\ \coU_{A} \Arr\\ A\\ \end{bmatrix}$

恒等射を取り除くと：

$\begin{bmatrix} F( A ) \\ \coM_{ A } \Arr\\ F( F( A ))\\ F( \coU_{A} )\Arr\\ F( A )\\ \coU_{A} \Arr\\ A \\ \end{bmatrix} = \begin{bmatrix} F( A ) \\ \coU_{A} \Arr\\ A\\ \end{bmatrix}$

これは確かに成立しています。

$t = !$ の場合：

$\begin{bmatrix} F( \I ) \\ \coM_\I \Arr\\ F( F( \I ) )\\ F( \varepsilon )\Arr\\ F( \I )\\ F( \id_\I )\Arr\\ F( \I )\\ \varepsilon \Arr\\ \I \\ \id_\I \Arr\\ \I \\ \end{bmatrix} = \begin{bmatrix} F( \I ) \\ \varepsilon \Arr\\ \I\\ \id_\I \Arr\\ \I \\ \end{bmatrix}$

恒等射を取り除くと：

$\begin{bmatrix} F( \I ) \\ \coM_\I \Arr\\ F( F( \I ) )\\ F( \varepsilon )\Arr\\ F( \I )\\ \varepsilon \Arr\\ \I \\ \end{bmatrix} = \begin{bmatrix} F( \I ) \\ \varepsilon \Arr\\ \I\\ \end{bmatrix}$

これも成立しています。

シングレット

例え話として「シングレット」（レスリングウェア）という言葉を出しました。「シングレット」を、反ラックス・モノイド余モナドに関連するテクニカルタームとして定義しましょう。

今まで同様、 $\bm{F}/\cat{C}$ は、モノイド圏 $\cat{C}$ 上の反ラックス・モノイド余モナドとします。シングレットは、BUNツリーと対象のリストに対して定義されます。次の記号でシングレットを表します。

$\quad {\sglt^\bm{F}}_{t, \vec{A}}$

反ラックス・モノイド余モナドは前もって決まっているので省略してかまいません。

シングレット〈singlet〉の定義は以下のようです。

$\For n\in {\bf N}\\ \For t \in |{\bf BUNTree}(n)|\\ \For \vec{A} \in |\u{\cat{C}}|^n \\ \Define \\ \quad \sglt_{t, \vec{A}} := \begin{bmatrix} F(t\EvL\vec{A} \EvR) \\ \gcoM_{t, \vec{A}} \Arr\\ t \EvL F\oast \vec{A}\EvR\\ t \EvL \coU_{\oast \vec{A} }\EvR \Arr\\ t \EvL \vec{A}\EvR\\ \end{bmatrix} = \gcoM_{t, \vec{A}}; t \EvL \coU_{\oast \vec{A} }\EvR$

シングレットを構成するために必要な素材は、余モナドから得られるので、余モナド $\bm{F}/\cat{C}$ が決まっている状況ではシングレットを定義できます。

シングレットを使えば、パンツマジック等式は簡略に書けます。

$\For n\in {\bf N}\\ \For t \in |{\bf BUNTree}(n)|\\ \For \vec{A} \in |\u{\cat{C}}|^n \\ \Holds \\ \quad \coM_{t\EvL \vec{A}\EvR};F(\sglt_{t,\vec{A}});\sglt_{t,\vec{A}} = \sglt_{t,\vec{A}}$

おわりに

前節で定義したシングレット ${\sglt^\bm{F}}_{t, \vec{A}}$ は、余クライスリ圏 ${_\bm{F}\cat{C}}$ の恒等射 $\id_{t\EvL \vec{A}\EvR}$ （の表示）のことです。「反ラックス・モノイド余モナドの余クライスリ圏その1」の記号の約束に従うと、余クライスリ圏の恒等射にはハットを付けるので、次のように書けるでしょう。

$\quad \widehat{\id}_{t\EvL \vec{A}\EvR} = \sglt_{t, \vec{A}}$

最初の節で述べたように、余クライスリ圏 ${_\bm{F}\cat{C}}$ では自明な等式を、もとのモノイド圏 $\cat{C}$ のなかでガチャガチャ計算していたわけです。 $\cat{C}$ のなかでのガチャガチャした計算が必要になることもあります。今回の話は、そんなときに参考になるかも知れません。

*1:元記事： http://seishikimeishou.blog.fc2.com/blog-entry-27.html
元画像： https://blog-imgs-110-origin.fc2.com/s/e/i/seishikimeishou/online_P4400_sub_model2.jpg

*2:元記事（商品）： https://www.amazon.co.jp/dp/B00ANXAF0E