このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

圏論的レンズ 最初の一歩： ストリング図を中心に

雑記／備忘

\newcommand{\Iff}{\Leftrightarrow } \newcommand{\id}{\mathrm{id} } \newcommand{\In}{\text{ in } } \require{color} \newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }% \newcommand{\For}{\Keyword{For } }% \newcommand{\Define}{\Keyword{Define } }% \newcommand{\Where}{\Keyword{Where } }% \newcommand{\Holds}{\Keyword{Holds } }% % \newcommand{\get}{\mathrm{get}} \newcommand{\put}{\mathrm{put}} \newcommand{\lid}{\mathrm{lid}} \newcommand{\req}{\mathrm{req}} \newcommand{\resp}{\mathrm{resp}} プログラミングにおいて、レンズ〈lens〉と呼ばれる構造が使われる機会が増えているようです。古典的なレンズが幾つかの方向に一般化されていて、「レンズってなに？」と聞かれても答えにくい状況になっています。

一番簡単な（と僕が思っている）ストレージの例からはじめて、具象レンズを導入し、それらのあいだの関係を調べます。記述と計算にストリング図を使用します。

内容：

シリーズ目次（リンク）：

  1. 圏論的レンズ 最初の一歩： ストリング図を中心に（この記事）
  2. 圏論的レンズ 2： 具象オプティック
  3. 圏論的レンズ 訂正と補足： 具象レンズ＝具象オプティック
  4. 圏論的レンズ 3： レンズ／オプティックのための描画法
  5. 圏論的レンズ 4： テレオロジー圏
  6. 圏論的レンズ 5： オプティック構成とテレオロジー圏
  7. 圏論的レンズ 6： 丹原／ペイストロ／ストリート随伴系

関連する記事：

  1. オプティック界隈の丸付き文字と記号の乱用

元祖レンズ

歴史的な経緯はまったく調べてないので、ほんとに“元祖”かどうかは定かでないのですが、便宜上、以下のように定義される構造を元祖レンズ〈original lens〉と呼ぶことにします。

レンズとは、get と put （または view と update）と呼ばれる2つの関数の組である。

\quad \get :A \to B\\ \quad \put :A\times B \to A

レンズの入門には、たいてい上のように書いてあります。集合 A はファイルやデータベースのようなストレージ（の状態の型）を表し、集合 B は何らかの値（の型）を表すと考えましょう。get は値の取得、put はストレージの更新ですね。

ストレージだと考えると、get/put は何らかの法則に従うだろうと予想できます。実際、次のような法則があります。

  1. put-get 法則：\forall x\in A, y\in B.\, \get(\put(x,y)) = y
  2. get-put 法則：\forall x\in A, y\in B.\, \put (x, \get (x)) = x
  3. put-put 法則：\forall x\in A, y, y'\in B.\, \put(\put(x, y), y') = \put(x, y')

これらの法則を満たすレンズは有法則レンズ〈lawful lens〉と呼びます。最初の2つの法則を満たすレンズを良振る舞いレンズ〈well-behaved lenses〉、3つの法則全部を満たすレンズを最良振る舞いレンズ〈very well-behaved lenses〉と呼ぶこともあります*1。

一方、何の法則も考えずに get と put の組だけ考えているときは無法則レンズ〈lawless lens〉と呼びます。

無法則レンズのほうが簡単なので、無法則レンズをベースに一般化して、必要に応じて法則性を入れるというアプローチが普通のようです。

実際のストレージのモデルとしては有法則レンズが適切ですが、ここでは法則性は無視した無法則レンズを考えます。そのほうが簡単ですからね。なので、以下単にレンズと言ったら、それは無法則レンズのことです。

元祖レンズの圏

元祖レンズ（無法則レンズなので get と put の組）は結合〈合成 | compose〉することができます。この結合演算によって、元祖レンズは全体として圏を形成します。

圏の記法と合うように、ひとつの元祖レンズを f:A \to B 、もうひとつの元祖レンズを g:B \to C のように書きます。もう少し詳しく書くと：

\quad f = (f_\get, f_\put) : A \to B \In {\bf OrgLens}\\ :\Iff f_\get:A \to B, f_\put:A\times B \to A \In {\bf Set}\\ \:\\ \quad g = (g_\get, g_\put) : B \to C \In {\bf OrgLens}\\ :\Iff g_\get:B \to C, g_\put:B\times C \to B \In {\bf Set}

説明：

  • 元祖レンズ f のgetパートを f_\get、putパートを f_\put と書く。
  • 元祖レンズ f のgetパートは、f_\get:A \to B という集合圏の射、つまり写像。
  • 元祖レンズ f のputパートは、f_\put:A\times B \to A という集合圏の射、つまり写像。
  • 元祖レンズの圏 {\bf OrgLens} において、元祖レンズ f のプロファイル（域と余域）は A \to B 、つまり、見かけ上はgetパートと同じプロファイル。
  • g に関しても同様。

念の為に、圏 {\bf OrgLens} の対象類とホムセットを定義しておきます。

  • |{\bf OrgLens}| := |{\bf Set}|
  • {\bf OrgLens}(A, B) := {\bf Set}(A, B)\times {\bf Set}(A\times B, A)

圏になるためには、射の結合と恒等射が必要です。それは以下のように定義します。定義において、集合圏 {\bf Set} の結合／恒等と区別するために、元祖レンズの圏 {\bf OrgLens} の結合／恒等は記号 ';;',\; '\lid' を使います。

\For f:A \to B, g:B \to C \In {\bf OrgLens}\\ \Define f;;g := (f_\get;g_\get, \big( (\Delta_A ; (\id_A \times g_\get))\times \id_C \big) ; (\id_A \times g_\put) ; f_\put)

\For A \in |{\bf OrgLens}|\\ \Define \lid_A := (\id_A, \pi^2_{A, A})

ここで、\Delta は集合圏の対角射、\pi^2 は集合圏の第ニ射影です。

この定義で、元祖レンズの結合 f;;g のputバートが複雑に見えて鬼門かも知れません。ストリング図を描いてみましょう。結合の方向が上から下、直積の方向が左から右です。

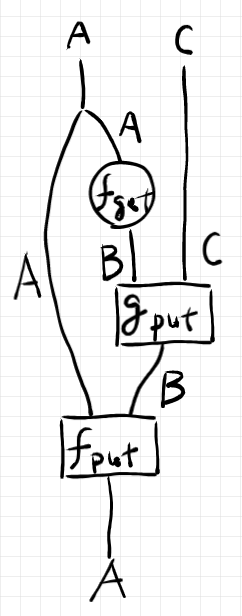
この図を見ながらゆっくりと考えてみましょう。

結合 f;;g のputバート〈updateパート〉がやるべきことは、A のストレージ状態を、C の値を使って更新することです。そのためにまず、A から f_\get を使って B の値を取り出します。取り出した B の値は A の状態の一部であり再びストレージ状態とみなせるとします。

取り出した結果である B の状態は C の値で更新できますから、g_\put を使って更新しましょう。そしてさらに、更新済みの B の状態（値ともみなせる）をもとの A に反映させる必要があります。それには、f_\put を使えばいいのです。

以上の手順が (f;g)_\put の定義を与えます。A のストレージ状態は f_\get の入力としても f_\put の入力としても使われるのでコピーする必要があります。コピーには対角射 \Delta_A （図ではワイヤーの分岐）が使われます。

ストレージ状態をgetパートを使って値として取り出すのですが、取り出した値がまたストレージ状態とみなせるところがキモです。

元祖レンズ達はホントに圏なのか？

前節で、圏 {\bf OrgLens} の対象類、ホムセット、結合、恒等が定義できました。素材はちゃんと揃っています。しかし、圏であるためには、圏としての法則を満たす必要があります。それら“圏の法則”は次のものです。

\For f:A \to B, g:B \to C, h:C \to D \In {\bf OrgLens}\\ \Holds (f;;g);;h = f;;(g;;h)\\ \:\\ \For f:A \to B\In {\bf OrgLens}\\ \Holds \lid_A;;f= f\\ \Holds f;;\lid_B= f

これらの法則が成立するかどうかは、射（元祖レンズ）のgetパートとputパートをそれぞれ見ていけばいいのですが、一番面倒そうなのは、結合律〈associative law〉のputパートでしょう。そこだけ書き出してみます。

\quad \big( (f;;g);;h\big)_\put = \big(f;;(g;;h)\big)_\put

これを示すにも、ストリング図を使うのが便利です。たまたま今週、ストリング図の記事を書いたので、そこで紹介した描画法を使います。

getパートは丸、putパートは四角で、f, g, h はそれぞれ塗りパターン「ベタ塗り、斜線網掛け、砂目網掛け」で区別します。ワイヤーへのラベリングはほとんど省略します。

示すべき等式を絵に描くと次のようになります。

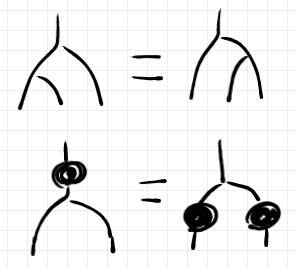
上記の等式を示すために本質的に必要なことは次の等式です。

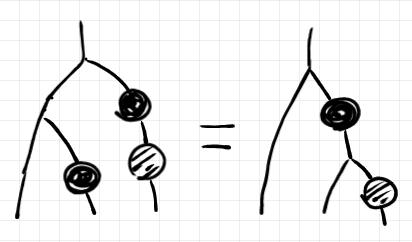
この等式は、対角射〈コピー射〉の余結合律と、対角射に沿って射もコピーされること*2から出ます（下図参照）。

恒等射の単位律はもっと簡単に証明できます。

Webサーバーモデル

前節の元祖レンズの説明では3種の記述方法を使いました。

  1. ストレージ（ファイルやデータベースのようなデータ格納媒体）を引き合いに出した比喩的説明。「元祖レンズはストレージだと考えよう」はメンタルモデル（心にいだくイメージ）の話です。
  2. 集合圏（対象は集合、射は写像）における形式的な定義。
  3. ストリング図を使った視覚的表現。

これから元祖レンズを少し一般化した具象レンズ〈concrete lens〉を導入するのですが、圏論を使った形式的定義にはちょっと準備が必要なのでそれは省略します。が、ストリング図を使った表現は紹介します。まず最初はメンタルモデルの話 -- Webサーバーの話から始めます。

Webの通信に使われているHTTPプロトコルでは、リクエストとレスポンスの区別があります。インターネットと向き合っているフロントのサーバーがリクエストを受け取り、それをバックエンド（アップストリーム）に中継するとしましょう。このとき、HTTPリクエスト・データを加工してバックエンドに対するリクエストを作ります。また、バックエンドから戻ってきたレスポンス・データも加工してインターネットに送り出すとします。

HTTPリクエストのデータ型を A、バックエンドへのリクエストのデータ型を B、バックエンドからのレスポンスのデータ型を Y、HTTPレスポンスのデータ型を X とすると、次のような絵が描けます。

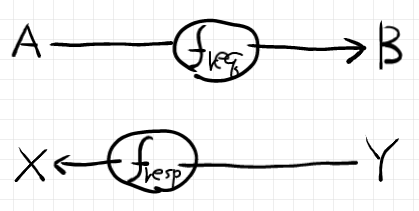
上段のリクエストは左から右に向かい、下段のレスポンスは右から左に向かいます。f_\req はリクエストを加工する関数、f_\resp はレスポンスを加工する関数です。

バックエンドからのレスポンスを加工するとき、もとのHTTPリクエストのデータも必要なときがあります。そんなときは、元リクエストを一時的に保存しておいて、戻り（バックエンドからのレスポンス）を加工するときに使用します。そんな状況を絵に描くと次のようになります。

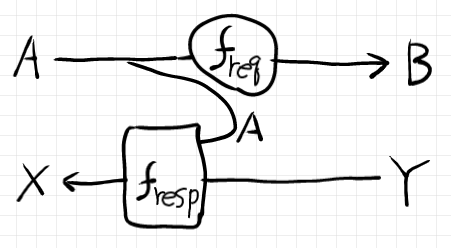
この絵で表されるリクエスト処理／レスポンス処理を一塊〈ひとかたまり〉にして、Webサーバー処理のコンポネント（機能的単位）と考えましょう。コンポネントは、2つの写像〈関数〉f_\req, f_\resp の組で決まります。それぞれの写像のプロファイルを書けば：

\quad f_\req : A \to B \In {\bf Set}\\ \quad f_\resp : A\times Y \to X \In {\bf Set}

このコンポネントは、多段階に繋ぐことができます。f = (f_\req, f_\resp) と g = (g_\req, g_\resp) を繋いだ絵は次のようになります。ここでは、f はベタ塗り、g は斜線網掛けで描いています。

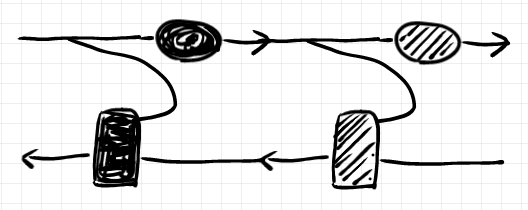
繋いだ複合コンポネントを f;;g と書くことにすると、演算 ;; が圏の結合になることは（直感的には）明らかでしょう。次のようなコンポネントが恒等射になります。

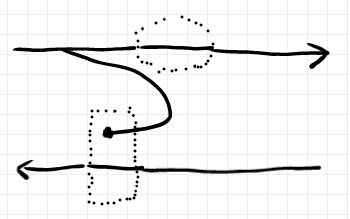
点線の丸は恒等射 \id_A を表し、点線の四角は第二射影 \pi^2_{A, X} を表します。

具象レンズ

前節でインフォーマルに導入された“コンポネント”が具象レンズ〈concrete lens〉*3です。Webサーバー・コンポネントの例え話はともかくとしして、ストリング図による記述は十分に正確です。正確なんですが、その解釈には若干高度な圏論的道具が必要になるのです。

元祖レンズのメンタルモデルであるストレージと、具象レンズのメンタルモデルであるWebサーバー・コンポネントはだいぶ違いがありますが、実は、抽象的レベルでは同じ概念になります（次節で述べる）。ただし、具象レンズのほうが少しだけ一般化しています。

具象レンズを構成する関数を再掲すると：

\quad f_\req : A \to B \In {\bf Set}\\ \quad f_\resp : A\times Y \to X \In {\bf Set}

一方、元祖レンズを構成する関数は：

\quad f_\get : A \to B \In {\bf Set}\\ \quad f_\put : A\times B \to A \In {\bf Set}

そうです； 具象レンズにおいて X = A, Y = B と置けば元祖レンズになります。

元祖レンズの圏の対象は単一の集合でしたが、具象レンズの圏では対象が集合のペアになります。具象レンズ f のプロファイルは次のように書けます。{\bf ConcLens} は具象レンズの圏です。

\quad f = (f_\req, f_\resp): (A, X) \to (B, Y) \In {\bf ConcLens}\\ \Where\\ \quad f_\req : A \to B \In {\bf Set}\\ \quad f_\resp : A \times Y \to X \In {\bf Set}

具象レンズのリクエストパート f_\req、レスポンスパート f_\resp は例え話に由来する記法で、具象レンズの記述には次の記法が多く用いられます。

\quad f = (f, f^\#) : (A, X) \to (B, Y) \In {\bf ConcLens}

これは記号の乱用で、紛らわしくて僕は嫌いです。ここでは、以下の記法にします。

\quad f = (f_\#, f^\#) : (A, X) \to (B, Y) \In {\bf ConcLens}

具象レンズ f の向きは f_\# の向きと同じなので、f_\# を順行パート〈forward part〉、逆向きになる f^\# を逆行パート〈backward part〉と呼びます。具象レンズは互いに逆方向な2つのパートを持ちます。

元祖レンズでは、順行パートをgetパート、逆行パートをputパートと呼んでいたわけです。

元祖レンズと具象レンズ

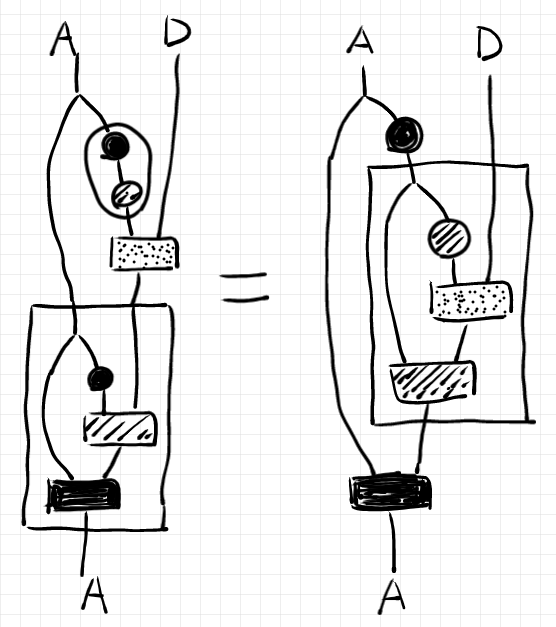
元祖レンズと具象レンズでは、例え話に使った素材（ストレージとWebサーバー・コンポネント）も違うし、ストリング図の見た感じも随分と違います。しかし、これらは同じ概念なのです。そのことをストリング図の変形で示してみます。

Webサーバー・コンポネントをモデルにした具象レンズのストリング図から、ストレージをモデルとした元祖レンズのストリング図へと変形します。変形に使う法則は、既に出た次の法則です。

次の絵からスタートします。2つの具象レンズを結合した絵です。

黒丸のノードを分岐を超えて左に移動します。コピーされて2つの黒丸ノードになります。

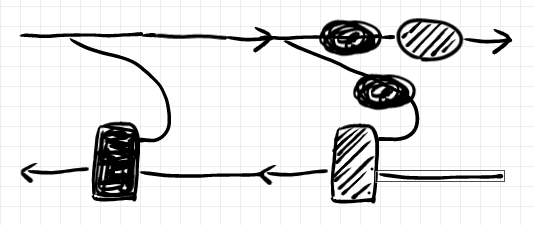
対角射〈コピー射〉の余結合律により、ワイヤーを繋ぎ替えます。

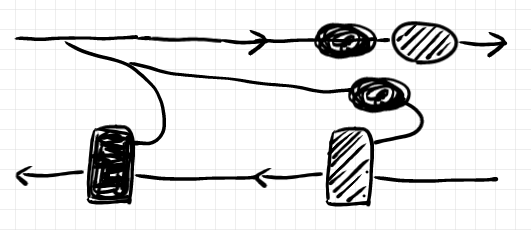
レイアウトを変更します。

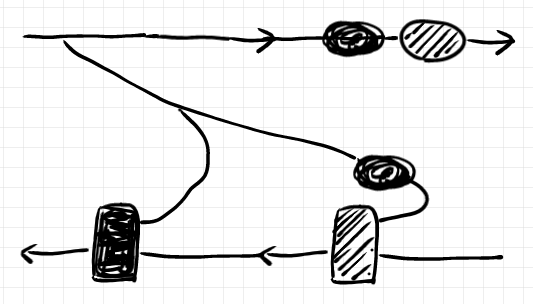
さらにレイアウトを変更します。

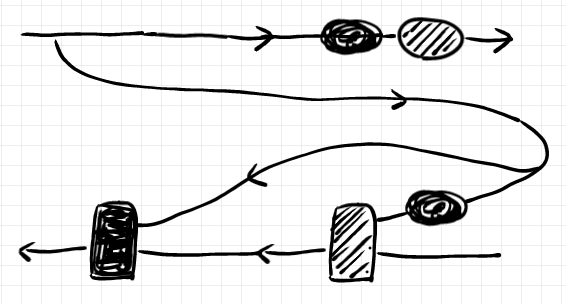
下の図の丸で囲った部分と四角で囲った部分に注目してください。それぞれ、元祖レンズのgetパートの結合、putパートの結合と同じです*4。

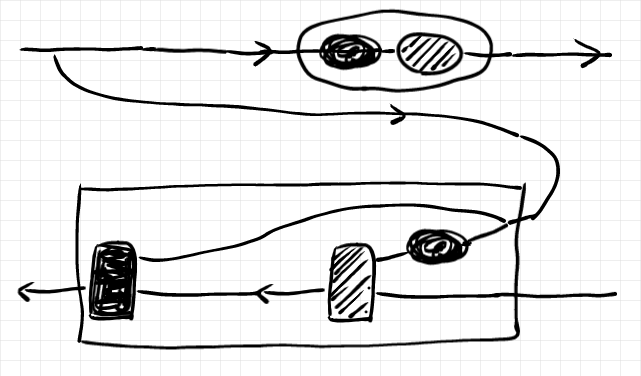
Webサーバー・コンポネントの結合と、ストレージのget/putの結合は一見違うように見えますが、実質的には同じなのです。

おわりに

具象レンズは（元祖レンズも）順行パートと逆行パートの2つの写像のペアになっています。互いに逆方向の写像を組み合わせることにより、双方向のデータ処理や双方向の情報通信のモデルとなっているわけです。

冒頭でも述べたように、元祖レンズ／具象レンズから様々な一般化がされていて、ナントカ・レンズが矢鱈にあります。一般化のために、けっこうヘビーな圏論的道具立て（グロタンディーク構成、アクテゴリー、コエンド計算、パラ構成など）が使われたりもします。

ですが、アブストラクト・ナンセンスに飛び込む前に、元祖レンズ／具象レンズとそのストリング図をいじっておいたほうがよいかと思います。

*1:スタックのpop/pushをget/putだと思うと、良振る舞いレンズですが最良振る舞いレンズにはなりません。

*2:準マルコフ圏の文脈では、この性質を僕は射の非分散性〈nondispersiveness〉と呼んでいます。デカルト圏ではすべての射が非分散的です。

*3:具象という形容詞を付けているのは、もっと抽象的なレンズ概念が色々とあることを示唆します。

*4:図の向きが変わることで混乱してしまう人は「双対や随伴に強くなるためのトレーニング」のトレーニングをしましょう。