圏論的レンズ訂正と補足：具象レンズ＝具象オプティック - 檜山正幸のキマイラ飼育記 (はてなBlog)

$\newcommand{\id}{\mathrm{id} } \newcommand{\In}{\text{ in } } % \newcommand{\get}{\mathrm{get}} \newcommand{\put}{\mathrm{put}}$ 「圏論的レンズ 2：具象オプティック」において、次のように書きました。

具象オプティックを定義すると、具象レンズは特殊な具象オプティックとみなせます。「圏論的レンズ最初の一歩：ストリング図を中心に」において、具象レンズの圏 ${\bf ConcLens}$ の形式的定義は省略しましたが、具象オプティックの圏 ${\bf ConcOptic}$ をちゃんと定義すれば、具象レンズの圏はその部分圏として確定します； ${\bf ConcLens} \subseteq {\bf ConcOptic}$ 。

この記述は、未確認の状況に対する僕の誤認に基づいていました。

${\bf ConcLens} \subseteq {\bf ConcOptic}$ ではなくて、実際は ${\bf ConcLens} = {\bf ConcOptic}$ となります。「2つの圏が同じ圏なら部分圏と言えるので論理的に間違ったことは言ってない」と強弁もできますが、同じ圏だと思ってなかったという点で完全に勘違いしてました。

内容：

表示が異なっても同じ同値類
具象オプティックに対する2つの表示法
具象オプティック表示から具象レンズ表示へ
まとめ

最初の記事＋シリーズ目次

表示が異なっても同じ同値類

「圏論的レンズ 2：具象オプティック」で次のようなことも書きました。

具象オプティックは具象オプティック実装の同値類として定義されました。これは、有理数が分数の同値類として定義されているのと事情は同じです。

具象オプティック：具象オプティック実装＝有理数：分数

一般に、 $Q = X/\!\sim$ のとき、 $X$ の要素を $Q$ の要素の表示〈presentation〉とも呼びます。この言葉を使うと、具象オプティック実装は具象オプティックの表示となります。

これからレンズ／オプティックについて話すことを、分数と有理数で例えてみます。分数の分母に負の整数も許すとします。例えば、 $\frac{2}{-4}$ 。ひとつの有理数に対して、その表示である分数はたくさんあります。例えば、次はいずれも有理数 $- \frac{1}{2}$ *1の表示です。

$\quad \frac{2}{-4},\, \frac{-2}{4},\, \frac{3}{-6},\, \frac{-3}{6}$

分数として、分母が正のものだけ考えても有理数を表現できます。表示の集合は違っても、商集合は同じになります。次のようなことです。

分数の集合： ${\bf Z} \times {\bf Z}_{\ne 0}$
分母が正の分数の集合： ${\bf Z} \times {\bf Z}_{\gt 0}$
商集合は同じ： $({\bf Z} \times {\bf Z}_{\ne 0})/\!\sim\; = ({\bf Z} \times {\bf Z}_{\gt 0} )/\!\sim\; = {\bf Q}$

このことは、任意の分数（分母が負でもよい）に対して、同じ有理数を表す“分母が正の分数”を作れば示せます。

先に引用した文言で：

具象レンズは特殊な具象オプティックとみなせます。

これは不正確で、正しくは：

“具象レンズの表示”は、特殊な（制限した）“具象オプティックの表示”とみなせます。

表示〈実装〉としては違うけど、表す実体〈同値類〉は同じでした。勘違いしてました。ごめんなさい。

具象オプティックに対する2つの表示法

具象オプティックを $\langle f_\# \mid f^\#\rangle$ と書きましたが、 $(f_\# , f^\#)$ が表示〈具象オプティック実装〉です。

$(f_\#, f^\#) \in {\bf Set}(A, R\times B) \times {\bf Set}(R\times Y, X) \:\text{ for some }R$
$\pi : {\bf Set}(A, R\times B) \times {\bf Set}(R\times Y, X) \to {\bf ConcOptic}( (A, X), (B, Y))$ （規準的射影）
$\pi( (f_\#, f^\#) ) = \langle f_\# \mid f^\#\rangle$
$\langle f_\# \mid f^\#\rangle \in {\bf ConcOptic}( (A, X), (B, Y))$

具象オプティック実装の順行パート $f_\#$ と逆行パート $f^\#$ は対称性がありますが、それは表示の対称性です。対称性がない表示が対称性のある表示と同じ実体〈同値類〉を表すことはあるかも知れません。

対称性がない表示とは、具象レンズのgetパートとputパートによる表示です。getパートとputパートによる具象オプティックの表示を $\langle h_\get \vdash h_\put \rangle$ と書くことにします。

$(h_\get, h_\put) \in {\bf Set}(A, B) \times {\bf Set}(A\times Y, X)$
$\pi' : {\bf Set}(A, B) \times {\bf Set}(A\times Y, X) \to {\bf ConcOptic}( (A, X), (B, Y))$ （規準的射影）
$\pi'( (h_\put, h_\get) ) = \langle h_\get \vdash h_\put \rangle$
$\langle h_\get \vdash h_\put \rangle \in {\bf ConcOptic}( (A, X), (B, Y))$

具象レンズ表示（getパートとputパートによる表示）を具象オプティック表示（順行パートと逆行パートによる表示）に書き換えるのは容易で、次の等式が成立します。

$\quad \langle h_\get \vdash h_\put \rangle = \langle \Delta_A; (\id_A\times h_\get) \mid h_\put \rangle : (A, X)\to(B, Y) \In {\bf ConcOptic}$

問題は逆の書き換えで、与えられた具象オプティック表示 $( f_\# , f^\#)$ から同値な（同じ同値類を表す）具象レンズ表示 $( h_\get , h_\put )$ を作れるか？です。

具象オプティック表示から具象レンズ表示へ

一般的に、写像 $f:A \to R\times B$ に対して次が成立します。

$\quad f = \Delta_A;( (f;\pi_{R, B}^1) \times (f;\pi_{R, B}^2)) \In {\bf Set}$

ここで、 $\Delta_A$ は対角射、 $\pi_{R, B}^1,\, \pi_{R, B}^2$ は直積 $R\times B$ の第一射影、第二射影です。これらの射影は次のように書けます。

$\quad \pi_{R, B}^1 = (\id_R \times !_B);\rho_R : R\times B \to R \In {\bf Set}\\ \quad \pi_{R, B}^2 = (!_R \times \id_B );\lambda_B : R\times B \to B \In {\bf Set}$

ここで、 $!_B,\, !_R$ は終対象（特定された単元集合）への唯一の写像、 $\rho_R, \, \lambda_B$ は右単位律子、左単位律子です。

以上の状況をストリング図に描きましょう。結合の方向が上から下、直積の方向を左から右とします。この描画方向だと、 $\Delta,\, !$ が象形文字として解釈できます。

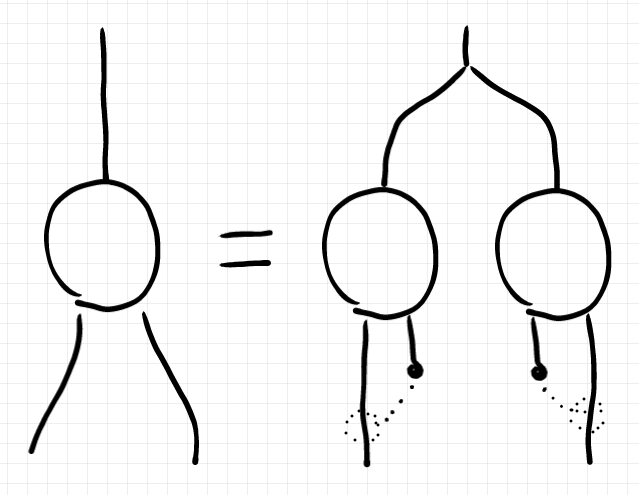
点線で描いた右単位律子、左単位律子は通常は省略します。

さて、以下の絵は、具象オプティックのオプティック表示 $(f_\#, f^\#)$ だとします。ここでは、絵〈ストリング図〉は同値類を取る前の表示〈実装〉そのものだとみなします。

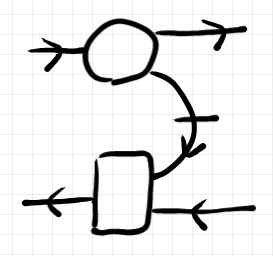
具象オプティック表示 $(f_\#, f^\#)$ の順行パート $f_\#$ （丸）を上に述べた方法で分解します。

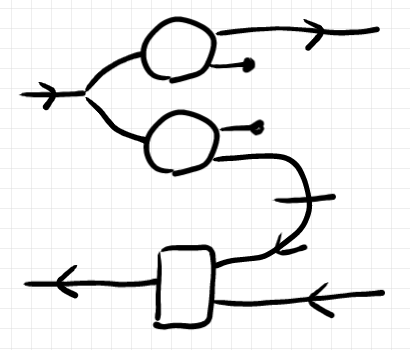
$f_\#; \pi^1$ をエンコーダーとみなして、曲がった残余ワイヤーに沿って逆行パート側にスライドします。移動後に $f_\#; \pi^1$ はデコーダーになります。

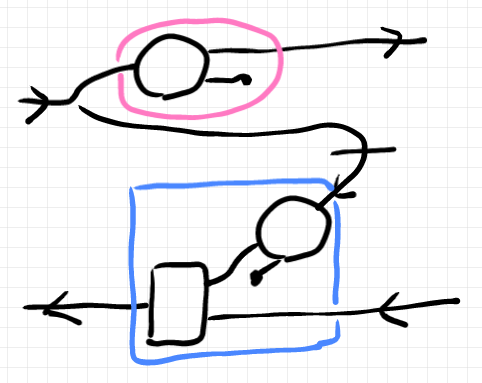
ピンクの丸をgetパート、水色の四角をputパートとすると、これは具象レンズ表示になります。

与えられた $( f_\# , f^\#)$ に対して、

$\quad \langle h_\get \vdash h_\put \rangle = \langle f_\# \mid f^\# \rangle$

となる具象レンズ表示のgetパート／putパートを具体的に書けば：

$\quad h_\get := f_\#;\pi^2_{R,B} : A \to B \In {\bf Set}\\ \quad h_\put := ( (f_\#;\pi^1_{R,B}) \times \id_Y);f^\# : A\times Y \to X \In {\bf Set}$

以上で、「具象レンズ表示 ←→ 具象オプティック表示」という同値な（同値類を変えない）変形ができることがわかりました。

まとめ

元祖レンズの圏 ${\bf OrgLens}$ と具象レンズの圏 ${\bf ConcLens}$ の圏は違う圏です。対象類が違います。 $A \mapsto (A, A)$ という対応を埋め込み関手に拡張すれば、

$\quad {\bf OrgLens} \subseteq {\bf ConcLens}$

とみなせます。

この記事で、具象レンズの圏 ${\bf ConcLens}$ と具象オプティックの圏 ${\bf ConcOptic}$ は同じであることを示しました。

$\quad {\bf ConcLens} = {\bf ConcOptic}$

定義は違うのですが、その違いはどのような表示を選ぶかでした。どちらの表示（具象レンズ表示、具象オプティック表示）を選んでも、同値類を取ってしまえば同じ実体になってしまいます。なので、実体（同値類）達により作られる圏は同じです。

では、具象オプティック圏の定義が無意味なのか？というと、そうではありません。具象レンズ表示と具象オプティック表示が同値であることは、集合圏（より一般にはデカルト圏）特有の事情に依存しています。一般的な圏では、レンズ表示とオプティック表示が同じであることは保証できません。オプティック表示のほうが一般性も対称性も高いのは事実です。

以上の理由から、より一般的・抽象的な“オプティックの圏”の構成・定義にはオプティック表示が使われます。

*1:「 $- \frac{1}{2}$ も表示ではないか」と言われればそうなんですけど、そこは察してください。