テキストの計算をほとんどしない(「ほとんどできない」とも言う)檜山が、絵算〈ストリング図計算〉のコツと小技を書いてみますよ。
似た趣旨の過去記事に次があります。
今回の記事は、一般的入門的解説ではなくて“コツと小技”です。
内容:
前置きと例題
人に見せることを考慮しないで、自分の作業としてストリング図を描き・操作する状況での話をします。ストリング図は、単色の鉛筆やボールペンで手描きすることを想定しています。事例では一部色を使ってますが、これは視認性向上のためで必須ではありません。
描画方向は、射の結合方向が上から下、モノイド積の方向が左から右です。射の結合方向は下から上が多数派な気がしますが、個人的な好みは上から下で、それを使ってます。描画方向は好みの問題なので、好きにしてください*1。描画方向の変更への対応能力を養う方法は以下の記事に書いています。
例題としては、「マルコフ圏が条件化可能〈conditionalizable〉なら反転可能〈convertible〉である」という命題を使います。ただし、この命題を証明する気はなくて、説明用の素材をこの例題から取るだけです。例題の内容を知りたいなら、次の記事が参考になるでしょう。
マルコフ圏に関する用語・記法は常識的なものを使いますが、単位対象兼終対象を と書きます。
名称と形状
絵算の良い所のひとつは、名称による識別の代わりに絵図記号〈ピクトグラム | アイコン〉の形状による識別が使えることです。名称には同義語がたくさんあってやんなっちゃうんですが、形状の意味を約束すれば、同義語の煩わしさから開放されます。
たくさんの名称を簡潔に表すために正規表現を使います。
- {‥}? 中括弧内は省略可能
- {‥ | ‥} 縦棒で区切られた選択肢のどれでもよい
マルコフ圏の基本構造射*2の形状は次のように約束します。
| 射の種類 | 絵図での形状 |
|---|---|
| 恒等{射}? | ワイヤーだけ |
| {対称 | スワップ | 入れ替え | 交差}{射}? | 交差するワイヤー |
| {対角 | コピー | 分岐}{射}? | 分岐するワイヤー |
| {破棄 | デリート | 削除}{射}? | 途切れるワイヤー、終端にドット |
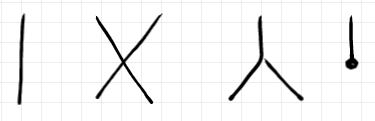
ノードの形状と塗りパターン
ノードの形状は、丸、四角、上トンガリ三角、下トンガリ三角を使います。三角形は特別なプロファイル(域と余域)を持つ射にしか使いません。
マルコフ圏においては、下トンガリ三角は破棄射しかないので、結局下トンガリ三角の出番はありません。プロファイル の射は菱形で描きますが、マルコフ圏では意味がないので菱形の出番もありません。
丸と四角は特にプロファイル制限がない射を表す目的で使います。が、丸や四角が特別なプロファイルになっても別にかまいません。
異なる射を区別するために、文字・文字列でラベルしてもいいですが、僕は“塗りパターン”で区別しています。
- 白抜き : ノード内部に何も描かない
- 塗り : 内部を塗る
- ベタ塗り : 黒く塗りつぶす
- 斜線塗り : 斜線で網掛け
- 格子塗り : 格子で網掛け
- 砂目塗り : 砂目で網掛け
さらに、ノードアイコンを半分に分けて片側だけ塗る“半塗り”も使います。単一形状に対して塗りパターンは21パターンあります。丸・四角と組み合わせて42種なので、ラテン文字によるラベリングの代用になります。

原則的に、白抜きと塗りは任意の射(射の自由変数)に対して使い、半塗りは何か特定的な射に対して使うことにしています。気持ちの上でのゆるい使い分けに過ぎませんが。
塗り/半塗りに拘る必要もなく、様々なアイコンの装飾を使って、射を区別したり特別な射を表したりできます。もちろん、文字・文字列ラベリングでもかまいません。三色ボールペンで描いているなら色も使えます。
圏論的オペレーター
圏論的オペレーター〈圏論的コンビネータ〉の表現は、ボックスを使う場合が多いです。例えば、モナドのクライスリ拡張オペレーターなら、射のノードを“拡張ボックス”で囲みます(以下の図)。ただし、対象と射を関手と自然変換に“格上げ”している図なので解釈は少しややこしいです(詳細は「絵算で見る、拡張スタイルのモナドとモノイド・スタイルのモナド」参照)。
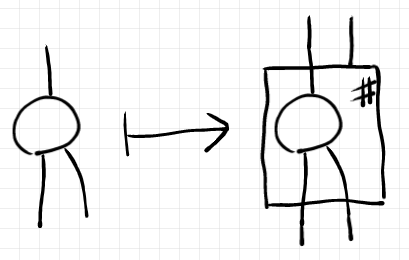
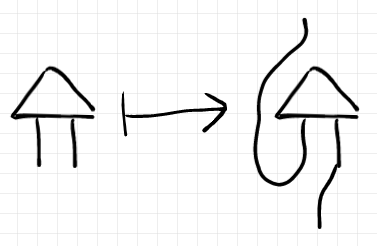
簡単なオペレーター〈コンビネータ〉の場合は、ワイヤーベンディング〈曲げ〉によってオペレーターの作用を表現できます。マルコフ圏の条件化オペレーターがその例で、描画方向「上から下/左から右」を仮定すれば、二本脚の上トンガリ三角の左脚を∪形に曲げる作用になります。
命題の記述
絵で描いた命題は、たいていはストリング図のあいだの等式です。が、たまに等しい〈同一性〉以外の関係を扱うことがあります。そのときは、絵図と相性がいい関係記号を前もって定義して使います。
マルコフ圏の2つの射に対して次の関係を定義しましょう。
上記の「 は
に関して
の反転である」という関係を、次の関係記号で表すことにします。
記号 を選んだのは、手書きで書きやすく絵との相性が良さそうだからで、特に深い理由はありません。
「 (網掛け四角)は
(網掛け三角)に関して
(丸)の反転である」の定義を絵で描くと次のようになります。
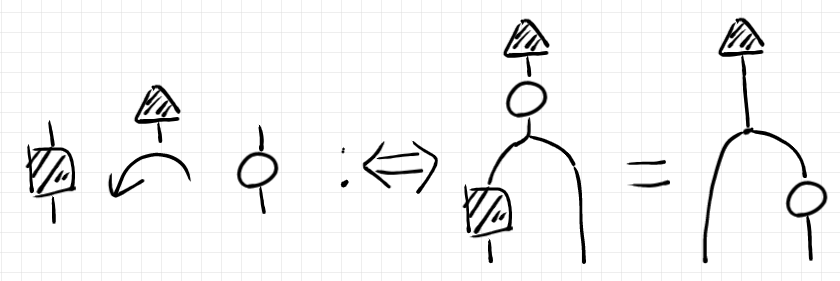
(丸)が与えられたとき、
である
(網掛け四角)が存在すれば、それは
(丸)のベイズ反転〈{Bayes | Bayesian} {converse | conversion | inverse | inversion}〉、または単に反転と呼びます。これはベイズ反転の公理的な特徴付け(あるいは公理的な規定)となります。
一方で、条件化可能なマルコフ圏の条件化オペレーターなどを使って構成的に定義された のベイズ反転は
と書くことにします。絵でも同様に、
のノードの右肩に
を(少し重ねて)乗せることにします。
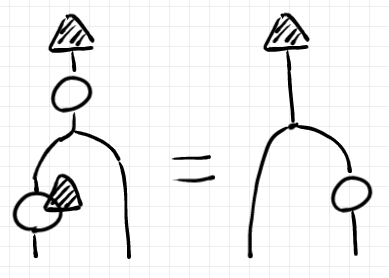
「構成的に定義されたベイズ反転 (丸の右肩に網掛け三角)が、公理的に規定されたベイズ反転になる」という内容の命題は次のように描けます。
定義の記述
は構成的に定義されたベイズ反転ですが、その実際の定義は以下のように描けます。
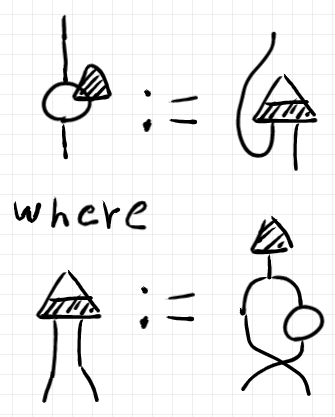
この定義内で出てきたワイヤーベンディング〈曲げ〉は条件化オペレーターの作用を表します。条件化オペレーターも公理的に規定できます。まず、「 は
の条件化である」を以下のように定義します。
また、適当に(ほんとにテキトーに)関係記号を選んでおきます。
無理に短い記号にしないで、自然言語風テキストそのままで "is a conditionalization of" と書いてもいいのですが、左右逆にした書き方 が書きにくいのがイヤなところ。
さて、 つまり「
(四角)は
(三角)の条件化である」の定義は、絵で次のように表せます。
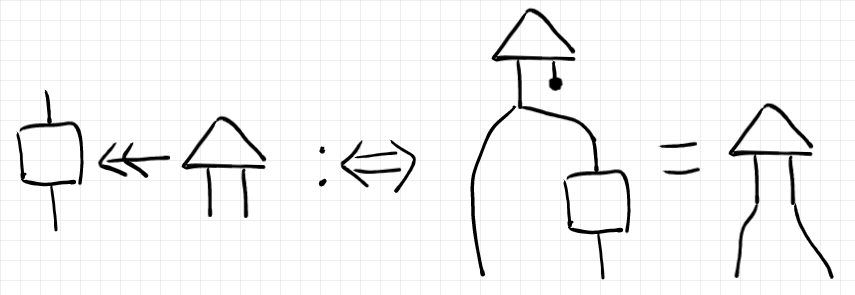
であるような
のことを
と書き、ワイヤーベンディングで描きます(そう約束する)。そのことを描けば次のようです。
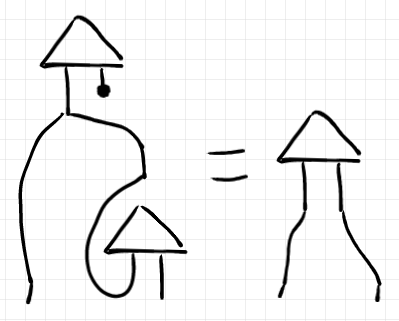
これは、与えられた (三角)に対する条件化
(左脚を曲げた三角)の公理的規定です。
関連した話題が以下の記事にあります。
計算と証明の記述
の絵による定義の一部に、次の中間的定義がありました。
この を
上半分下半分網掛け三角で描いていました*3。
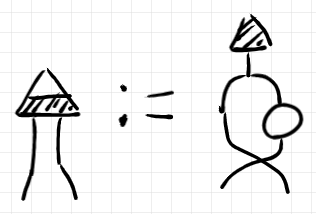
この を条件化すれば、条件化の公理的規定により次の等式が成立します。
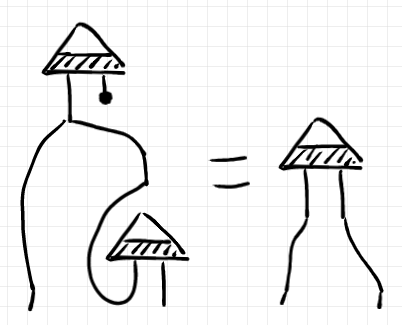
を定義により展開すれば次の等式になります。
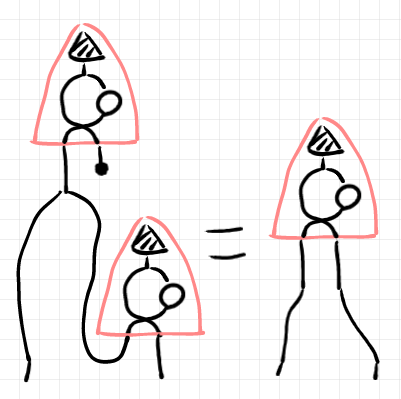
これは仮定や定義から成立しているのが分かっている等式です。
一方、「構成的に定義されたベイズ反転 が、公理的に規定されたベイズ反転になる」という内容の命題は次のように描けます。
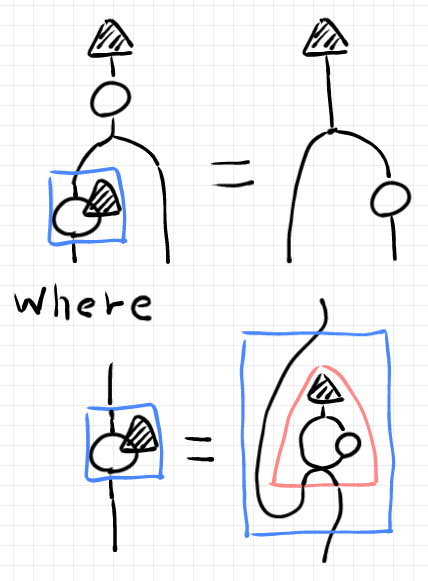
成立しているのが分かっている等式命題〈仮定 | 前提〉から、ターゲットの等式命題〈結論〉へとストリング図等式を“変形”すれば次の抽象的命題の証明が完了します。
- マルコフ圏が条件化可能〈conditionalizable〉なら反転可能〈convertible〉である。
興味があればチャレンジしてみてください。残っている作業は、ワイヤーの交差をハンドリングすること(置換計算)だけです。