レンズ/オプティックについて次の記事を書きました。
これらの記事を(読むのではなく)眺めてもらえれば分かると思いますが、レンズ/オプティックの記述・計算はストリング図なしではキビシイです。
レンズ/オプティックのストリング図を描くときの注意点を述べておきます。ストリング図の一般的なことは次の記事を参照してください。
内容:
描画方向と表記方向
モノイド圏におけるストリング図の描画方向は、射の結合の方向とモノイド積の方向で決まります。描画方向(の組み合わせ)は全部で8種類ありますが、射の結合の方向とモノイド積の方向の関係は2種類です。
射の結合の方向をx軸正方向に取ったとき、モノイド積の方向の取り方は次のどちらかです。
- 反時計回り規約: モノイド積の方向をy軸正方向に取る。モノイド積の左因子が下、右因子が上になる。
- 時計回り規約: モノイド積の方向をy軸負方向に取る。モノイド積の左因子が上、右因子が下になる。
反時計回り/時計回りのどちらかがわかっていれば、進行方向が揃った2本のワイヤーをテキストに書き下すことができます。例えば次の図:
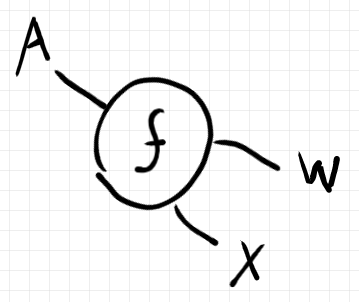
反時計回り規約であれば、 、時計回り規約であれば、
です。しかしワイヤーの方向が不明なので、次の可能性もあります。
レンズ/オプティックの描画では、描画方向を固定するのは無理ですが、反時計回りか時計回りかの規約を固定することはできます。僕は反時計回り規約で描くことが多いですが、常にそうしているわけでもないです。
の後に
を繋いだ〈結合した〉射は
または
と書きます。セミコロン(図式順演算記号)を使うかサークル(反図式順演算記号)を使うかは好みの問題で、意味的な違いはないです。
しかし、反対圏の結合演算は別物です。反対圏の結合を次の記号で表すとします。
を使うか
を使うかは好みの問題ですが、
と
、
と
は異なる圏の異なる結合演算です。
の対象・射をどのように区別して(あるいは区別しないで)描画・表記するか? 曖昧にしていると混乱することがあります。
モノイド積に関しても同様なことがあります。与えられたモノイド圏 に対して、
と定義されたモノイド積を持つ圏 を考えることができます。
と
は書き方の違いではなくて異なるモノイド圏の異なるモノイド積です。
たまに、モノイド積に関する“反変関手”が登場することがあります。例えば、次の同型が成立するような関手です。
順番を反対にしたモノイド積を使えば:
モノイド圏は特殊な2-圏とみなすことができますが、2つ以上の演算があると、反対圏の作り方が幾つもあり、その書き方に困ったりします。興味があれば次の記事を。
順行パートと逆行パートを左右に並べる描画法
「圏論的レンズ 2: 具象オプティック 」で次のように書きました
ロマン(Mario Roman)やライリー(Mitchell Riley)は、凹形の上下を逆にして描く方法を採用しています -- そういう描画法だと、結合〈composition〉の際にサイズの縮小・拡大をしなくてはならないので僕は嫌いです。
順行パートと逆行パートを左右に並べる描画法には、テキスト記法 と同じ配置になるというメリットもあるので、欠点を補正する方法を考えました。
ロマンやライリーの描画法と方向をあわせるには、次のどちらかの約束をします。
- 残余を左から掛ける。モノイド積の方向を時計回り規約で描く。
- 残余を右から掛ける。モノイド積の方向を反時計回り規約で描く。
どちらでも同じ絵になりますが、ロマンやライリーは「左から掛ける/時計回り規約」のようです。
テキスト記法と同じ配置になるとは次のことです。
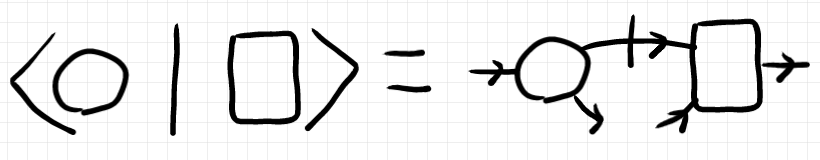
結合の際にサイズの縮小・拡大をしなくて済むように、ワイヤーを曲げておきます。
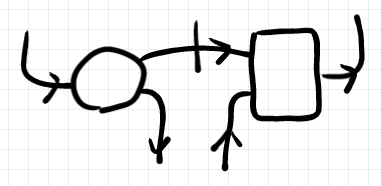
次のようにして結合します。
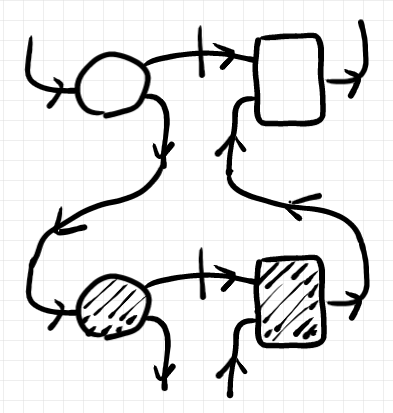
この描画法では、順行パートの方向は左から右でもあり、上から下でもあります。順行パートのモノイド積の順番は上から下で時計回り規約になっています。逆行パートは左から右/下から上で、モノイド積の順番は上から下で同じく時計回り規約になっています。
順行パートと逆行パートを上下に並べる描画法
過去の記事で僕が使っていた描画法は順行パートを上に置いて、反時計回り規約を採用したものです。
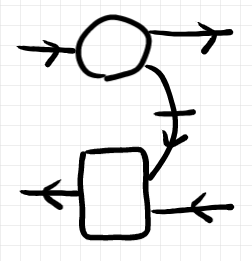
時計回り規約にしたい、つまり順行パートのモノイド積の順番を上から下にしたいなら、順行パートを下に配置すればいいでしょう。
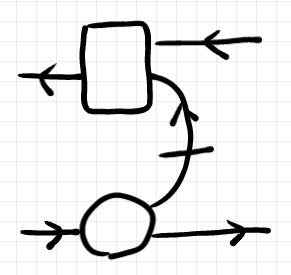
いずれの場合も順行方向を左から右に取っていますが、反図式順演算記号にあわせるために順行方向を右から左にとるのもアリっちゃアリです(僕は嫌だけど)。