「両側テレオロジー圏とプレオートマトン」にて:
両側テレオロジー圏は自己双対コンパクト閉圏とよく似た構造になります。テレオロジー圏とコンパクト閉圏には、親族的関連性があるのでしょう。
テレオロジー圏、コンパクト閉圏、トレース付きモノイド圏のあいだには親族的関連性があるようです。テレオロジー圏の(親族内での)位置付けはまだハッキリしませんが、コンパクト閉圏とトレース付きモノイド圏のあいだの関連性はよく知られています。
コンパクト閉圏は標準的にトレース付きモノイド圏です。トレース付きモノイド圏が与えられたとき、そのトレース付きモノイド圏からコンパクト閉圏を作る処方箋があります。それがInt構成(GoI構成ともいう)です。テレオロジー圏を含めた親族構造を探る準備として、Int構成を復習しておきます。
復習と言ったのは(そしてタイトルを「再論」としたのは)、Int構成はかなり昔から何度か話題にしているからです。$`\require{enclose}
\newcommand{\fwtimes}{ \enclose{circle}{\triangleright} }
\newcommand{\bwtimes}{ \enclose{circle}{\triangleleft} }
\newcommand{\cat}[1]{\mathcal{#1} }
\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\In}{\text{ in }}
`$
内容:
アブラムスキーの8の字結合
次の図はアブラムスキーの論文からのコピーです。
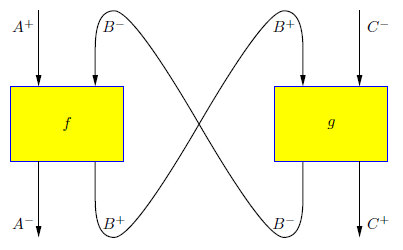
- Title: Abstract Scalars, Loops, and Free Traced and Strongly Compact Closed Categories
- Author: Samson Abramsky
- Submitted: 15 Oct 2009
- Pages: 32p
- URL: https://arxiv.org/abs/0910.2931
上記論文の p.24 に上の絵があります。過去のブログ記事でこの絵を引用しています。
- 2010-09-02: Webサービスの設計: Webフローの図示法を再考する
- 2010-09-21: Webサービスの設計:リンク集+お絵描きWeb設計
実は、この時期より前に同種の絵(アブラムスキーの別の論文からだろうが、今となっては不明)を手描きで引き写して使っています。
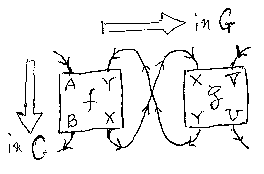
- 2006-07-21 キマイラサイト記事: Int(GoI)構成
- 2006-07-21 投稿報告: Int(GoI)構成
これらの絵が何を意味するかというと、縦方向に描いてあるトレース付きモノイド圏 $`\cat{C}`$ 内の射を横方向に結合して、別な圏 $`\cat{G}`$ の結合と考えようという事です。
Int構成〈GoI構成〉
$`\cat{C}`$ がトレース付きモノイド圏のとき、$`\cat{C}`$ をもとにしてコンパクト閉圏 $`\cat{G}`$ を構成する手続きがInt構成で、次のように書きます。
$`\quad \cat{G} = \mrm{Int}(\cat{C})`$
Intは整数〈integer〉のことで、自然数から整数を作る手順と似てるからです。そのことは、次の過去記事に書いています。
GoI構成はInt構成の別名で、Geometry of Interaction に由来します。
2003年の白旗さん、2004年の長谷川さんの論文に、Int構成が説明されています。
- Title: Geometry of Interaction explained (Algebra, Logic and Geometry in Informatics)
- Author: Shirahata, Masaru (白旗優)
- Date: 2003
- Pages: 28p
- URL: https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/43041/1/1318_19.pdf
- Title: The Uniformity Principle on Traced Monoidal Categories
- Author: Masahito Hasegawa (長谷川真人)
- Date: 2004
- Pages: 24p
- URL: https://www.kurims.kyoto-u.ac.jp/~hassei/papers/prims04.pdf
Int構成の射と結合の図示
Int構成では、$`\cat{C}`$ の射をもとにして、$`\cat{G}`$ の射を定義します。定義の仕方に「モノイド積をスイッチする方式」と「モノイド積をスイッチしない方式」があります。アブラムスキー論文と白旗論文はスイッチしない方式なので、こちらを先に説明します。
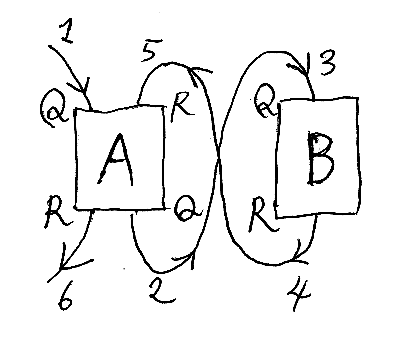
ストリング図で描けば、4本脚のノードを、縦方向の射とみなすか横方向の射とみなすかにより、$`\cat{C}`$ の射から $`\cat{G}`$ の射への変換を定義します。ただし、縦と横の選び方は恣意的です。次は白旗論文からの絵です。
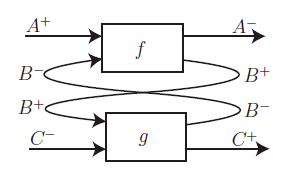
アブラムスキーの絵を時計回りに90度回転した反時計回りに90度回転してからモノイド積の方向も変更したレイアウトになっているので、「縦」と「横」の意味は変わってしまいます。いずれにしても、以下のような対応を考えます。
- $`A^+, A^-, B^+, B^- \in |\cat{C}|`$ とする。
- $`|\cat{G}| := |\cat{C} | \times |\cat{C}|`$
- $`\cat{C}`$ の射: $`f: A^+ \otimes B^- \to A^- \otimes B^+ \In \cat{C}`$
- $`\cat{G}`$ の射: $`f: (A^+, A^-) \to (B^+, B^-) \In \cat{G}`$
素朴に絵を眺めると、$`f: (A^+, A^-) \to (B^-, B^+)`$ のように見えるのですが、$`\cat{G}`$ での射の余域〈codomain〉はペアの順番を絵とは逆にします。この逆転を補正するために“8の字”が現れます。
長谷川論文 "Appendix B. The Int Construction" で紹介されている定義は、ほんの少し違います。
- $`\cat{C}`$ の射: $`f: A^+ \otimes B^- \to B^+ \otimes A^- \In \cat{C}`$ (ココの余域が違う)
- $`\cat{G}`$ の射: $`f: (A^+, A^-) \to (B^+, B^-) \In \cat{G}`$
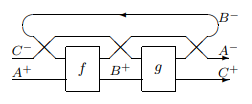
$`\cat{C}`$ の射としての $`f`$ の余域側のモノイド積の順序を入れ替え〈スイッチ〉しています。このことを明確化するために、次のような記号を導入しましょう。
$`\quad A \fwtimes B := A\otimes B\\
\quad A \bwtimes B := B\otimes A
`$
この記法を使うと「モノイド積をスイッチする方式」の対応は次のようです。
- $`\cat{C}`$ の射: $`f: A^+ \fwtimes B^- \to B^+ \bwtimes A^- \In \cat{C}`$
- $`\cat{G}`$ の射: $`f: (A^+, A^-) \to (B^+, B^-) \In \cat{G}`$
「モノイド積をスイッチする方式」による射と結合を絵に描いてみると次のようです。
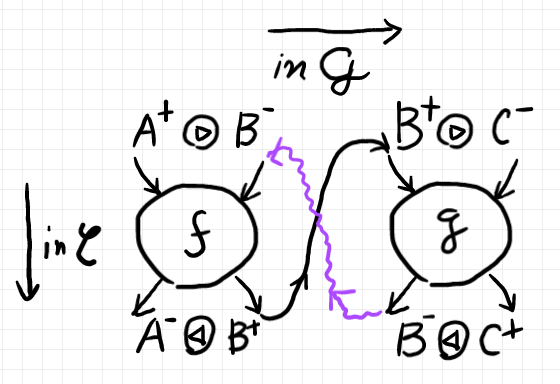
今までに出した絵とほぼ同じですが:
- $`\fwtimes`$ と $`\bwtimes`$ を使っている。
- 紫色の波線は、トレースにより繋ぐことを意味する。
「モノイド積をスイッチする方式」と「モノイド積をスイッチしない方式」の特徴は:
- モノイド積をスイッチする方式: 順番を変えたモノイド積 $`\bwtimes`$ を導入しないとスッキリした絵が描けない。が、$`\cat{G}`$ の恒等射が $`\cat{C}`$ の恒等射で書ける。
- モノイド積をスイッチしない方式: 特に工夫しなくてもスッキリした絵が描ける。が、$`\cat{G}`$ の恒等射は $`\cat{C}`$ の対称射〈symmetry〉で定義する必要がある。
このテの話だと、順番や向きの決め方はややこしくなります。抽象的・形式的には同じ定義でも、上下左右の約束や描画法のバリエーションは色々と生じます。以下は、「Webサービスの設計: Webフローの図示法を再考する」、「Webサービスの設計:リンク集+お絵描きWeb設計」に載せていた幾つかの絵です。
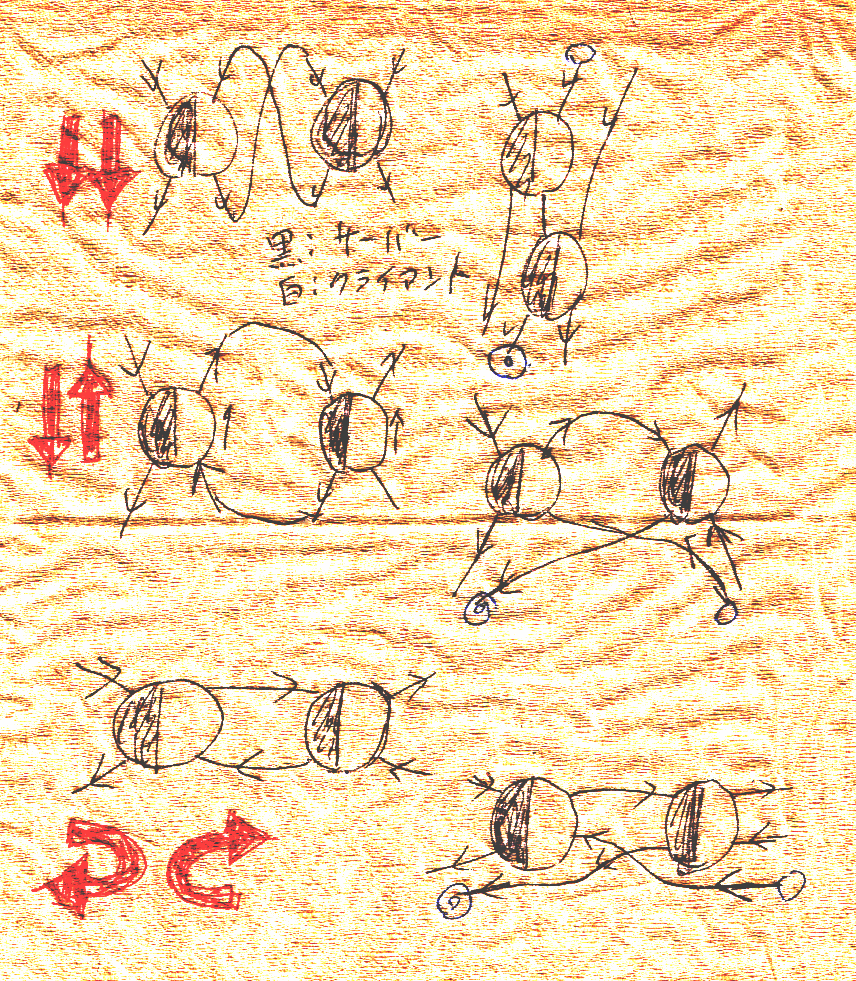
自由忘却随伴系?
コンパクト閉圏が持つ標準的なトレースとInt構成は、“コンパクト閉圏の圏”と“トレース付きモノイド圏の圏”のあいだの自由忘却随伴系〈free-forgetful adjunction〉のように思えます。多くの人がそれを前提にしているようなので、この自由忘却随伴系の存在はフォークロアのようです。
自由忘却随伴系の存在をちゃんと示すのはだいぶ面倒な感じはします。ちょっと探した結果では、次の論文(2022年)が自由構成をちゃんとやってるみたいです(読んでないので内容に言及できませんが)。
- Title: The free compact closure of a symmetric monoidal category
- Antonin Delpeuch
- Submitted: 19 Jan 2022 (v1), 21 Jan 2022 (v2)
- Pages: 12p
- URL: https://arxiv.org/abs/2201.07527 (なぜか現時点では論文がない)
- URL: https://www.researchgate.net/publication/357952845_The_free_compact_closure_of_a_symmetric_monoidal_category (ダウンロードページ: ファイルは The_free_compact_closure_of_a_symmetric_monoidal_c.pdf)