「層化ストリング図」では、"layer"を「層」としたのですが、「層」は"sheaf"の翻訳語であり、トラブルの原因になりそうなので「層」から「レイヤー」に変更します。ただし、過去の記事は変更しません*1。
で、レイヤー化ストリング図〈layered string diagram〉ですが、これは余インデックス付き圏/インデックス付き圏のトータル圏(「最近の型理論: 拡張包括構造を持ったインデックス付き圏」の最初の節参照)の対象・射・等式の描画に有効です。この記事で描画法をもう少し説明します。
一般的な余インデックス付き圏/インデックス付き圏を相手にするのは複雑なので、ベース圏〈インデキシング圏〉が順序集合の場合に限ります(ロブスキ/ザンサイ〈Leo Lobski, Fabio Zanasi〉論文もそのようなケースを扱っています)。また、局所圏〈ファイバー圏〉は対称厳密モノイド構造を持つとします。
レイヤー化ストリング図では、ほんとに新しい描画法はないのですが、キャンバスを分割〈スプリット〉する描画法が使い勝手が良いので、この描画法に注目することにします。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\twoto}{\Rightarrow}
\newcommand{\hyp}{\text{-}}
\newcommand{\In}{\text{ in }}
\newcommand{\rev}[1]{ {^\mathrm{rev}\!{#1}} }
\newcommand{\op}{\mathrm{op}}
`$
内容:
レイヤー化対称厳密モノイド圏
「層化ストリング図」で紹介/定義した用語は、だいたいそのまま使います(「層」は使いませんが)。ロブスキ/ザンサイ論文におけるレイヤー化プロップ〈layered prop〉は、どこまで構文論を含んでいるか判然としないので、意味論的構造はレイヤー化対称厳密モノイド圏〈layerd symmetric strict monoidal category〉と呼ぶことにします。
レイヤー化対称厳密モノイド圏は:
- 余インデックス付き圏 $`\cat{M}: \Omega \to {\bf SymStrMonCat}^1 \In {\bf CAT}`$ である。
- ベース圏〈インデキシング圏〉 $`\Omega`$ は、最小元を持つ順序集合(を圏とみなしたモノ)である。記号の乱用で $`\Omega = (\Omega, \le, \bot)`$ と書く。
$`\Omega`$ の射 $`f:\omega \to \tau`$ は域・余域だけで決まるので次の記法も使います。
$`\quad f = (\omega \le \tau) : \omega \to \tau \In \Omega`$
$`f`$ を $`\Omega^\op`$ の射とみなしたものを次のように書くとします。
$`\quad f^\op = (\tau \ge \omega) : \tau \to \omega \In \Omega^\op`$
余インデックス付き圏 $`\cat{M}`$ と一緒に、インデックス付き圏 $`\rev{M}`$ (「層化ストリング図」の最初の節参照)も考えます。
$`\quad \rev{\cat{M}}: \Omega^\op \to {\bf SymStrMonCat}^1 \In {\bf CAT}`$
次が成立します。
$`\quad \rev{\cat{M}}[f^\op] = \cat{M}[f] : \cat{M}[\omega] \to \cat{M}[\tau] \In {\bf SymStrMonCat}^1`$
次の用語を使うことにします。比喩的な表現に過ぎないので、国語辞書的意味や他分野の用法を強く連想しないように注意。
- $`\Omega`$ の対象をレイヤー〈layer〉と呼ぶ。
- $`\Omega`$ の射 $`f`$ と関手 $`\cat{M}[f]`$ を詳細化〈refinement〉と呼ぶ。
- $`\Omega^\op`$ の射 $`f^\op`$ と関手 $`\rev{\cat{M}}[f^\op]`$ を粗視化〈coarsening〉と呼ぶ。
レイヤー化対称厳密モノイド圏のトータル圏
レイヤー化対称厳密モノイド圏は余インデックス付き圏なので、グロタンディーク構成〈Grothendieck construction〉ができます。グロタンディーク構成によって出来上がる平坦化圏には順方向と逆方向があります。インデックス付き圏の場合と余インデックス付き圏の場合で合計4種類の平坦化圏があります(グロタンディーク構成と積分記号)。4種類の平坦化圏と対応する積分記号(平坦化のオペレータを表す)は:
- $`\int_\rightarrow`$ : インデックス付き圏の順方向平坦化圏
- $`\int_\leftarrow`$ : インデックス付き圏の逆方向平坦化圏
- $`\int^\rightarrow`$ : 余インデックス付き圏の順方向平坦化圏
- $`\int^\leftarrow`$ : 余インデックス付き圏の逆方向平坦化圏
レイヤー化対称厳密モノイド圏のトータル圏として使うのは次の圏です。
- $`\int^{\rightarrow\,\Omega} \cat{M}`$ : 余インデックス付き圏 $`\cat{M}`$ の順方向平坦化圏
- $`\int_{\leftarrow\,\Omega^\op} \rev{\cat{M}}`$ : インデックス付き圏 $`\rev{\cat{M}}`$ の逆方向平坦化圏
トータル圏の射は次のように書けます。
$`\text{For } f:\omega \to \tau \In \Omega\\
\quad F = (f, \varphi) : (\omega, A) \to (\tau, B) \In \int^{\rightarrow\,\Omega} \cat{M}\\
\quad \text{where }\varphi : \cat{M}[f](A) \to B \In \cat{M}[\tau]\\
\:\\
\text{For } f^\op: \tau \to \omega \In \Omega^\op\\
\quad F' = (f^\op, \psi) : (\omega, A) \to (\tau, B) \In \int_{\leftarrow\,\Omega^\op} \rev{\cat{M}}\\
\quad \text{where }\psi : \rev{\cat{M}}[f^\op](A) \to B \In \cat{M}[\tau]
`$
次の略記も使います。
- $`f_* \hyp := \cat{M}[f](\hyp)`$ ($`f`$ による前送り)
- $`(f^\op)^* \hyp := \rev{\cat{M}}[f^\op](\hyp)`$ ($`f^\op`$ による引き戻し)
$`f_*`$ と $`(f^\op)^*`$ はまったく同じ関手です。
関手スプリッターとスプリット図
「層化ストリング図」で述べたように、レイヤー化ストリング図では、関手ボックス/関手コボックスとその変種を用います。関手ボックス(または関手コボックス)のサイズを大きくすると、関手ボックスの境界がキャンバスを二分するように見えます(下図)。
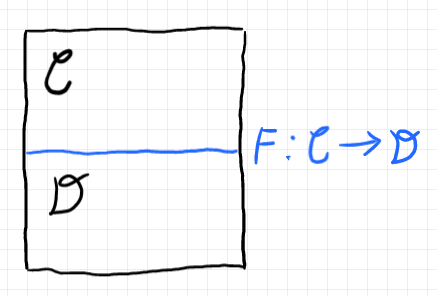
このとき、キャンバスを二分している境界線を関手スプリッター〈functor splitter〉と呼ぶことにします。そして、関手スプリッターを使った図をスプリット図〈split diagram〉と呼びましょう。繰り返しますが、関手スプリッターは関手ボックスのサイズ/レイアウトを変えただけのものです。関手ボックス/関手コボックスと同じ情報を表現します。
余インデックス付き圏 $`\cat{M}`$ のグロタンディーク平坦化圏 $`\int^{\rightarrow\,\Omega} \cat{M}`$ の射(トータル射) $`(f, \varphi) : (\omega, A) \to (\tau, B)`$ は次のように描きます。
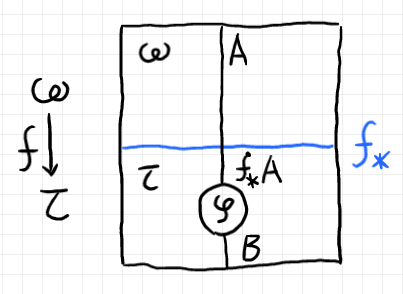
- 圏を表すキャンバスの領域は、レイヤー(ベース圏の対象)でラベルする。
- 詳細化関手は関手スプリッターとして描く。
- ワイヤー(圏の対象)が関手スプリッターを通り抜けるとき、詳細化関手が適用されるとする。
一般化
すぐに思いつく一般化の候補があります。
- ベース圏を順序集合に限らず一般的な圏にする。
- 局所圏を、厳密とは限らない対称モノイド圏とする。
- 局所圏を、対称とは限らないモノイド圏とする。
- 余インデックス付き圏ではなくてインデックス付き圏からはじめて順方向平坦化圏を使う。
すぐ思いつく割には、どれも自明ではなくて、けっこう面倒そうです。
これらの一般化より前に、レイヤー化対称厳密モノイド圏をモデルとするようなシーケント計算を整備したほうがいいかも知れません。
*1:ブログ記事は記録として残したいので、できるだけ“書いた当時のまま”にしておきたいのです。