今年〈2023年〉の夏くらいから、絵図的手法のフレームワークとして、スケマティック系というものを考え始めました。スケマティック系に関連する記事は「スケマティック系のハブ記事」からたどれます。
スケマティック系の素材として、半グラフやバエズ/ドーラン・ツリーなどを調べてみたのですが、これらの構造の背後に、比較的単純な代数系があるようです。絵図(ストリング図/ワイヤリング図)の切り貼りを支配している代数系です。この代数系(“貼り合わせ代数”と呼びます)について述べます。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\u}[1]{\underline{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\bdry}{\partial }
\newcommand{\bdryD}{\widetilde{\partial\,} } % D = diagram
\newcommand{\hatotimes}{\widehat{\otimes}}
%\newcommand{\Imp}{\Rightarrow }
%\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{-} }
\newcommand{\dimU}[2]{{#1}\!\updownarrow^{#2}}
\newcommand{\BoxSum}{ \mathop{\Box} }
\newcommand{\BoxCSum}[3]{ \mathop{_{#1} \overset{#2}{\Box} _{#3}} } % cofibred sum
\newcommand{\ASum}[3]{ \mathop{_{#1} \overset{#2}{+} _{#3}} } % amalgamated sum
`$
内容:
はじめに
ダンクソ/ハラーチェバ/ロバーツォン〈Zsuzsanna Dancso, Iva Halacheva, Marcy Robertson〉のワイヤリング図のオペラッド(「回路代数とグラフ置換モナド」参照)、コステロ〈Kevin Costello〉の半グラフの圏(「亜群をベースとする圏類似構造: コステロの事例」参照)、ボリソフ/マニン〈D. Borisov, Yu. I. Manin〉の半グラフの圏(「半グラフの二重圏と半グラフ変形」参照)など、それぞれにうまく出来てるなと思いますが、なにか共通の代数構造があって、それを別な側面から見ているような印象を受けます。
共通の代数構造とは、ストリング図/ワイヤリング図を被演算対象物〈オペランド〉とするような計算体系です。演算〈オペレーター/オペレーション〉はストリング図/ワイヤリング図に対して働くわけですが、描かれた図画〈drawing | figure | picture〉そのものに働くというよりは、キャンバスに働くと考えたほうがよさそうです。キャンバスを貼り合わせることにより、結果的に図画も繋がって合成される、ということです*1。
つまり、「被演算対象物〈オペランド〉はストリング図/ワイヤリング図が描かれたキャンバスであり、演算はキャンバスの貼り合わせ」であるような代数構造に注目するのがよいと思います。このような代数構造を貼り合わせ代数と呼ぶことにします。
貼り合わせ代数は、絵図的手法のフレームワークとしたいので、直感が働くように幾何的ベースを持つべきです。が、ある程度は公理化しないと取り扱いが難しいでしょう。幾何的ベースとして、2次元以下のコンパクト多様体の圏 $`{\bf KMan}^{\le 2}`$ (後述)を採用し、公理化の方針としてはモナドのアイレンベルク・ムーア代数としての定式化を目指します。
図式の圏
Diag構成を使います。Diag構成については以下の記事で書いています。
- Diag構成: 圏論的構成法の包括的フレームワークとして
- Diag構成の変種とその書き方 -- 反変図式と逆向きの図式について書いていますが、この記事では反変/逆向きは使いません。
「図式〈diagram〉」は多義語ですが、主に、Diag構成で作られた圏〈図式の圏〉の対象の意味で使います。まず、ここで使う“図式の圏”の“形状の圏”を定義しましょう。
$`{\bf FinGraph}`$ は、有限有向グラフの圏だとします。グラフが「有限」とは、頂点集合も辺集合も有限集合であることです。この記事内での「グラフ」は、有限有向グラフのことです。圏と同じ記法を使って、グラフ $`G`$ の頂点集合を $`|G|`$ 、二頂点 $`a, b`$ のあいだの辺〈有向辺〉の集合を $`G(a, b)`$ と書きます。グラフのあいだの準同型写像 $`f`$ は次のように書きます。
$`\quad f:G \to H \In {\bf FinGraph}\\
\quad f_\mrm{vert} : |G| \to |H| \In {\bf FinSet}\\
\text{For }a, b \in |G|\\
\quad f_\mrm{a, b} : G(a, b) \to H(f_\mrm{vert}(a), f_\mrm{vert}(b)) \In {\bf FinSet}
`$
任意のニ頂点 $`a, b\in |G|`$ に対して、$`f_{a, b}`$ が単射になるとき、グラフ準同型写像 $`f`$ は忠実〈faithful〉だといいます(これも圏論と同じ)。忠実準同型写像がさらに、$`f_\mrm{vert}`$ が単射なら埋め込み〈embedding〉と呼びます。
グラフ〈有限有向グラフ〉を対象として、埋め込みを射とする圏を $`{\bf FinGraphEmb}`$ とします。名前が長いので $`{\bf FGE}`$ という略称も使います。$`{\bf FinGraph}`$ も $`{\bf FG}`$ と略記します。
グラフから自由圏〈パスの圏〉を作る関手を、$`{\bf FG}, {\bf FGE}`$ 上で考えたものを、名前 $`\mrm{FreeCat}`$ をオーバーロードして書きます。
$`\quad \mrm{FreeCat}: {\bf FG} \to \dimU{\bf CAT}{1}\In \mathbb{CAT}\\
\quad \mrm{FreeCat}: {\bf FGE} \to \dimU{\bf CAT}{1}\In \mathbb{CAT}
`$
ここで、$`\dimU{\bf CAT}{1}`$ は、2-圏の2-射を捨てた1-圏です。$`\dimU{\text{-}}{1}`$ については「圏の次元調整」を参照してください。
以上の定義で、形状の圏 $`({\bf FG}, \mrm{FreeCat}), ({\bf FGE}, \mrm{FreeCat})`$ が定義できたので、Diag構成の準備ができました。次のDiag構成を考えます。
$`\quad {\bf CAT}\text{-}\mrm{Diag}^{ {\bf FG}, \mrm{FreeCat} }(\hyp): \dimU{\bf CAT}{1} \to \dimU{\bf CAT}{1} \In \mathbb{CAT}`$
以下では、このDiag構成を単に $`\mrm{Diag}^{\bf FG}(\hyp)`$ と書きます。$`\mrm{Diag}^{\bf FGE}(\hyp)`$ も同様です。右肩にグラフの圏を乗せて書きます。
グラフの圏の部分圏として、$`{\bf FDG}, {\bf FDGE}`$ もよく使います。名前内の D は有限離散グラフ〈finite discrete graphs〉を表し、E は埋め込み〈embeddings〉を表します。離散グラフは辺を持たないグラフなので、圏 $`{\bf FDG}`$ は有限集合の圏、圏 $`{\bf FDGE}`$ は有限集合と単射〈injection〉の圏と同型な圏になります。
$`\quad {\bf FDG} \cong {\bf FinSet} \In {\bf CAT}\\
\quad {\bf FDGE} \cong {\bf FinSetInj} \In {\bf CAT}
`$
$`{\bf FDG}`$ と $`{\bf FinSet}`$ 、$`{\bf FDGE}`$ と $`{\bf FinSetInj}`$ は同一視して(イコールだと思って)かまいません。実際、同一視した記述をするでしょう。
図式の演算
この節では、$`S, T \in |\mrm{Diag}^{\bf FG}(\cat{C})|`$ に対して、次のような演算を定義します。
- $`S \BoxSum T`$
- $`S \BoxCSum{i}{A}{j} T`$
まず、$`S`$ が図式とは、次のいずれかのことです(どっちでも同値)。
- $`S : \mrm{FreeCat}(G) \to \cat{C} \In {\bf CAT}`$
- $`S : G \to U(\cat{C}) \In {\bf GRAPH}`$ ($`U`$ は忘却関手)
しかし、横着して(記号の乱用で)次のようにも書きます。不正確な表現なので要注意。
- $`S : G \to \cat{C} \In {\bf CAT}`$
さて、図式のあいだの演算 $`\BoxSum`$ を定義しましょう。グラフの圏 $`{\bf FG}`$ は、グラフ(対象)の直和と準同型写像(射)の直和でモノイド圏になります。モノイド単位は空グラフです。このモノイド構造を備えた“グラフのモノイド圏”を $`({\bf FG}, +, 0)`$ とします。
$`S, T`$ が次のような図式だとします。
$`\quad S : G \to \cat{C} \In {\bf CAT}\\
\quad T : H \to \cat{C} \In {\bf CAT}
`$
このとき、直和グラフ $`G + H`$ 上の図式が誘導されます。図式 $`S, T`$ の余デカルト・コペアリング(デカルト・ペアリングの双対)です。コペア図式を次のように書きます。
$`\quad S \BoxSum T : G + H \to \cat{C} \In {\bf CAT}`$
$`\iota^{G, H}_1, \iota^{G, H}_2`$ をグラフの直和に伴う入射〈余射影〉だとすると、次の等式が成立します。
$`\quad \iota^{G, H}_1 * (S \BoxSum T) = S \;: G \to \cat{C} \In {\bf CAT}\\
\quad \iota^{G, H}_2 * (S \BoxSum T) = T \;: H \to \cat{C} \In {\bf CAT}
`$
ここで、'$`*`$' は、グラフの準同型写像(この場合は埋め込み)と図式の結合記号(図式順)です。
二項演算 $`\BoxSum`$ を図式のあいだの射にまで拡張して、図式の圏 $`\mrm{Diag}^{\bf FG}(\cat{C})`$ に対称モノイド構造を定義できます。単位対象は、空グラフからの唯一の図式 $`\u{0}`$ です。この対称モノイド圏は $`(\mrm{Diag}^{\bf FG}(\cat{C}), \BoxSum, \u{0})`$ と書きます。
次に、$`\BoxSum`$ より少し複雑な、しかし類似の演算を定義します。$`A, i, j`$ は、次のようなグラフと埋め込みだとします。
$`\quad A \in |{\bf FinSet}| = |{\bf FDG}| \subseteq |{\bf FG}|\\
\quad i: A \to G \In {\bf FGE} \subseteq {\bf FG}\\
\quad j: A \to H \In {\bf FGE} \subseteq {\bf FG}
`$
$`A`$ は離散グラフです。$`i, j`$ は埋め込みです。離散グラフ/埋め込みでなくても定義はできますが、今回は離散グラフ/埋め込みのケースしか使いません。$`S, T`$ は以下のような図式だとします。
$`\quad S : G \to \cat{C} \In {\bf CAT}\\
\quad T : H \to \cat{C} \In {\bf CAT}\\
\quad i * S = j * T \;: A \to \cat{C} \In {\bf CAT}`$
上の3行目は、$`S, T`$ に関する整合性条件で、この条件がないと演算 $`\BoxCSum{i}{A}{j}`$ を実行できません。$`S \BoxCSum{i}{A}{j} T`$ は、グラフの融合和〈amalgamated sum〉(ファイバー積の双対、プッシュアウト) $`G \ASum{i}{A}{j} H`$ の上で定義されます。
$`\quad S \BoxCSum{i}{A}{j} T : G \ASum{i}{A}{j} H \to \cat{C} \In \cat{C}`$
$`\BoxSum`$ と同様に、次の等式が成立します。
$`\quad \iota^{G\leftarrow A\to H}_1 * (S \BoxCSum{i}{A}{j} T) = S \;: G \to \cat{C} \In {\bf CAT}\\
\quad \iota^{G\leftarrow A\to H}_2 * (S \BoxCSum{i}{A}{j} T) = T \;: H \to \cat{C} \In {\bf CAT}
`$
先に定義した $`\BoxSum`$ は、今定義した演算の特別な場合です。$`\u{0}: 0 \to G`$ は、空グラフからの唯一の埋め込みとします。
$`\quad S \BoxSum T = S \BoxCSum{\u{0}}{0}{\u{0}} T \;: G + H \to \cat{C} \In {\bf CAT}
`$
2次元までのコンパクト多様体の圏
貼り合わせ代数の具体例を作るために、2次元までのコンパクト多様体の圏を導入します。2次元までのコンパクト多様体の圏については「バエズ/ドーラン茂みの対称モノイド亜群 // 2次元までの多様体の圏」で説明しています。過去記事では、コンパクト多様体の圏を単に $`{\bf Man}`$ としましたが、「コンパクト」であることを明示して $`{\bf KMan}`$ とします。K が「コンパクト」の略です。C にしなかったのは、C を「連結」の略に使うかも知れないからです。
2次元までのコンパクト多様体の圏を $`{\bf KMan}^{\le 2}`$ と書きます。$`{\bf KMan}^{\le 2}`$ の対象は次の性質を持ちます。
- コンパクトである。
- 連結とは限らない。
- 境界を持つかも知れない。
- 可微分構造を持つ。
- 向き付け可能でなくてもよい。
- 次元は2次元以下である。
コンパクト性を仮定しているので、開区間や全平面($`{\bf R}^2`$)は $`{\bf KMan}^{\le 2}`$ に入ってません。向き付け可能性〈orientable〉を仮定してないので、メビウス・バンドやクラインボトルも入っています。
$`{\bf KMan}^{\le 2}`$ の射は、境界を境界に移し〈写し〉ます。$`{\bf KMan}^{\le 2}`$ 内では、以下の図式は意味を持ち、可換です。ラベルがない縦方向の射は境界の包含写像です。
$`\require{AMScd}
\quad \begin{CD}
M @>{f}>> N \\
@AAA @AAA \\
\bdry M @>{f|_{\bdry M}}>> \bdry N
\end{CD}
`$
射が境界を保存するので、境界作用素 $`\bdry`$ は、次のような関手になります。
$`\quad \bdry : {\bf KMan}^{\le 2} \to {\bf KMan}^{\le 2} \In {\bf CAT}`$
境界となる多様体は境界がない(境界が空多様体である)ので、次が成立します。
$`\quad \bdry * \bdry = 0 \;\text{ where } 0 : {\bf KMan}^{\le 2} \to {\bf KMan}^{\le 2} \In {\bf CAT}\\
\quad \bdry \, 0 = 0 \;\text{ where } 0 \in |{\bf KMan}^{\le 2}|
`$
多様体の直和により $`{\bf KMan}^{\le 2}`$ は対称モノイド圏になります。記号の乱用で次のように書きます。
$`\quad {\bf KMan}^{\le 2} = ({\bf KMan}^{\le 2}, +, 0)`$
境界作用素は、対称モノイド積に関してモノイド関手になります。
$`\text{For }M, N \in |{\bf KMan}^{\le 2}|\\
\quad \bdry (M + N) \cong \bdry M + \bdry N \In {\bf KMan}^{\le 2}
`$
境界となり得る多様体*2の連結成分である多様体をボーダー多様体〈border manifold〉、または単にボーダー〈border〉と呼ぶことにします。多様体 $`N`$ がボーダーであるとは、以下のいずれかのことです。
- $`N \cong \mrm{pt} \;\In {\bf KMan}^{\le 2}`$ ($`\mrm{pt}`$ は一点だけからななる多様体)
- $`N \cong S^1 \;\In {\bf KMan}^{\le 2}`$
定義から、$`\bdry M`$ は幾つか(0個でも1個でもよい)のボーダーの直和になります。
多様体 $`M \in |{\bf KMan}^{\le 2}|`$ の連結成分の集合を $`\mrm{CC}(M)`$ と書くことにします(CC は connected components から)。これは、0次のホモトピー集合と同じです。
$`\quad \mrm{CC}: {\bf KMan}^{\le 2} \to {\bf FinSet} \In {\bf CAT}\\
\text{For }M \in |{\bf KMan}^{\le 2}| \\
\quad \mrm{CC}(M) := \pi_0(M) \;\in |{\bf FinSet}|
`$
多様体 $`M`$ の連結成分への直和分解は次の形に書けます。
$`\quad M = \sum_{L\in \mrm{CC}(M)} L`$
$`\mrm{CC}(M) = \emptyset`$ のとき、$`M = 0`$ (空多様体)です。
境界図式関手
境界作用素関手 $`\bdry : {\bf KMan}^{\le 2} \to {\bf KMan}^{\le 2}`$ の情報を精密化した関手 $`\bdryD`$ を定義します。
$`\quad \bdryD : {\bf KMan}^{\le 2} \to \mrm{Diag}^{\bf FG}({\bf KMan}^{\le 2}) \In {\bf CAT}`$
多様体 $`M`$ に対して $`\bdryD M`$ は多様体ではなくて、図式になります。図式には、その形状となるグラフが必要なので、$`\bdryD M`$ の形状グラフを定義しましょう。記法の単純化のために、次のように置きます。
$`\quad G := \mrm{dom}(\bdryD M) \;\in |{\bf FG}|`$
グラフ $`G`$ の頂点集合は次のようになります。
$`\quad |G| := \mrm{CC}(M) + \mrm{CC}(\bdry M) \; \in |{\bf FinSet}|`$
$`M`$ の連結成分の集合と、$`\bdry M`$ の連結成分の集合の直和が頂点集合になります。辺は次のルールで決めます。
- $`B \in \mrm{CC}(\bdry M)`$ と $`L \in \mrm{CC}(M)`$ に対して、$`B \subseteq \bdry L`$ のとき、$`B`$ から $`L`$ に向かう辺があるとする。
- それ以外の辺はない。
この定義から、$`G = \mrm{dom}(\bdryD M)`$ はやせたグラフ(ニ頂点のあいだの辺が高々一本のグラフ)です。マルチコスパン(余脚が2本とは限らないコスパン)の言葉を使うと、グラフ $`G`$ は次のように記述できます。
- $`M`$ の連結成分 $`L \in \mrm{CC}(M)`$ ごとにひとつのマルチコスパンがある。
- マルチコスパンの余ボディ〈cobody〉(スパンのボディの双対)は、$`L \in \mrm{CC}(M)`$ である。
- $`L`$ を余ボディとするマルチコスパンの余足〈cofoot〉(スパンの足の双対)は、$`B \subseteq \bdry L`$ となる $`B \in \mrm{CC}(L)`$ である。
- $`\bdry L`$ の連結成分の個数が、$`L`$ を余ボディとするマルチコスパンの余脚〈coleg〉の本数になる。
図式 $`\bdryD M: G \to {\bf KMan}^{\le 2}\In {\bf CAT}`$ の割り当てルールは次のようになります。
- 頂点 $`L \in \mrm{CC}(M) \subseteq |G|`$ には、$`L`$ 自体を対応させる。
- 頂点 $`B \in \mrm{CC}(\bdry M) \subseteq |G|`$ には、$`B`$ 自体を対応させる。
- $`B`$ から $`L`$ に至る辺には、包含 $`B \subseteq L`$ の包含写像を対応させる。
多様体のあいだの写像 $`f:M \to N \In {\bf KMan}^{\le 2}`$ があると、$`f`$ は連結成分を連結成分に移し、境界は境界に移すことから、形状グラフのあいだの準同型写像と図式のあいだの射が誘導されます。
$`\quad \bdryD f : \bdryD M \to \bdryD N \In \mrm{Diag}^{\bf FG}({\bf KMan}^{\le 2})`$
このことから、$`\bdryD`$ は関手であることが分かります。
$`{\bf KMan}^{\le 2}`$ と $`\mrm{Diag}^{\bf FG}({\bf KMan}^{\le 2})`$ はそれぞれ対称モノイド圏でした。$`\bdryD`$ は、対称モノイド関手にもなっています。
$`\quad \bdryD : ({\bf KMan}^{\le 2}, +, 0) \to (\mrm{Diag}^{\bf FG}({\bf KMan}^{\le 2}), \BoxSum, \u{0}) \In {\bf SymMonCAT}`$
マッチング図式
$`N \in |{\bf KMan}^{\le 2}|`$ がボーダーであるとは、$`N`$ が“一点”であるか“円周と同型”かのどちらかのことでした。ボーダーだけを対象とする $`{\bf KMan}^{\le 2}`$ の充満部分圏を $`{\bf KMan}^{\le 2}_\mrm{border}`$ とします。また、連結な多様体(空多様体は含めない)だけを対象とする $`{\bf KMan}^{\le 2}`$ の充満部分圏を $`{\bf KMan}^{\le 2}_\mrm{conn}`$ とします。定義より:
$`\quad {\bf KMan}^{\le 2}_\mrm{border} \subseteq {\bf KMan}^{\le 2}_\mrm{conn} \In {\bf CAT}`$
多様体 $`M \in |{\bf KMan}^{\le 2}|`$ に対して、$`M`$ 上のマッチング図式〈matching diagram〉という図式を定義します。マッチング図式は、$`M`$ に対して一意的に決まる図式ではなくて、マッチング図式の集合が決まります。つまり、$`M`$ に対して、$`|\mrm{Diag}^{\bf FG}({\bf KMan}^{\le 2})|`$ の部分集合が決まります。
マッチング図式は $`m`$ などで表します -- 大文字だと多様体と誤認のリスクがあるので。
$`\quad m: \mrm{dom}(m) \to {\bf KMan}^{\le 2} \In {\bf CAT}`$
$`\mrm{dom}(m)`$ は、本来はグラフから作った自由圏ですが、記号の乱用でグラフそのものを表すとします。$`G := \mrm{dom}(m)`$ と置くと、$`G`$ は次のようなグラフです。
- $`|G| = \mrm{CC}(M) + V`$ 、ここで、$`V`$ は有限集合。
- $`G`$ はやせたグラフ〈単純グラフ〉である。つまり、2頂点のあいだの辺は高々1本。
- 辺は、$`V`$ の要素から $`\mrm{CC}(M)`$ の要素に向かうものだけ。
- 任意の $`v \in V`$ から出る辺が少なくとも1本はある。
- 任意の $`L \in \mrm{CC}(M)`$ に入る辺は高々1本。
$`G`$ は、頂点集合が2つの部分に分かれているので二部単純グラフです。出る辺の数である $`\mrm{outdeg}(\hyp)`$ (out degree)と入る辺の数である $`\mrm{indeg}(\hyp)`$ (in degree)を使うと、上記の条件は次のように書けます。
$`\quad \forall v\in V.\, \mrm{outdeg}(v) \ge 1 \land \mrm{indeg}(v) = 0\\
\quad \forall L\in \mrm{CC}(M).\, \mrm{outdeg}(L) = 0 \land \mrm{indeg}(L) \le 1
`$
$`v\in V`$ に対して、$`v`$ から出る辺の集まりは、マルチスパン(脚が2本とは限らないスパン)になります。このマルチスパンを、マッチング図式のマッチャー〈matcher〉と呼びます。これは、「半グラフに関わる諸概念 // マッチャー」で述べたマッチャーと同じ役割を持つ概念です。
マッチング図式の形状グラフ $`G`$ のマッチャーが、(マルチスパンとしての)脚が2本のとき非特異マッチャー〈nonsingular matcher〉と呼びます。脚が2本ではないマッチャーは特異マッチャー〈singular matcher〉です。すべてのマッチャーが非特異である形状グラフ、あるいはそのような形状グラフを持つマッチング図式は非特異〈nonsingular〉といいます。ひとつでも特異マッチャーを持つ形状グラフ/マッチング図式は特異〈singular〉です。
$`M`$ 上のマッチング図式 $`m: G \to {\bf KMan}^{\le 2} \In {\bf CAT}`$ の割り当てルールは次です。
- $`L \in \mrm{CC}(M)`$ には、$`L`$ 自体を対応させる。
- $`v \in V`$ には、$`{\bf KMan}^{\le 2}_\mrm{border}`$ の対象を対応させる。
- 辺には、$`{\bf KMan}^{\le 2}_\mrm{border}`$ の同型射を対応させる。
グラフ $`G`$ の辺 $`e`$ に対して $`m(e) \in \mrm{Mor}({\bf KMan}^{\le 2})`$ は、両端がボーダーである同型射です。したがって、マッチング図式は、ベースとなる多様体 $`M`$ とグラフ $`G`$ で事実上決定されてしまいます。
多様体 $`M \in |{\bf KMan}^{\le 2}|`$ 上のすべてのマッチング図式の集合を $`\mrm{MatchD}[M]`$ とします。
$`\text{For }M \in |{\bf KMan}^{\le 2}|\\
\quad \mrm{MatchD}[M] \subseteq |\mrm{Diag}^{\bf FG}({\bf KMan}^{\le 2})| \In {\bf SET}
`$
丸括弧の $`\mrm{MatchD}(\hyp)`$ は別な意味で使う予定なので、角括弧〈ブラケット〉を使っています。
貼り合わせ図式
多様体 $`M \in |{\bf KMan}^{\le 2}|`$ に対して、その境界図式 $`\bdryD M`$ は一意的に決まります。$`M`$ 上のマッチング図式の集合 $`\mrm{MatchD}[M]`$ も集合として一意的に決まります。これらの図式を使うと、貼り合わせ図式は簡単に定義できます。
マッチング図式 $`m \in \mrm{MatchD}[M]`$ の形状グラフ $`\mrm{dom}(m)`$ は、$`\mrm{CC}(M)`$ を離散部分グラフとして含みます。また、境界図式 $`\bdryD M`$ の形状グラフも、$`\mrm{CC}(M)`$ を離散部分グラフとして含みます。グラフの包含写像を $`i, j`$ とすると、次のようになります。
$`\quad i : \mrm{CC}(M) \to \mrm{dom}(\bdryD M) \In {\bf FGE}\\
\quad j : \mrm{CC}(M) \to \mrm{dom}(m) \In {\bf FGE}
`$
したがって、図式の演算として $`{\bdryD M}\BoxCSum{i}{\mrm{CC}(M)}{j} m`$ を構成可能です。包含写像 $`i, j`$ が了解されているなら $`{\bdryD M}\BoxCSum{}{\mrm{CC}(M)}{} m`$ と書いてもかまいません。こうして構成された図式を($`M`$ 上の)貼り合わせ図式〈gluing diagram〉と呼びます。$`M`$ 上のすべての貼り合わせ図式の集合を $`\mrm{GluD}[M]`$ とします。
定義から分かるように、$`M`$ 上のマッチング図式に境界図式をアタッチすると貼り合わせ図式ができるので、マッチング図式と貼り合わせ図式は一対一対応します。
$`\quad \mrm{GluD}[M] \cong \mrm{MatchD}[M] \In {\bf SET}`$
$`\mrm{GluD}[M]`$ は、$`|\mrm{Diag}^{\bf FG}({\bf KMan}^{\le 2})|`$ の部分集合なので、図式の同型により商集合を作ることができます。商集合には下線を引くことにします*3。
$`\quad \u{\mrm{GluD}}[M] := \mrm{GluD}[M]/\!\cong `$
図式の同型類の集合 $`\u{\mrm{GluD}}[M]`$ は小さい集合になります。
$`\quad \u{\mrm{GluD}}[M] \in |{\bf Set}|`$
実例の絵
前節で説明した貼り合わせ図式と、次節で説明する貼り合わせ演算の実例を絵で示します。
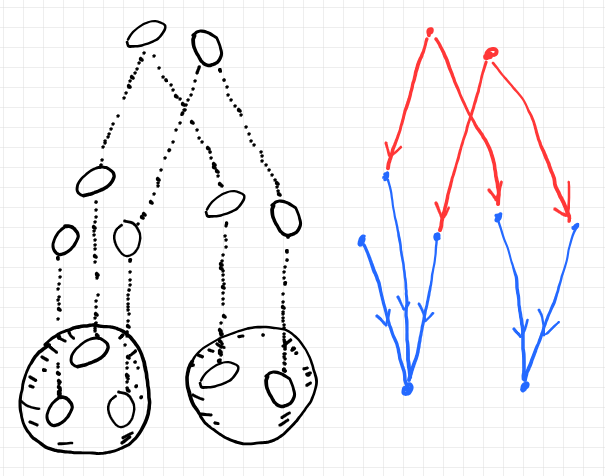
上図は、3つの穴(「ドーナツの穴」ではなくて「靴下の穴」のほう)があいた球面と、2つの穴があいた球面を、境界(の一部)で貼り合わせる方法を指示する図です。左側は少しリアル(下手くそでリアリティあまりないですが)に描いています。右側は貼り合わせ図式の形状グラフです。青い部分が境界図式で、赤い部分が境界図式とアタッチされたマッチング図式です。マッチング図式は、2つのマッチャー・スパンからなり、スパンはどちらも2本脚(つまり非特異マッチャー)です。
この“貼り合わせ方の指示”に従って実際に貼り合わせを行うと下図のようになります。
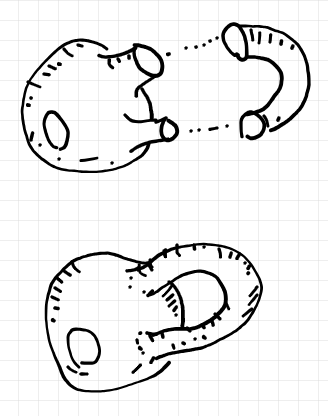
スムーズに*4貼り合わせが行えるように、穴の境界を突き出すように変形します。2つ穴の球面はパイプの形にしています。境界で貼り合わせを行うと、穴が1つあいた把手〈とって | ハンドル〉が付いた球面になります。
貼り合わせ操作は、多様体の同型類のあいだの演算とみなしているので、同型である範囲内での具体的な形状の違いは無視して考えます。例えば、2つ穴の球面とパイプの違いは無視します。
貼り合わせ演算
圏 $`\cat{C}`$ に対して、同型射〈可逆射〉だけからなる広い部分圏を $`\cat{C}^\mrm{iso}`$ 、$`\mrm{Iso}(\cat{C})`$ 、$`\mrm{Core}(\cat{C})`$ などと書きます。が、$`\mrm{Iso}({\bf KMan}^{\le 2})`$ は煩雑なので、名前の語尾に G を足して $`{\bf KManG}^{\le 2}`$ という記号を使います。G は groupoid からです。
これから、亜群 $`{\bf KManG}^{\le 2}`$ 上の貼り合わせ演算を定義します。貼り合わせ演算とは、貼り合わせ図式に対する余極限のことです。本質的には余極限ですが、使い勝手がいいように周辺を整備します。
一般に、亜群上の前層をスピシーズ〈species〉と呼び*5、前層の圏をスピシーズの圏〈category of species〉*6と呼びます。亜群上だと前層と余前層の区別は曖昧になるので、余前層/余前層の圏をスピシーズ/スピシーズの圏と呼ぶこともあります。どっちでもかまいません。ここでは、$`{^\mrm{op}}`$ を付ける手間を省くために(それだけの理由で)余前層を使うことにします。
$`M \mapsto \u{\mrm{GluD}}[M]`$ は、$`{\bf KMan}^{\le 2}`$ 上の関手にはなりませんが、亜群 $`{\bf KManG}^{\le 2}`$ 上では集合値関手、つまりスピシーズになります。
$`\quad \u{\mrm{GluD}}[\hyp] : {\bf KManG}^{\le 2} \to {\bf Set} \In {\bf CAT}`$
$`{\bf KMan}^{\le 2}`$ の対象の同型分類は知られています。つまり、同型類の集合 $`|{\bf KMan}^{\le 2}|/\!\cong`$ はハッキリしており小さな集合です。次のように置きます。語尾の C は class のつもりです。
$`\quad \u{\mrm{KManC}}^{\le 2} := |{\bf KMan}^{\le 2}|/\!\cong \:\in |{\bf Set}|`$
$`M \mapsto \u{\mrm{KManC}}^{\le 2}`$ という定数関手もスピシーズになります。記号の乱用で次のように書きます(定数値と関手をオーバーロードします)。
$`\quad \u{\mrm{KManC}}^{\le 2} : {\bf KManG}^{\le 2} \to {\bf Set} \In {\bf CAT}`$
スピシーズのあいだの射とは、余前層のあいだの自然変換です。$`\alpha`$ が上記の2つのスピシーズのあいだの自然変換なら、$`\alpha`$ は次のような成分の集まりです。
$`\text{For }M \in |{\bf KManG}^{\le 2}|\\
\quad \alpha_M : \u{\mrm{GluD}}[M] \to \u{\mrm{KManC}}^{\le 2} \In {\bf Set}
`$
自然性四角形は次のようになります。
$`\text{For }f: M \to N \In {\bf KManG}^{\le 2}\\
\quad \begin{CD}
\u{\mrm{GluD}}[M] @>{\alpha_M}>> \u{\mrm{KManC}}^{\le 2} \\
@V{\u{\mrm{GluD}}[f]}VV @| \\
\u{\mrm{GluD}}[N] @>{\alpha_N}>> \u{\mrm{KManC}}^{\le 2} \\
\end{CD}\\
\quad \text{commutative }\In {\bf Set}
`$
成分写像 $`\alpha_M`$ が、$`M`$ 上の貼り合わせ図式に対する余極限(の同型類)で与えられるとき、そのようなスピシーズ射を貼り合わせ演算〈gluing operation〉と呼びます。以下の $`[m], [\mrm{colim}\,m]`$ のブラケットは同型同値類を表すブラケットです。
$`\text{For }m \in \mrm{GluD}[M]\\
\quad \alpha_M ( [m]) := [\mrm{colim}\, m] \; \in \u{\mrm{KManC}}^{\le 2}
`$
貼り合わせ演算をうまく定義するには幾つかの問題があります。それを次節で指摘します。
貼り合わせ演算の構成
前節の貼り合わせ演算の定義は、「もしこういう演算があるならば、それを貼り合わせ演算と呼ぶ」というスタイルのもので、亜群 $`{\bf KManG}^{\le 2}`$ 上に実際に貼り合わせ演算が存在することを保証するものではありません。実際、余極限が存在しない貼り合わせ図式があります。
貼り合わせ演算をうまく構成する方法は幾つかあります。ひとつの方法は、貼り合わせ図式を制限することです。例えば、非特異な貼り合わせ図式だけに制限すると、任意の(非特異な)貼り合わせ図式に余極限が存在します。
別な方法として、スピシーズの値の圏(ターゲット圏)を集合圏から部分関数の圏に置き換えることです。スピシーズのあいだの射の成分は部分関数になります。
$`\text{For }M \in |{\bf KManG}^{\le 2}|\\
\quad \alpha_M : \u{\mrm{GluD}}[M] \to \u{\mrm{KManC}}^{\le 2} \In {\bf Partial}
`$
貼り合わせの結果(余極限対象)が存在しないことを許容するので、一部未定義かも知れない貼り合わせ演算が定義可能です。
最初の貼り合わせ図式を制限する方法は、部分関数の族として定義された貼り合わせ演算が全域となるように、うまく部分スピシーズ(部分集合の集まり)を選ぶことだとも言えます。
また別な方法は、貼り合わせ図式の集まり(複雑な構造を持つ)を作る操作をモナドに仕立てることです。この方法はこの記事の最後で触れています。貼り合わせ演算は、モナドのアイレンベルク/ムーア代数の演算となります。モナドの自由代数〈クライスリ代数〉は貼り合わせ演算を備えた(亜群/スピシーズを台とする)代数系になります。
いずれの方法を使ったにしても、亜群 $`{\bf KManG}^{\le 2}`$ 上のスピシーズのあいだの射として定義された貼り合わせ演算(余極限の族)が定義できた場合、「亜群、スピシーズ、貼り合わせ演算」一式を貼り合わせ代数〈gluing algebra〉と呼びます。
貼り合わせ代数の主役は貼り合わせ演算です。ベースの亜群が $`{\bf KManG}^{\le 2}`$ の場合、スピシーズ $`\u{\mrm{GluD}}[\hyp]`$ が貼り合わせ演算の“引数の型”を提供し、定数値スピシーズ $`\u{\mrm{KManC}}^{\le 2}`$ が“戻り値の型”を提供します。亜群の射は“アルファ変換”(リネーミング、リラベリング)に相当します。
一般的貼り合わせ代数
具体的な圏である $`{\bf KMan}^{\le 2}`$ の代わりに、一般的・抽象的な圏 $`\cat{C}`$ から出発して貼り合わせ代数を構成できないでしょうか? 貼り合わせ代数の公理的な定義を探る、ということです。
まず、圏 $`\cat{C}`$ は、余デカルト・モノイド積を持つとします。記号の乱用で次のように書きます。
$`\quad \cat{C} = (\cat{C}, +, 0) \;\in |{\bf SymMonCAT}|`$
$`\cat{C}`$ の図式の圏 $`\mrm{Diag}^{\bf FG}(\cat{C})`$ は特に問題なく構成できます。多様体の圏と同様な議論で、演算 $`\BoxSum`$ 、 $`\BoxCSum{i}{A}{j}`$ も定義できます。特に、図式の圏を対称モノイド圏にできます。
$`\quad \mrm{Diag}^{\bf FG}(\cat{C}) = (\mrm{Diag}^{\bf FG}(\cat{C}), \BoxSum, \u{0}) \;\in |{\bf SymMonCAT}|`$
部分圏 $`\cat{C}_\mrm{conn}`$ と $`\cat{C}_\mrm{border}`$ は公理的に要請します。
$`\quad \cat{C}_\mrm{border} \subseteq \cat{C}_\mrm{conn} \subseteq \cat{C} \In {\bf CAT}`$
$`\cat{C}_\mrm{conn}`$ の対象はすべてモノイド原子的だとします(「原子射と末端射」参照)。また、部分圏 $`\cat{C}_\mrm{conn}`$ は生成的だとします -- これは、$`\cat{C}_\mrm{conn}`$ を含む最小の対称モノイド圏が $`\cat{C}`$ と一致することです*7。
$`\cat{C}`$ の対象に連結成分の集合を対応させて、射に連結成分のあいだの写像を対応させる関手も公理的に要請します。
$`\quad \mrm{CC} :\cat{C} \to {\bf FinSet} \In {\bf CAT}`$
$`\cat{C}_\mrm{conn}`$ が原子的モノイド生成系になっていることから、任意の対象 $`M\in |\cat{C}|`$ は次のように分解できます。
$`\quad M \cong \sum_{i \in \mrm{CC}(M)}C_i \text{ where }C_i \in |\cat{C}_\mrm{conn}|`$
$`\cat{C}`$ の対象に境界図式を対応させる関手も公理的に要請します。
$`\quad \bdryD : \cat{C} \to \mrm{Diag}^{\bf FG}(\cat{C}) \In {\bf SymMonCAT}`$
具体的な圏 $`{\bf KMan}^{\le 2}`$ の場合を模倣して、亜群 $`\cat{C}^\mrm{iso}`$ 上のスピシーズを定義できます。
- $`|\cat{C}^\mrm{iso}| \ni M \mapsto \u{\mrm{GluD}}[M] \;\in |{\bf Set}|`$
- $`|\cat{C}^\mrm{iso}| \ni M \mapsto \u{|\cat{C}|}\;\in |{\bf Set}|`$、ここで $`\u{|\cat{C}|} := |\cat{C}|/\!\cong`$
以上のセットアップのもとで、貼り合わせ演算を載せれば、一般的貼り合わせ代数を定義できるでしょう。
おわりに
貼り合わせ代数の公理的な定義はまだ中途半端です。二段階に分けて定義するのがよさそうです。
- 対称モノイド圏 $`(\cat{C}, +, 0)`$ と、原子的モノイド生成系となっている部分圏 $`\cat{C}_\mrm{conn}`$ により構成される構造
- さらに、ボーダー対象の部分圏 $`\cat{C}_\mrm{border} \subseteq \cat{C}_\mrm{con}`$ と、境界図式関手 $`\bdryD`$ で構成される構造
台となる圏 $`\cat{C}`$ は最初から亜群に限定してもいいかも知れません(そのほうが話が簡単)。([追記]最初から亜群はうまくないようです。中心となるのは亜群ですが、補助的に亜群ではない圏も使います。[/追記]
上記の構造を、大幅な省略と記号の乱用で $`\cat{C} = (\cat{C}, \bdryD)`$ と表すとして、貼り合わせ図式を対象とする圏 $`\mrm{GluD}(\cat{C})`$ を構成します。$`\mrm{GluD}(\hyp)`$ をモナドに仕立てることができて、貼り合わせ代数はそのモナドのアイレンベルク/ムーア代数として定義できたらいいな、と思っています。
貼り合わせ代数には多くの例があります。冒頭に挙げたダンクソ/ハラーチェバ/ロバーツォンのワイヤリング図のオペラッド、コステロの半グラフの圏、ボリソフ/マニンの半グラフの圏は貼り合わせ代数の事例となるはずです。
*1:ピクチャーパズルとよく似ています。パズルのピースは、絵の断片が描かれた小さなキャンバスです。
*2:ゼロ同境〈null-cobordant〉な多様体ともいいます。
*3:空グラフや空多様体を $`0`$ と書いて、そこからの唯一の射を $`\u{0}`$ と書きましたが、この下線は商集合とは別な用法です。
*4:“可微分的に”という意味もあります。
*5:ジョイアル〈André Joyal〉のオリジナルの定義では、亜群として有限集合と同型写像の亜群を使います。
*6:species は、単数形も複数形も species です
*7:本質的に一致するでもかまいません -- これは、包含関手の本質像〈essential image〉が全体圏 $`\cat{C}`$ になることです。