マックレーンの五角形をインデックスなしの等式で表す - 檜山正幸のキマイラ飼育記 (はてなBlog)

モノイド圏の定義でマックレーンの五角形と三角形が出てきます。最初は何だか意味不明なんですが、マックレーンの五角形／三角形の可換図式は、モノイド圏の肝のひとつです。これらの可換図式をインデックス（パラメータ、全称限量子の束縛変数）なしの等式で表してみます。

なんでそんなことをするかは最後の節でちょっと触れます。

内容：

マックレーンの五角形
色々な描き方
ツリーの変形としての五角形
記法の工夫をしないと
2次元の等式的定義

マックレーンの五角形

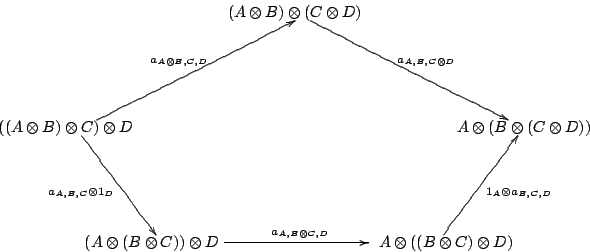
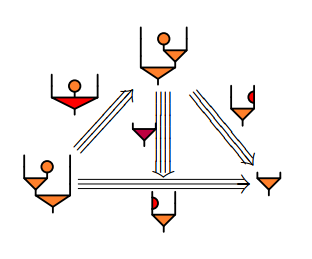
マックレーンの五角形と三角形の可換図式は次のようなものです。

*1
*2

五角形の上側の二辺を時計回りにたどると：

α_A⊗B,C,D
α_A,B,C⊗D

五角形の下側の三辺を反時計回りにたどると：

α_A,B,C $\otimes$ id_D
α_A,B⊗C,D
id_A $\otimes$ α_B,C,d

モノイド圏をCとして、Cの射の図式順結合を';'で表せば、五角形可換図式は次のような等式になります。左辺が上側時計回り、右辺が下側反時計回りです。

α_A⊗B,C,D ; α_A,B,C⊗D = α_A,B,C $\otimes$ id_D ; α_A,B⊗C,D ; id_A $\otimes$ α_B,C,D

この等式では、自然変換αの成分表示を使っています。A, B, C, DはCの任意の対象なので、実際には次のように全称限量子が等式の先頭に付きます。

∀A, B, C, D∈|C|.( α_A⊗B,C,D ; α_A,B,C⊗D = α_A,B,C $\otimes$ id_D ; α_A,B⊗C,D ; id_A $\otimes$ α_B,C,D )

限量子もインデックス（成分表示における下付きの対象）もなしで五角形を等式表示できないでしょうか。この問〈とい〉がこの記事の主題ですが、次節では絵の話をします。

色々な描き方

マックレーンの五角形／三角形は手書きで何度か描いたことがあります。

2月の圏論勉強会 - 檜山正幸のキマイラ飼育記（五角形の上側は反時計回り、五角形の下側は時計回り）

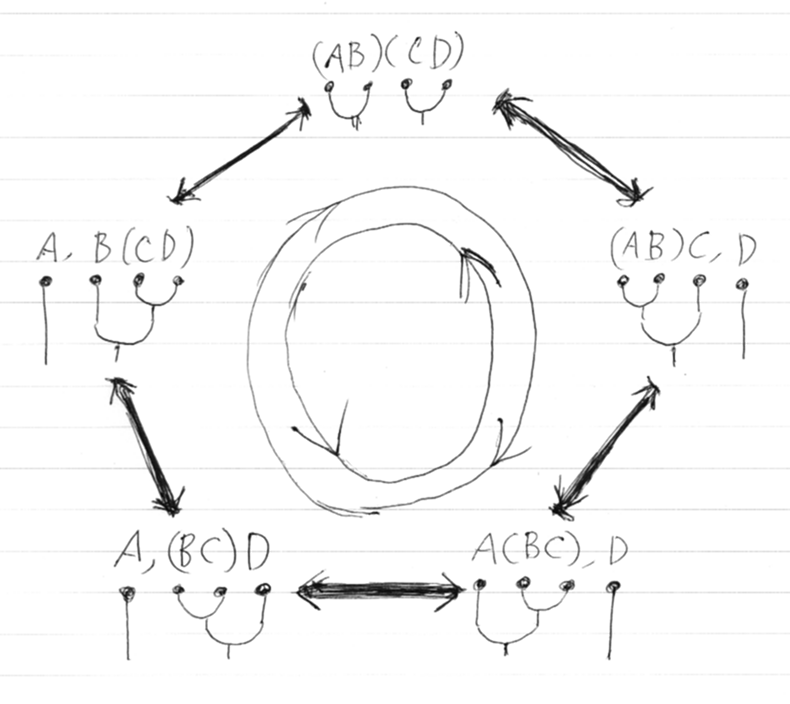
マックレーンの五角形の絵 - 檜山正幸のキマイラ飼育記（五角形の上側は反時計回り、五角形の下側は時計回り）

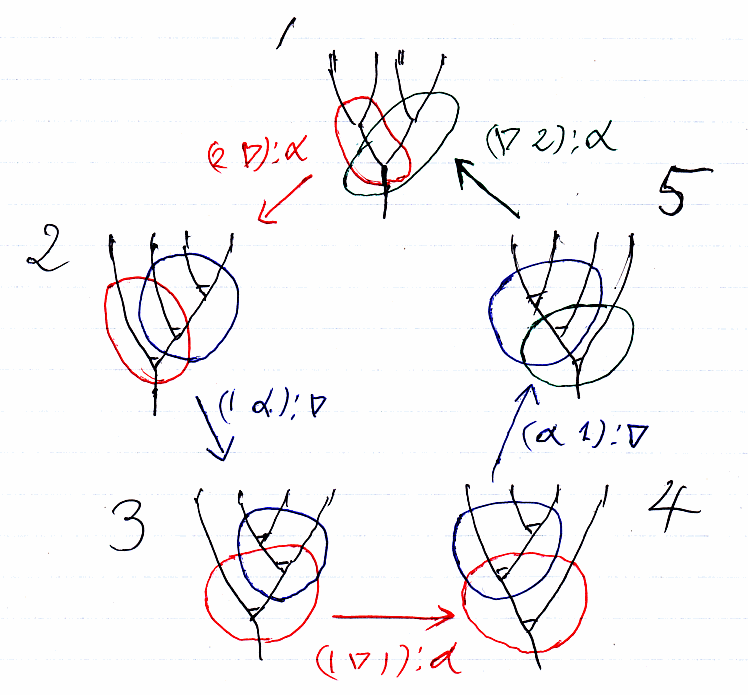
モノイド圏と加群圏に関するフォークロアとマックレーン五角形・三角形（五角形の上側は時計回り、五角形の下側は反時計回り）

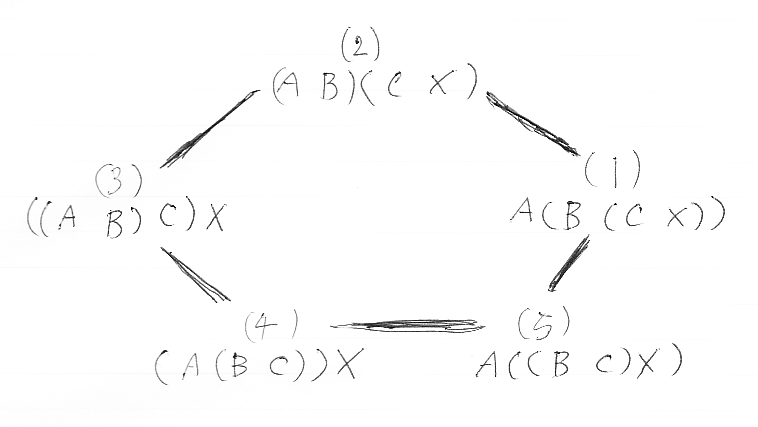
これらの図で、五角形の頂点はツリーで、五角形の辺はツリーの変形になっていることが分かるでしょう。ストリート（Ross Street）は、ツリーの代わりに五角形を使って、“五角形を頂点に描いた五角形”を使ったりしています（珍しい描き方です）。

ギロー／マルボス（Yves Guiraud, Philippe Malbos）のスライドには、綺麗な五角形の絵があります。ただし、この絵では、五角形の辺が3-射（3次元の射）で、五角形全体が表す射は4-射になっています。我々が扱う状況は次元が1つ下がって、五角形の辺が2-射で、五角形全体は3-射です。

ツリーの変形としての五角形

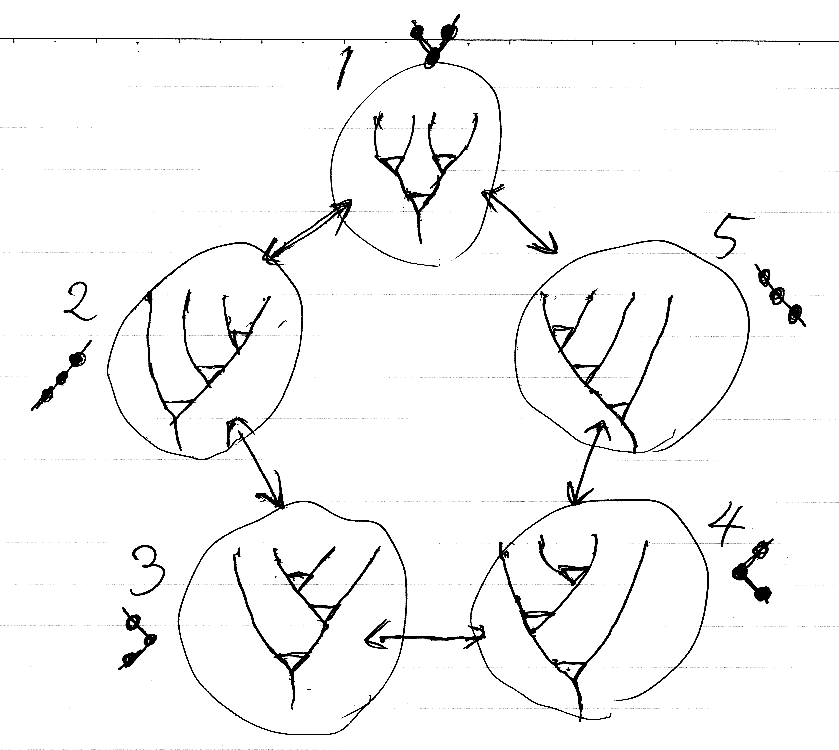
さて、五角形をツリーの変形過程の絵として捉えましょう。次の図を使うことにします。冒頭の可換図式と同じレイアウトにツリーの絵を足したものです。

豊饒圏をちゃんと定義したい - 檜山正幸のキマイラ飼育記（五角形の上側は時計回り、五角形の下側は反時計回り）

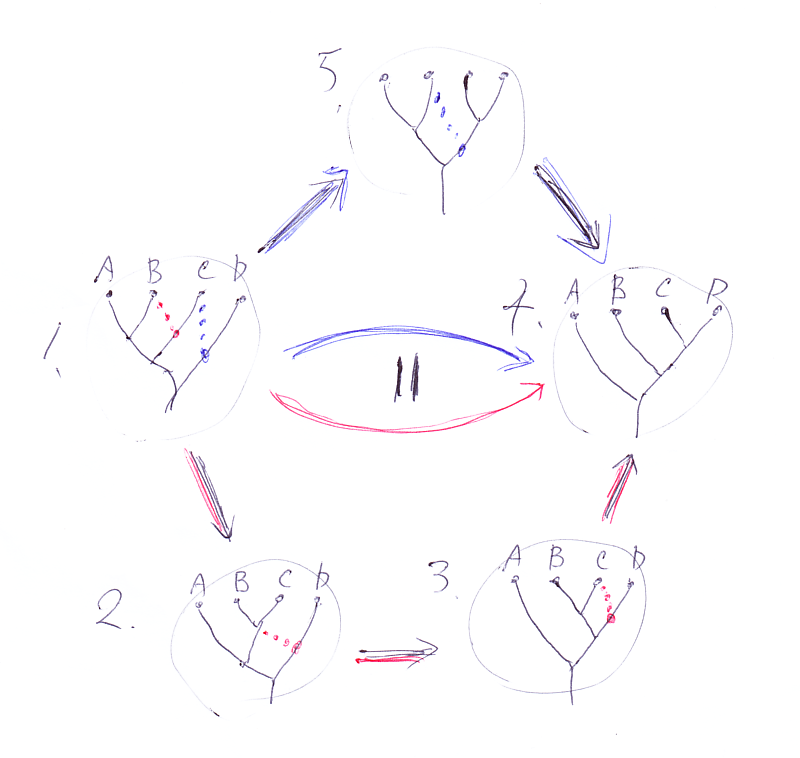
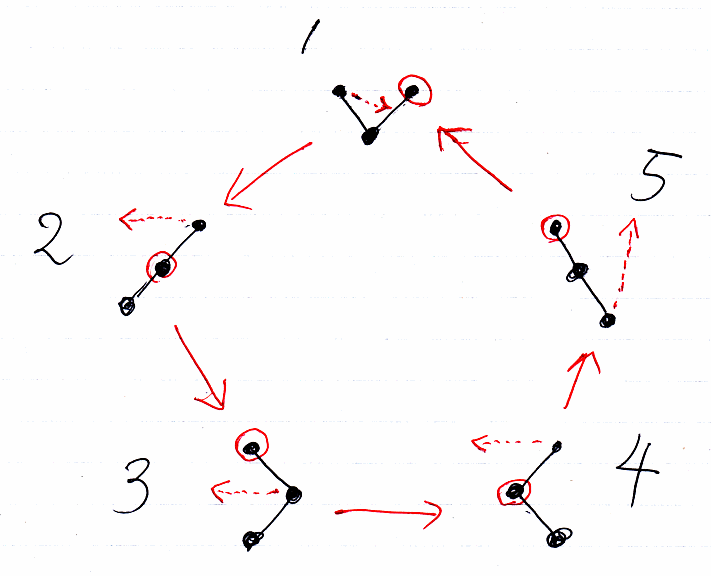
この図の上側の時計回り（青い矢印 1→5→4）の変形をアスキーアートで描いてみます。

Y I I     Y Y     | | Y
 Y |  ==>  Y  ==>  | Y
  Y                 Y

これを、“絵”ではなくて“式”として合理化します。

圏Cの恒等関手 Id_C:C→C をIと書くことにする。I:C→C （IはCの単位対象ではないので注意）
圏Cのモノイド積 $\otimes$ :C×C→C をYと書くことにする。Y:C×C→C
圏の直積、関手の直積を併置（空白を挟んでもよい）で表す。例えば、Id_C×Id_C×Id_C = III = I I I 、 $\otimes$ ×Id_C = YI = Y I 。
関手の図式順結合を'*'で表す。
関手の結合（アスタリスク）より直積（併置）のほうが演算子の優先度が高いとする。

以上の約束で、上のアスキーアートの左のツリーは、YII*YI*Y と書けます。縦にスタックする代わりにアスタリスク'*'を使います。上から下へのスタックが、アスタリスクをはさんだ左から右への1行でテキスト表示されます。

結合律子α（律子に関しては「律子からカタストロフへ」を参照）は、次のように書けます。

α:: YI*Y⇒IY*Y : CCC→C

これを反図式順（'・'は右から左に読む）の普通の記法で書くと：

α:: $\otimes$ ・( $\otimes$ ×Id_C)⇒ $\otimes$ ・(Id_C× $\otimes$ ) : C×C×C→C

見てのとおり煩雑になるし、ツリーとの対応も取れなくなるので、この記法は使いません。

α::YI*Y⇒IY*Y を YII*YI*Yの下側のYI*Yに適用すれば次のようになります。

Y I I     Y | |
 Y I  ==>  I Y
  Y         Y

この変形を YII*α と書きます。これは関手YIIと自然変換αのヒゲ結合〈whiskering〉です。ヒゲ結合も自然変換の横結合も通常同じ演算子記号（ここでは'*'）で表します。

直積はモノイド積なので、交替律〈interchange law〉 FG*F'G' = (F*F')(G*G') があります。交替律を使うと、次のツリーはいずれも同じ関手を表します。グラフとして同じトポロジーなら同じ関手です。

Y | |   Y Y   Y Y   | | Y
 I Y    | |    Y     Y |
  Y      Y            Y

上の一番右のツリーの下側のYI*Yに α::YI*Y⇒IY*Y を適用すると、

I I Y     I I Y
 Y I  ==>  I Y
  Y         Y

この変形は、関手IIYと自然変換αのヒゲ結合ですから IIY*αと書けます。

今説明した2つの変形を繋げると五角形の上側になるので、YII*α ; IIY*α が以下の変形です。

Y I I        I I Y
 Y I  ==>==>  I Y
  Y            Y

同じ要領で五角形の下側もたどると、それぞれの変形は次のように表せます。

α(I*I)*Y = αI*Y （I*I = I なので）
IYI*α
(I*I)α*Y = Iα*Y

繋げれば、

αI*Y ; IYI*α ; Iα*Y

ですね。

したがって、五角形が表す等式は、

YII*α ; IIY*α = αI*Y ; IYI*α ; Iα*Y

となります。

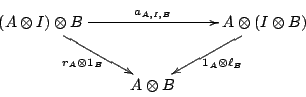
この記事では、マックレーンの三角形のほうには焦点を当ててませんが、同様にして次の等式が得られます。

IiI*α = ρI*Y ; Iλ*Y

ここで：

1は、ひとつの対象と恒等射からなる自明な圏
i:1→C は、単位対象を特定するポインティング関手
λ::iI⇒I:C→C は、左単位律子
ρ::Ii⇒I:C→C は、右単位律子

記法の工夫をしないと

次の表は、「関手と自然変換の計算に出てくる演算子記号とか」で出した表の抜粋（に直積を追加）したものです。

演算	反図式順演算子記号	図式順演算子記号
圏／関手の直積	×	併置
関手の結合	・	*
自然変換の縦結合	$\circ$	;
関手と自然変換のヒゲ結合	・	*
自然変換の横結合	・	*

特に工夫をしない反図式順で前節の等式（下に再掲）を書き下してみましょう。

YII*α ; IIY*α = αI*Y ; IYI*α ; Iα*Y

部分ごとに翻訳します。

左辺の右 [α・(Id_C×Id_C× $\otimes$ )]
左辺の左 [α・( $\otimes$ ×Id_C×Id_C)]
右辺の右 [ $\otimes$ ・(Id_C×α)]
右辺の中 [α・(Id_C× $\otimes$ ×Id_C)]
右辺の左 [ $\otimes$ ・(α×Id_C)]

これらを組み合わせると：

[α・(Id_C×Id_C× $\otimes$ )] $\circ$ [α・( $\otimes$ ×Id_C×Id_C)] = [ $\otimes$ ・(Id_C×α)] $\circ$ [α・(Id_C× $\otimes$ ×Id_C)] $\circ$ [ $\otimes$ ・(α×Id_C)]

煩雑で図式的直感も働かなくて、何もいいことがないのですが、現状のメジャーな記法は反図式順記法です*6。

2次元の等式的定義

「マイクロコスモ原理の恐怖」で、マイクロコスモ原理について紹介しました。

https://ncatlab.org/nlab/show/microcosm+principle

Microcosm principle: Certain algebraic structures can be defined in any category equipped with a categorified version of the same structure.
マイクロコスモ原理： 特定の代数構造は、その代数構造を圏化した構造を備える圏のなかで定義可能である。

ある代数構造を定義したいとき、それを定義する環境にも類似の構造が要求される、ということです。マイクロコスモ原理の典型例は、モノイドを定義するための環境としてモノイド圏が要求されることです。

では、モノイド圏を定義する環境にはいかなる構造が要求されるのでしょう。このことを調べるために、モノイド圏の定義の一部であるマックレーンの五角形／三角形を等式的に記述したかったのです*7。

サイズの問題を避けるために、Cは小さなモノイド圏だとします。すると、Cは小さい圏の圏Cat内で定義されます。Catは直積を持つ厳密2-圏で、演算として、直積／縦結合／横結合を持ちます。

射の次元	直積 ×	縦結合 ;	横結合 *
0-射＝圏	圏の直積	-	-
1-射＝関手	関手の直積	関手の結合	-
2-射＝自然変換	自然変換の直積	自然変換の縦結合	自然変換の横結合

Catのなかで、モノイド圏Cが定義される様〈さま〉を観察しましょう。モノイド圏を構成する素材を列挙します。素材は、上の表に書いた各次元の射（0-射, 1-射, 2-射, 3-射）です。3-射は、実は等式です。

0-morphism C
1-morphism I: C→C （I = Id_C）
1-morphism Y: CC→C
1-morphism i: 1→C
2-morphism α:: YI*Y⇒IY*Y : CCC→C
2-morphism λ:: iI*Y⇒I : C→C
2-morphism ρ:: Ii*Y⇒I : C→C
3-morphism penta::: YII*α ; IIY*α ≡> αI*Y ; IYI*α ; Iα*Y :: YII*YI*Y ⇒ IIY*IY*Y : CCCC → C
3-morphism tri::: IiI*α ≡> ρI*Y ; Iλ*Y :: IiI*YI*Y⇒Y : CC→C

2-圏における3-射が等式になることは、以下の記事に書いてある(-1)次元の圏と反転原理から言えます。

1-圏（単なる圏）における2-射である等式を使った定義は等式的定義ですが、これは1次元までの素材（生成射）に関する等式なので1-等式的定義と呼びます。モノイド圏の定義は、2次元までの素材に関する等式なので2-等式的定義〈2-equational definition〉となります。

マイクロコスモ原理に話を戻すと、具体的な“直積を持つ厳密2-圏”Cat内で、2-等式的定義としてモノイド圏の定義が得られたのでここでオシマイと考えることもできます。しかし、モノイド圏を定義する環境としての“直積（あるいは一般のモノイド積）を持つ厳密2-圏”を定義する環境は何か？と考えると、マイクロコスモ原理による梯子をさらに上に昇ることになります。この梯子をどこまで昇ればいいんだろう？という不安な感じが“マイクロコスモ原理の恐怖”です。

この恐怖感を払拭するひとつの手段は「抽象化をやめる」ことなのかも知れません。しかし、抽象化をしたい欲求もあります。現状、うまく折り合いが付いてません。[追記]ある程度の折り合いが付きました。→「デカルト構造の無限タワー：怖がらずに登れ」[/追記]

*1:画像を含む元記事： http://math.ucr.edu/home/baez/quantum/node4.html

*2:画像を含む元記事： http://math.ucr.edu/home/baez/quantum/node4.html

*3:画像を含む元記事： https://www.sciencedirect.com/science/article/pii/002240498790137X

*4:画像を含む元記事： https://www.irif.fr/~guiraud/exposes/tianjin.pdf

*5:画像を含む元記事： https://www.irif.fr/~guiraud/exposes/tianjin.pdf

*6:表記法と描画法の混乱ぶりは「絵算（ストリング図）における池袋駅問題の真相」を参照。

*7:等式的記述をしたい理由は他にもありますが。