このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

なぜ「光が影を作ること」と「主張の一部を再主張すること」が関係するのか；あるいは、デカルト圏入門

雑記／備忘

「1+1ができない子と線形論理」のコメント欄で田辺さんから質問をいただきました。よい質問だと思いますが、それに答えるのはけっこう手間がかかります。ですが、この際（どの際？）だから、ある程度は納得していただけるような説明を試みてみましょう。

[追記 date="翌日"]細かい修正をしました。[/追記]

今回も、プログラミング課題とプログラミングではない課題（「考える課題」と表記）を入れています。課題番号は全部通しでふってあります。課題をやらなくても差し障りはありませんが、問題文に目を通すことはしてください。あなたのお好みのプログラミング言語が、総称機構（型パラメータ）／自動型推論、高階関数をサポートしてないなら、適当な代替手段や手抜き法を工夫してください。


檜山の発言（要旨）：

タプル（ペア）の第1成分を取り出す射影という操作 (A, B) → A の、論理における類似物は、仮定A∧B（AかつB）からAを導く操作です。

田辺さんの質問：

A ∧ B → A が成り立つか否かは射影とは別概念と思いますが、射影という捉え方があるのでしょうか。


※印刷のときはサイドバーが消えます。
内容：

  1. 射影とは何か
  2. 直積と射影の性質
  3. デカルト圏の定義
  4. デカルト圏の実例
  5. 息切れしました、が、この先どうなっているかつうと

●射影とは何か

2つの集合AとBに対して、a∈A、b∈Bから作った(a, b)のようなタプル（主にペアを扱いますが）をすべて寄せ集めた集合をA×Bと書いて、AとBの直積（またはデカルト積）と呼びます（より詳しくは「タプルと直積」を参照）。

AもBも実数直線R（固有名詞は太字で書くのが習慣）だとすると、直積A×B=R×R=R2は、普通に座標が入った平面ですね。平面の点(x, y)に、そのx座標を対応させる写像（関数）を考えると、それは、真上からふりそそぐ太陽光線が地面（x軸上）に影を落とすことだと思えます。単一の点では雰囲気が出ないかもしれないので、平面になにか図形を描いて、x軸への影を考えてください。

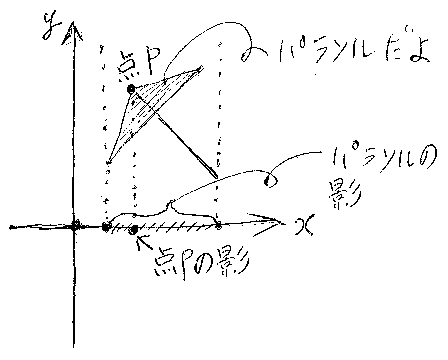
もっとも、この比喩には弱点があって、x軸の下にある図形の影を作るには、地下から上に向かって太陽光線を照射しなくてはなりません。ほんとは、影が落ちる場所はx軸じゃなくて、平面の外にある別な直線だと考えるべきなんです。

まー、いずれにしても、(x, y)|→x として定義される写像を射影といいます。(x, y)|→y も（水平方向に照射される光線による）射影です。より一般には、集合A、Bと直積A×Bに対して、A×B→A; (a, b)|→a を第1射影（first projection）、A×B→B; (a, b)|→b を第2射影（second projection）と呼びます。

  • 考える課題 1： 平面の点は第1射影（x座標）と第2射影（y座標）から完全に特定・再現できます。では、平面内の図形（集合R2の、“タチの良い”部分集合）Sは、その第1射影像（(x, y)∈S に対するxの全体）と第2射影像（(x, y)∈S に対するyの全体）から特定・再現できるでしょうか？
  • 考える課題 2： 前問の答はNO（できるとは限らない）です。では、第1射影像と第2射影像から完全に特定・再現できる図形はどんな図形でしょう？
  • 考える課題 3： 平面内の図形Sに対して、その第1射影像と第2射影像からSを再現できるとは限りませんが、“近似的には再現できる”と言えます。どのような意味で近似なのでしょう？
  • 自由に考える課題 4： 前問の近似を精密化する方法をいろいろ考えてください。「近似」や「精密化」の解釈は自由です。

●直積と射影の性質

以下、直積A×Bに対して、その第1射影 A×B→A をp1、第2射影 A×B→B をp2で表します。具体的には、

  • p1(a, b) = a （a∈A、b∈B）
  • p2(a, b) = b （a∈A、b∈B）

ホントは、p1, p2の引数は1つなので、タプルを作る丸括弧と引数を囲む丸括弧*1を両方とも律儀に書けば：

  • p1((a, b)) = a
  • p2((a, b)) = b

ですが、単一タプル引数と複数の引数をあまり区別しないので、ヨロシク。

  • 考える課題 5： A={0}、B={1, 2, 3}のとき、A×Bとp1, p2を具体的に書き下してください。
  • 考える課題 6： A={}（空集合）、B={1, 2, 3}のとき、A×Bとp1, p2はどうなるでしょう。
  • 考える課題 7： 項目の型がAであるリストの型（総称型）をList<A>、ノード（のラベル）の型がAであるツリーの型をTree<A>とします。ルートノード（のラベル）を取り出す関数をroot、子ノードリストを取り出す関数をchildrenとします。型を集合とみなして、直積A×List<Tree<A>> を考えると、この直積が再びTree<A>に対応し、第1射影がrootに対応し、第2射影がchildrenに対応することを確認してください。
  • プログラミング課題 8： 前問の状況を納得するため、ツリーノードを、ノードラベルと子ノードリスト（への参照）からなるタプル（ペア）で実装するプログラムを書いてください。もちろん、root、children はタプルの成分取り出し演算で実装します。root、childrenは、型パラメータを持つ総称関数*2で、root<A>:Tree<A>→A、children<A>:Tree<A>→List<Tree<A>>です。
  • 考える課題 9： ツリーが直積で表現できることには、多少の違和感をおぼえます（主観的な話だけど）。それはおそらく、再帰構造を含んでいるからでしょう。ツリーの再帰構造を明白にするため、BNFまたは再帰方程式でツリーを定義してください。
  • プログラミング課題 10： 正の数aは前もって与えられた定数として、連立方程式 {x = a*y, y = 1 + x*y, x, yは非負}を近似的に解くプログラムを書いてください。（次の問題も見ておいてね。）
  • 考える課題 11： なぜ、近似的な数値解法の問題がここに紛れ込んでいるのでしょう？（ヒント→「データ型のクレイジー計算」）

さて、次の図を眺めながら、後に続く説明を読んでくださいね。（下側の図で、「∈A×B」を書き忘れたけど、まー、いいや。）

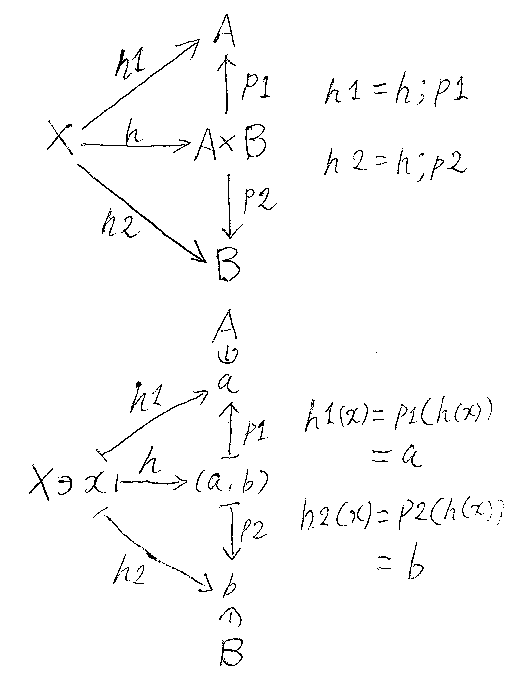
写像h:X→A×Bがあると、hに2つの射影p1とp2を後結合（post compose）して、h;p1とh;p2を作れます。h(x) = (a, b) と置くならば、

  • (h;p1)(x) = p1(h(x)) = p1(a, b) = a
  • (h;p2)(x) = p2(h(x)) = p2(a, b) = b

記法を単純にするため、h;p1 = h1, h;p2 = h2 と書くと：

  • h1(x) = a
  • h2(x) = b

ここで、最初の前提 h(x) = (a, b) を思い出すと次の等式が成立します。

  • h(x) = (h1(x), h2(x))

おおざっぱな書き方をするなら、h = (h1, h2) です。これは次のことを意味します。

  • 2つの射影p1, p2を使えば、集合Xから直積A×Bへの写像hを2つの“成分”に分けることができる。

第1成分h1と第2成分h2から、もとのhは完全に再現できます -- このことを述べるため、新しい記法を導入します。いまさっき、h = (h1, h2) と書きましたが、この記法は混乱を招くこともある*3ので、h = <h1, h2>と書くことにします。山形括弧（angular brackets）を使ったペア<f, g>の定義は、

  • <f, g>(x) = (f(x), g(x))

です。要素のペアには丸括弧、写像のペアには山形括弧と使い分けます。この記法で、「第1成分と第2成分からもとの写像を再現する」公式を書くと：

  • h = <h1, h2> = <h;p1, h:p2>

また、任意のf:X→A、g:X→Bから写像のペアリングにより組み立てられた h = <f, g>:X→A×B に関しては、

  • h1 = f、つまり <f, g>;p1 = f
  • h2 = g、つまり <f, g>;p2 = g

が成立します。

結局、「第1成分を取る＝第1射影を後結合」、「第2成分を取る＝第2射影を後結合」、「2つの写像をペアにする」という操作群により、写像の分解・合成が自由にできます。

  • 考える課題 12： tを時間変数（単位は秒でも分でもなんでもいいです）として、x座標／y座標を持つ平面内での等速直線運動を h:R(時間)→R×R(平面) とします。「h1 = h;p1 = 運動hの第1成分＝x座標の運動」、「h2 = h;p2 = 運動hの第2成分＝y座標の運動」とするとき、h1(t), h2(t)を具体的に書き下してください（初期位置、初速のパラメータを含みます）。
  • 考える課題 13： tを時間変数として、f(t) = cos(2πt), g(t) = sin(2πt) のとき、fとgのペアリング<f, g>:R(時間)→R×R(平面) は何を表すでしょう。
  • プログラミング課題 14： 直積概念をペア（成分が2つのタプル）として自前で実装しましょう。成分が型A、型Bであるペアの型をPair<A, B>とします。コンストラクタ pair<A, B>:A, B→Pair<A, B>、第1射影 proj1<A,B>:Pair<A, B>→A、第2射影 proj2<A, B>:Pair<A, B>→B をユーザー定義関数として書きましょう。
  • プログラミング課題 15： f:X→Aとg:X→Bから、fpair(f, g):X→Pair<A, B> を構成する高階関数 fpair<X, A, B>:Func<X, A>, Func<X, B>→Func<X, Pair<A, B>> を書いてください。また、fproj1<X, A, B>:Func<X, Pair<A, B>>→Func<X, A> と fproj2<X, A, B>:Func<X, Pair<A, B>>→Func<X, A> も書いてください。
  • プログラミング課題 16： 2つの関数をペアにしたデータであるPair<Func<X, A>, Func<X, B>>から、実際に動く関数Func<X, Pair<A, B>>を作り出す高階関数vitalize<X, A, B>:Pair<Func<X, A>, Func<X, B>>→Func<X, Pair<A, B>>と、その逆関数devitalize<X, A, B>を書いてください。
  • プログラミング／考える課題 17： 3つ組pair, proj1, proj2と、fの付いた3つ組fpair, fproj1, fproj2、それとvitalize, devitalizeの相互関係を考えてみましょう。
  • 自由にプログラミング／考える課題 18： 2引数関数と単一タプル（ペア）引数関数の違いが気になりませんか？ mproj1<A, B>:A, B→A、mproj2<A, B>:A, B→B （mはmulti-argumentのつもり）を定義して、pair, proj1, proj2との関係を考えてください。Pair<A, B>のペアを分解して、2つの成分を同時に返すには、“ホンモノ”の多値関数が必要ですね。さあ、多値について考えるときが来ました→多値関数

●デカルト圏の定義

前節で述べた「集合の直積」「2つの射影p1, p2」「写像のペアリング」についてまとめておきましょう。射影やペアリングは、実際には集合A, Bをパラメータとして持つので、ここではそれを明示することにします。ただし、小さい字のパラメータ（下付き添字）はウルサイのでたいていは省略します。括弧内は省略した形。

  1. 集合A、Bに対して、それらの直積A×Bが確定する。
  2. 2つの射影 p1A,B:A×B→A、p2A,B:A×B→B も確定する。
  3. 任意のf:X→A, g:X→B に対して、写像のペアリング<f, g>X,A,B:X→A×B が確定する。
  4. 任意のf:X→A, g:X→B に対して、<f, g>X,A,B;p1A,B = f 。（<f, g>;p1 = f）
  5. 任意のf:X→A, g:X→B に対して、<f, g>X,A,B;p2A,B = g 。（<f, g>;p2 = g）
  6. 任意のh:X→A×B に対して、<h;p1A,B, h;p2A,B>X,A,B = h 。（<h;p1, h;p2> = h ）

これをお手本にして、デカルト圏（cartesian categories）の定義を述べましょう。必要な圏論の知識は「はじめての圏論」の第3歩までです。前もって注意をいくつか：

  • A, Bなどは圏の対象です。集合とは限りません。
  • (-)×(-)（ナニカかけるナニカ）は、圏の対象に対して定義された二項演算です。集合の直積とは限りません。
  • f, gなどは圏の射です。写像とは限りません。
  • <(-), (-)>は、圏の射に対して定義された二項演算です。写像のペアリングとは限りません。
  • しかし、「わかりにくい」と感じたらすぐに、今までの集合の例に戻ってください。

さて、圏Cが、上記のような対象に対する二項演算(-)×(-)と、対象2つでパラメータ付けされた射の集まり p1A,B, p2A,B、対象3つでパラメータ付けされた射の二項演算の集まり <(-), (-)>X,A,Bを備えていて、次の等式を満たすとき、デカルト圏と呼びます。

  1. 任意のf:X→A, g:X→B に対して、<f, g>X,A,B;p1A,B = f 。（<f, g>;p1 = f）
  2. 任意のf:X→A, g:X→B に対して、<f, g>X,A,B;p2A,B = g 。（<f, g>;p2 = g）
  3. 任意のh:X→A×B に対して、<h;p1A,B, h;p2A,B>X,A,B = h 。（<h;p1, h;p2> = h ）

おっと、ひとつ忘れていました。Cには、特定された（distinguished/selected/chosen）対象Iも必要です。Iの特徴は：

  • Aが何であっても、A→Iという射がただ1つ存在する*4。

※注意：デカルト圏を、別なスタイルの定義で学んだ方もいるでしょう。どの定義でも実質的には同じです。ここで採用したスタイルは等式的（equational）な定義です。（参考になるかな？→「デカルト圏の等式的定義 細かいこと色々」）

なんか抽象的な定義でやんなっちゃうよなー。じゃ、実例いきましょう（次節）。もし、抽象的な定義をいじるのが得意であれば、次の問題をやってみてください（無理してやんなくてもいい）。

  • 考える課題 19： ただ1つ存在するA→Iという射を!Aと書くことにして（割と一般的な記法です）、idI = !I、f:A→Bに対して f;!B = !A を示してください。
  • 考える課題 20： 等号の両辺が定義できる状況で、「<f, g> = <u, v> ⇔ f = u かつ g = v」を示してください。
  • 考える課題 21： 等号の両辺が定義できる状況で、h;<f, g> = <h;f, h;g> を示してください。
  • 知っていれば考える課題 22： 双関手を知っているなら； f:A→B, g:C→D に対して f×g = <p1A,C;f, p2A,C;g> : A×C→B×D と定義します。すると、対象に対する×と射に対する×を一緒にしたものは、C上の双関手になることを示してください。

●デカルト圏の実例

集合と写像の圏に、集合の直積(-)×(-)、直積からの射影p1, p2、写像のペアリング<(-), (-)>を一緒に考えればもちろんデカルト圏です。すべての集合を考えると大きすぎると感じるなら、有限集合だけに限定してもデカルト圏です。

別な、もっと小規模な例を出しましょう。予備知識は、「はじめての圏論 その第3歩：極端な圏達」の“やせた圏”です。

0を含む自然数全体N = {0, 1, 2, ...}に、どの数よりも大きな無限大∞を加えた集合をNI = {0, 1, 2, ..., ∞}（N with Infinity）とします。NIには、0が最小で∞が最大となる普通の順序を考えます。NIは順序集合なので、自動的にやせた圏（実際にはとてもやせた圏）になります。

a, b∈NIとして、a→b という形の射があるのは、a≦b のときに限ります。

  • a→b という射がある ⇔ a≦b

aとbに対して、a→b の射はあっても唯一なので、それを[a, b]と書くことにしましょう（いちいち名前を付けなくて済む）。ただし、くどいけど、

  • 射[a, b]がある ⇔ a≦b

なので、[3, 1]とか[∞, 一兆の一億倍くらいデカイ数]とかは存在しません。以下、[a, b]と書いたらそれは a≦b を前提にしていることにします。

圏NIC（network interface cardでもNetwork Information Centerでもなくて、NIをもとにしたCategory）を、次のように定義します。

  1. Obj(NIC) = |NIC| = NI
  2. Morph(NIC) = NIC = {[a, b] | a, b∈NI ただし a≦b}
  3. dom([a, b]) = a、cod([a, b]) = b
  4. 対象aの恒等射は[a, a]、つまり ida = [a, a]
  5. 射[a, b]と[b, c]の結合は[a, c]、つまり、[a, b];[b, c] = [a, c]
  • 考える課題 22： NICが実際に圏になることを確認してください。

さーて、NICに、(-)×(-)、p1, p2, <(-), (-)> を導入します。まず、非常に混乱すると思うんだけど、a, b∈|NIC|に対して、a×b = min(a, b) = (a, bの大きくないほう) と定義します。記号「×」が掛け算じゃないのだよね。いきがかり上しょうがないのよー。十分に注意してね！ ちょっと練習しておくか。

  • やってみる課題 23： NICのなかで、0×3, 5×5, ∞×5, 100×10 を計算してください。

射影p1, p2と射のペアリング<(-), (-)>は次のように定義します。

  • a, b∈|NIC|に対して、p1a,b:a×b→a は [min(a, b), a]。p2a,b:a×b→a は [min(a, b), b]。
  • x, a, b∈|NIC|と、[x, a], [x, b]に対して、<[x, a], [x, b]>x,a,b:x→a×b は [x, min(a, b)]。

ま、とりあえず：

  • やってみる課題 24： NICのなかで、p10,3, p20,3, p1∞,5, p2∞,5を求めてください。
  • やってみる課題 25： NICのなかで、<[1, 2], [1, 3]>, <[100, ∞], [100, 100]>を求めてください。

NICってば、集合／写像、集合の直積とはえらく違った構造なんだけど、それでもデカルト圏です。

  • 考えてみる課題 26： p1a,b = [min(a, b), a]、p2a,b = [min(a, b), b]、<[x, a], [x, b]>x,a,b = [x, min(a, b)] がwell-definedなこと、つまり不等号の条件を満たしていることを確認してください。
  • 考えてみる課題 27： NICが（(-)×(-), p1, p2, <(-), (-)>と共に）デカルト圏であることを確認してください。忘れがちな（実際忘れていて後から追加した）Iは、∞です。

●息切れしました、が、この先どうなっているかつうと

デカルト圏を導入して、もう息切れした。 まーしかし、次のような筋道をたどってきたんだよね。

  1. 集合の直積と射影という概念を説明した。
  2. 直積や射影の性質を調べた。
  3. 直積や射影の性質を抽象化して、デカルト圏を定義した。
  4. そしたら、対象が集合の圏だけじゃなくて、NICみたいな小規模なデカルト圏の例も見つかった。

さてと、NIC以外にもデカルト圏はないのかいな？ ありますよ。“論理の代数”といわれているブール代数（Boolean algebras）やハイティング代数（Heyting algebras）も実はデカルト圏とみなせます。これらには、単なるデカルト圏以上の構造も入っていて、デカルト閉圏（cartesian closed categories）なんです。それで結局、古典論理（ブール代数）も直観論理（ハイティング代数）もデカルト閉圏の枠組みで扱うことが可能なわけ（「可能」なのであって、それが良いかどうかは別問題）。

古典／直観論理における A∧B |- A （A∧Bを仮定してAを演繹できる）とか、A∧B⊃A が正しい命題だとかの話は、ブール／ハイティング代数における対応する話に翻訳できます。それをデカルト閉圏の枠組みで眺めてやると、射影p1の性質に他ならない。と、そういうことです。

これで、太陽光線の影を比喩としてはじまったストーリーはいちおう完結です。ふー、疲れた。デカルト閉圏のもう少し詳しい話はいつか(?)するかもしれません（このテのバックログが溜まりすぎているから無理かも）。あ、それと、田辺さんのもう1つの質問への応答は、リソースの話としていつか(?)するかもしれません（なるべく早くしたほうがいいとは思いますが…）。

最後に：

  • 知っていれば考えてみる課題 28： （strictとは限らない）モノイド圏（monoidal categories）を知っているなら；「知っていれば考えてみる課題 22」で、デカルト圏Cの(-)×(-)が双関手となることはわかりました。さらに、(C, ×, I)が対称モノイド圏となることを示してください。対称σと、結合性、単位性を保証する自然同型α、λ、ρ（とそれらの逆）を定義して、σの公理や五角形／三角形等式を示さなくてはなりません。面倒です。

*1:「タプルと引数に、同じ丸括弧を使うのがケシカラン」という話はあるのですが、とりあえず記号のオーバーロード（多重定義、曖昧な使用）をしておきます。

*2:CLOSの意味の総称関数ではありません。単に型パラメータを持つ関数の意味です。

*3:混乱する状況は、プログラミング課題16に示唆されています。

*4:このようなIは終対象と呼びます。