相対モナドのクライスリ圏は簡単に作れます。が、アイレンベルク/ムーア圏はそれほど簡単ではありません。アイレンベルク/ムーア代数の定義はやや奇妙です。しかし、相対モナドの拡張スタイルの定義とは相性が良い定義になっています。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mbf}[1]{\mathbf{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
%\newcommand{\msc}[1]{\mathscr{#1}}
%\newcommand{\msf}[1]{\mathsf{#1}}
\newcommand{\mbb}[1]{\mathbb{#1}}
\newcommand{\In}{\text{ in }}
%\newcommand{\twoto}{\Rightarrow }
%\newcommand{\op}{\mathrm{op} }
%\newcommand{\id}{\mathrm{id}}
%\newcommand{\u}[1]{\underline{#1}}
%\newcommand{\o}[1]{\overline{#1}}
\newcommand{\hyp}{ \text{-} }
%\newcommand{\Iff}{ \Leftrightarrow }
%\newcommand{\Imp}{ \Rightarrow }
\newcommand{\FinSet}{\mathbf{FinSet}}
\newcommand{\Set}{\mathbf{Set}}
`$
内容:
相対モナド
相対モナドの定義は次の過去記事にあります。
他に以下の過去記事達でも相対モナドを話題にしています。
相対モナドは、モノイド・スタイルではなくて拡張スタイルで定義します。拡張スタイルのモナドの定義は以下の記事にあります。
さて、$`J:\cat{C}\to \cat{D}`$ をルート関手として固定します。ルート関手 $`J`$ 上の相対モナド $`T`$ を、記号の乱用で次のように書きます。
$`\quad T = (T, \eta, (\hyp)^\#)/J`$
相対モナド $`T`$ のクライスリ射とは、次の形をした射です。
$`\text{For }X, Y\in |\cat{C}|\\
\quad f : J(X) \to T(Y)\In \cat{D}
`$
クライスリ射を射とする圏、つまりクライスリ圏は容易に定義できます。相対モナド $`T`$ のクライスリ圏を $`\mrm{Kl}(T)`$ と書きます。
通常のモナドの場合、クライスリ圏と共にアイレンベルク/ムーア圏も定義します。相対モナド $`T`$ に対してもアイレンベルク/ムーア圏 $`\mrm{EM}(T)`$ を定義しましょう。
アイレンベルク/ムーア代数
通常のモナドの場合、アイレンベルク/ムーア代数は、$`(A, a)`$ というペアです。ここで:
- $`A`$ は、ルート圏〈基礎圏〉 $`\cat{C}`$ の対象
- $`a`$ は、ルート圏内の射 $`a:T(A)\to A\In \cat{C}`$
- 結合法則と単位法則を満たす。
結合法則の記述には $`T(T(A))`$ が必要になりますが、相対モナドでは $`TT`$ の定義ができません。アイレンベルク/ムーア代数の定義に演算 $`a:T(A)\to A`$ を使うわけにはいきません。
演算の代わりに、クライスリ拡張と似た拡張を使うことにします。拡張スタイルのアイレンベルク/ムーア代数は、$`(A, \alpha)`$ というペアです。$`A`$ は($`\cat{C}`$ ではなくて) $`\cat{D}`$ の対象です。$`A`$ を、アイレンベルク/ムーア代数の台対象〈underlying object | carrier〉と呼びます。$`\alpha`$ は拡張(後述)なので、アイレンベルク/ムーア拡張〈Eilenberg-Moore extension〉と呼びましょう。
アイレンベルク/ムーア拡張は、次の形の射に作用します。
$`\text{For }X\in |\cat{C}|\\
\quad v: J(X) \to A \In \cat{D}
`$
拡張の結果は次のようになります。
$`\quad \alpha(v) : T(X)\to A \In \cat{D}`$
アイレンベルク/ムーア拡張の正確な仕様を、依存型理論のパイ型を使って書けば次のようです。
$`\quad \alpha \in \prod_{X\in |\cat{C}|}\mrm{Map}(\cat{D}(J(X), A),\, \cat{D}(T(X), A) )`$
$`\alpha`$ は、拡張対象である射 $`v`$ の域を $`J(X)`$ から $`T(X)`$ に拡張します。域を拡張することはクライスリ拡張と同じです。
アイレンベルク/ムーア拡張の法則
アイレンベルク/ムーア拡張も、結合法則と単位法則に相当する法則〈公理〉を満たす必要があります。「絵算で見る、拡張スタイルのモナドとモノイド・スタイルのモナド // 拡張スタイルのモナドの定義」において、「入れ子律、外単位律、内単位律」という言葉を使ったので、それに合わせて「入れ子法則、単位法則」を使います(「律」と「法則」は同義です)。アイレンベルク/ムーア拡張では単位法則はひとつ(外側の単位法則)しかありません。
拡張ボックスは計算に便利なので、拡張ボックスを使った絵算〈{graphical | pictorial | diagrammatic} {calculation | computantion}〉により入れ子法則と単位法則を記述します。
描画法に関して次の約束をします。
- $`\cat{C}, \cat{D}`$ の対象は実線のワイヤーで描く。
- $`J`$ は点線のワイヤーで描く。
- $`T`$ は実線に1本以上の斜線を添えたワイヤーで描く。
- $`\cat{D}`$ の射は丸いノードで描く。
- 拡張はボックスで描く。
- クライスリ拡張のボックスには $`\#`$ を、アイレンベルク/ムーア拡張のボックスには $`\alpha`$ を添える。
- テキストで書くときも、アイレンベルク/ムーア拡張を $`\alpha(v)`$ ではなくて $`v^\alpha`$ と書く。
基本的なことは「絵算で見る、拡張スタイルのモナドとモノイド・スタイルのモナド」をみてください。
入れ子法則〈nest law〉は以下の絵のようになります。
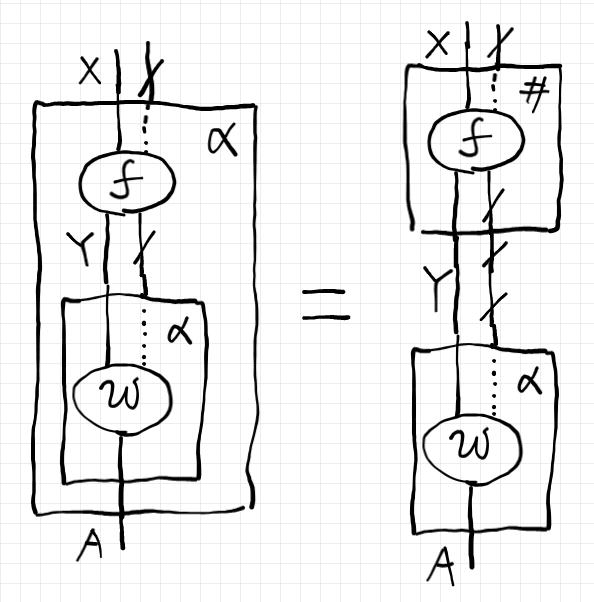
アイレンベルク/ムーア拡張を入れ子に繰り返したものは、クライスリ拡張とアイレンベルク/ムーア拡張の結合に平坦化できます。テキスト等式で書けば次のようです。
$`\text{For }X, Y\in |\cat{C}|\\
\text{For }w : J(Y)\to A \In \cat{D}\\
\text{For }f : J(X)\to T(Y) \In \cat{D}\\
\quad (f ; w^\alpha)^\alpha = f^\# ; w^\alpha \; : T(Y)\to A
\In \cat{D}
`$
単位法則〈unit law〉は以下の絵のようになります。
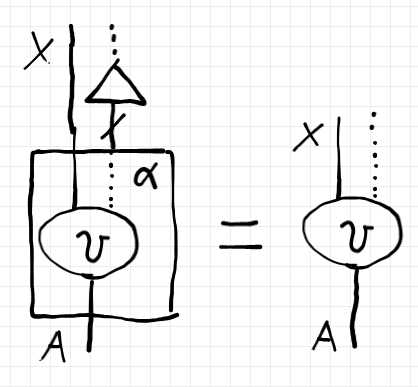
拡張ボックスの外に単位をプレ結合すると、単位と共にボックスが消えます。テキスト等式で書けば次のようです。
$`\text{For }X\in |\cat{C}|\\
\text{For }v : J(X)\to A \In \cat{D}\\
\quad \eta_X ; v^\alpha = v \; : J(X) \to A \In \cat{D}
`$
$`(A, \alpha)`$ と $`(B, \beta)`$ が $`T`$ のアイレンベルク/ムーア代数のとき、台集合のあいだの射 $`f: A \to B\In \cat{D}`$ がアイレンベルク/ムーア拡張を保存するとき(下図)、$`f`$ はアイレンベルク/ムーア代数のあいだの準同型射〈homomorphism〉だとします。
$`\text{For }X\in |\cat{C}|\\
\text{For }v: J(X) \to A\In \cat{D}\\
\xymatrix{
T(X) \ar@{=}[r] \ar[d]_{v^\alpha}
&{T(X)} \ar[d]^{(v; f)^\beta}
\\
A \ar[r]_f
&B
}\\
\quad \text{commutative }\In \cat{D}
`$
以上の定義により、相対モナド $`T`$ のアイレンベルク/ムーア圏 $`\mrm{EM}(T)`$ が定義されます。
実例: ベクトル空間
$`\FinSet`$ を有限集合達と写像達の圏、$`\Set`$ を集合達と写像達の圏とします。$`\mrm{J}`$ は、有限集合を集合とみなす埋め込み関手とします。
$`\quad \mrm{J}: \FinSet \to \Set \In \mbf{CAT}`$
$`\mrm{J}`$ をルート関手とします。
$`K`$ を適当な無限体として*1、線形結合相対モナド $`\mrm{L}_K`$ を考えます。
$`\quad \mrm{L}_K = (\mrm{L}_K, \eta, (\hyp)^\#)`$
有限集合 $`X \in |\FinSet|`$ に対して、$`\mrm{L}_K(X)`$ は、$`X`$ の要素達の$`K`$-係数線形結合〈一次結合〉達の集合です。$`X`$ が有限集合でも、$`\mrm{L}_K(X)`$ が有限とは限りません($`X = \emptyset`$ 以外では無限集合)。
- 相対モナドの単位 $`\eta_X`$ は、$`X`$ の要素を単一項の線形結合だとみなすこと。
- 相対モナドのクライスリ拡張 $`f\mapsto f^\#`$ は、$`f: X \to \mrm{L}_K(Y)`$ を線形に拡張する操作。
これらは相対モナドを形成します。
相対モナド $`\mrm{L}_K`$ のアイレンベルクムーア代数はベクトル空間です。ベクトル空間の台集合を $`A`$ とします。ベクトル空間としての構造は、$`A`$ 上の演算(足し算とスカラー倍)として定義されるのではなくて、$`A`$ への写像を拡張する能力として定義されます。つまり、台集合 $`A`$ とアイレンベルク/ムーア拡張 $`\alpha`$ のペア $`(A, \alpha)`$ がベクトル空間です。
$`\text{For }X \in |\FinSet|\\
\text{For }v : \mrm{J}(X) \to A \In \Set\\
\quad v^\alpha : \mrm{L}_K(X) \to A \In \Set
`$
アイレンベルク/ムーア拡張 $`\alpha`$ は、あらゆる有限集合 $`X`$ と、あらゆる写像 $`v:\mrm{J}(X)\to A`$ について定義されなくてはなりません。$`\alpha`$ は大規模な仕掛けです。
通常のベクトル空間の定義では、足し算 $`A\times A \to A`$ とスカラー倍 $`A\times K \to A`$ という2つの写像だけで代数構造が定義できます。それに対して、アイレンベルク/ムーア拡張 $`\alpha`$ は無限個の写像が必要です。しかも小さな集合にならないほどの無限個です。
奇妙な感じはするのですが、「個体の性質や構造も、世界全体との関わりにおいて規定される」という圏論の精神には沿っている定義だとも言えます。
*1:有限体だと、有限集合達の圏だけで完結してしまいます。$`\mrm{J}`$ の出番がありません。