次の論文を斜め読みしました。
- [BGCLB23-]
- Title: Neural Sheaf Diffusion: A Topological Perspective on Heterophily and Oversmoothing in GNNs
- Authors: Cristian Bodnar, Francesco Di Giovanni, Benjamin Paul Chamberlain, Pietro Liò, Michael M. Bronstein
- Submitted: 9 Feb 2022 (v1), 6 Jan 2023 (v4)
- Pages: 29p
- URL: https://arxiv.org/abs/2202.04579
この論文のなかに「セルラー層」とか「層ラプラシアン」とかの言葉が出てきます。「これを『層〈sheaf〉』と呼ぶのはどうなのよ?(やや欺瞞的)」という気もします。まーそれはともかく、「セルラー層」「層ラプラシアン」の定義が唐突です。紙幅の都合からでしょうが、通常の「層」や「ラプラシアン」との関係が書いてありません。そこらへんを勝手に補ってみます。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mbf}[1]{\mathbf{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\twoto}{\Rightarrow}
%\newcommand{\msc}[1]{\mathscr{#1}}
%\newcommand{\msf}[1]{\mathsf{#1}}
%\newcommand{\mbb}[1]{\mathbb{#1}}
%\newcommand{\o}[1]{\overline{#1} }
\newcommand{\u}[1]{\underline{#1} }
%\newcommand{\op}{\mathrm{op} }
%\newcommand{\id}{\mathrm{id} }
\newcommand{\In}{\text{ in } }
\newcommand{\hyp}{\text{-} }
\newcommand{\bs}[1]{\boldsymbol{#1}}
%\newcommand{\Imp}{\Rightarrow }
`$
内容:
- 前提と注意事項
- グラフ・ラプラシアン
- 関数の古典的な表示による解釈
- グラフの近傍バンドル
- グラフ・ラプラシアンの導出
- 調和関数と平均値性
- スカラー場から異種混合ベクトル場へ
- 異種混合ベクトル場
- 上昇写像と下降写像
- 異種混合ベクトル場に対するグラフ・ラプラシアン
- おわりに
前提と注意事項
当該論文 [BGCLB23-] 内で「グラフ」という用語の明示的な定義はないのですが、どうやら単純無向有限グラフを単に「グラフ〈graph〉」と呼んでいるようです。多重辺はもちろん、自己ループ辺も許しません。無向辺は、異なる二頂点のあいだに一本だけ許されるということです。
グラフの頂点に何らかの量が割り当てられているとき、その量を(頂点の)特性〈feature〉と呼びます。「グラフの頂点」と「特性」を物理の言葉で言えば、「空間の点」と「場」になります。スカラー場〈関数〉はスカラー特性〈scalar feature〉、ベクトル場はベクトル特性〈vector feature〉に対応します。
[BGCLB23-] では、グラフに伴う“とある構造”をセルラー層〈cellular sheaf〉と呼んでいます。層の離散化だと言えなくもないですが、多様体上の層などとハッキリした対応があるわけではないです。「茎〈stalk〉」、「制限写像〈restriction map〉」などの層の用語を流用してますが、これらも雰囲気的に使っていると思ったほうがいいでしょう。
空間を離散化すると、層とベクトルバンドルの区別はハッキリしなくなります。なので、セルラー層は、ベクトルバンドルの離散化だとも言えます。実際、制限写像がd-次元の直交行列であるセルラー層を離散 $`O(d)`$ バンドル〈discrete $`O(d)`$ bundle〉と呼んでいます。セルラー層をバンドルと解釈するときは、制限写像は接続〈connection〉とみなしています。
以下は、[BGCLB23-] の図2のコピーです。図の説明文からも、離散ベクトルバンドル〈discrete vector bundle〉とセルラー層〈cellular sheaf〉を同義語として使っていることが分かります。
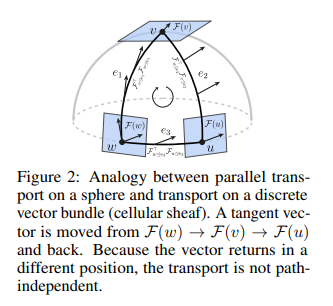
ところで、バンドルとグラフが両方出てくる文脈だと、「接続」という日本語が connection と incidence でコンフリクト〈衝突〉してしまいます。グラフの“頂点と辺の incidence”はカタカナ書きで「インシデンス」とします。グラフの incidence matrix は「インシデンス行列」です(通常は「接続行列」)。
バンドルの接続(っぽい構造)を定義する写像は接続写像〈connection map〉、その行列表示なら接続行列〈connection matrix〉、あるいは単に接続〈connection〉と呼びます。
この記事内で、以下は同義語です。
- セルラー層 = 離散ベクトルバンドル
- セルラー層の茎 = 離散ベクトルバンドルのファイバー
- セルラー層の制限写像 = 離散ベクトルバンドルの接続写像
グラフ・ラプラシアン
$`G`$ をグラフ〈単純無向有限グラフ〉とします。$`G`$ に関連する集合や行列を次のように定義します。
- $`V_G`$ : $`G`$ の頂点達の集合
- $`E_G`$ : $`G`$ の辺〈無向辺〉達の集合
- $`A_G`$ : $`G`$ の隣接行列〈adjacent matrix〉
- $`M_G`$ : $`G`$ のインシデンス行列(この記事内では使わない)
- $`D_G`$ : $`G`$ の次数行列〈degree matrix〉(後述)
- $`L_G`$ : $`G`$ のラプラシアン行列〈Laplacian matrix〉(後述)
文脈から $`G`$ が了解されているなら、下付きの $`G`$ は省略します。
隣接行列 $`A`$ は、 $`V\times V`$ をインデックスの集合とする$`\{0, 1\}`$-係数の行列です。インシデンス行列 $`M`$ は、$`V\times E`$ をインデックスの集合とする$`\{0, 1\}`$-係数の行列です。次数行列は、$`V\times V`$ をインデックスの集合とする$`\mbf{N}`$-係数の行列です。対角成分に頂点の次数が入り、非対角成分はゼロです。ラプラシアン行列は $`L := D - A`$ と定義されます -- これは唐突でしょうから後でさらに説明します。
以下は、"Survey of Graph Neural Networks and Applications" からのコピーで、グラフの次数行列、隣接行列、ラプラシアン行列の例です。
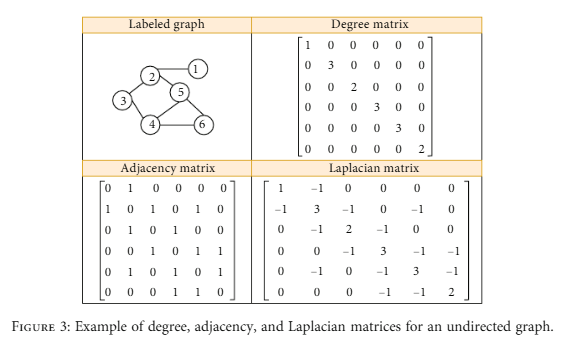
グラフのラプラシアン行列は、グラフ・ラプラシアン〈graph Laplacian〉、あるいは単にラプラシアン〈Laplacian〉とも呼びます。これは、連続の場合のラプラシアンの離散版と位置付けられます。
n次元ユークリッド空間上の連続版のラプラシアンは、次のような二階微分作用素です*1。
$`\quad \Delta = \nabla^2 := \sum_{i = 1}^n \frac{\partial^2}{ {\partial x_i}^2}`$
例えば2次元ユークリッド空間上ならば:
$`\quad \Delta = \frac{\partial^2}{ {\partial x}^2} + \frac{\partial^2}{ {\partial y}^2}
= \frac{\partial}{ {\partial x}}\frac{\partial}{ {\partial x}} + \frac{\partial}{ {\partial y}}\frac{\partial}{ {\partial y}}
`$
n次元ユークリッド空間内の領域 $`S\subseteq \mbf{R}^n`$ 上にスカラー場があり、それが時間的に変化するとします。時間区間を $`I`$ ($`I\subseteq \mbf{R}`$)とすると、変化する(かも知れない)スカラー場は以下のような関数(十分なめらかとする)として表せます。
$`\quad \phi : S\times I \to \mbf{R}`$
次の偏微分方程式が拡散方程式〈diffusion equation〉です(時間微分は $`\frac{d}{dt}`$ で書きます)。
$`\quad \frac{d\phi(\bs{x}, t)}{dt} = k \Delta \phi(\bs{x}, t)
= k \sum_{i = 1}^n \frac{\partial^2 \phi(\bs{x}, t)}{ {\partial x_i}^2}
`$
ここで、$`k`$ は実数定数(拡散定数)です。もっと複雑な形の拡散方程式もありますが、ここではこの形に限ります。
領域 $`S`$ をグラフ $`G`$ で離散有限近似した/できたとして、拡散方程式も離散化できます。時間は連続のままだとして次の形になります。
$`\quad \frac{d\phi(v, t)}{dt} = k \sum_{\{w, v\}\in E} (\phi(v, t) - \phi(w, t))`$
これは次のように読めます。
- スカラー場〈スカラー特性〉$`\phi`$ の頂点 $`v`$ における時間微分(変化率)は、$`v`$ と隣接する頂点との“値の差”の総和に比例する。
ここで、引き算 $`\phi(v, t) - \phi(w, t)`$ の順序はどうでもよくて、$`\phi(w, t) - \phi(v, t)`$ でもかまいません。符号や定数倍の違いは拡散定数 $`k`$ の取り方で調整できます。
隣接行列 $`A`$ を用いて書き換えれば次のようになります(詳細は後述)。
$`\quad \frac{d\phi(v, t)}{dt} = k \sum_{w \in \mrm{NbV}(v) }( \phi(v, t) - \phi(w, t) )\\
\qquad = k \sum_{w \in V } ( A_{w, v}(\phi(v, t) - \phi(w, t))
`$
ここで、$`\mrm{NbV}(v)`$ は、頂点 $`v`$ に隣接する頂点〈Neighborhood Vertex〉達の集合です。
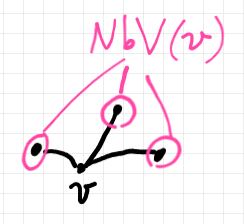
左辺の総和部分がグラフ・ラプラシアンの表示です。グラフ・ラプラシアンの表示については、後でまた具体的に詳しく計算します。
関数の古典的な表示による解釈
前節の $`\phi`$ は、グラフの頂点集合 $`V = V_G`$ 上のスカラー場〈スカラー特性〉で時間変数を持つものでした。
$`\quad \phi \in \mrm{Map}(V\times I, \mbf{R})`$
$`\phi`$ をカリー化した関数を同じ名前 $`\phi`$ で表すと:
$`\quad \phi \in \mrm{Map}(I, \mrm{Map}(V, \mbf{R}) )\\
\text{i.e.}\\
\quad \phi : I \to \mrm{Map}(V, \mbf{R})
`$
有限集合 $`V`$ に $`1, 2, \cdots, n`$ で番号を振ります。あるいは、最初から $`V =\{1,2, \cdots, n\}`$ だったとしましょう。すると:
$`\quad \mrm{Map}(V, \mbf{R}) \cong \mrm{Map}(\{1, \cdots, n\}, \mbf{R})
= \mbf{R}^{ \{ 1, \cdots, n\} } \cong \mbf{R}^n
`$
この同型により、グラフ $`G`$ 上の変化する(かも知れない)スカラー場 $`\phi`$ は、n次元ユークリッド空間への(なめらかな)一変数写像と同一視できます。
$`\quad \phi : I \to \mbf{R}^n \:\text{ where }I \subseteq\mbf{R}`$
記述としては、n次元空間における粒子の運動と同じになります。$`n \le 3`$ なら、運動の軌跡を視認可能な曲線に描けます。拡散方程式は、関数空間とみなした $`\mbf{R}^n`$ 内での運動を支配する運動法則(時間発展の法則)になります。
関数 $`\phi`$ を古典的な記法($`y = f(x)`$ 形式)で書くならば:
$`\text{For }t\in I\\
\quad x_i = \phi_i(t) \:\: ( i = 1, \cdots, n)`$
時間微分をニュートン記法(ドットを載せる)で書くと、空間離散化された拡散方程式は次のように書けます($`L`$ はグラフ・ラプラシアン)。
$`\quad \dot{\bs{x}} = \frac{d}{dt}\phi = kL \phi`$
ベクトル変数 $`\bs{x} = (x_i)_{i = 1,\cdots, n}`$ に暗黙に時間変数が含まれているとすれば、$``$ 次のように書いてもいいでしょう。
$`\quad \dot{\bs{x}} = kL \bs{x}`$
行列計算の習慣と合わせるためには、$`\bs{x}`$ は縦ベクトルの形で書きます。
$`\quad \bs{x} =
\begin{bmatrix}
x_1\\
\vdots\\
x_n
\end{bmatrix}
`$
このベクトルは、各頂点ごとのスカラー値を縦に並べたもので、スカラー特性〈スカラー場〉です。ベクトル特性〈ベクトル場〉ではありません。ベクトル特性は、各頂点ごとの値がベクトルの場合です*2。
空間離散化拡散方程式 $`\dot{\bs{x}} = kL \bs{x}`$ の言っていることは、ある時点のスカラー場(を表す縦ベクトル)$`\bs{x}`$ にラプラシアン行列 $`L`$ を掛けて $`k`$ 倍すると、その時点での時間微分(変化の速度ベクトル) $`\dot{\bs{x}}`$ が得られる、ということです。
グラフの近傍バンドル
離散化された空間であるグラフ $`G`$ には、多様体のような接バンドル〈接ベクトルバンドル〉や余接バンドル〈余接ベクトルバンドル〉の概念がありません。接バンドルに類似の無限小近傍の概念を導入します。グラフ上の無限小とは実は有限で、ある頂点に隣接している頂点達やインシデンスな〈入り込む | 流入している〉辺達のことです。
以下のような具体的な六頂点グラフ $`G`$ で説明します。$`V = V_G = \{1, \cdots, 6\}`$ です。
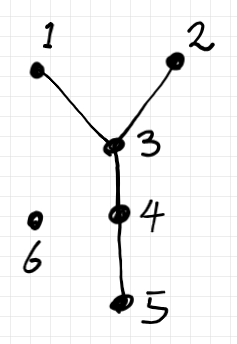
グラフの頂点 $`i\in V`$ ごとに、その近傍グラフ〈neighborhood graph〉 $`\mrm{Nb}(i) = \mrm{Nb}_G(i)`$ を以下に定義します。近傍グラフは有向グラフです。
例えば、頂点 $`3`$ に注目すると、近傍グラフ $`\mrm{Nb}(3)`$ は以下のピンク色で描かれた有向グラフです。近傍グラフは、頂点 $`3`$ に隣接する頂点達とインシデンスな(接続している)辺達からなります。ただし、辺には、$`3`$ に流入する向きを付けます。辺に向きがあるので、近傍グラフは有向グラフです。流入する向きは単なる習慣で、流出する向きだと約束しても何ら問題ありません。しかし、どっちかに決めたら一貫して同じ向きを使う必要があります。
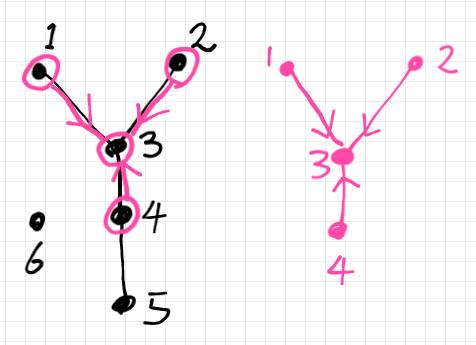
すべての頂点に渡って、近傍グラフを列挙すると以下のようです。ここで描かれている円周は、レイアウトの目安で近傍グラフの一部ではありません。
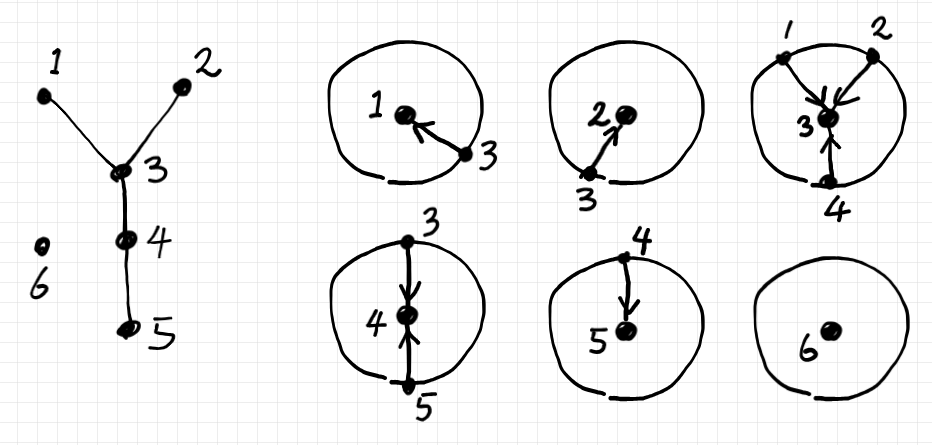
各頂点の場所からその近傍グラフを“生やすと”、近傍グラフをファイバーとするバンドルができます。絵に描くと次のような感じです。
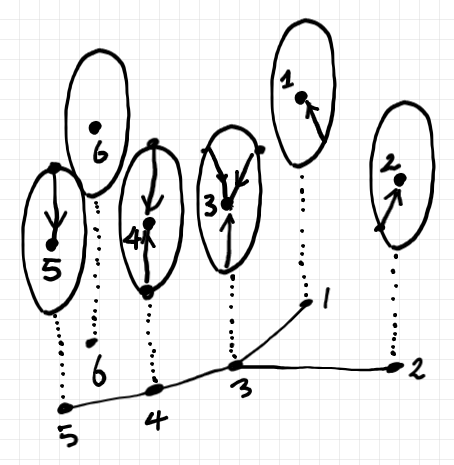
このバンドルの全空間〈total space〉は有向グラフです。円周を取り除いて、レイアウトも少し変えて描けば以下のようです。
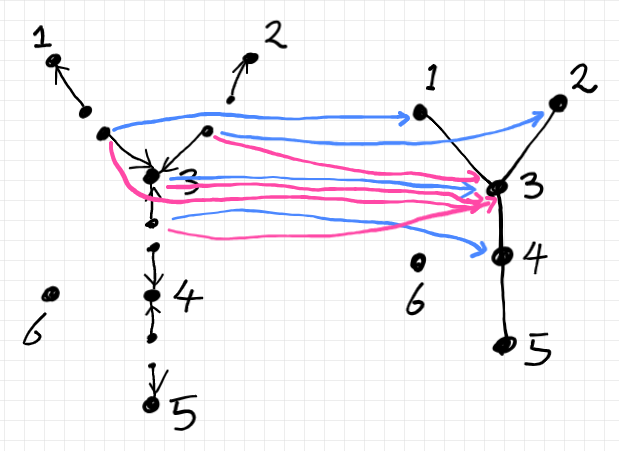
ここで、水色の矢印は、ファイバー $`\mrm{Nb}_G(3)`$ の頂点・有向辺が底空間(もとのグラフ)とどう対応するかを示しています。水色はバンドルの射影ではありません。ピンク色の矢印がバンドルの射影で、ファイバー内のすべての頂点が一点に“落ち”ます。
「ファイバー内の有向辺の、射影による行き先が無い」とか、「異なる頂点の上のファイバー間の関係性(接続)が無い」とか、幾何的ファイバーバンドルとしては不具合がありますが、当面の目的には問題ありません。
上記のバンドル構造を、$`G`$ の近傍グラフバンドル〈neighborhood-graph bundle〉、あるいは短く近傍バンドル〈neighborhood bundle〉と呼ぶことにします。近傍グラフバンドルの全空間は $`\mrm{NB}(G)`$ (B が大文字)と書きます。ファイバーは $`\mrm{NB}_i(G)`$ です。したがって:
$`\quad \mrm{NB}_i(G) = \mrm{Nb}_G(i) = \mrm{Nb}(i)`$
ウーム、記法が混乱誘発的〈confusing〉ですね。カンベンしてね*3。
有向グラフ $`\mrm{Nb}(i)`$ の頂点集合は、近傍頂点達の集合 $`\mrm{NbV}(i)`$ と同じです。
底空間の無向グラフ(もとのグラフ)が $`n`$ 個の頂点と $`m`$ 本の無向辺を持つとき、全空間である有向グラフは $`(n + 2m)`$ 個の頂点と $`2m`$ 本の有向辺を持ちます。
頂点 $`i`$ 上のファイバーである近傍グラフ $`\mrm{NB}_i(G) = \mrm{Nb}_G(i)`$ の有向辺の集合から自由生成したベクトル空間は、点 $`i`$ での接ベクトル空間の対応物になります。ただし、頂点ごとに接ベクトル空間の次元は違うかも知れません。今扱っている具体例の六頂点グラフでは、接ベクトル空間の次元は $`0, 1, 2, 3`$ と頂点ごとにバラバラです。接ベクトル空間の次元は、頂点の次数に一致します。
グラフ・ラプラシアンの導出
連続版ラプラシアンは微分作用素なので、ラプラシアンを作用させた結果は関数〈スカラー場〉の局所的な情報で決定されます。(点ごとの)局所的な情報を離散化したものが、前節の近傍バンドルです。頂点上のファイバー(近傍グラフ)として、局所的な情報がエンコードされています。したがって、ラプラシアンの離散化は、各頂点ごとの近傍グラフにおいて計算されます。
グラフ・ラプラシアンがやることは、近傍グラフの中心点(注目している頂点)の関数〈スカラー場〉値と、近傍頂点における関数値との差をとって新しい関数値を作ることです。前節の六頂点グラフの頂点 $`3`$ における計算を具体例にしましょう。
頂点集合 $`V = V_G`$ 上で定義された関数〈スカラー場〉$`\bs{x}`$ は、以下のような縦ベクトルと同一視できます。
$`\quad \bs{x}=
\begin{bmatrix}
x_1\\
x_2\\
x_3\\
x_4\\
x_5\\
x_6\\
\end{bmatrix}
`$
頂点 $`3`$ における“近傍頂点における関数値との差”を書き下しましょう。
$`\quad k(\,(x_3 - x_1) + (x_3 - x_2) + (x_3 - x_4)\,)
= k(\, 3x_3 - (x_1 + x_2 + x_4)\,)
`$
$`\bs{x}`$ には暗黙に時間変数が含まれるとして、上記の値が変化率(関数空間内の運動速度)の第 $`3`$ 成分を与えます。
$`\quad \dot{x}_3 = k(\,(x_3 - x_1) + (x_3 - x_2) + (x_3 - x_4)\,)`$
これは離散化拡散方程式の成分です。一般的には次のように書けます。
$`\quad \dot{x}_i = k \sum_{j\in \mrm{NbV}(i)} (x_i - x_j)\\
\text{where } i = 1, \cdots, n
`$
さて、$`V`$ 上の関数〈スカラー場〉$`\bs{y}`$ に対して、次の公式が成立します。
$`\quad \sum_{j\in \mrm{NbV}(i)} y_j = \sum_{j\in V} A_{j,i}y_j`$
$`A_{j, i}`$ はグラフの隣接行列です。$`j,i`$ が辺で繋がってなければ $`A_{j, i} = 0`$ であることを考えれば等式の成立は納得できるでしょう。
上記の公式を使って次の計算ができます。
$`\quad \sum_{j\in \mrm{NbV}(i)} (x_i - x_j)\\
= \sum_{j\in V} A_{j, i}(x_i - x_j) \\
= (\sum_{j\in V} A_{j, i}x_i ) + (\sum_{j\in V} A_{j, i}x_j )
`$
ここで、$`\sum_{j\in V} A_{j, i}x_i`$ に注目して割り込みの計算をします。
$`\quad \sum_{j\in V} A_{j, i}x_i\\
= (\sum_{j\in V} A_{j, i}) x_i\\
= (D_{i, i}) x_i\\
= \sum_{j\in V} D_{j, i}x_j
`$
次のような事実を使っています。
- 隣接行列の列方向(行方向でも)の総和 $`\sum_{j\in V} A_{j, i}`$ は頂点 $`i`$ の次数 $`D_{i, i} = \mrm{deg}(i)`$ に等しい。
- 次数行列 $`D`$ は対角成分以外はゼロなので、値 $`D_{i,i}x_i`$ は、次数行列 $`D`$ と縦ベクトル $`\bs{x}`$ の第 $`i`$ 成分である $`(D\bs{x})_i`$ と同じ。
- $`(D\bs{x})_i`$ は、$`\sum_{j\in V} D_{j, i}x_j`$ として計算できる。ここで、総和を取るインデックス $`j`$ の名前は何でもいい(束縛変数は任意にリネーム可能)。
割り込みの計算結果を使って、もとの計算を続ければ:
$`\quad (\sum_{j\in V} A_{j, i}x_i ) + (\sum_{j\in V} A_{j, i}x_j )\\
= (\sum_{j\in V} D_{j, i}x_j) + (\sum_{j\in V} A_{j, i}x_j )\\
= \sum_{j\in V}(D_{j, i} - A_{j, i})x_j \\
= ( (D - A)\bs{x})_i
`$
したがって、拡散方程式は次のように書けます。
$`\quad \dot{x}_i = k ( (D - A)\bs{x})_i \\
\text{where } i = 1, \cdots, n
`$
インデックス $`i`$ を省いて書けば:
$`\quad \dot{\bs{x}} = k (D - A)\bs{x}`$
以上で、グラフ・ラプラシアンの定義 $`L = D - A`$ が、離散化拡散方程式の現象的セマンティクスから導かれることが分かりました。
調和関数と平均値性
グラフ $`G`$ の頂点集合 $`V = V_G`$ 上で定義された関数〈スカラー場 | スカラー特性〉が、グラフ・ラプラシアンを作用させてゼロになるとき、調和関数〈harmonic function〉といいます。関数空間 $`\mrm{Map}(V, \mbf{R})`$ を $`\mbf{R}^n`$ と同一視して、グラフ・ラプラシアン $`L = L_G`$ を$`n`$次正方行列、まるいは正方行列で表示される線形写像と同一視するなら:
$`\quad \bs{x} \in \mbf{R}^n \text{ is harmonic}
\iff \bs{x} \in \mrm{Ker}(L)
`$
$`\bs{x}`$ が調和関数〈調和スカラー場 | 調和スカラー特性〉であることを、成分表示で書くなら:
$`\forall i\in V.\\
\quad \sum_{j\in \mrm{NbV}(i) }(x_i - x_j ) = 0
`$
次数行列 $`D = D_G`$ と隣接行列 $`A = A_G`$ を使って書けば:
$`\forall i\in V.\\
\quad D_{i,i} x_i - \sum_{j\in V } A_{j, i}x_j = 0
`$
先の六頂点グラフの具体例において、$`i = 3`$ の場合ならば:
$`\quad 3 x_3 - (x_1 + x_2 + x_4) = 0`$
等式を変形すると:
$`\forall i\in V.\\
\quad x_i = \frac{1}{D_{i,i}} \sum_{j\in V } A_{j, i}x_j
`$
$`D_{i,i}`$ は頂点 $`i`$ の次数 $`\mrm{deg}(i)`$ であり、隣接行列による掛け算は、頂点 $`i`$ の近傍頂点集合における総和だから、次のようになります。
$`\forall i\in V.\\
\quad x_i = \frac{1}{\mrm{deg}(i)} \sum_{j\in \mrm{NbV}(i) } x_j
`$
ここまで書き換えれば、調和関数が「どのような関数か?」がハッキリします。調和関数とは:
- 頂点 $`i`$ での値 $`x_i`$ が、近傍頂点達の集合 $`\mrm{NbV}(i)`$ 上での $`x_j`$ 達の平均値に等しい関数。
六頂点グラフの $`i = 3`$ の場合ならば:
$`\quad x_3 = \frac{1}{3}(x_1 + x_2 + x_4)`$
調和関数においては、特定の点での値(ポテンシャルとみなせる)と近傍での値の格差がない(平準化されている)ので、ポテンシャル差(典型例:電位差)が引き起こす変動(典型例:電流)が生じません。
拡散方程式は $`\dot{\bs{x}} = k L\bs{x}`$ の形だったので、ラプラシアンによる値 $`L\bs{x}`$ が、運動(時間発展)の駆動力になっているのでした。$`\bs{x}`$ が調和関数だと、運動(変化・変動)が駆動されないので、ラプラシアンによる拡散現象の安定状態/平衡状態〈equilibrium〉/不動点になります。
スカラー場から異種混合ベクトル場へ
今までの話は、グラフ上のスカラー場〈スカラー特性〉に働くグラフ・ラプラシアンの話でした。冒頭で紹介した論文 [BGCLB23-] の眼目は、スカラー場をベクトル場に拡張することです。それも、単一のベクトル空間に値をとる関数ではなくて、頂点ごとに異なるかも知れないベクトル空間に値をとるベクトル場です。このようなベクトル場を異種混合ベクトル場〈heterophilic vector field〉と呼ぶことにします。heterophilic は [BGCLB23-] で使われている言葉です。
ここから先、グラフ上の異種混合ベクトル場〈異種混合ベクトル特性〉と、それに働くラプラシアンを導入します。しかし、 [BGCLB23-] とは僅かに違った方法を採用します。連続の場合(多様体上の微分幾何など)との連絡がスムーズになるように、ベクトル値1次微分形式を意識したスタイルにします。
この節では、(離散化された)異種混合ベクトル場を記述するための準備をします。
グラフ $`G`$ は単純無向グラフなので、頂点 $`i, j`$ を結ぶ無向辺は二元集合 $`\{i, j\} = \{j, i\}`$ の形に書けます。自己ループ辺を認めてないので、単元集合 $`\{i, i\} = \{i\}`$ は現れません。無向辺 $`\{i,j\}`$ に向きを付けると二本の有向辺が得られます。それらの有向辺を $`\vec{ij},\, \vec{ji}`$ とします。こうして作った $`G`$ の有向辺達の集合を $`\vec{E} = \vec{E}_G`$ と書くことにします。
$`\vec{E}`$ は「無向グラフの有向辺達の集合」です。言い回しは奇妙ですが意味は明確なので、言い回しに惑わされないでください。$`\vec{E}`$ は有限集合で、$`E`$ の2倍の基数(要素の個数)を持ちます。$`\vec{E}`$ 上に $`\vec{ij}\sim \vec{ji}`$ という同値関係 $`\sim`$ を入れると:
$`\quad E \cong \vec{E}/\sim`$
$`\mrm{src}(\vec{ij})= i, \mrm{trg}(\vec{ij})=j`$ と定義すれば、$`(V, \vec{E}, \mrm{src}, \mrm{trg})`$ は有向グラフになります。この有向グラフは $`2m`$ 本の有向辺を持ちます($`m`$ は無向辺の本数)。有向グラフ $`(V, \vec{E},\mrm{src},\mrm{trg})`$ を $`\vec{G}`$ と略記します。有向グラフ $`\vec{G}`$ は、$`G`$ の近傍バンドル(の全空間)$`\mrm{NB}(G)`$ と同型ではありませんが、次は成立します。
$`\quad \vec{E} = \mrm{Edge}(\mrm{NB}(G))`$
次のような、有向グラフのあいだの準同型射があります。
$`\quad \mrm{NB}(G) \to \vec{G} \In \mbf{DiGraph}`$
この準同型射は頂点集合上で全射(2対1対応)で、辺集合上では同型(1対1対応)です -- 先に挙げた絵で“水色の矢印”で一部描いた写像とほぼ同じものです。
異種混合ベクトル場
異種混合ベクトル場とそのグラフ・ラプラシアンを定義するには、グラフ $`G`$ の頂点と辺に実数係数有限次ベクトル空間が割り当てられている必要があります。$`\mbf{FdVect}`$ を実数係数有限次元ベクトル空間達の圏だとして、この割り当ては次のようになります。
$`\quad F_\mrm{vert} : V \to |\mbf{FdVect}| \In \mbf{SET}\\
\quad F_\mrm{edge} : E \to |\mbf{FdVect}| \In \mbf{SET}\\
\quad F_\mrm{diEdge} : \vec{E} \to |\mbf{FdVect}| \In \mbf{SET}
`$
ただし、次の等式が成立しています。
$`\quad F_\mrm{diEdge}(\vec{ij}) = F_\mrm{diEdge}(\vec{ji}) = F_\mrm{edge}(\{i, j\})
`$
下付きの $`\mrm{vert}, \mrm{edge}, \mrm{diEdge}`$ は、文脈から明らかなら省略します。この記事内では省略(オーバーロード)を使ってませんが。
$`F_\mrm{vert}, F_\mrm{edge}, F_\mrm{diEdge}`$ は、いずれもベクトル空間のインデックス付きファミリー〈idexed family of vector spaces〉です。ベクトル空間ファミリーに対して、そのセクションの集合を定義します。シグマ型、パイ型、グロタンディーク構成などを引き合いに出さず、直接的定義をします。
$`\bigcup_{i\in V}\u{F_\mrm{vert}(i)}`$ は、ベクトル空間の台集合(下線で示している)達をすべて合併した集合です。ベクトル空間ファミリー $`F_\mrm{vert}`$ のセクション〈section〉とは次のような写像です。
$`\quad \bs{x} : V \to \bigcup_{i\in V}\u{F_\mrm{vert}(i)} \In \mbf{Set}\\
\text{where } x_i = \bs{x}(i) \in \u{F_\mrm{vert}(i)}
`$
$`F_\mrm{vert}`$ のセクションが異種混合ベクトル場〈heterophilic vector field〉です。$`F_\mrm{vert}`$ のすべてのセクション達の集合を $`\mrm{Sect}(F_\mrm{vert})`$ と書きます。
集合 $`\mrm{Sect}(F_\mrm{vert})`$ には、自然にベクトル空間の構造が入ります。ベクトル空間としての $`\mrm{Sect}(F_\mrm{vert})`$ も同じく(オーバーロードして)$`\mrm{Sect}(F_\mrm{vert})`$ と書きます。ベクトル空間として次の同型が成立します。
$`\quad \mrm{Sect}(F_\mrm{vert}) \cong \bigoplus_{i\in V}F_\mrm{vert}(i)
\In \mbf{FdVect}
`$
$`F_\mrm{edge}, F_\mrm{diEdge}`$ についても同様なことが言えて:
$`\quad \mrm{Sect}(F_\mrm{edge}) \cong \bigoplus_{\{i, j\}\in E}F_\mrm{edge}(\{i, j\})
\In \mbf{FdVect}\\
\quad \mrm{Sect}(F_\mrm{diEdge}) \cong \bigoplus_{\vec{ij}\in \vec{E}}F_\mrm{diEdge}(\vec{ij})
\In \mbf{FdVect}
`$
$`\mrm{Sect}(F_\mrm{edge})`$ と $`\mrm{Sect}(F_\mrm{diEdge})`$ はベクトル空間として同型にはなりません。が、$`F_\mrm{diEdge}`$ の交代的セクションだけを考えると $`\mrm{Sect}(F_\mrm{edge})`$ と同型になります。$`F_\mrm{diEdge}`$ の交代{的}?セクション〈alternating section〉とは次を満たすセクションです。
$`\text{For }\vec{ij}\in \vec{E}\\
\quad \bs{x}(\vec{ij}) = - \bs{x}(\vec{ji})
`$
$`F_\mrm{diEdge}`$ の交代的セクション達からなるベクトル空間を $`\mrm{AltSect}(F_\mrm{diEdge})`$ とします。$`\mrm{AltSect}(F_\mrm{diEdge})`$ は、ベクトル値一次微分形式の離散化として使えます。
同型 $`\mrm{Sect}(F_\mrm{edge}) \cong \mrm{AltSect}(F_\mrm{diEdge})`$ は規準的〈canonical〉ではありません。恣意的な決定により一対一対応が成立します。恣意的な決定は、無向辺ごとにその向きをひとつだけ選ぶことです。つまり、無向グラフに便宜的・一時的な向きを与えることです。
この節で導入した各種セクション空間を、多様体上のベクトルバンドルとそのセクション空間に似せた流儀で定義することが出来るし、そのほうが望ましいです。が、今ここでは手っ取り早い流儀でよしとします。
上昇写像と下降写像
スカラー場のラプラシアンを定義するとき、隣接する頂点 $`i, j`$ における値の差 $`x_i- x_j`$ を使いました。異なる頂点での値でも引き算できたわけです。しかし、異種混合ベクトル場では、異なる頂点でのベクトル値を計算することは一般的には出来ません。頂点 $`i`$ でのベクトル値 $`x_i`$ と、頂点 $`j`$ でのベクトル値 $`x_j`$ を計算可能とするには、次のような方法があります。
- $`x_i\in F_\mrm{vert}(i)`$ を $`F_\mrm{vert}(j)`$ に写像して、$`x_j\in F_\mrm{vert}(j)`$ と計算する。
- $`x_j\in F_\mrm{vert}(j)`$ を $`F_\mrm{vert}(i)`$ に写像して、$`x_i\in F_\mrm{vert}(i)`$ と計算する。
- $`x_i\in F_\mrm{vert}(i)`$ と $`x_j\in F_\mrm{vert}(j)`$ を、第三のベクトル空間に写像して、第三のベクトル空間内で計算する。
論文 [BGCLB23-] では、三番目の方法を使っています。2つのベクトル空間 $`F_\mrm{vert}(i)`$ と $`F_\mrm{vert}(j)`$ から、第三のベクトル空間 $`F_\mrm{edge}(\{i, j\})`$ への線形写像を準備して、それにより“引き算 $`x_i - x_j`$ ”を可能にしています。
今説明した線形写像を次のように書きます。
$`\quad \gamma_{i, \{i, j\}} : F_\mrm{vert}(i) \to F_\mrm{edge}(\{i,j\}) \In \mbf{FdVect}\\
\quad \gamma_{j, \{i, j\}} : F_\mrm{vert}(j) \to F_\mrm{edge}(\{i,j\}) \In \mbf{FdVect}
`$
“引き算 $`x_i - x_j`$ ”は次のように定義できます。
$`\quad \gamma_{i, \{i, j\}}(x_i) - \gamma_{j, \{i, j\}}(x_j)`$
しかし、この計算結果(差)は、ベクトル空間 $`F_\mrm{edge}(\{i, j\})`$ 内のベクトルです。頂点におけるベクトル値ではありません。ラプラシアンの定義には、差を頂点におけるベクトル値に戻す必要があります。$`\gamma_{i, \{i, j\}}`$ が可逆という条件はありません。
上記の問題を解決するために、登場するベクトル空間はすべて内積空間だとします。2つの内積空間のあいだの線形写像には、逆向きの随伴線形写像があります。$`\gamma_{i, \{i, j\}}`$ の随伴線形写像 $`\gamma_{i, \{i, j\}}^\dagger = (\gamma_{i, \{i, j\}} )^\dagger`$ により、計算した差を $`F_\mrm{vert}(i)`$ に戻せます。
$`\quad \gamma_{i, \{i, j\}}^\dagger : F_\mrm{edge}(\{i, j\}) \to F_\mrm{vert}(i)
\In \mbf{FdVect}
`$
今定義した $`{\gamma_{i, \{i, j\}} }`$ を上昇写像〈rise map〉、$`\gamma_{i, \{i, j\}}^\dagger`$ を下降写像〈fall map〉と呼ぶことにします。0次のベクトル値微分形式相当の“$`F_\mrm{vert}(i)`$ の要素”を、1次のベクトル値微分形式相当の“$`F_\mrm{edge}(\{i, j\})`$ の要素”に写像するので「上昇」です。逆向きは「下降」です。
論文 [BGCLB23-] では、上昇写像を「セルラー層の制限写像」あるいは「離散ベクトルバンドルの接続」と呼んでますが、上昇写像が接続写像や接続に直接対応するわけではないので、混乱誘発的〈confusing〉だと思い呼び名を変更しました。
- 上昇写像より、下降写像のほうが(幾分かは)層の制限写像に近い。
- 上昇写像より、上昇写像と下降写像の結合〈composition〉のほうが(幾分かは)ベクトルバンドルの接続に近い。
[BGCLB23-] における「層」「制限写像」「接続」などの言葉を、あまり生真面目に捉えないほうがいい、ということです。
異種混合ベクトル場に対するグラフ・ラプラシアン
ここまでの準備があれば、異種混合ベクトル場に対するグラフ・ラプラシアンを、スカラー場の場合の定義を真似て定義できます。
$`G`$ はグラフで、$`F_\mrm{vert}, F_\mrm{edge}`$ をベクトル空間ファミリーとします。ベクトル空間ファミリーのあいだには上昇写像 $`\gamma_{i, \{i, j\}}`$ 達と下降写像 $`\gamma_{i, \{i, j\}}^\dagger`$ 達も定義されているとします。この設定のもとで、グラフ・ラプラシアン $`L = L_{G, F}`$ は次のような自己線形写像〈linear endomorphism〉です。
$`\quad L : \mrm{Sect}(F_\mrm{vert})\to \mrm{Sect}(F_\mrm{vert}) \In \mbf{FdVect}
`$
具体的な定義は次のように与えられます。$`k`$ は拡散定数です。
$`\text{For }\bs{x} \in \mrm{Sect}(F_\mrm{vert})\\
\text{For } i \in V\\
\quad (L\bs{x})_i := k \left(
\sum_{j\in \mrm{NbV}(i)}\gamma_{i, \{i, j\}}^\dagger( \gamma_{i, \{i, j\}}(x_i) - \gamma_{j, \{i, j\}}(x_j) )
\right)
`$
この定義は、「隣接するニ頂点での値の差を取る」ことが面倒であることからゴチャゴチャしてます。しかし、スカラー場の場合のグラフ・ラプラシアンの定義の素直な拡張になっています。スカラー場のグラフ・ラプラシアンについて述べた様々なことが、(適切な変更により)ほとんど通用します。
おわりに
[BGCLB23-] が採用しているグラフ上の構造は、層の直接的離散化でもないし、ベクトルバンドルの直接的離散化でもありません。異種混合ベクトル場とそれに対するグラフ・ラプラシアンを定義するための独自の構造です。
[BGCLB23-] におけるセルラー層〈cellular sheaf〉は、グラフ上のベクトル空間ファミリーと上昇写像/下降写像の組み合わせのことです。層ラプラシアン〈sheaf Laplacian〉は、異種混合ベクトル場に対するグラフ・ラプラシアンのことです。
本来の層やベクトルバンドルにもっと近い形の定式化は出来るだろうし、高次元化(2次以上の微分形式相当物など)にはそのほうが望ましいと思います。異種混合ベクトル場に関するド・ラーム複体やホッジ分解を扱うことは興味深い課題です。
参考記事:
しかし、0次元の場合(頂点への割り当て)だけを扱うならば、ベクトル空間ファミリーと上昇写像/下降写像の組み合わせはちょうど良いセッティングです。