昨日の「デカルト閉圏における絵算」にて:
この絵の根拠(合理化)とか、絵を使った計算例とかは、たぶんそのうち。
気が変わる前に Λ[(id×out);eval;in];Λ[(id×in);eval;out] = id という等式を絵算(pictorial calculation;お絵描き計算)で完全・露骨に示してみましょう。
内容:
●基本概念/基本法則の絵
まず、昨日出しておいた基本概念/基本法則の絵ですが:
なんで、こんな絵にするのか?と聞かれれば、理由はあるから一応の説明はできるけど、説明めんどくさい。「こんな絵を使うと、計算がうまくいくよ」で、カンベンしてください。
できるだけ合理的説明をしたいのだけど、絵算は使ってみないと実感湧かないし。人手の計算は肉体労働だから、必要なのは気力・体力・紙(いっぱい)・鉛筆。… 根性論が大嫌いな僕でも、計算のときは根性出すしかないなー、疲れるけど。(「絵を描いて学ぶ・プログラマのためのラムダ計算」の「2. 計算は身体的に理解しよう」も参照。)
さて、上に挙げたリンク先に描いてある基本法則で、ベータ(β)変換とイータ(η)変換はデカルト閉圏の公理だから認めるしかない、これが出発点ですね(圏論的指数の周辺:ラムダ計算、デカルト閉圏、ノイマン型コンピュータ」参照)。左タイトニングは、いくつも状況証拠があるから心情的には「間違いない」と僕は納得しちゃうけど、ちゃんと示さないとまずいでしょうから、後ほど取り上げます。
●記号法とかの注意
今回は圏の対象を小文字で表します。大文字のほうが射と混同する危険がなくていいけど、僕はどっちでも気にしません、どっちも使います、気まぐれです。それと、idxを単にxと書くことがあります(idも使いますけどね)。baのような指数(ベキ)のidとか、上付きが下付きに入れ子で入ったりして、ゴチャゴチャするからイヤなの。
射の結合(composition;合成)は、記号「;」を使い、図式順(左から右へ)。ずっと図式順を使っているので、反図式順はもうダメ、耐えられない。
デカルト閉圏は、Λ(大文字ラムダ)で記されるオペレータを備えているわけだけど、Λは、ホムセットからホムセットへの集合論的な写像です、Λ:C(x×a, b)→C(x, ba)。当然に、x, a, b ごとにΛも変わるので、ホントは Λx,a,bのように3つのインデックス(パラメータ)を付けないといけないですね。でもめんどうだからインデックスを省略するか、一番重要なaだけ付けてΛaとか書きます。雰囲気的には、Λa(f)は、x|→λa.f(x, a) の圏論的対応物。
●Λの逆写像
Cはデカルト閉圏として、ホムセットのあいだの写像Λ:C(x×a, b)→C(x, ba) (正確にはΛx,a,b)は可逆です。つまり、Γ(大文字ガンマ)という写像C(x, ba)→C(x×a, b) があって、Γ(Λ(f)) = f (f∈C(x×a, b))、Λ(Γ(h)) = h (h∈C(x, ba))。
Γの具体的な形は、Γ(h) = (h×a);eval です。Γ(Λ(f)) = f、Λ(Γ(h)) = h を示すのに、なにも絵算を持ち出す必要もないのですが、目を慣らすために絵算でやってみましょう。
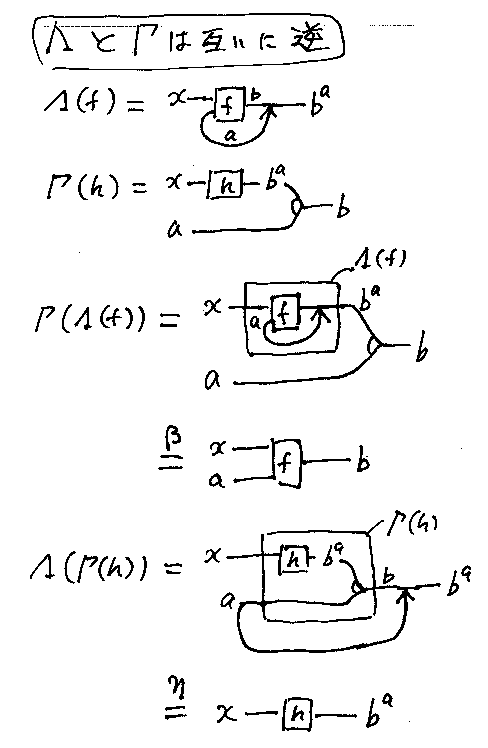
Γ(Λ(f)) = f はベータ変換、Λ(Γ(h)) = h はイータ変換に他なりません。つまり、デカルト閉圏の公理であるベータ変換とイータ変換は、Λの可逆性を主張していることになります。コレ大事、書いておきましょう(↓)。
- [1] ΛとΓは互いに逆
[追記]指数を表す矢印は逆向きがよかったかも。それで、ワイヤーとか接合部(eval)とかをうんと写実的に描くと、ベータ変換/イータ変換も恐ろしくリアリティがある(バリバリバリとかグモーグチャベタとかの音が聞こえる)操作になるんだけど、そこまで描き込む気力はない。[/追記]
●idとevalの関係
baの恒等射(id)とeval:ba×a→b は、ΓとΛで互いに移りあいます。定義より、Γ(id) = (id×a);eval 、これは自明にevalなので、Γ(id) = eval。この等式の両辺にΛを作用させれば、Λ(Γ(id)) = Λ(eval) ですが、ΛとΓは逆だったので、id = Λ(eval)。まとめれば、
- [2] Γ(id) = eval
- [3] Λ(eval) = id
念のため絵算で描けば:
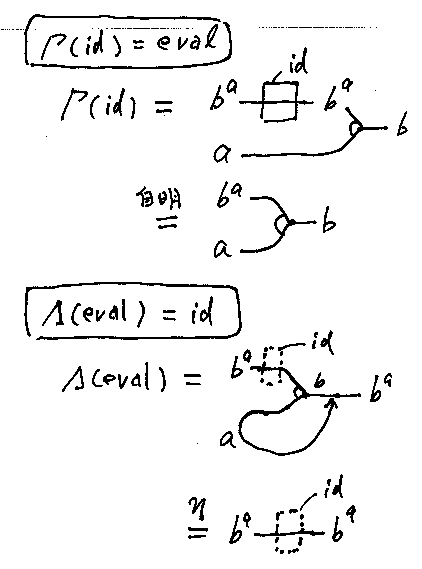
●左タイトニング公式
基本法則に、次の図で示される左タイトニング(left tightening)を入れておきました。(ちなみに、右タイトニングはありません。)
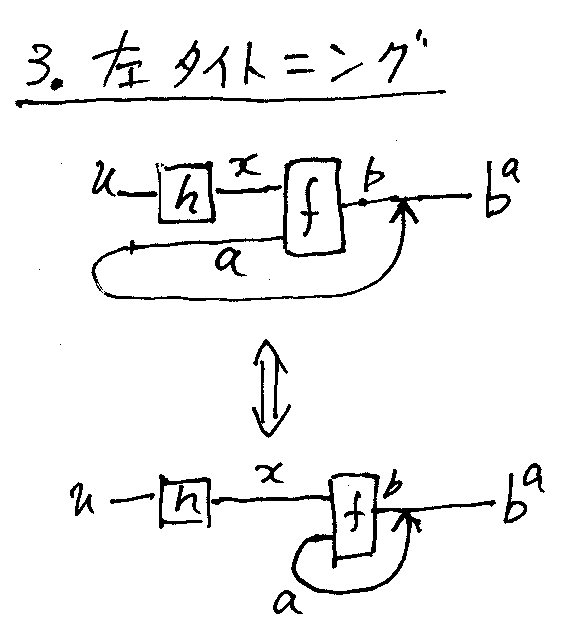
これをなぜタイトニングと呼んだかは、http://www.chimaira.org/docs/Superposing_figs.htm の図と比べてもらえればわかるでしょう。
左タイトニングを等式で書けば、
- [4] h;Λ(f) = Λ[(h×a);f]
ですが、両辺にΓを作用させて、「[1]ΛとΓは互いに逆」を使えば、
- [4'] Γ(h;Λ(f)) = (h×a);f
Γは具体的な表示があるので、それを使って計算してみると:
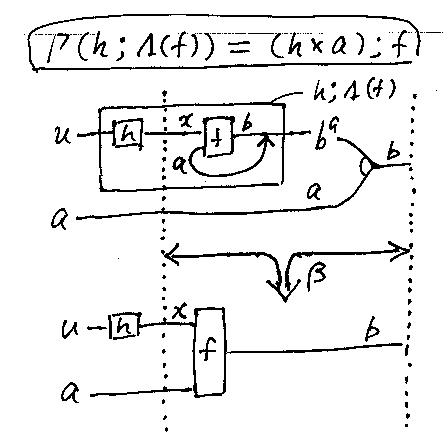
点線で挟まれた帯状の部分にベータ変換を施しただけです。[4']にΛを作用させれば[4]に戻ります。よって、左タイトニング公式はデカルト閉圏で成立します。
●Λ(g) = id ⇔ g = eval
さほど深い意味はありませんが、計算を少し簡単にする目的で、表題の補題を示しておきます。
なにか g:ba×a→b があって、それにΛaを作用させるとbaのidになるなら、gはevalだ、ということです。逆も成立します。
Λ(g) = id ⇒ g = eval :
Λ(g) = id を仮定する。
両辺にΓを作用させ、[1]を使うと
g = Γ(id)
ところが、[2]より Γ(id) = eval だから
g = eval
g = eval ⇒ Λ(g) = id :
g = eval を仮定する。
両辺にΛを作用させると、
Λ(g) = Λ(eval)
ところが、[3]より Λ(eval) = id だから
Λ(g) = id
結局、
- [5] Λ(g) = id ⇔ g = eval
●下ごしらえ
[追記 date="翌日"]「下ごしらえ」って、何の下ごしらえ? かというと; (ina:a→a', outa:a'→a)と(inb:b→b', outb:b'→b)がレトラクト対であるとき、baとb'a'のあいだのレトラクト対を具体的に構成する話です。http://www.cs.unibo.it/~asperti/PAPERS/book.pdfのP.18, 2.3.4。[/追記]
- 左の箱 = (ba×outa);eval;inb
- 右の箱 = (b'a'×ina);eval;outb
として、示すべき等式は次の図の上段の形をしています。
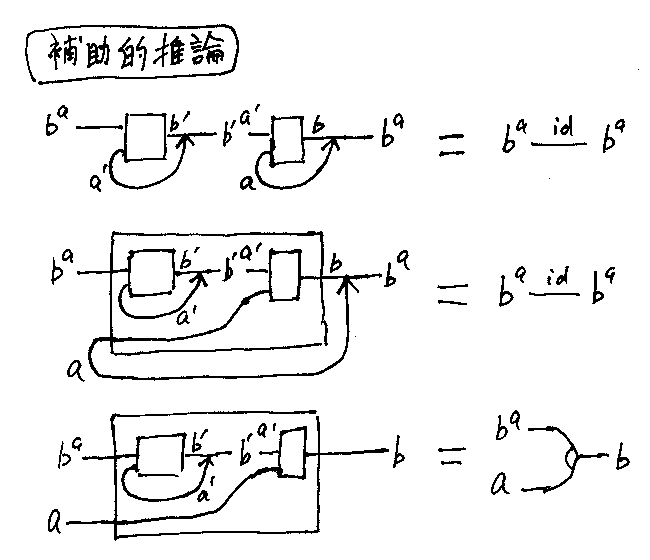
念のため、等式でがんばって書けば:
- [6] Λa'[(ba×outa);eval;inb];Λa[(b'a'×ina);eval;outb] = ba
左タイトニング[4]を使って、右の箱から出ている輪ッコ(ラムダ)を左に向かって引き伸ばせば中段の図になります。中段の図の大きな箱をgだと思って [5] Λ(g) = id ⇔ g = eval を使えば、下段の図と同値になります。
というわけで、下段の等式(↓)を示すことにします。
- [6'] (Λa'[(ba×outa);eval;inb]×a);[(b'a'×ina);eval;outb] = eval
ただし、in;out = id が使えます。
[追記 date="翌日"]in;out = id は、inとoutがレトラクト対になっていることです。レトラクトについては:
- レトラクションの起源(かな?) →http://d.hatena.ne.jp/m-hiyama/20070625/1182733108
- レトラクションとベキ等自己射 →http://d.hatena.ne.jp/m-hiyama/20070627/1182922095
[/追記]
●計算
[6']を絵算で示します。
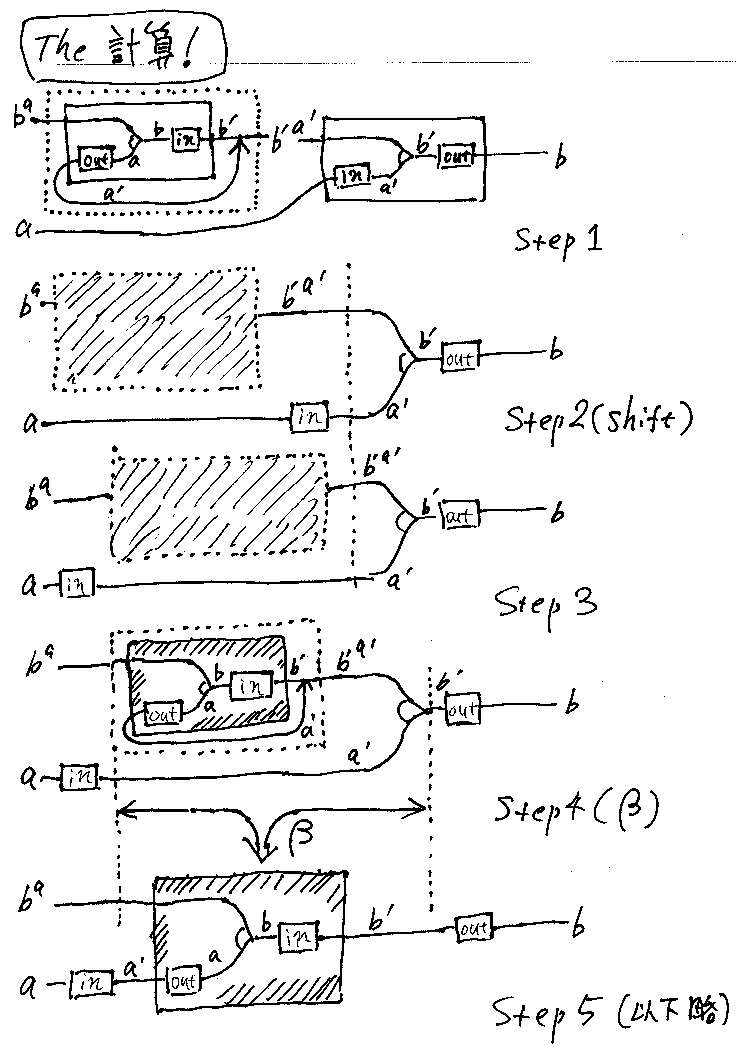
- Step1 -- 上図の点線の箱にベールをかけ(中身が見えると邪魔)、レイアウトを調整。
- Step2 -- ベールがかかった大きな箱と、inと書いてある小さな箱の位置を交換。これはスライディングとかシフトと呼ばれる操作です。等式で書けば (f×id);(id×g) = (id×g);(f×id)。交替律の特殊例です*1。http://www.chimaira.org/docs/Superposing.htm#s6 も参照。
- Step3 -- 特に何もやってません。箱のベールを外しただけ。
- Step4 -- 点線で挟まれた部分にベータ変換。
- Step5以降 -- inとoutが続けて出現しているので、in;out = id を使って消してしまえば、evalだけが残ります。
この絵算を等式計算に翻訳するとコンナ。この等式を先に見せられたら、僕はたぶん追いかけられない。
*1:この特殊例から、逆に一般の交替律を出せます。