久々のお絵描き講座です。10枚の絵を描いたぞ(って、落描きみたいなモンですけど)。
有向グラフは計算科学(コンピューティング・サイエンス)で頻出する大事なデータ構造です。コンピュータで扱えるのは有限グラフですが、無限グラフが登場しないのかというと、そうではありません。コンピュータでも、可能性として無限となりうるデータ構造を扱います。とはいえ、何の秩序もない無限データはさすがに扱いにくいので、有限的に定義できる無限構造が興味の対象となります。
ここでは、無限な有向グラフのなかで最もよく使う無限ツリーを考えます。さらに、次の条件を満たすものを例題に使います。
- 末端のノード(リーフノード)には整数の値が付着している。
- 中間の分岐ノードは特に値を持たない。
絵を描くときは、末端ノードには単に整数だけを書き、中間ノードは黒丸にします。ルートノードを識別するためには、「ルート」とラベルを書いた矢印を使います。次は、有限ツリーを描いた例です。
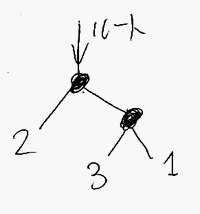
無限二分木
次の図のような無限に続く二分木を考えます。この無限二分木には末端ノードはなくて、すべてのノードが中間ノードです。中間ノードが無限に続きます。
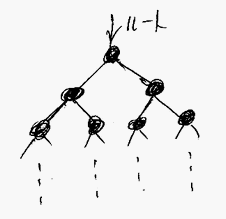
ツリー全体やサブツリーを、A, B,C などの英字大文字で表すことにします。次のような感じです。
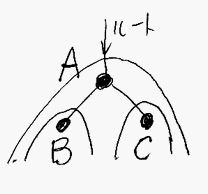
この図とまったく同じことを、テキスト記法では次のように表現しましょう。
A ::= ・(B, C)
これはBNF(バッカス/ナウア形式)の一種です。タプル (B, C) の前に付いている黒丸「・」は、図の「BとCを接合する黒丸」に対応していると思ってください。
今話題にしている無限二分木では、AとBとCが同じ形状のツリーなので、そのBNFは次のように書けます。
A ::= ・(A, A)
定義式の左辺にも左辺にもAが登場するので、これは再帰的な定義です。再帰的な定義は、「可能性としての無限」を導入します。
また、再帰的な無限構造は循環的構造による表現が可能です。無限二分木は、次のような循環的グラフ(サイクルを持つ有向グラフ)で有限的に表すことができます。無限構造だけど「有限的な表現」を持つ点がキモです。
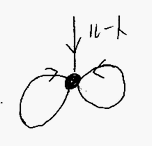
BNFなり循環的グラフなりの有限的な表現を持つ無限ツリーは正規ツリー(regular tree)とか有理ツリー(rational tree)とか呼ばれます。「正規」は正規表現の「正規」です。実際、ツリーがBNFで定義できることは(ツリー用の)正規表現で定義できることと同じです。「有理」は有理数の「有理」と同じです。有理数は少数展開すると無限小数になるかも知れないけど、分数で有限的に表現できるわけで、よく似た概念でしょ。
末端ノードを持つ無限三分木
今度は次の無限ツリーを考えましょう。
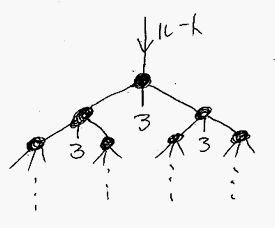
中間ノードから枝が3本出ますが、真ん中の枝は整数3が付着した末端ノードに繋がり終端します。左右の枝は無限に伸びます。
もうあまり説明は要らないでしょう。この無限三分木のBNFは次のとおり。
A ::= ・(A, 3, A)
対応する循環的グラフはこうなります。
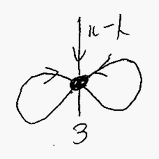
無限に続くリスト
次なる例は下図のものです。
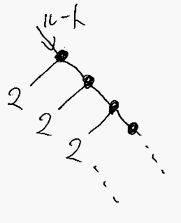
これをLispやSchemeのリストだと思うと、整数値2が無限に並んだリストになります。終端のnilは出てきません(無限の彼方にnilがあると思ってもいいです)。
(2 2 2 2 2 ...)
これのBNFはもはや明らかですね。
A ::= ・(2, A)
対応する循環的グラフも簡単。
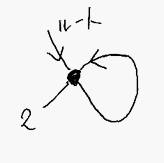
これはどんな無限ツリー?
最後の例はBNFからスタートします。
A ::= ・(2, B) B ::= ・(A, 3)
これは、AとBが相互再帰している再帰的定義です。AとBをそれぞれ独立したツリーとして絵を描くと次のようです。
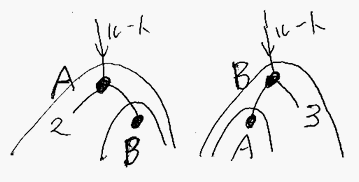
これを繋ぎ合わせて1つの循環的グラフを作るには多少の慣れが必要かも知れません。Aのルートを全体のルートにして、Bをその下にぶら下げることにします。すると、結果の循環的グラフは次のようです。
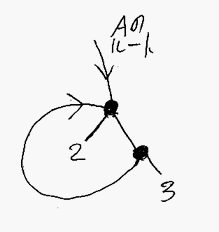
循環的グラフを無限ツリーに展開するのは宿題にしましょう。どんな無限ツリーになるかな?
僕はこういう絵を描くのがほんとに好きなんだけど、スキャンしたり切った張ったが手間なんですよねぇ。頭のなかでは絵図で考えていても、いつもは手からテキスト表現に翻訳している感じ。ブレインスキャンで絵が出てきたりするといいんだけど、、、