双モノイドの簡単な例 -- 自然数の足し算と余足し算

[追記 date="翌日"]絵を入れて、間違いを修正し、少しだけ文言を変えました。[/追記]

エフイチ関係で名前を出したことがあるコンヌ（Alain Connes）やマニン（Yuri Manin）が、最近は計算（computation）やアルゴリズムに興味を持っているようです。場の量子論とかファインマン・グラフなんかと一緒に、原始帰納関数とかルンゲクッタ法とかを話題にしている論文があります。なんだかサッパリ分かりませんわ。でも、道具立てに双代数やホップ代数を使うらしいことは読み取れます。

とりあえず双代数の簡単な例を作ってみようとしたのですが、自明ではなく*1線形代数や群論の知識なしで作れる双代数がなかなか見つかりません。集合圏ではなくて、ベキ集合モナドのクライスリ圏、つまり非決定性写像の圏なら小学校レベルの予備知識で双代数が作れます。自然数（0, 1, 2, ...）の足し算以外は何も使いません。もっとも、舞台をこしらえるのにクライスリ構成とテンソル強度を使うのは、簡単と言っていいかどうか？

やることはホントに簡単なのに、舞台のセットアップを大げさにするのもナンですから、クライスリ圏には言及せずに、非決定性写像（クライスリ射に相当）の直積（クライスリ圏のモノイド積に相当）の具体的な表現だけを使うことにします。この方針なら、たぶんホントに簡単です。

内容：

1. 用語について
2. JavaScriptで概要
3. 非決定性写像
4. 足し算
5. 余足し算
6. 双代数法則

用語について

よく使われる用語は「双代数」（bialgebra）ですが、ここでは「双モノイド」（bimonoid）と呼ぶことにします。「代数」が色々な意味で使われ過ぎて曖昧な感じがするからです。モノイド概念をモノイド圏で相対化すれば、いろいろな代数系を表すことができます。例えば、集合圏 (Set, ×, 1) のモノイドは普通のモノイド（狭義のモノイド）で、K-ベクトル空間の圏 (Vect_K, (×), K) （(×)はテンソル積のつもり）のモノイドはいわゆるK-代数（K-多元環）になります。圏の圏 (Cat, ×, 1) のモノイドはモノイド圏です。そして、自己関手の圏 (End(C), ;, Id) のモノイドはC上のモナドです。（「圏、関手、モナドはどうしたら分かるの？」も参照。）

ここでいう双モノイドは、適当な圏の対象と射の組み合わせで、モノイドと余モノイドの構造を持ち、さらに適当な法則を満たすものです。適当な法則とは双代数法則と呼ばれ*2、次の絵で表現できます。

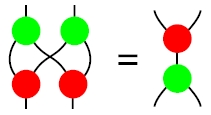
この絵はジョン・バエズ（John Baez）の記事で使われていたものです。色塗るだけできれいに見えますね。

JavaScriptで概要

扱うデータは自然数（非負整数）に限定します。足し算とゼロを関数で書くと次のようです。

function add(n, m) {

 return n + m;

}
function zero() {

  return 0;

}

戻り値を、ひとつの自然数から自然数の集合に変更しましょう。JavaScriptの配列を集合の表現に使うとするなら：

function Add(n, m) {

  return [n + m];

}
function Zero() {

  return [0];

}

「2たす3は5」は足し算ですが、「たしたら5になる2つの数は？」に答えるのが余足し算です。余ゼロは「ゼロ以外は未定義にしてしまう」操作です。それで、余足し算（coaddition）と余ゼロ（cozero）は次のようになります。余足し算の戻り値はネストした配列ですが、外側は集合の表現、内側はペア（長さ2のタプル）の表現です。

function Coadd(n) {

 var r = [];

 for (var i = 0; i <= n; i++) {

  r.push([i, n - i]);

 }

 return r;

}
function Cozero(n) {

  if (n == 0) {

    return [0];

  } else {

    return [];

  }

}

以下では、「足し算、ゼロ、余足し算、余ゼロ」の混じった計算法則について述べます。

非決定性写像

AとBを集合として、Aの各要素に、Bの部分集合（空集合でもよい）を対応付けるような写像を、AからBへの非決定性写像と呼びます。fがAからBへの非決定性写像であることを f:A--*>B と表記することにします。普通の写像（決定性の全域写像）は f:A→B とします。

f:A--*>B, g:B--*>C のとき、fとgの結合f;gは次のように定義されます。h = f;g として：

• h(a) = ∪_b∈f(a)(g(b))

f:A→B に対して、F(a) = {f(a)} で定義される非決定性写像 F:A--*>B を f~ と書くことにします。恒等写像 id_A:A→A に対する (id_A)~ は、混乱がなければ同じ記号 id_A で表すことにします。

すると、f:A--*>B, g:B--*>C, h:C--*>D に対して次が成立します。

1. (f;g);h = f;(g;h)
2. id_A;f = f;id_B = f
3. (f;g)~ = f~;g~
4. (id_A)~ = id_A

f:A--*>B, g:C--*>D のとき f×g:A×C --*> B×D を次のように定義します。

• (f×g)(a, c) = f(a)×g(c) = {(b, d)∈B×D | b ∈f(a) かつ d∈g(c)}

f, gが普通の写像のときは、(f×g)(a, c) = (f(a), b(c)) なので、次も成立します。

• (f×g)~ = f~ × g~

足し算

ゼロを含む自然数全体の集合をNとします。足し算は、+;N×N→N という写像ですが、+~ :N×N--*>N を以下∇と書きます。∇(n, m) = {n+m} となります。特定された単元集合を 1= {0} として、η(0) = {0} で定義される非決定写像 η:1--*>N も考えます。ηは足し算の単位、つまり定数ゼロに対応する射です。

足し算の結合律と左右の単位律は次のように書けます。idはid_Nのこと、ρはNと1×Nの同型を与える非決定性写像、ρ(n) = {(0, n)} です。ρ'は、ρ'(n) = {(n, 0)} となります。（ρ:N--*>1×N、ρ':N--*>N×1）

1. (∇×id);∇ = (id×∇);∇
2. ρ;(η×id);∇ = id
3. ρ';(id×η);∇ = id

絵で描くと次のような感じ。（[追記 date="翌日"]ρとρ'の箱の位置がずれてるけど、描き直すのめんどいから、カンベンして。点線の箱を少し上に移動したほうが正確な図。[/追記]）

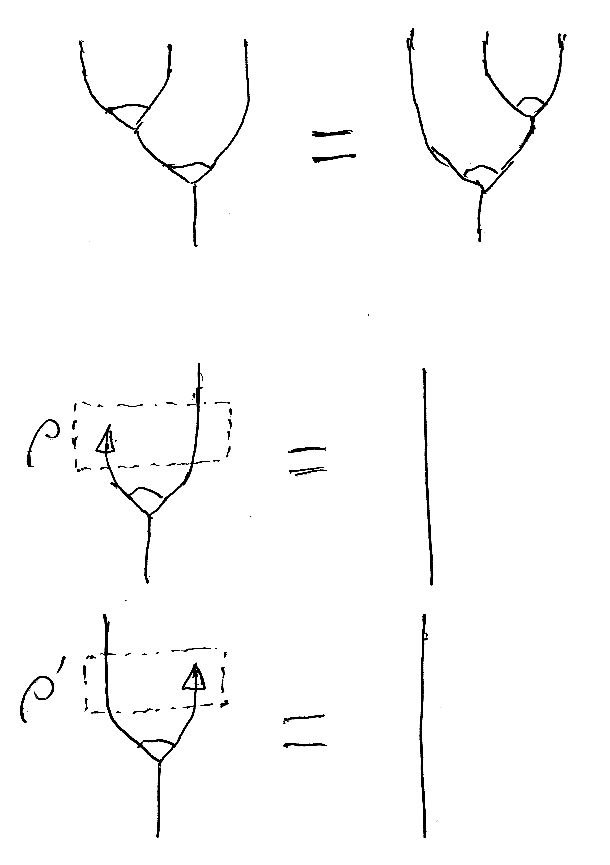
余足し算

足し算の双対を定義しましょう。ここで初めて非決定性写像の本領発揮です。通常の写像の範囲では、余足し算（足し算の双対）がうまく定義できません。余足し算（coaddition）は、Δ:N--*>N×N という非決定性写像です。つまり、ひとつの自然数に対して、自然数のペアから構成される集合を対応させます。その定義は以下のとおり。

• Δ(n) = {(s, t)∈N×N | s + t = n}

余足し算のいくつかの実例：

1. Δ(0) = {(0, 0)}
2. Δ(1) = {(0, 1), (1, 0)}
3. Δ(2) = {(0, 2), (1, 1), (2, 0)}
4. Δ(3) = {(0, 3), (1, 2), (2, 1), (3, 0)}

Firebugのコンソールなら：

>>> Coadd(0)

[[0, 0]]

>>> Coadd(1)

[[0, 1], [1, 0]]

>>> Coadd(2)

[[0, 2], [1, 1], [2, 0]]

>>> Coadd(3)

[[0, 3], [1, 2], [2, 1], [3, 0]]

>>> Coadd(4)

[[0, 4], [1, 3], [2, 2], [3, 1], [4, 0]]

Δ;∇ = id となることはすぐに確認できるでしょう。Δに関して、結合律、単位律の双対である余結合律、余単位律が成立します。このことをハッキリと述べるには余足し算の余単位、つまり余ゼロ（cozero）の概念が必要です。余ゼロεを次のように定義します。

• ε(0) = {0}
• n≠0 ならば ε(n) = {} （空集合）

余結合律、左余単位律、右余単位律は次の等式です。

1. Δ;(Δ×id) = Δ;(id×Δ)
2. Δ;(ε×id);ρ^-1 = id
3. Δ;(id×ε);ρ'^-1 = id

ここで、ρ^-1:1×N--*>N と ρ'^-1:N×1--*>N は次のように定義されます。

• ρ^-1(0, m) = {m}
• ρ'^-1(n, 0) = {n}

「余」が付いた計算法則を絵で描くと次のような感じ。（[追記 date="翌日"]ρ^-1とρ'^-1の箱の位置がずれてるけど、描き直すのめんどいから、カンベンして。点線の箱を少し下に移動したほうが正確な図。[/追記]）

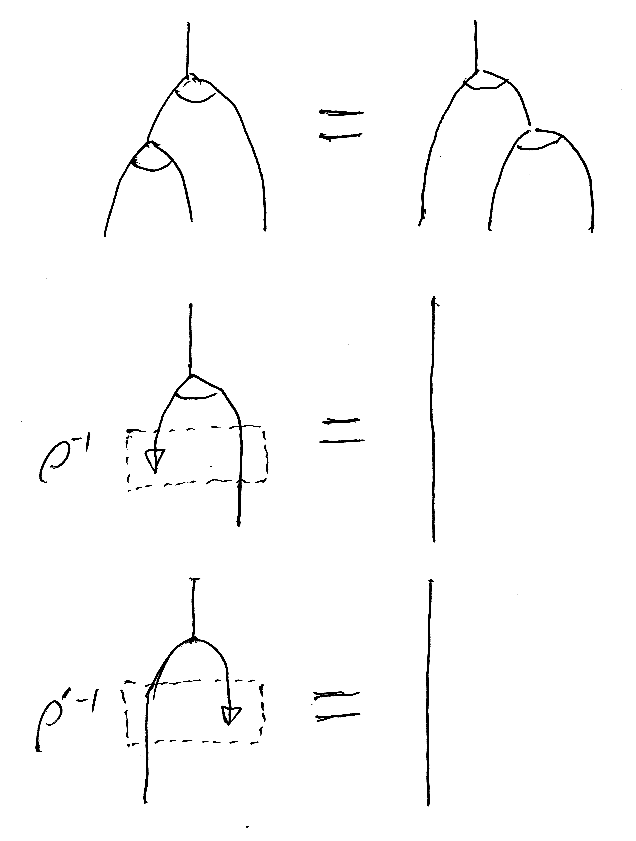
双代数法則

今までの定義により自然数は、「足し算とゼロ」でモノイド、「余足し算、余ゼロ」で余モノイドになります。ただし、単なる写像じゃなくて非決定性写像で考えてのことです。モノイド演算と余モノイド演算を混ぜて使ったときにどのような事が起こるかを支配する法則が双代数法則です。

双代数法則を述べるには、ゼロと余ゼロを少しだけ一般化しておくと便利です。η₂:N--*>N×N と ε₂:N×N--*>Nを次のように定義します。

• η₂(0) = {(0, 0)}
• ε₂(0, 0) = {0}、n≠0 または m≠0 ならば ε₂(n, m) = {} （空集合）

双代数法則とは、次の等式群です。

1. ∇;Δ = (Δ×Δ);(id×σ×id);(∇×∇)
2. η;Δ = η₂
3. ∇;ε = ε₂

最初の法則は、冒頭で挙げた絵が表すものです（等号の左右が絵と逆ですが）。上から下の方向に見るとして、赤玉が∇、緑玉がΔに対応します。(id×σ×id) は、長さ4のタプルの中央の2つの項目を入れ替える写像です。

双代数法則の定義を追いかけて具体的に書き下すと、その主張はホントに小学校のレベルです。それでも、「えっ、こんなことが成り立っていたのかぁ」と新鮮な気分がするかもしれません。やってみてくださいな。

*1:自明な例なら、対角を余乗法とする双代数があります。

*2:広く認知された名前はないようです。代数かつ余代数（モノイドかつ余モノイド）が双代数になるための条件という形で引用される法則です。