「物理と情報と幾何のインフォーマルかもな勉強会 @渋谷」より:
僕(檜山)も「クリーネスター・圏論・計算の離散力学」というお題でナニカしゃべります。内容が固まったら、案内に書いてあるより詳しいことを書くつもりです。
以下に「より詳しいこと」を書きます。僕は当日の資料を作らないので、このエントリーが資料代わりです。
と言うと、僕が怠けて準備をしないように思えるかもしれませんが、そんなことはありません。ネタとストーリーは色々考えているし、リハーサルもします。リハーサルとは、一連の絵を描く練習ですね。これらの絵を資料にすることは、アニメーションのセル画一式を準備するようなもんで、とても出来やしないのですよ。
僕の話では、クリーネスターが主人公、いやむしろ狂言回しを演じます。異なった分野の色々な場面でクリーネスターが登場します。それらのクリーネスター達を理解したい/具体的に計算したい、それが今回の話の動機/テーマです。
このテーマを、主に次の4つの観点から眺めてみようと思います。
これら4つの観点を、それぞれノート1枚にメモしたので、ここでそれを紹介します。メモ・ノートはないのですが、このエントリーの最後に、アルゴリズムの話を補足します。
登録はアテンドで:
行列線形代数
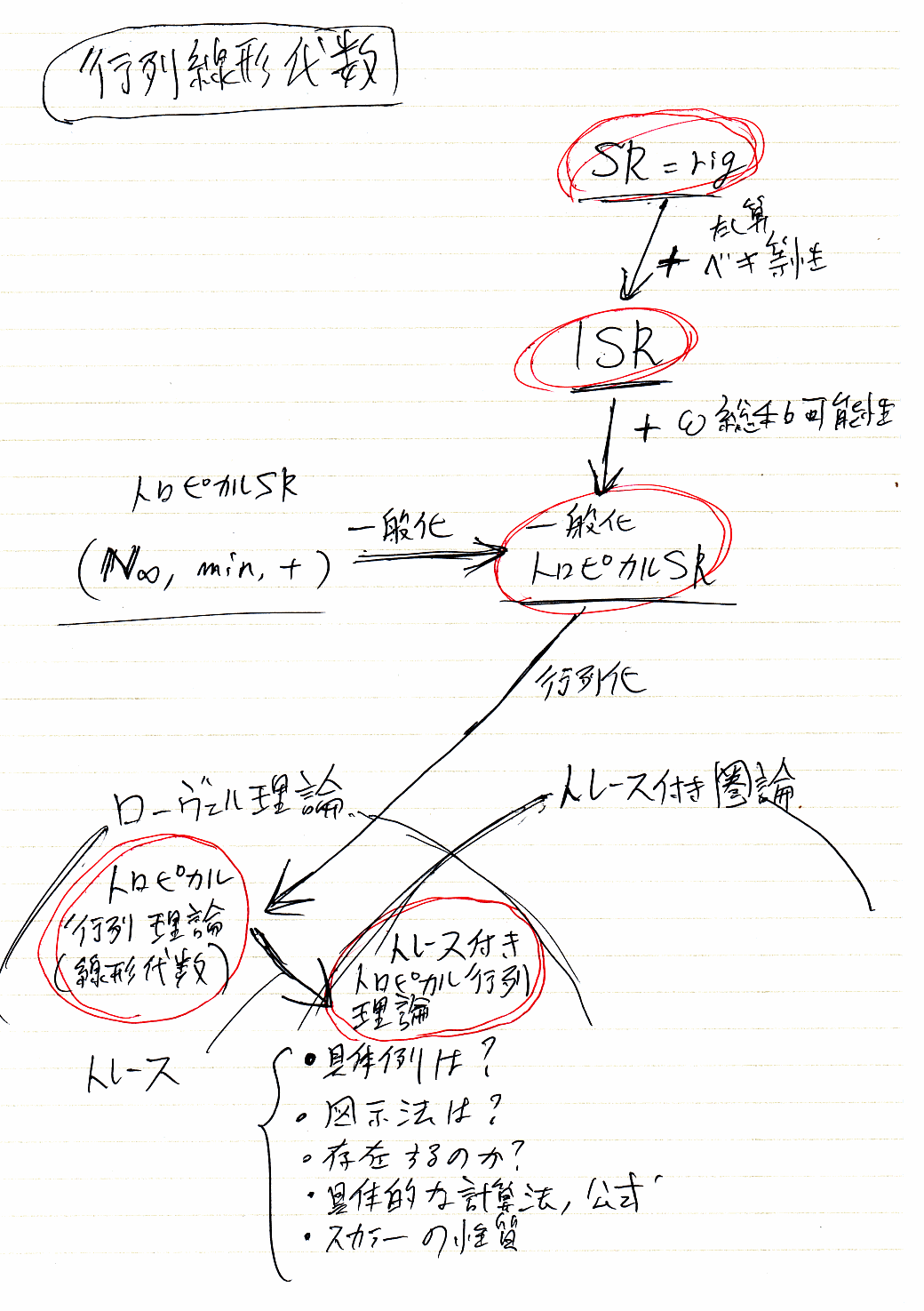
線形(線型)代数とは言っても、ベクトル空間や線形写像のような抽象的な枠組は使わないで、行列の計算を露骨(explicit)にします。足し算と掛け算だけを使う行列計算です。でも、係数域が少しエキゾチックで、ベキ等半環(idempotent semiring; ISR)をスカラーの代数系とします*1。
ベキ等半環の簡単で面白い例として、N∞ = N∪{∞} = {0, 1, 2, ..., ∞} に、minを加法、+を乗法として演算を入れた (N∞, min, +) があります。これは、トロピカル半環(あるいは、トロピカル環、トロピカル代数)と呼ばれます。NをR(実数)に置き換えたり、minの代わりにmaxを使ったりして、色々な変種を定義できます。これらを総称して(広義の)トロピカル半環と呼ぶこともあります。
具体的なトロピカル半環を、無限和が意味を持つような(ω-総和可能な)ベキ等半環まで一般化しても、かなりの結果が成立します。この一般化により、形式言語の代数も射程におさめる事ができます。クリーネスターの故郷は、形式言語の代数的理論なのでした。
係数域がなんであっても、行列の理論はローヴェル(代数)理論(Lawvere (algebraic) theory)になります。ローヴェル理論とは、対象が自然数(非負整数)、直積が足し算で与えられるような圏で表現できる計算体系のことです。行列の場合はさらに、直和も足し算で与えられることになります。
行列計算のなかで、直接にクリーネスターを扱うこともできますが、より自然で豊かな結果をもたらすと思える方法は、トレース付き圏を使う方法です。
トレース付き圏論
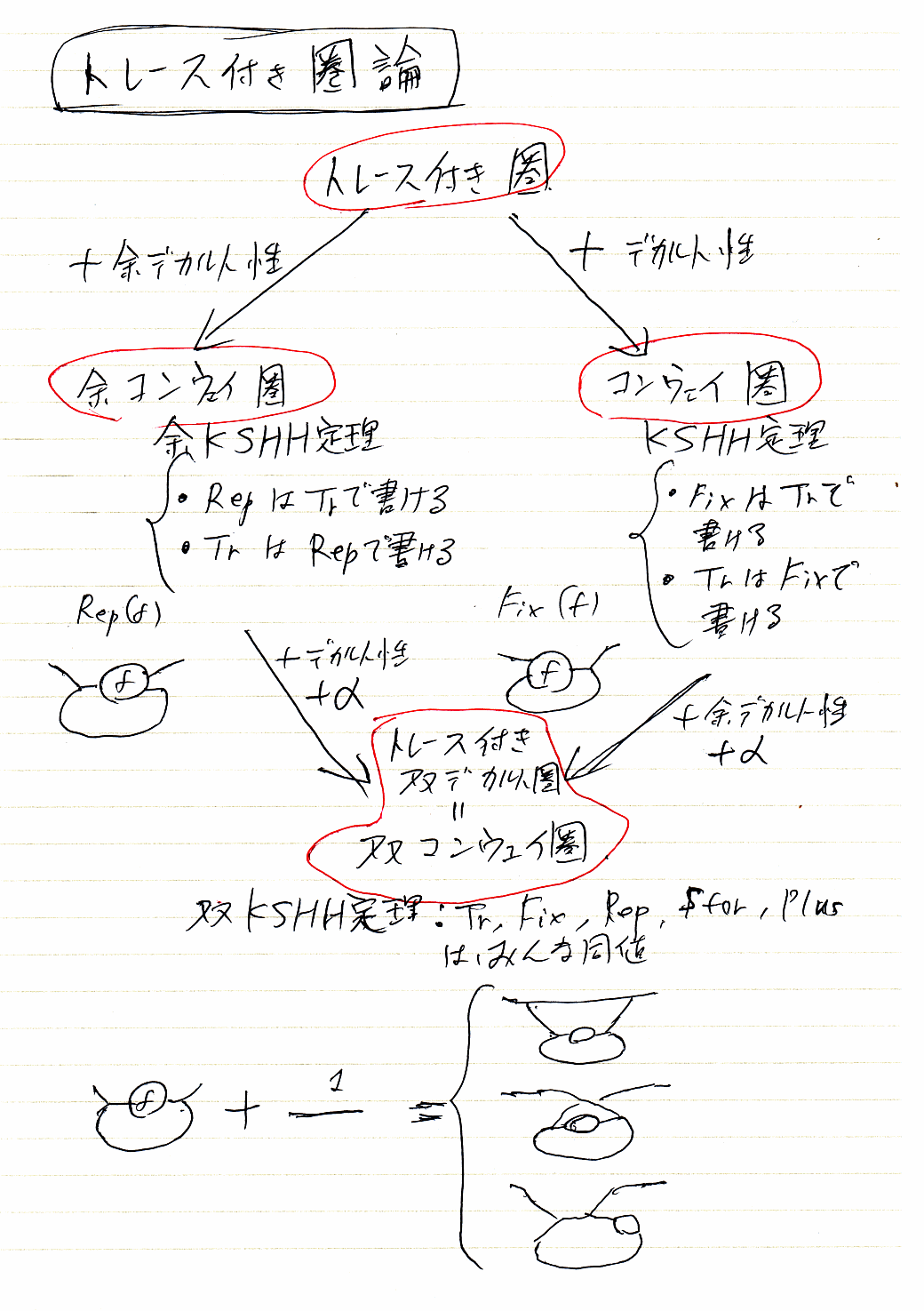
トレース付き圏(トレース付きモノイド圏)は、その図形的な表示法から、結び目、組み紐(ブレイド)、絡みからみもつれ紐(タングル)*2などと密接に関連するものです。不思議なことに、計算科学、物理、論理などにもトレース付き圏が頻繁に登場します。トレース付き圏については、次の記事で簡単に紹介しています。
トレース付き圏のモノイド積を特にデカルト積にしたものがコンウェイ圏です。コンウェイ圏のもともとの定義は、トレースを使うのではなくて、コンウェイ不動点演算子を使います。つまり、圏論的に定式化された不動点演算子*3を持つデカルト圏がコンウェイ圏です。
カザネスク/ステファネスク/ハイランド/長谷川の定理(KSHH定理)により、トレースと不動点演算子の構造が同値であることが分かるので、「不動点演算子を持つデカルト圏 = トレースを持つデカルト圏 = コンウェイ圏」となります。
双対的に、余不動点演算子を持つ余デカルト圏を考えると、これはトレースを持つ余デカルト圏と同じことになります。トレースは自己双対的な概念なので、余トレースとトレースを区別する必要はありません。余不動点演算子を持つ余デカルト圏(=トレースを持つ余デカルト圏)を余コンウェイ圏と呼ぶことにします。
余不動点演算子は、エルゴット繰り返し演算子と呼ばれることもあり、非決定性プログラムのルーピングの挙動を記述するために使われたりします。コンウェイ圏と余コンウェイ圏の双対性は、再帰的データ構造と繰り返しプログラムの双対性を暗示しているようですが、僕はハッキリとは把握してません。
さて、デカルトかつ余デカルトであり、しかも互いに双対なデカルト構造が“調和”しているような圏を考えます。そのような圏は、デカルト双積(cartesian biproduct)を持つ圏です -- 双デカルト圏と呼びましょう。行列の圏は双デカルト圏になります。
双デカルト圏にトレースを入れると、トレース付き双デカルト圏=双コンウェイ圏となります。トレースが付いた行列計算を展開するにふさわしい場は双コンウェイ圏です。実際、双コンウェイ圏の一般論から、具体的な行列計算の公式やスカラーの性質*4などがワラワラと出てきます。クリーネスターもトレースから計算できること、また逆にクリーネスターからトレースや不動点演算子が定義可能なことも(KSHH定理から)分かります。
力学

力学系とは、運動などの現象を、空間変数xと時間変数tに対して、x' = F(x, t) のような方程式で記述したものです。ここで、x' は時間微分(連続時間のとき)と考えても、次の位置(離散時間のとき)と考えてもかまいません。
F(x, t) が時間発展の法則を与えますが、Fが時間によらないときは自律的力学系(自律系)となります。ここでいう自律的とは(語感の印象と違うかもしれませんが)、時間に沿ったナニカの変化(例えば運動)があって、その変化を記述する法則のほうはずっと変わらないことです。
自律系の場合の方程式は、x' = F(x) となります。このときのFは、xの変域である空間X上のベクトル場だと思っていいでしょう。時間が離散的な場合は、Fは単なる写像 X→X で代用できます。つまり、離散時間自律系はXの自己写像に過ぎません。一般の圏においても、対象Xの自己射(endomorphism)Fとして定義できます -- これ重要です。
自律的力学系の生成子Fに対して、U(t) = Exp(F, t) とします。ここでExpは“指数”ですが、指数的なナニカを象徴的に表しています。ExpによってFから作られたUは、指数法則を満たすべきだ、ってことです。Uは時間推移に伴う系の発展を記述する作用素です。
自律系Fの長時間に渡る(時間的マクロな)挙動を調べるために、無限の未来の状態 U(∞) が求まるとうれしいです。タチの良いFならば、U(∞) = Exp(F, ∞) が求まります。U(∞) は、時間発展の途中の経緯を捨ててしまいますが(場合によっては捨てないで蓄積する)、系が終局的にどうなるかを知っています。終局的な状態は、安定点、平衡点(equilibrium)、停留点、極値、シンク、極限点、閉包などと呼ばれることがあります。これは、離散的変分法や逐次近似とも関係します。
離散時間の自律的力学系を、双コンウェイ圏で考えたらどうなるでしょうか。双コンウェイ圏の射 F:X→X を生成子とする力学系に対して、その終局的状態(を与える作用素)U(∞) = Exp(F, ∞) が求まるか? ということです。また、例えば粒子の軌道のような力学的アナロジーがどこまで通用するかも興味深い問題です。
幾何
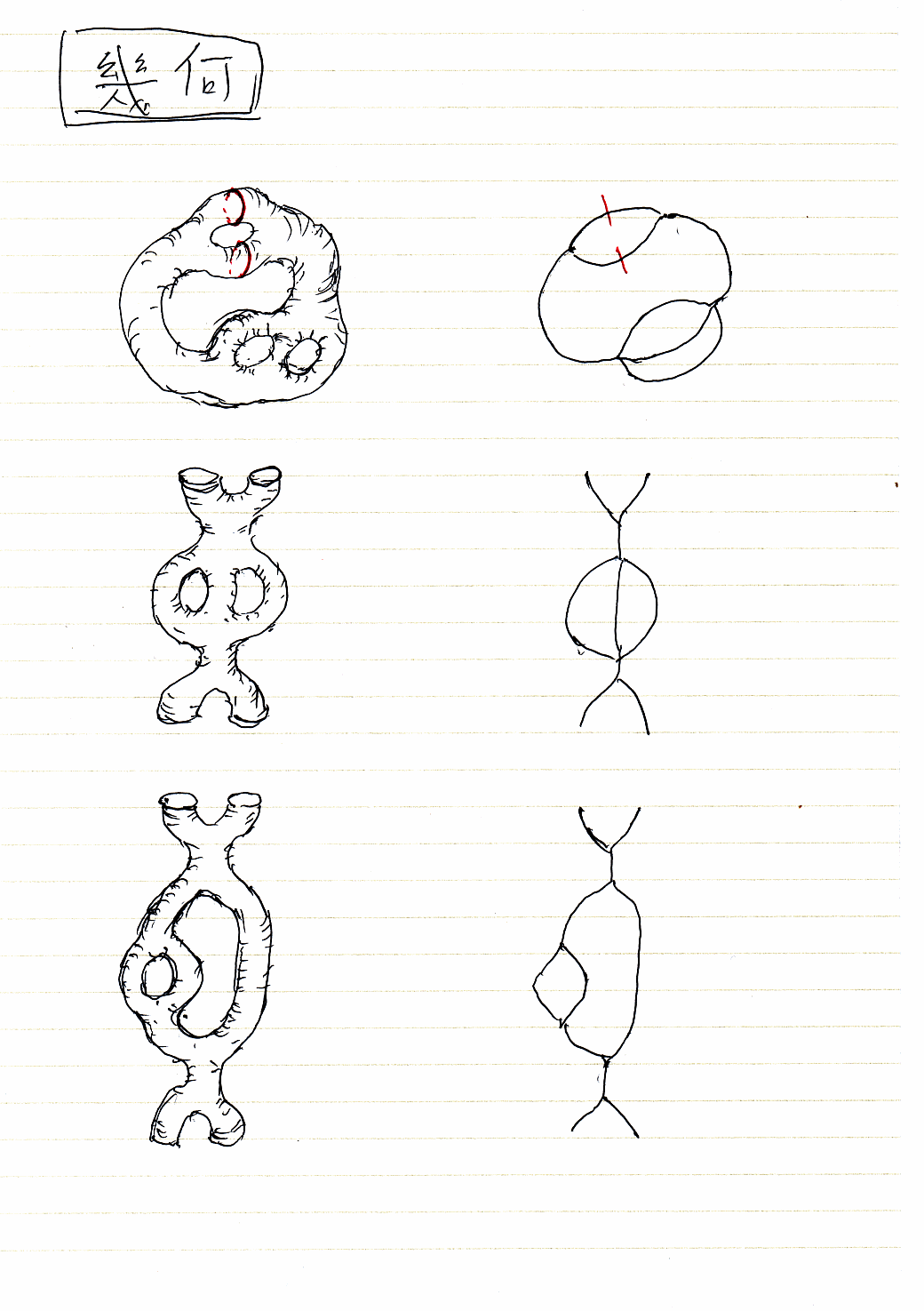
トレース付き圏が幾何的描像を持つので、今までの話は、何かしら図形的な表示が可能です。しかしそれとは別に(別じゃないのかも知れないけど)、行列の計算と力学系のアナロジーの背後には、境界や角(かど)を持つ図形の切り貼りの圏が在るように思えます。
境界や角を持つ図形の切り貼りの圏はコボルディズム圏と呼ばれますが、通常のコボルディズム圏は次元や滑らかさの制約を受けます。もっとゆるくてイイカゲンな圏でもいいんじゃないか、と思ったりします。
とはいっても、「思ったりする」以上には何もワカラズ、すごく曖昧な話です。ヒントになるかもしれない事例をひとつ挙げるだけにします。
左上の絵は、トーラスに穴を3つ開けたもの(のつもり)です。もともとあった穴を入れると4つの穴で、4人乗りの浮き袋に例えられたりします。この浮き袋をジョキジョキとハサミで切ります。赤い線が切り開く場所です。すぐ下に切り開いて伸ばした状態。その下に少し変形した状態を描いています。
右側の列は、浮き袋のような2次元図形ではなくて、線図(グラフ)です。赤い切り取り線のところで切って、伸ばしたり変形したりしているのは同じです。
右側の線図は、左側の浮き袋の内部に“中心線”を描くと得られます。通常、2次元の面を離散近似するには、三角形などの多角形に分割します。が、次元も落としてしまっても近似の役割を果たすときがあります。左側の図形が、中空の浮き袋ではなくてソリッドならどうでしょう? 例えば粘土をこねて作った塊とか。そうすると、右側の線図は3次元図形の1次元近似になります。
インフォーマルな絵算(pictorial/graphical/diagrammatic calculation)をフォーマルにしようとするとき、次元だの滑らかさだの特異点だのを気にしているとうるさ過ぎる気がするのです。そういう違いを捨象するような同値性があるといいのですが、……、高次圏のホモトピーでしょうか? ヨクワカリマセン。
アルゴリズム、その他
双コンウェイ圏のなかでトレース/不動点/クリーネスターを行列として具体的に計算するとき、いくつかの行列(同じ行列がたくさんでもいい)をすべて掛け合わる「総積」の公式が必要です。この公式は、行列の掛け算そのものなんですが、力学(離散自律力学系)とのアナロジーで眺め直してみるとけっこう面白いものです。
総積、特にベキ乗の計算は、最短経路問題などと同値になります。ここで、ウォーシャル/フロイド法、ダイクストラ法、ベルマン/フォード法などのアルゴリズムと関係してきます。
最初は、これらのアルゴリズムの背景として力学的解釈を説明しようと思っていたのですが、1時間程度だと無理でしょうね。簡単に触れる程度、それさえも出来ないかもしれません。
でも、総積(双積ではない)を求める公式は、いろいろな解釈ができて妄想が広がるので紹介したいと思います。