このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

2の補数は分かりにくい、こう考えれば分かる

雑記／備忘

現代のコンピュータでは、負の数の表現に「2の補数」を使っています。「2の補数」って何だよ？ 改めて調べてみると、説明（例えばWikipedia）が分かりにくいですね。だいたい分かっても、「それが何なの？」という感じ。

「2の補数」はコンピュータと2進数の文脈で語られるけど（実際、それはそうなんだけど）、ことの本質はそこじゃない、「ビットを反転して1を足す」とか呪文ように覚えても全くショーモナイ。むしろ、「コンピュータ」や「2進数」から離れたほうがいいんじゃないか、とさえ思えます。

時計や角度とのアナロジーや循環（ラップアラウンド）を含んだ説明がないかと探していたら、2008年の自分の記事がひっかかりました。

こんなこと書いたの、もうすっかり忘れていたわ。まー、いいこと書いてあるんだけど :-) 「2の補数」が幾つかのトピックのひとつになっています。ここでは「2の補数」の一般的背景を主題的に扱います。ただし、「コンピュータ」と「2進数」は強調しません。固定された有限個の記号しかない状況での、表現と演算の問題にフォーカスします。コンピュータに関する注意は最後の補足で触れます。

僕が言いたいことを手っ取り早く知るには、一番最後「どんな仕掛けか」にある手描きの絵を見てもらえればいいかと思います。

内容：

限られた記号

決まった個数の記号しかないときに、その記号をやりくりして整数を表現すること、足し算を行うことを考えます。それがテーマです。このテーマは一般的なもので、それを特定状況に適用すると「2の補数」の話になります。

数字（digit）としては、ごく常識的に「0, 1, 2, 3, 4, 5, 6, 7, 8, 9」の10個を使うとします。ただし、数字の並びは3桁までとします。80や753はいいですが、3141はダメです。1000以上はアウトです。

この制限内だと、0から999までの千個の整数を表現できます。整数1000（4桁だ！）は表現できませんが、0が入るので、0〜999 の整数の個数は千個です。

今述べた制限を保ちながら、

  1. 足し算をどうするか？
  2. 負の整数をどう表現するか？

という問題を考えます。

足し算は時計方式

「10個の数字を最大3桁まで」の制限内では、0〜999 の整数しか表現できません。500 + 400 を計算した答は 900 なのでいいのですが、500 + 600 の答を表現するスベがありません。どうしたもんでしょう？

ひとつの案は、計算した結果が999を超えてしまったら999にしてしまう、という方法です。999を（正の）無限大とみなすわけです。実際にこの方法は使われています。（「「イチ、ニ、サン、イッパイ」の算数と分配代数」に関連する話題があります。）

ここでは、別の方法を紹介します。時計方式の足し算です。アナログの時計盤を思い起こしてください。でも、次のような時計盤はやめましょう。


[画像は http://www.boredpanda.com/cool-and-creative-clocks/ より拝借]。

次のような素直な時計盤を想定します。


[画像は http://www.oboeyo.com/pc-memo2/2012/06/19/ より拝借]

時計では、12時 = 0時 なので、12 = 0 という等式を認めることにします。すると、9 + 4 = 1 になります。なぜなら、9 + 4 は普通に計算して13ですが、13 = 12 + 1 = 0 + 1 = 1 です。午前9時から4時間たったら午後1時なので、それほどの違和感はないでしょう。

計算結果が12なら0として、12を超えてしまったら「12で割った余り」を答にします。そうすれば、足し算（掛け算でも）の結果は、0〜11 であることが保証されます。

0〜999 の範囲での計算でも同様な原理を適用して、計算結果が1000なら0として、1000を超えてしまったら「1000で割った余り」を答にします。例えば、500 + 600 = 100 ですね。ここから先、足し算はこの方式を採用します。

実は、この時計方式の計算はコンピュータで使われています。それを実験した画面を「循環を巡る話」から引用しましょう。

0
1
2
3
... (省略)
253
254
255
0  ←注目
1
2
3
... (省略)
41
42
43

この例は、0〜255 の範囲（8ビット符号なし整数）の話。1ずつ増やしていくと、255の次が0になります。256 = 0 です。0から255までの目盛りが付いている時計による計算になっています。

負の整数を表す準備

通常、負の数を表すにはマイナス記号「-」を使います。もし、「3桁まで」の制限でマイナス記号を使うとどうなるのでしょう。負の数は、-1から-99までしか表せません。マイナス記号も1文字（1桁）に勘定しますから。

正の整数は最大値999で、負の整数の最小値は-99ってバランス悪すぎです。それにそもそも、マイナス記号を使っていいとは言ってません。最初の規則通りに「0, 1, 2, 3, 4, 5, 6, 7, 8, 9」の10個の数字しか使えないとしたら、負の整数をどう表せばいいでしょうか？

無理？ 普通に考えたら無理なんですよ。だから、トリックを使います。このトリックの仕掛けはかなり難しいと思います。「2の補数」の話では、難しいトリックがサラリと説明されているのですが、ここには、記号による計算の本質的な構造が含まれています。それは、「表現と値の関係性」です。

コンピュータやプログラミング言語に慣れていると、「表現と値の区別」、「表現と値の同一視」、「表現と値の相互入れ替え」を無意識にうまく行えます。でも、これ、ほんとうに難しいと思いますよ。だから、くどい説明も必要でしょう。

さて、いままで、「最大3桁までの数字の並び」と「概念としての整数」を特に区別しませんでした。しかし、この2つは別なんです。その点を強調するために、数字の並びによる表現には "500" のようにダブルクォートを付け（文字列とみなし）ます。さらに表現は、必要なら「0」を付け加えてキッチリ3桁に揃えることにします。概念的・数学的な整数は今までどおり 500 のように書きます。

xが表現のとき、xの値は value(x) と書くことにします。value("500") = 500 です。念の為に、valueと、その逆（値から表現を作る）をJavaScriptの関数にしておきます。なお、このプログラムが分からなくても本筋には影響しません。

/* 正しい表現の定義 */
function isValidRepres(x) {
    return true &&
	// 文字列であり、
	typeof x === 'string' &&
	// 長さが3であり、
	x.length === 3 &&
	// 数字（digit）だけからなる。
	/^\d+$/.test(x)
}

/* 正しい表現かどうかのチェック */
function checkRepres(x) {
    if (!isValidRepres(x)) throw "Invalid Representation"
}

/* 表現から値を求める */
function value(rep) {
    checkRepres(rep)
    return 1 * rep;
}

/* 正しい値の定義 */
function isValidValue(x) {
    return true &&
	// 数値であり、
	typeof x === 'number' &&
	// 整数であり、
	Math.ceil(x) === x &&
	// 0以上であり、
	0 <= x &&
	// 999以下である。
	x <= 999
}

/* 正しい値かどうかのチェック */
function checkValue(x) {
    if (!isValidValue(x)) throw "Invalid Value"
}

/* 値から表現を求める */
function repres(val) {
    checkValue(val)
    return "" + val;
}

半分は負の整数とする

「3桁の数字の並び」で負の整数を表す工夫を続けます。使える記号表現は、総数1000個で変更できません。この制限はどうにもなりません。使える記号（3桁の並びで1個の記号と勘定する）の一部を、負の数に割り当てるしかないのです。

正負を半々にすればいいでしょう。従来の大きい数（"501"から"999"）を負の数に割り当てます。
"999"を-1、
"998"を-2、
"997"を-3、
…、
"502"を-498、
"501"を-499
と解釈します。奇妙に思えますか？ また時計を思い起こしてください。12時と0時は一致します。0時、1時、2時、3時、と時計回りに進みます。0時、-1時、-2時、-3時、と時計の文字盤上で逆方向に進みたいなら、0時から反時計回り（左回り）に進むことになるでしょう。そして、12時 = 0時、11時 = -1時、10時 = -2時、9時 = -3時、と勘定するのが自然です。同様に、円周の12等分の代わりに円周の1000等分をして反時計回りに進めば、1000 = 0, 999 = -1, 998 = -2, 997 = -3、と勘定するのが自然なのです。

1000等分の円周で見たとき、0の反対側の点を500とするか-500とするかの選択があります。別にどっちでもいいんです。ちょっとした理由から（この理由は最後に触れます）、-500にします。正の整数が499個、負の整数が500個、それとゼロとなります。

新しい約束のもとで、記号表現と整数値の対応は次のようになります。

/* 負の整数も表現できるようにする
 * 従来の500以上の値は負とみなす
 */
function value2(rep) {
    // いったん、従来方式で値を求める
    var val = value(rep);
    if (val < 500) {
	// そのまま
	return val;
    } else {
	// 1000から引いて、符号を反転
	return -(1000 - val)
    }
}

この関数を実行してみると、次のようになります。 

> value2("999")
  -1
> value2("998")
  -2
> value2("501")
  -499
> value2("500")
  -500
> value2("499")
  499

2つの解釈と足し算

「3桁の数字の並び」という記号表現は、総数1000個です。これはもう固定されています。その記号表現に対して、我々は2つの解釈を与えました。ひとつは常識通りの解釈。もうひとつは、大きい数（正確には、“通常は大きいとされる数”）を負の整数とみなす解釈です。最初の解釈を正整数解釈、ニ番目の解釈を正負整数解釈と呼ぶことにします。

もう一度いくつかの例を挙げれば：

記号表現 正整数解釈の値 正負整数解釈の値
"000" 0 0
"499" 499 499
"500" 500 -500
"501" 501 -499
"998" 998 -2
"999" 999 -1

それぞれの解釈における値の範囲は次のとおり。

正整数解釈 正負整数解釈
最小値 0 -500
最小値の表現 "000" "500"
最大値 999 499
最大値の表現 "999" "499"

今、目の前に1つの記号表現、例えば"600"と出されたとき、その値はハッキリしません。2通りの解釈があるからです。そこで、正整数解釈を前提にするときは u"600"、正負整数解釈を前提とするときは i"600" と書くことにします。uはunsigned（負符号が付くことはない）、iはinteger（正負両方がある整数）のつもりです。u"500" + u"600" = u"100" （足し算は時計方式）とか、i"100" = u"100" とかの意味は明らかでしょう。

ここで注目すべき事実があります。u"500" + u"600" = u"100" は、“1000等分された円周＝矢鱈に細かい時計盤”をイメージすれば分かるでしょう。では、uをiに置き換えた、i"500" + i"600" = i"100" はどうでしょうか？ 実は成立します。

一般に、uを付けた計算等式、例えば u"500" + u"600" = u"100" のuを一斉にiに置き換えてもやはり成立します。いくつかの例で試してください。

  • u"900" + u"100" = u"000"、i"900" + i"100" = u"000"
  • i"999" + i"998" = i"997"、u"999" + u"998" = u"997"
  • u"500" + u"001" = u"501"、i"500" + i"001" = i"501"

uを付けてもiを付けても関係ない、ということは、実は解釈と無関係に記号表現だけで足し算は出来る、ということです。u（正整数解釈）でもi（正負整数解釈）でも、計算メカニズムは一種類しかないのです。

これは何を意味するかというと、「解釈なんて無視して、記号表現と計算メカニズムが直接結びついても何の不都合もない」ということです。コンピュータの話としては、概念的・数学的整数なんて解釈を思い描くのは人間だけで、ビット列信号と加算回路は、そんな解釈なしで勝手に動いて答を出している、ということです。

引き算はどうなの？

以上は足し算の話でした。引き算はどうでしょう。引き算は、符号反転（プラスマイナスの入れ替え）と足し算で実行できます。a - b = a + (-b) です。

ここでまた、時計盤をイメージします。正負整数解釈だと、正の整数が時計盤の右半分、負の整数が左半分に配置されます。符号反転は、左右対称な位置への鏡映変換になります。左右対称変換は、正整数解釈でも考えられます。例えば、u"001"はu"999"に変換され、u"100"はu"900"、u"300"はu"700"に変換されます。

符号反転ではなくて、時計盤での左右対称の鏡映変換なら、正整数解釈／正負整数解釈に関わりなく時計盤（円周）上で考えることができます。これを、flip(u"001") = u"999"、flip(i"501") = i"499" のように書きましょう。少し試してみるとわかるように、flipの効果も、uとiに無関係です。

次の事実が分かりました。

  • 時計方式の足し算は、正整数解釈／正負整数解釈と無関係である。
  • 時計方式の鏡映変換は、正整数解釈／正負整数解釈と無関係である。
  • 正負整数解釈では、引き算は鏡映変換（符号反転に対応）と足し算の組合せである。

となると、「正負整数解釈では」が余計ではないかと見当が付きます。つまり、

  • 正整数解釈でも、引き算は鏡映変換と足し算の組合せである。

が予測され、結局は次のようではないか。

  • 時計方式の引き算は、正整数解釈／正負整数解釈と無関係である。

実験と確認をしてみてください。「循環を巡る話：螺旋、時計、2の補数表現、角度算、リング」も参照。

補足1： 2の補数のこと

10進数（整数の10進表現）をベースに話をしましたが、2進数（整数の2進表現）でも同様な事実が成立します。

3桁の数字列である記号の総数は103 = 1000 個でしたが、8ビットのビット列である記号（コンピュータが扱うデータ）の総数は28 = 256 個です。一般に、基本記号の数はn個、桁数（表現の幅）がkのとき、nk個の記号が使えます。足し算／引き算は、0〜nk-1 または -nk-1〜2k-1-1 の範囲内で行うことになります。

n, kが何であっても一般論は同じです。n = 2（2進数）の場合に特有な事情として、最上位ビットが0か1かで表現（ビット列）を二種に分類できます。この分類を整数値の正負に対応付けると都合がいいので、負の数が1個多くなっています。この点は「Signed Integer (2の補数と剰余の円環)」の解説が詳しいです。

それと、n = 2（2進数）の場合の左右対称の鏡映変換は、ハードウェア的に比較的楽に出来て、それが「ビットを反転して1を足す」操作です。

「2の補数」という言い方はかなりミスリーディングで、ほんとは「2kの補数」です。8ビット整数なら、28の補数、つまり「256の補数」を使うことになります。例えば、-10 を表すのに、256に対する10の補数「256 - 10 = 246」と同じビット列を（別な解釈で）使います。解釈が変わるところが要点です。

ついでに「1の補数」というのもワカラン言葉ですが、各ビットごとのビット反転をそんな言い方をしているのです。「0→1, 1→0」が、1に対して補数取ってるよね、というだけ。

補足2： どんな仕掛けか

幅がkビットのビット列の足し算を行っているハードウェア*1は、加法群 Z/2kZ の実装になっています。Z/2kZ は、「2kで割った余りが同じ」という同値関係による商集合（の加法構造）です。

ビット列の集合 {0, 1}k （二値集合のk個のコピー達の直積）と Z/2kZ の1：1対応があって、足し算 (Z/2kZ)×(Z/2kZ)→Z/2kZ は、{0, 1}k×{0, 1}k→{0, 1}k と同一視できます。加法逆元を求める写像 {0, 1}k→{0, 1}k （「ビットを反転して1を足す」）もハードウェアに組み込みと考えます。

{0, 1}kと通常の整数Zとの対応をどう取るかは、プログラミング言語のモデルとか人間の解釈の問題です。{0, 1, 2, ..., 2k-1} ⊆ Z と {0, 1}k の対応を考えるのが符号なし整数解釈（本文では正整数解釈）、{-2k-1, ..., -1, 0, 1, ..., 2-1k-1} ⊆ Z との対応を考えるのが符号付き整数解釈（本文では正負整数解釈）となります。

「2の補数」の背後には、ビット列や文字列のような記号表現、概念的・数学的な整数の部分集合（解釈として有効な数の範囲）、加算ハードウェア（有限加法群の実装）の三者の関係があったわけです。その概要は次の図のようなものです。2kのkを例えば8にすると8ビットデータの話になります。2kの代わりに103を使ったのがこの記事の説明でした。

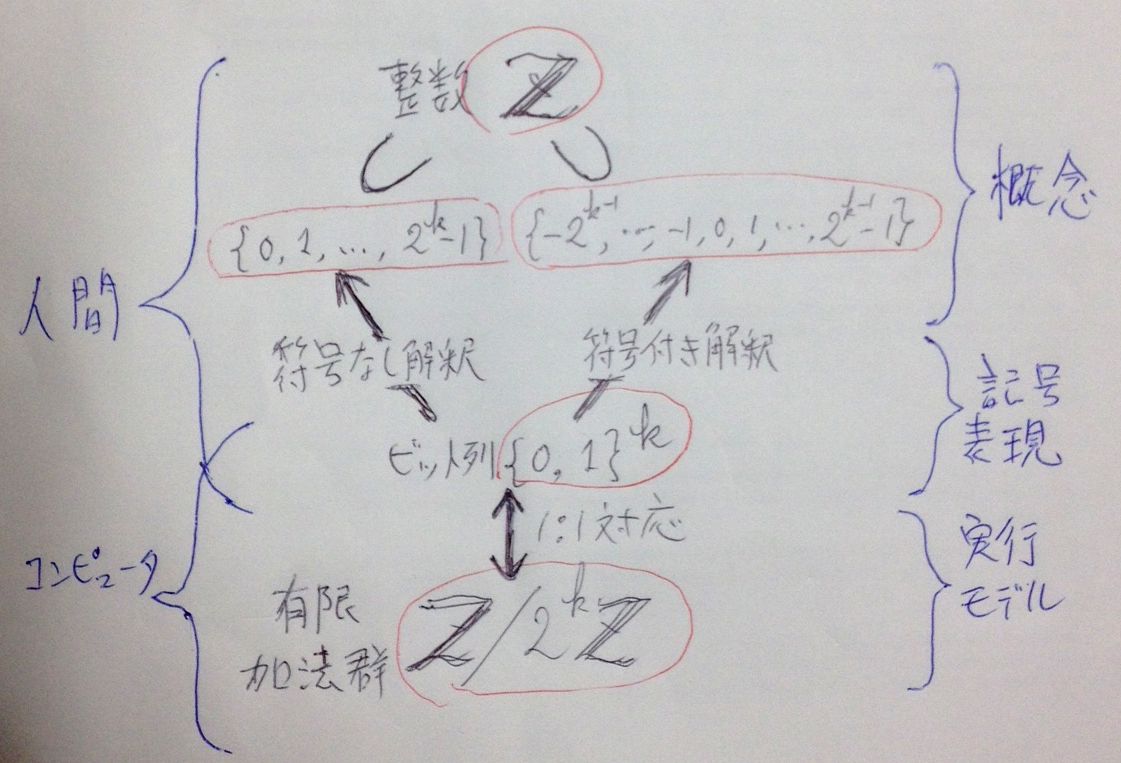
*1:今どきは、どこまでがハードウェアか分からないので、「ハードウェアに近い、ひょっとしてソフトウェアかも知れない仕掛け」くらいの意味です