このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

反転可能マルコフ圏は条件化可能

雑記／備忘

\newcommand{\cat}[1]{\mathcal{#1}} \newcommand{\In}{\text{ in } } \newcommand{\id}{\mathrm{id} } \require{color} \newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }% \newcommand{\For}{\Keyword{For } }% \newcommand{\Define}{\Keyword{Define } }% \newcommand{\Declare}{\Keyword{Declare } }% \newcommand{\Where}{\Keyword{Where } }% 表題の事実は、長／ジェイコブスの以下の論文の p.11 Proposition 3.10 として記述されています。

  • Title: Disintegration and Bayesian Inversion via String Diagrams
  • Authors: Kenta Cho, Bart Jacobs
  • Submitted: 29 Aug 2017 (v1), 8 Feb 2019 (v3)
  • Pages: 39p
  • URL: https://arxiv.org/abs/1709.00322

が、毎度「どうやるんだっけ？ ウーン、ワカラン」となるので絵を載せておきます。

\cat{C} をマルコフ圏として、次の射（同時分布）を考えます。

\quad p:{\bf 1} \to X\otimes Y \In \cat{C}

\cat{C} は反転可能、つまり任意の射と分布（域が {\bf 1} である射）に対してベイズ反転が存在するとします。射 g は次のように定義します。右肩のダガーマークがベイズ反転を意味します。

\Declare g:X \to X\otimes Y \In \cat{C}\\ \Define g := (\pi^1_{X,Y})^{\dagger p}\\ \Where\\ \quad \pi^1_{X,Y} := \id_X \otimes !_Y

g は第一射影 \pi^1_{X,Y} のベイズ反転ということです。

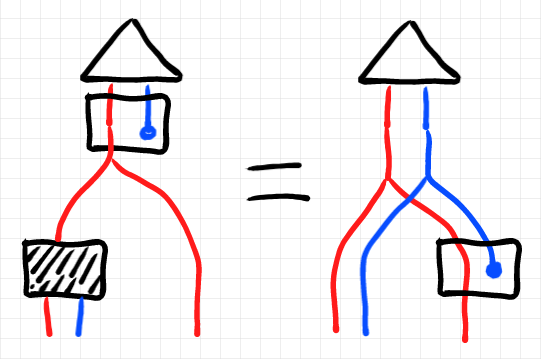
絵を描くときの約束は：

  • X ： 赤いワイヤー
  • Y ： 青いワイヤー
  • p ： 三角
  • g ： 斜線網掛けの四角

ベイズ反転の公理的な特徴付けから次が成立します。

射 f は次のように定義します。

\Declare f:X \to Y \In \cat{C}\\ \Define f := g; \pi^2_{X, Y} = (\pi^1_{X,Y})^{\dagger p}; \pi^2_{X, Y}

この f が、最初に与えられた同時分布 p の条件化になっていることを示します。そのためには、次の等式を示せばOKです。

\quad p_{!1};\Delta_X ( \id_X \otimes f) = p\\ \Where\\ \quad p_{!1} := p;\pi^1_{X, Y} = p;(\id_X \otimes !_Y)

絵算で示しましょう。

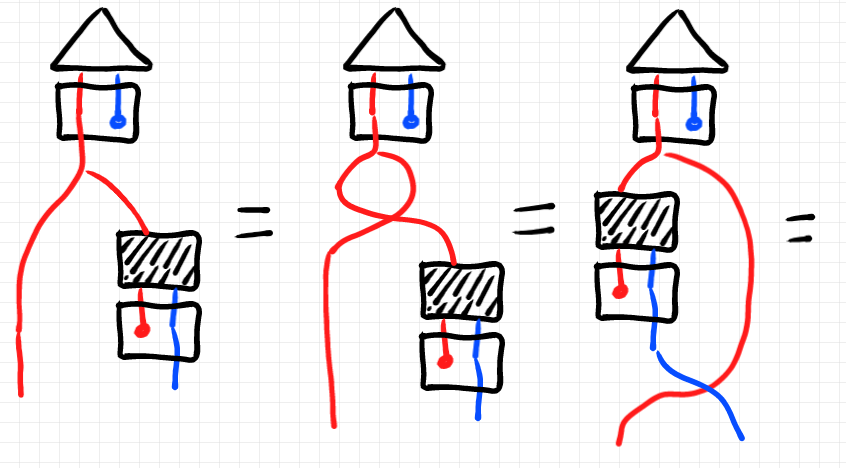
左から右に見ていくことにして； 1番目から2番目は、対角射 \Delta の余可換律です。2番目から三番目はスワップ〈対称〉に沿って射 f をスライドさせています。

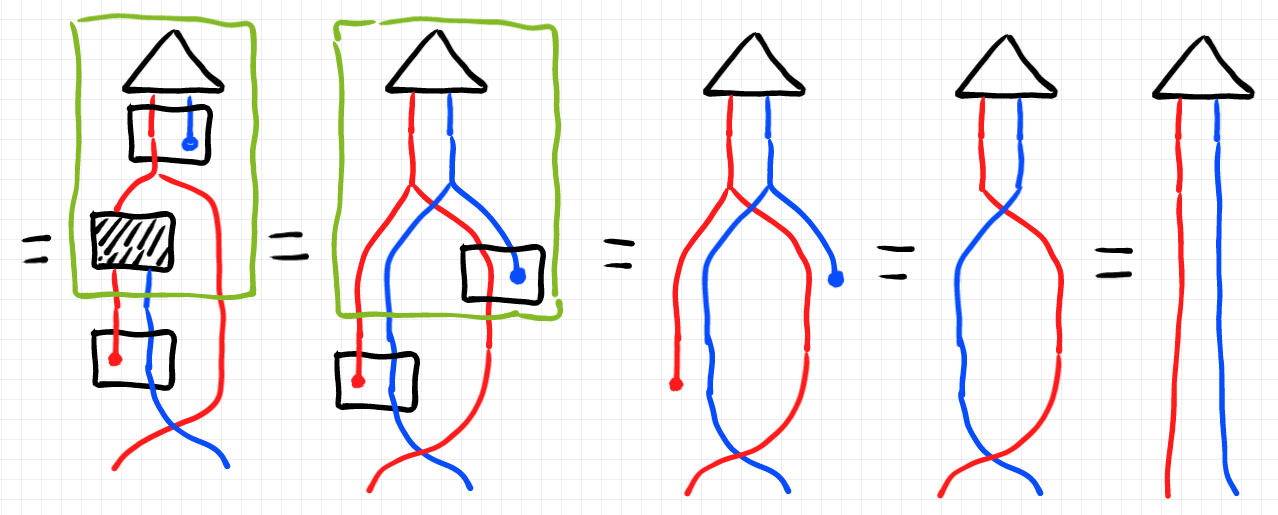
1番目から2番目は、g が第一射影のベイズ反転であることを使って変形（黄緑の枠内）しています。2番目から3番目は特に何もしてません（絵を整理しただけ）。

3番目から4番目は、対角射の余単位律です。最後はスワップを二度行うと何もしない、ということです。

以上で目的の等式

\quad p_{!1};\Delta_X ( \id_X \otimes f) = p

が示せました。f が p の条件化になっています。つまり、反転可能マルコフ圏は条件化可能であることが分かりました。