マルコフ圏におけるベイズの反転定理 - 檜山正幸のキマイラ飼育記 (はてなBlog)

ベイズの定理とかベイズの公式が何を指すかはいまいちハッキリしませんが、「マルコフ圏、ベイズの定理、陰関数定理」の最初の節で引用した定理のことだと言って間違いにはならないでしょう。フリッツ〈Tobias Fritz〉の"A synthetic approach to Markov kernels, conditional independence and theorems on sufficient statistics"にあるストリング図を拝借してその定理（あるいは公理）を述べれば：

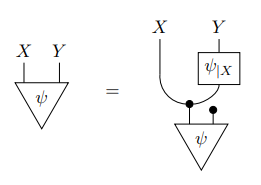
イコールの左辺にある射 $\psi : I \to X \otimes Y$ が与えられたとき、イコールの右辺にある射 $\psi_{|X}:X \to Y$ が存在することを主張します（一意的とは言ってない）。

ストリング図を使って述べているので、ストリング図が読めないと命題の意味が分かりませんが、ストリング図の原則は：

圏の対象をワイヤー〈ストリング | 線〉で描く。
単位対象は不可視のワイヤー（何も描かない）とする。
圏の射を、丸、四角、三角などのノードで描く。
上の図では、射の方向は下から上（人により描画方向はバラバラ）。

これだけです。事例、練習問題としては、例えば「図式思考の例として、コモノイドについて考えてみる」参照。

今（ストリング図を使って）述べた命題は、ベイズの条件化定理（または公理）と呼ぶことにします。条件化定理があれば、ベイズの反転定理が出ます。この記事では、条件化定理と反転定理の関係を話題にします。

内容：

象形記号
条件化可能マルコフ圏
条件化コンビネータ
周辺化コンビネータ
ベイズ反転
それから

象形記号

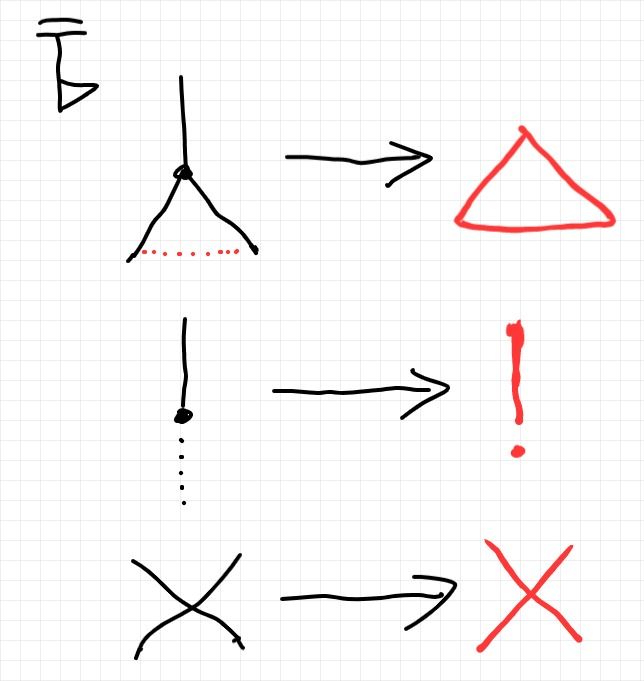
この機会に、マルコフ圏における（マルコフ圏以外でも使えるが）“象形文字的な記号”を紹介しておきます。

マルコフ圏〈Markov category〉は、対角射〈diagonal morphism〉と終射〈{terminal | final} morphism〉を持ちます。対象Aの対角射は $\Delta_A : A \to A\otimes A$ 、対象Aの終射は $!_A:A \to I$ と書きます。終射は、終対象（兼モノイド単位）への唯一の射です。対角射をコピー射〈copy morphism〉、終射を削除射〈delete morphism〉とも呼びます*1。

また、マルコフ圏は対称モノイド圏なので、対象AとBの対称射〈{symmetry | swap | flip} morphism〉 $\sigma_{A,B}:A\otimes B \to B\otimes A$ を持ちます。対称射は、 $\mathrm{X}_{A, B}$ と書くこともあります。

いま出てきた $\Delta,\; !,\; \mathrm{X}$ は、絵と形状が似た文字・記号を選んだものです*2。

図の左上の“旗”については：

絵算の描画方向を示すために旗を使うことにした

余マルコフ圏では、対角射、終射、対称射の双対である余対角射〈codiagonal morphism〉、始射〈initial morphism | 余終射 |{coterminal | cofinal} morphism〉、対称射（これは自己双対）がありますが、それらは $\nabla,\; i,\; \mathrm{X}$ と書きます。上下を逆さまにした形です。逆感嘆符 ¡ が使えるなら、ラテン文字 $i$ の代わりに使います。

ここで重大な注意です。象形記号は、射の結合方向が上から下、モノイド積の方向が左から右の描画法に基づいています。しかし、最近の多数派は「射の結合方向が下から上、モノイド積の方向が左から右」です（フリッツもこの描画方向を使っています）。適宜、描画方向を頭のなかで変換する必要があります。

条件化可能マルコフ圏

C = (C, $\otimes$ , I, α, λ, ρ, σ, Δ, !) をマルコフ圏として、公理的な議論をします。つまり、「圏論的確率論におけるCタイプとAタイプ」の言い方だと「Aタイプの圏論的確率論」をやります。念の為、マルコフ圏の構成素の意味を確認しておきます。

C は台圏〈underlying category〉
(- $\otimes$ -):C×C → C はモノイド積
I∈|C| はモノイド単位（兼終対象）
For A,B,C∈|C|, α_A,B,C:(A $\otimes$ B) $\otimes$ C → A $\otimes$ (B $\otimes$ C) は結合律子〈associator〉
For A∈|C|, λ_A:I $\otimes$ A → A は左単位律子〈left unitor〉
For A∈|C|, ρ_A:A $\otimes$ I → A は右単位律子〈right unitor〉
For A,B∈|C|, σ_A,B:A $\otimes$ B → B $\otimes$ A は対称〈symmetry〉
For A∈|C|, Δ_A:A → A $\otimes$ A は対角射
For A∈|C|, !_A:A → I は終射

これらの構成素は、対称モノイド圏の公理と、余可換コモノイド・モダリティ〈余可換コモノイド装備〉の公理を満たします。また、対称モノイド構造は半デカルト性を持ちます*4。抽象的/公理的に定義されたマルコフ圏の実例としては、マルコフ核の圏があります、「マルコフ核：確率計算のモダンな体系」参照。

ここでは、マルコフ圏Cの射は、一般に F, G などの大文字で表しますが、域がI（単位対象兼終対象）である射は s, t などの小文字で表すことにします。Cの射を表す矢印は通常の矢印を使い、'→*' のような変わった矢印は使いません。

ベイスの条件化定理（または公理）〈Bayes' conditionalization {theorem | axiom}〉を表現する命題をCONDITと置きましょう。マルコフ圏Cにおける命題CONDITは次のように定義されます。
$\mathrm{CONDIT} :\Leftrightarrow \\ \:\:\forall (s:I \to X\otimes Y \mbox{ in }\mathcal{C}). \\ \:\:\exists (F:X \to Y \mbox{ in }\mathcal{C}). \\ \:\:\:\: s = s;(\Delta_X \,\otimes\, !_Y);(\mathrm{id}_X \otimes F)$

この命題に出現する等式を表すストリング図は、先に引用したフリッツの絵です。ただし、使っている記号は違います。s と ψ 、F と ψ_|X が対応します。

命題CONDITを満たすマルコフ圏を、条件化可能マルコフ圏〈conditionalizable Markov category〉と呼ぶことにします（フリッツは Markov category with conditional distributions と呼んでいます）。

条件化コンビネータ

Cが条件化可能マルコフ圏とすると、s:I → X $\otimes$ Y in C に対して、命題CONDIT（の成立）により存在が保証される F:X → Y in C を選ぶことができます。存在の一意性は言ってないので、一意にFが決まるとは限りませんが、何かひとつ選ぶことはできます*5。

(s:I → X $\otimes$ Y) $\mapsto$ (F:X → Y) という対応を、Condit_X,Y とします。

For X,Y∈|C|, Condit_X,Y:C(I, X $\otimes$ Y) → C(X, Y) in Set

Conditは、Cの対象2つでインデックスされた写像（集合圏の射）の族になります。対象でインデックスされた射の族を、オペレータとかコンビネータと呼ぶのでした（「圏論的コンストラクタと圏論的オペレータ：関手性・自然性の呪縛からの脱却」参照）。よって、Conditは条件化コンビネータ〈{conditionalize | conditionalization} combinator〉と呼ぶのが自然でしょう。

条件化可能マルコフ圏の定義は、条件化コンビネータを使ってもできます。つまり、マルコフ圏Cとその上のコンビネータConditの組 (C, Condit) として条件化可能マルコフ圏を定義するのです。Conditが満たすべき公理は：

X,Y∈|C| に対して、Condit_X,Y は、C(I, X $\otimes$ Y) → C(X, Y) という写像である。
F = Condit_X,Y(s) とすると、s, F は、命題CONDITに登場する等式を満たす。

Condit_X,Y(s) を短く略記したいときは、s_Y|X と書くことにします（フリッツは s_|X としてますが、Yの情報が欠けています）。条件化コンビネータConditによる値 s_Y|X を、sの条件化射〈conditional morphism〉、または単に条件化〈conditional（名詞）〉と呼びます。

言葉の整理をしておきます。

	形容詞兼名詞	動詞	動詞からの名詞	可能の形容詞
英語	conditional	conditionalize	conditionalization	conditionalizable
日本語	条件{化}?	条件化する	条件化	条件化可能

周辺化コンビネータ

先に進む前に寄り道をして、周辺化コンビネータを定義しておきます。寄り道する理由は、コンビネータ〈オペレータ〉を積極的に使ってほしいからです。何かを圏論的に定式化するとき、圏を定義するだけではなくて、圏上のコンビネータ／オペレータも一緒に考えることが多いのです。コンビネータ／オペレータの計算が主題となるときもあります。

周辺化〈marginalize〉は、次の形のコンビネータとなります。

For A,X,Y∈|C|, Marg_{A,(X, Y)}¹:C(A, X $\otimes$ Y) → C(A, X)
For A,X,Y∈|C|, Marg_{A,(X, Y)}²:C(A, X $\otimes$ Y) → C(A, Y)

周辺化の定義は簡単で：

For F∈C(A, X $\otimes$ Y), Marg_{A,(X, Y)}¹(F) := F;(id_X $\otimes$ !_Y);ρ_X
For F∈C(A, X $\otimes$ Y), Marg_{A,(X, Y)}²(f) := F;(!_X $\otimes$ id_Y);λ_Y

特に、A = I のときは次のように略記します。

Marg_X,Y¹ := Marg_A,(X,Y)¹
Marg_X,Y² := Marg_A,(X,Y)²

さらに、s_X := Marg_X,Y¹(s), s_Y := Marg_X,Y²(s) のような短縮記法も使いますが、略記に略記を重ねると意味不明になるので、Marg¹(s), Marg²(s) くらいに留めたほうがいいと思います。

ここでも言葉の整理をしておきます。

	形容詞兼名詞	動詞	動詞からの名詞	可能の形容詞
英語	marginal	marginalize	marginalization	marginalizable
日本語	周辺{化}?	周辺化する	周辺化	周辺化可能

ベイズ反転

マルコフ圏の枠組みでは、ベイズ反転とは、ある射 F:X → Y in C に対して、方向が逆の射 G:Y → X in C を対応させるコンビネータです。もちろん、コンビネータの性質を規定する公理が付きます。

今ここでは、ベイズ反転コンビネータを公理的に定義するのではなく、マルコフ圏が条件化可能（条件化コンビネータを持つ）と仮定して、条件化コンビネータからベイズ反転コンビネータを作り出す〈構成する〉アプローチを取ります。このとき、最初に与えられる（反転する前の）射を確率モデル〈統計モデル〉と考えると分かりやすいので、そういうセッティングで話をします。

ベイズ反転は、通常 Bayesian inversion と呼びますが、ドバーカット〈Ernst-Erich Doberkat〉などが指摘しているように「逆射じゃないのに逆と呼ぶのはおかしい」ので、Bayesian conversion と呼び、コンビネータ名はConvsとします。

さて、条件化可能マルコフ圏C内のパラメトリック確率モデル〈parametric probabilistic model〉とは、Cの射のことです。「えっ？」と思うかも知れませんが、単なる射です。気分の問題として、射をパラメトリック確率モデルとみなすときは M:Θ → X in C と書きましょう。Mの域Θをパラメータ空間〈parameter space〉、余域Xを値空間〈value space〉またはデータ空間〈data space〉と呼びます。繰り返しますが、形式的には、パラメトリック確率モデル＝射です。

パラメトリック確率モデル（以下、単に「確率モデル」ともいう）M:Θ → X in C だけでは反転することができません。パラメータ空間Θ上に“事前分布”を与えます。s:I → Θ in C を事前分布とします。事前分布sによるMの反転（これから定義する）は、Convs_Θ,X(M, s) と書きます。Convsは次のようなコンビネータになります。

For Θ,X∈|C|, Convs_Θ,X:C(Θ, X)×C(I, Θ) → C(X, Θ)

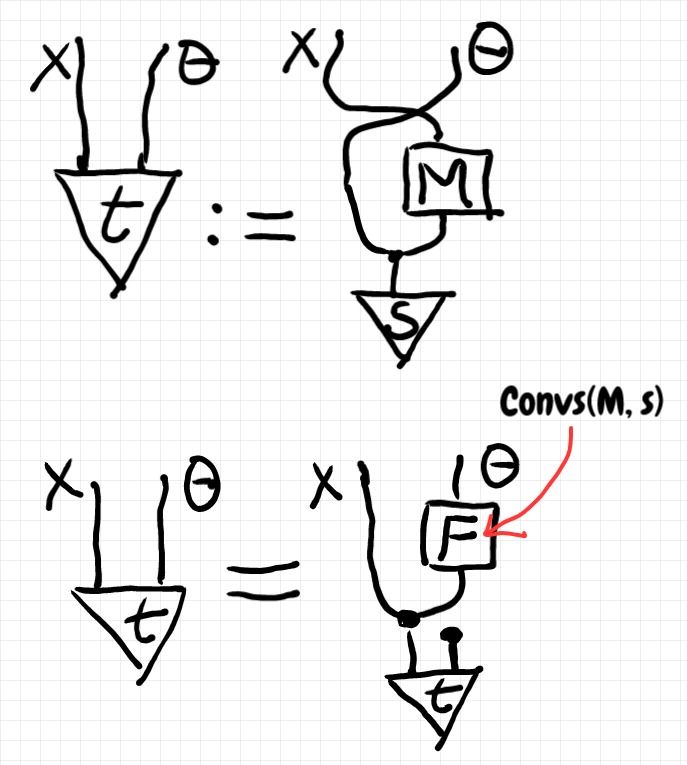
M∈C(Θ, X) と s∈C(I, Θ) から Convs_Θ,X(M, s) を作る手順は二段階に分けるのがいいでしょう。

t:I → X $\otimes$ Θ を t := s;Δ_Θ;(id_Θ $\otimes$ M);σ_Θ,X と定義する。
F := Condit_X,Θ(t) とする。このFが Convs_Θ,X(M, s) 。

まとめて書けば：

Convs_Θ,X(M, s) := Condit_X,Θ(s;Δ_Θ;(id_Θ $\otimes$ M);σ_Θ,X)

これが、Mのsによるベイズ反転〈Bayesian conversion〉です。

二段階に分けた手順を絵で描けば（射の描画方向は下から上）：

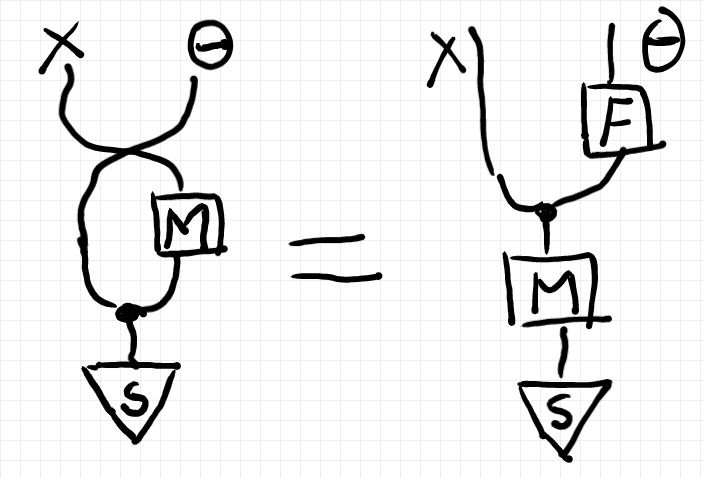
少し計算（絵算）すると、s, M, F のあいだに次の等式が成立することが分かります。

テキスト数式で書けば：

$s;\Delta_\Theta;(\mathrm{id}_\Theta \otimes M);\sigma_{\Theta,X} = s;M;\Delta_X;(\mathrm{id}_X \otimes F)$

この等式は、ベイズ反転を公理的に定義するときの条件式になります。つまり、与えられたMとsに対して、この等式を満たすようなFが（あれば、それが） Convs(M, s) です。

有限離散の具体的な場合 Θ = {1, 2, ..., n}, X = {1, 2, ...,m} を考えると、F = Convs(M, s) は次の公式で計算できます。

$\mbox{For }i\in \Theta, j\in X, \: F(j)(\{i\}) = \frac{s(\{i\})M(i)(\{j\})} {\sum_{k\in \Theta}s(\{k\})M(k)(\{j\})}$

得られた F = Convs(M, s) は、確率モデルMに対する、事前分布sを仮定したときのベイズ推測射〈Bayesian inference morphism〉*8です。上の具体的な場合で言えば、F(j)は、値〈データ〉jが観測されたときのパラメータiの分布です。観測値jは確定値ですが、パラメータの推測値は不確定値、つまり分布です。それにそもそも、仮定した事前分布 s:I → Θ に根拠はないかも知れません。

さて、また言葉の整理をしておきます。

	形容詞兼名詞	動詞	動詞からの名詞	可能の形容詞
英語	converse	converse	conversion	convertible
日本語	反転	反転する	反転	反転可能

それから

マルコフ圏Cは対称モノイド圏です。「簡約多圏とシーケント計算」で述べた方法により簡約多圏 PermStdPoly(C) が作れます。C で議論するよりは、PermStdPoly(C) で議論したほうがより現実的・実践的です。PermStdPoly(C) のほうが具体的な計算には有利・便利なのです。

「ベイズ反転は、ほんとの逆射ではないから inversion と呼ぶのは不適切」という意見はもっともですが、適当なセッティングのもとでは、ベイズ反転を逆射と考えることが出来る気がします。今のところ確証はないですが、状況証拠は幾つかあります。「ほんとの逆射」まではいかないかも知れませんが、逆射扱いしていい状況がありそう。もし、ベイズ反転を逆射扱いしていいなら、計算はだいぶ気楽になります。ちょっと考えてみますわ。

*1:終射は、discharger, discarder などとも呼びます。

*2:Δは、diagonal の'd'にも由来するかも知れません。

*3:Web上の画像： https://sketch.io/render/sk-3ebc51e5cb7224010942fe4e639d8c39.jpeg

*4:半デカルト性は邪魔なこともあります。「マルコフ圏の一族 // 準マルコフ圏」参照。

*5:コンビネータConditは、存在命題としてのCONDITのスコーレム化〈Skolemization〉と言えます。

*6:Web上の画像： https://sketch.io/render/sk-9456ff356e8be587af8d74039df3ce47.jpeg

*7:Web上の画像： https://sketch.io/render/sk-68427cf1f534d80190046d394b5a735d.jpeg

*8:この場合の inference は、「推論」「推測」「推定」のどれがいいのでしょうか？