昨日の記事「大域米田の補題」において、大域米田の補題に関する計算について、次のように書きました。
テキストで計算していると何がなんだかワケワカメになることがあるので、絵算〈{pictorial | graphical} calculus〉を利用するのが得策でしょう。「米田の補題とストリング図」で述べた手法が使えます。
このテの計算に絵算は使えるし、実際に僕は絵算を使っています。テキストで記述・計算するより、ずっと見通しがいいと思います。
が、ややこしい問題もあります。ストリング図のワイヤーに向きを付けるとき、どんな約束にするか? -- これ、ややこしい。通常は、キャンバスの描画方向を決めておくだけでいいのですが、反対圏/反変関手が出てくると、状況は単純ではなくなります。$`\newcommand{\cat}[1]{\mathcal{#1}}
%\newcommand{\Imp}{ \Rightarrow }
\newcommand{\For}{\text{For }}
\newcommand{\In}{ \text{ in } }
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\hyp}{\text{-}}
%\newcommand{\Iff}{\Leftrightarrow}
\newcommand{\whitestar}{\unicode{x2606} }
\newcommand{\op}{\mathrm{op}}
`$
内容:
反対圏
圏は、対象の集合、射の集合、それと写像達 $`\mrm{dom},\mrm{cod},\mrm{id},\mrm{comp}`$(域、余域、恒等、結合)で定義されます。圏 $`\cat{C}`$ の対象の集合、射の集合を $`\mrm{Obj}(\cat{C}), \mrm{Mor}(\cat{C})`$ として、圏 $`\cat{C}`$ の構造を与える写像達には、左肩添字として $`\cat{C}`$ を添えることにします。例えば $`{^\cat{C}\mrm{dom}}`$ のように。
圏 $`\cat{C}`$ があるとき、その反対圏 $`\cat{C}^\op`$ は次のように定義されます。$`\mrm{swap}`$ はペアの順番(あるいは左右)を入れ替える写像です。
- $`\mrm{Obj}(\cat{C}^\op) := \mrm{Obj}(\cat{C})`$
- $`\mrm{Mor}(\cat{C}^\op) := \mrm{Mor}(\cat{C})`$
- $`{^{\cat{C}^\op} \mrm{dom}} := {^{\cat{C}} \mrm{cod}}`$
- $`{^{\cat{C}^\op} \mrm{cod}} := {^{\cat{C}} \mrm{dom}}`$
- $`{^{\cat{C}^\op} \mrm{id}} := {^{\cat{C}} \mrm{id}}`$
- $`{^{\cat{C}^\op} \mrm{comp}} := \mrm{swap};{^{\cat{C}} \mrm{comp}} = {^{\cat{C}} \mrm{comp}} \circ \mrm{swap}`$
これが、反対圏の定義のすべてです。$`\cat{C}`$ が圏ならば、新しく作った構造 $`\cat{C}^\op`$ も間違いなく圏になります。したがって、$`\cat{C}^\op`$ は圏です。
これ以上の意味は何もありません。ほんとに何もないんです。余計なことを考える必要はありません。余計なことを考えてはダメです。
例えば、集合圏 $`{\bf Set}`$ の反対圏 $`{\bf Set}`$ は上記の定義に従って確実に作れます。それに対して、「出力が先に与えられたら、入力は一意に決まらないからダメじゃん」とか「関数アルゴリズムの逆、つまり時間を逆行させるのか」とか、そんなん余計なことです。そういう無理やりな意味付けをする前に、上記のドライな定義を受け入れて下さい。
とはいえ、ある圏 $`\cat{C}`$ の反対圏 $`\cat{C}^\op`$ と圏同型または圏同値になる圏 $`\cat{D}`$ を探す/構成するのはとても重要な問題です。これが重要な問題だと理解するためにも、いったんはドライな定義で反対圏を了解する必要があります。
反変関手
$`F:\cat{C} \to \cat{D}`$ が反変関手だとは、通常の関手〈共変関手〉とほとんど同じですが、次の条件を満たすときです。
$`\For f:A\to B, g:B \to C \In \cat{C}\\
\quad F(f;g) = F(g);F(f) \In \cat{D}
`$
共変関手と反変関手は違う条件で定義されるので違うものです。区別が付くように書いたほうがいいでしょう。例えば、矢印にプラス・マイナスの符号を付けるとか。
$`\quad F:\cat{C} \overset{+}{\to} \cat{D} \:\text{ 共変関手}\\
\quad G:\cat{C} \overset{-}{\to} \cat{D} \:\text{ 反変関手}
`$
関手の結合〈composition〉に関して、掛け算の符号と同じルールになります。
- 共変関手(プラス)と共変関手(プラス)の結合は共変関手(プラス)
- 共変関手(プラス)と反変関手(マイナス)の結合は反変関手(マイナス)
- 反変関手(マイナス)と共変関手(プラス)の結合は反変関手(マイナス)
- 反変関手(マイナス)と反変関手(マイナス)の結合は共変関手(プラス)
しかし実際には、プラス・マイナスの符号もその他の目印も(ほとんど)使われていません。現在の主流は、共変関手だけを考えて、反変関手は使わない方式です。
「反変関手も必要だろう」 -- そのとおり、必要です。反変関手 $`F:\cat{C} \overset{-}{\to} \cat{D}`$ の代わりに、反対圏からの関手を使います。そして、代理である反対圏からの関手を「反変関手」と呼んでしまうのです。
$`\quad F:\cat{C}^\op \to \cat{D} \In {\bf CAT}`$
つまり、“圏の2-圏” $`{\bf CAT}`$ の対象類 $`|{\bf CAT}|`$ 上に、反対圏を対応させる対合〈involution〉を考えれば済むということです。
$`\quad (\hyp)^\op : |{\bf CAT}| \to |{\bf CAT}| \In \mathbb{SET}`$
代理ではなくて本来の反変関手を考えたいなら、共変関手しか持たない“圏の2-圏” $`{\bf CAT}`$ ではなくて、ほんとの反変関手も含む“圏の2-圏” $`{\overline{\bf CAT}}`$ を考える必要があります。$`{\overline{\bf CAT}}`$ のなかでは、前述のプラス・マイナス符号のような目印が必要です(それが面倒だから代理を使っているわけですが)。
$`{\overline{\bf CAT}}`$ の共変関手だけを考えて部分2-圏 $`{\overline{\bf CAT}}^+`$ を作れます。$`{\bf CAT}`$ は$`{\overline{\bf CAT}}`$のなかに標準的に埋め込めて、その像が $`{\overline{\bf CAT}}^+`$ になります。$`{\bf CAT}`$ と $`{\overline{\bf CAT}}^+`$ は同一視してかまいません。
$`{\overline{\bf CAT}}`$ の代わりに $`{\bf CAT}`$ を使うには、ほんとの反変関手達を $`{\bf CAT}`$ のなかに押し込めてしまう必要があります。押し込め〈レトラクション〉に使われるのが次の対応です(「層化ストリング図 // 裏返し反変関手」を参照)。
$`\quad (F: \cat{C} \overset{-}{\to} \cat{D}) \mapsto ({^\mrm{rev} F} : \cat{C}^\op \to \cat{D})\\
\quad (F: \cat{C} \overset{-}{\to} \cat{D}) \mapsto ( F^{\mrm{rev}} : \cat{C} \to \cat{D}^\op)
`$
扱いに困るのは $`{^\mrm{rev} F^{\mrm{rev}}}`$ です。内容的には $`F`$ とまったく同じですが、関手の域と余域は違うと言えば違うのです。「大域米田の補題」では、臨時に $`\widetilde{F}`$ という書き方をしてました。
実際のところは、「ほとんど $`{\bf CAT}`$ と反対圏で済ませられるが、稀に $`{\overline{\bf CAT}}`$ を考える必要が生じる」ということですね。
2-圏のストリング図とレーン
ここで考える2-圏は、小さくない圏も含む“圏の2-圏”である $`{\bf CAT}`$ です。一般論として通用する議論もありますが、もっぱら $`{\bf CAT}`$ を扱います。
「反対圏」「反変関手」で述べた事情は、$`{\bf CAT}`$ のストリング図を描くときも影響を与えます。ワイヤーに向きのマーカーをどう付けるか? という問題があります。
まず、2-圏 $`{\bf CAT}`$ におけるストリング図のセル〈描画・視覚化の基本要素〉を確認しておきます。次元はポアンカレ双対で逆転します。
| 圏〈0-射〉 | 2次元エリア |
| 関手〈1-射〉 | 1次元ワイヤー |
| 自然変換〈2-射〉 | 0次元ノード |
キャンバスは2次元で、描画方向は、自然変換の縦結合が上から下、関手の結合/自然変換の横結合が左から右と決めます。この描画方向は、この記事内では決め打ちで変更しません。
2つの圏($`{\bf CAT}`$ の対象) $`\cat{C}, \cat{D}`$ を固定して、これを左右のエリアとして描くとすると、中央縦方向に関手圏(あるいはホム圏)$`[\cat{C}, \cat{D}]`$ の対象(関手/ワイヤー)と射(自然変換/ノード)を描くことになります。関手圏の対象/射を描くために予約された縦方向の帯状の領域をレーン〈lane〉と呼ぶことにします。
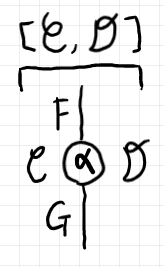
レーンは、関手ボックスやストライプとは違い、特に実体はなくて単にキャンバスの一部を意味するだけです。
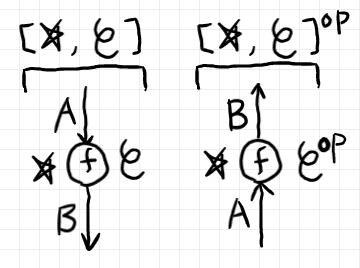
$`[\cat{C}, \cat{D}]`$ とマークされたレーン内のワイヤーには、上から下(順方向)への矢印で方向付けします。一方、$`[\cat{C}, \cat{D}]^\op`$ とマークされたレーン内のワイヤーには、下から上(逆方向)への矢印で方向付けします。これは、キャンバスの描画方向を変更するものではありません。
ワイヤーの方向は、常に上から下へと読みます(キャンバスのルール)。逆方向の矢印は次の意味です。
- そのワイヤーが反対圏の射を表すことを明示する。
- 反対圏のもとの圏($`{^\op}`$ が付かない圏)の射は、実際に反対向きである。
繰り返し注意しますが:
- 矢印は単なる注釈情報であって、関手圏の1-射(圏の2-圏の2-射)の方向は上から下である。
特別な圏と関手圏
次の圏は、$`{\bf CAT}`$ の対象のなかでも特別なものです。
- $`\whitestar`$ : 単一の対象と恒等射だけを持つ自明圏
- $`{\bf Set}`$ : 集合圏(対象は小さい集合)
任意の圏 $`\cat{C} \in |{\bf CAT}|`$ に対して次の圏同型(圏同値より強い)が成立します。
- $`[\whitestar, \cat{C}] \cong \cat{C}`$
- $`[\whitestar, \cat{C}]^\op \cong [\whitestar, \cat{C}^\op] \cong \cat{C}^\op`$
この圏同型によって:
- $`[\whitestar, \cat{C}]`$ の対象/射を $`\cat{C}`$ の対象/射と同一視する。
- $`[\whitestar, \cat{C}]^\op`$ の対象/射を $`\cat{C}^\op`$ の対象/射と同一視する。
圏同型に基づく同一視は、ストリング図では次のように解釈されます。
- $`[\whitestar, \cat{C}]`$ とマークされたレーン内の対象(ワイヤー)と射(ノード)は、$`\cat{C}`$ の対象/射であるかのようにみなす。
- $`[\whitestar, \cat{C}]^\op`$ とマークされたレーン内の対象(ワイヤー)と射(ノード)は、$`\cat{C}^\op`$ の対象/射であるかのようにみなす。
反対圏のレーンでは、逆向きの矢印を付けるルールも採用すると、次のように描画します。
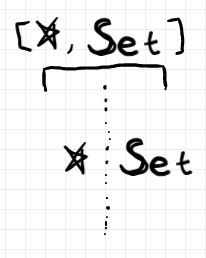
$`[\whitestar, {\bf Set}]`$ とマークされたレーンに描かれるワイヤーは集合とみなされ、ノードは写像とみなされます。特に単元集合 $`{\bf 1}\in |{\bf Set}|`$ は頻繁に使うので、点線ワイヤーで描くと決めておきます。$`{\bf 1}`$ とラベルされていなくても点線なら $`{\bf 1}`$ のことです。
集合の要素
集合の要素 $`a\in A`$ があるとき、要素はポインティング射〈ポインティング写像〉とみなせます。
$`\quad a:{\bf 1} \to A \In {\bf Set}`$
集合圏の対象・射は、自明圏からの関手・自然変換と解釈できるので、
$`\quad a:: {\bf 1} \Rightarrow A : \whitestar \to {\bf Set} \In {\bf CAT}`$
これは、自明圏からの関手圏内でも解釈できるので、
$`\quad a: {\bf 1} \to A \In [\whitestar, {\bf Set}]`$
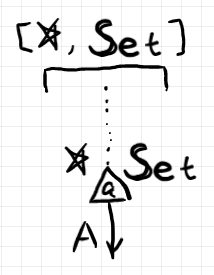
2-圏 $`{\bf CAT}`$ のストリング図では、集合の要素は、$`[\whitestar, {\bf Set}]`$ とマークされたレーン内のノードとして描画されます。要素を表すノードの上側のワイヤーは点線になります。好みの問題ではありますが、僕は、要素を表すノードを三角形にしています。
反対圏の対象と射のテキスト表示
ストリング図では、反対圏 $`\cat{C}^\op`$ の対象と射は、$`[\whitestar, \cat{C}]^\op`$ とマークされたレーン内に描かれます。したがって、下から上の逆行矢印が付きます。この逆行矢印は注釈情報です(描画方向には影響ない)。同様な注釈情報をテキストでも付けたいときがあります。
定義上は、$`\cat{C}`$ の対象・射と $`\cat{C}^\op`$ の対象・射はまったく同じです。
- $`\mrm{Obj}(\cat{C}) = \mrm{Obj}(\cat{C}^\op)`$
- $`\mrm{Mor}(\cat{C}) = \mrm{Mor}(\cat{C}^\op)`$
したがって、$`A\in |\cat{C}|`$ なら $`A\in |\cat{C}^\op|`$ です。しかし、注釈情報を添える意味で次の記法を使ってもいいでしょう。
- $`\cat{C}^\op`$ の対象としての $`A\in \mrm{Obj}(\cat{C}) = \mrm{Obj}(\cat{C}^\op)`$ は $`A^\uparrow`$ と書く。
- $`\cat{C}^\op`$ の射としての $`f\in \mrm{Mor}(\cat{C}) = \mrm{Mor}(\cat{C}^\op)`$ は $`f^\uparrow`$ と書く。
上向き矢印は注釈情報なので、なくてもいいし、取り去っても何も変わりません。それでも、反対圏や反変関手につきまとう混乱を避ける効果はあります。