ストリング図と相性が良いテンソル計算 2/2

「ストリング図と相性が良いテンソル計算 1/2」の続きです。今回は、ベイズ確率やデータベースで実際に使う記述・計算を紹介します。$`\newcommand{\Idx}[2]{
{\scriptsize \begin{pmatrix} #1 \\ \downarrow\\ #2\end{pmatrix} } }
%\newcommand{\IdxDU}[2]{ % index down-to-up {\scriptsize \begin{pmatrix} #2 \\ \uparrow\\ #1\end{pmatrix} } }
\newcommand{\conc}{\mathop{\#}}
\newcommand{\I}{\mathrm{I}}
\newcommand{\X}{\mathrm{X}}
\require{color}
\newcommand{\di}[1]{\textcolor{orange}{#1} } % dummy index
%\newcommand{\dii}[1]{\textcolor{skyblue}{#1} }
\newcommand{\C}{\mathop{;}} % composition
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Where}{\Keyword{Where } }%
%\newcommand{\Then}{\Keyword{Then } }%
%`$

内容：

• 関連記事群のハブ記事： ストリング図と相性が良いテンソル計算 1/2

恒等、コピー、スワップ

恒等テンソル、コピーテンソル、スワップテンソルは、象形文字で表します（「ストリング図とテンソル計算： クソバカ丁寧編 // 特別なテンソル、象形文字と成分表示」参照）。これらのテンソルのプロファイルは以下のようです。スワップの象形文字 $`\X`$ とインデックス集合 $`X`$ がフォントの違いしかなく紛らわしいので注意してください。

• $`\I_X:X \to X`$ 恒等テンソル
• $`\Delta_X:X \to X \otimes X`$ コピーテンソル
• $`\X_{X, Y}:X\otimes Y \to Y \otimes X`$ スワップテンソル

これは単純なケースのプロファイルですが、

$`\quad X = (X_1, \cdots, X_n)\\
\quad Y = (Y_1, \cdots, Y_m)\\
\quad X \otimes Y = X \conc Y = (X_1, \cdots, X_n, Y_1, \cdots, Y_m)\\
\quad x = (x_1, \cdots, x_n) \in X_1\times \cdots \times X_n\\
\quad y = (y_1, \cdots, y_m) \in Y_1\times \cdots \times Y_m
`$

のように解釈すれば一般の場合も取り込めます。

恒等テンソル、コピーテンソル、スワップテンソルの成分はクロネッカーのデルタを使って表示できます。

$`\quad \I\Idx{x}{x'} = \delta(x, x')\\
\quad \Delta\Idx{x}{x', x''} = \delta(x, x')\delta(x, x'')\\
\quad \X\Idx{x, y}{y', x'} = \delta(x, x')\delta(y, y')`$

「ストリング図とテンソル計算： クソバカ丁寧編」のような律儀・愚直な計算では、クロネッカーのデルタが大活躍しますが、今回は、クロネッカーのデルタまで落とし込んで計算することはあまりないです。

恒等テンソルの成分表示のときの注意事項を幾つか言っておきます。

恒等テンソルのインデックスは、$`\I\Idx{x}{x}`$ のように同じ文字を使いたくなりますが、これはマズイです。「同じインデックスが上下に出現していたら和を取る」というアインシュタインの総和規則が適用されてしまいます（すぐ下）。

$`\quad \I\Idx{x}{x}\\
= \I\Idx{\di{x}}{\di{x}}\\
= \sum_{x\in X}\I\Idx{x}{x}\\
= \sum_{x\in X}\delta(x, x)\\
= \sum_{x\in X} 1`$

この計算から、$`\I\Idx{\di{x}}{\di{x}}`$ の値は、集合 $`X`$ の個数〈基数〉になることが分かります。また、$`\I\Idx{\di{x}}{\di{x}}`$ を図示するときは輪を描きます。

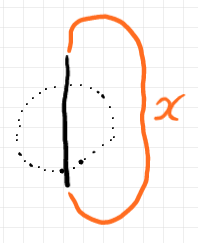
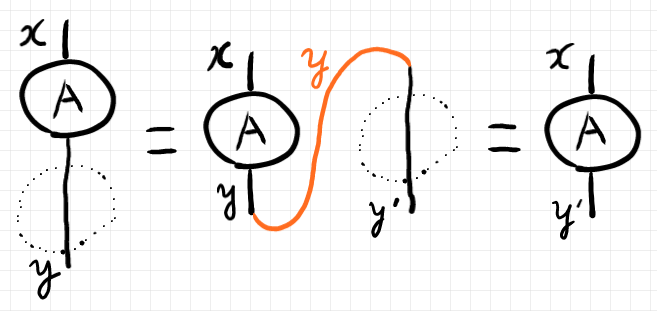
輪を作りたいとき以外は、$`\I\Idx{x}{x'}`$ のようにインデックスの名前を変えます。何らかのテンソルを恒等テンソルと結合〈composition〉しても変化しませんが、インデックスの名前はリネームされます。

$`\quad (A\C \I)\Idx{x}{y} \\
= A\Idx{x}{\di{y}}\I\Idx{\di{y}}{y'}\\
= A\Idx{x}{\di{y}}\delta(\di{y}, y')\\
= A\Idx{x}{y'}`$

対応するストリング図は以下のようです。

リネームされるメカニズムは、アインシュタインの総和規則とクロネッカーのデルタに関する公式が組み合わさっています。

$`\quad A\Idx{x}{\di{y}}\delta(\di{y}, y')\\
= \sum_{y \in Y} A\Idx{x}{y}\delta(y, y')\\
= \sum_{y \in Y} \delta_{y'}(y) A\Idx{x}{y}\\
= A\Idx{x}{y'}
`$

「関数の仮引数〈入力変数〉の名前が変わっても同じだ」ということを、ラムダ計算ではアルファ変換／アルファ同値という言葉で表現します。テンソル計算でも、「テンソルのインデックスの名前が変わっても同じだ」と言えます。だから、$`A\C \I = A`$ です。

結合に関して恒等テンソルは消えてしまいます（有っても無くても同じです）が、テンソル積に関しては消せません。

$`\quad (A\otimes \I)\Idx{x, y}{y', y''} \\
= A\Idx{x}{y} \I\Idx{y'}{y''}`$

ただし、さらに計算を続ける過程で $`\I\Idx{y'}{y''}`$ が消えることはあります（後で例が出てきます）。

コピーテンソルのインデックス操作

コピーテンソル $`\Delta_X:X \to X \otimes X`$ の成分も、異なる3つのインデックスを使って書きます。

$`\quad \Delta\Idx{x}{x', x''}`$

ベイズ確率の計算では、コピーテンソルが頻繁に出てきます。$`\Delta\C G`$ と $`F\C \Delta`$ の成分表示を見ておきましょう。

$`\quad G: X\otimes X \to Y\\
\quad F: X \to Y`$

$`\Delta\C G`$ の成分は次のように書けます。クロネッカーのデルタでインデックスがリネームされることを使っています。

$`\quad (\Delta\C G)\Idx{x}{y} \\
= \Delta\Idx{x}{\di{x'}, \di{x''}} G\Idx{\di{x'}, \di{x''}}{y}\\
= \delta(x, \di{x'}) \delta(x, \di{x''}) G\Idx{\di{x'}, \di{x''}}{y}\\
= \delta(x, \di{x'}) G\Idx{\di{x'}, x}{y}\\
= G\Idx{x, x}{y}`$

$`\Delta`$ がプレ結合〈pre-composition〉されていることは、同じインデックスが上側にニ度出現することで表現します。

$`\Delta`$ のポスト結合〈post-composition〉$`F\C \Delta`$ の場合は、単純にインデックスを重複させて $`F\Idx{x}{y, y}`$ と書けるわけではありません。そのまま書くより短く書けるように、次の記号の約束をします。

$`\Define F_\Delta := F\C \Delta`$

成分は：

$`\quad F_\Delta\Idx{x}{y', y''}`$

気分だけの問題ですが、$`F_\Delta`$ を図示するときは、ノードから直接分岐した2本のワイヤーが出ているように描きます。

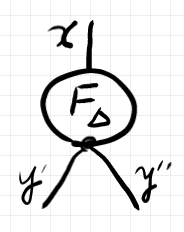
例題

次のストリング図をテキストに翻訳してみます。「ストリング図とテンソル計算： クソバカ丁寧編」のように、こまめな変換と愚直な簡約の手順を踏むのではなくて、できるだけ計算をしないで直接的にテキストに書き換えます。

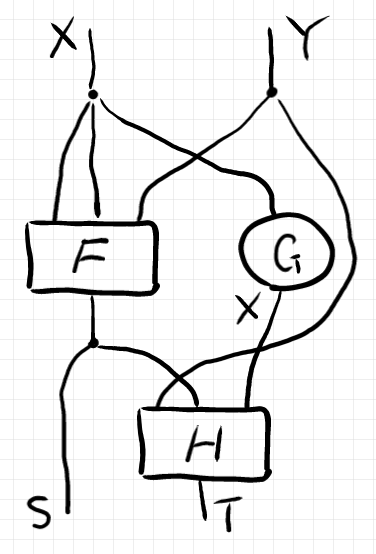
上記のストリング図を高水準のテキストで書くなら次のようになります。

$`\quad F: X\otimes X \otimes Y \to S\\
\quad G: X \to X\\
\quad H: Y\otimes S\otimes X \to T\\
\:\\
\quad (\Delta^3_X \otimes \Delta_Y) \C \\
\quad (\I_X \otimes \I_X \otimes \X_{X,Y} \otimes \I_Y ) \C \\
\quad (F \otimes G \otimes \I_Y) \C \\
\quad (\Delta_S \otimes \X_{X, Y}) \C \\
\quad (\I_S \otimes \X_{S, Y} \otimes \I_X) \C \\
\quad (\I_S \otimes H)`$

これを成分表示したらドエライことになるか？ というとそうでもありません。

ワイヤーが分岐するコピー $`\Delta`$ や $`\Delta^3`$ （三方向への分岐）は、成分表示のインデックスを重複させることで表現できます。スワップ $`\X`$ は変数の出現順で表現できます。結果的に、コピー／スワップを明示的に書く必要はなくなります。

まずは、テキストへの翻訳を、ストリング図のレイアウトに近いレイアウトで書いてみることにします。次のようになります。こう書くと、ダミーインデックスの出現位置の変更が、ワイヤーの置換を表していることが分かります。

$`
\quad \left(F_\Delta\Idx{x, x, y}{\di{s'}, \di{s''}} G\Idx{x}{\di{x'}} \I\Idx{y}{\di{y'}} \right) \\
\quad \left( \I\Idx{\di{s'}}{s} H\Idx{\di{y'}, \di{s''}, \di{x'}}{t}\right)`$

上段の $`\I`$ を省略して $`H`$ の上側インデックスに直接 $`y`$ を書いても同じです。また、下段の $`\I`$ を省略して $`F_\Delta`$ の下側インデックスに直接 $`s`$ を書いても同じです。次のように簡約できます。

$`
\quad \left(F_\Delta\Idx{x, x, y}{s, \di{s''}} G\Idx{x}{\di{x'}} \right) \\
\quad \left( H\Idx{y, \di{s''}, \di{x'}}{t}\right)`$

これを横一行にします。$`\di{s''}`$ は $`\di{s'}`$ にリネームしました。

$`\quad F_\Delta\Idx{x, x, y}{s, \di{s'}} G\Idx{x}{\di{x'}}
H\Idx{y, \di{s'}, \di{x'}}{t}`$

このテキスト表現に近いレイアウトのストリング図を描けば次のようです。

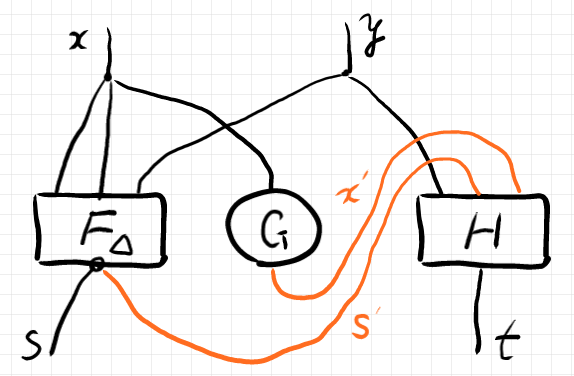
インデックスの工夫により、コンパクトなテキスト表現が得られることが分かったでしょう。

ワイヤーベンディングと転置／反転に関する注意

ここから先でも、単に $`X`$ と書いても $`(X_1, \cdots, X_n)`$ のようなリストかも知れないと解釈してください。

「ストリング図とテンソル計算： クソバカ丁寧編」で、ワイヤーベンディング・オペレーターの話をしました。例えば、オペレーター $`\mathrm{LRBend}`$（"lower right bending"）は次のように図示されます。

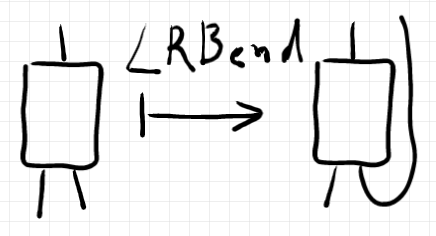
$`\mathrm{LRBend}(A) = A_{\cup}`$ のように略記します。略記は象形文字的であり便利ですが、正確な情報は伝わりません。正確には、ワイヤーベンディングに関与する3本のワイヤーの情報を記述して次のように書く必要があります。

$`\quad \mathrm{LRBend}_{X, Y, Z}(A): X\otimes Z \to Y`$

$`X, Y, Z`$ が集合のリストである場合、その旨まで明示すれば：

$`\quad \mathrm{LRBend}_{(X_1, \cdots, X_n), (Y_1, \cdots, Y_m), (Z_1, \cdots, Z_l)}(A): (X_1, \cdots, X_n)\otimes (Z_1, \cdots, Z_l) \to (Y_1, \cdots, Y_m)`$

面倒です。もちろん、文脈から $`X, Y, Z`$ が分かっているときは $`A_{\cup}`$ を使ってもかまいません。

「ストリング図とテンソル計算： クソバカ丁寧編」は一般的な行列・テンソルの話でしたが、マルコフ行列／マルコフテンソルのときは、確率に特有なワイヤーベンディング・オペレーターが登場します。それは条件化〈conditionalization〉オペレーターです。

条件化オペレーターもワイヤーベンディングとして描かれますが、行列・テンソルのプロファイルを変えるだけのワイヤーベンディング・オペレーターと条件化オペレーターは別物です。混同しないように注意してください。

また、「ストリング図とテンソル計算： クソバカ丁寧編」では行列の転置を話題にして、行列 $`A`$ の転置行列を $`A^\dagger`$ と書きました。ベイズ確率の文脈では、$`A^\dagger`$ はベイズ反転を意味します。単なる転置とベイズ反転も別物です。

別物に同じ記号を流用するのは混乱の弊害がありますが、構造的類似性を示唆するというメリットもあります。

同時確率分布の条件化

同時確率分布は、$`() \to (X, Y)`$ というプロファイルのテンソルで表現できます。ただし、確率なので「足して 1」という条件がつきます。

$`\quad Q:() \to (X, Y)\\
\quad Q = Q\Idx{*}{x, y}_{x\in X, y\in Y}\\
\Where\\
\quad \sum_{x\in X, y\in Y} Q\Idx{*}{x, y} = 1
`$

同時確率分布のテンソル $`Q`$ を単純に "lower left bending" したものを $`{_\vee Q}`$ 、条件化したものを $`{_\cup Q}`$ とします。単純なワイヤーベンディング・オペレーターと確率的な条件化が一緒に出てくるので、さすがに同じ記法〈象形文字〉は使えません。

$`{_\vee Q}`$ の成分は：

$`\quad {_\vee Q}\Idx{x}{y} = Q\Idx{*}{x, y}`$

これは、マルコフテンソル〈確率的なテンソル〉の条件を満たすとは限りません。が、（確率的な）正規化〈normalization〉をしてやればマルコフテンソルになります。正規化をするオペレーターを $`\mathrm{Norm}`$ とすると、その定義は次のようです*1。

$`\For A = A\Idx{x}{y}^{x\in X}_{y\in Y} : X \to Y\\
\:\\
\Define \mathrm{Norm}(A)\Idx{x}{y} :=
(\sum_{t\in Y}A\Idx{x}{t})^{-1} A\Idx{x}{y}
`$

"lower left bending" と正規化を使って、同時確率分布 $`Q`$ の条件化 $`{_\cup Q}`$ は次のように定義できます。

$`\For Q = Q\Idx{*}{x, y}_{x\in X, y\in Y} : () \to (X, Y)\\
\:\\
\Define {_\cup Q} := \mathrm{Norm}({_\vee Q})
`$

その成分は次のようになります。

$`\quad {_\cup Q}\Idx{x}{y} =
(\sum_{t\in Y}Q\Idx{*}{x, t})^{-1} Q\Idx{*}{x, y}
`$

おわりに

以下の過去記事

• ストリング図とテンソル計算： クソバカ丁寧編
• ストリング図と相性が良いテンソル計算 1/2

それと本記事「ストリング図と相性が良いテンソル計算 2/2」をジックリと読んで、実例にあたって記述と計算の練習をすれば、ストリング図とテンソル計算は不自由なく扱えるようになるだろうと思います。

*1:定義内に逆数が出てきます。ゼロの逆数は取れないので問題があります。しかし、確率の話では almost surely equal の同値関係により、ゼロの逆数の問題は解消します。