思いつきのメモ。
7月22日の記事「状態遷移系達の二重圏の直接的定義」において、マイヤース〈David Jaz Myers〉の圏論的システム理論〈categorical systems theory〉を紹介しました。7月22日記事において、「違和感/ズレ」という言葉を何度も使っています。「バックエンドとラッパー」の節で、「システムの定義が一様すぎるので直感と合わない」といったことを述べました。
その後、自分のなかの違和感/ズレを整理してみて、多次元の圏の捉え方に違和感/ズレを感じているのだ、と分かりました。マイヤースは、制御方向と準同型方向のニ方向を定式化していますが、僕は制御方向と入出力方向、それとモノイド積の方向を想定していたのでした。
システムの定式化には次の四方向が必要になると思われます。
- 制御方向
- 準同型方向
- 入出力方向
- モノイド積方向
グロタンディーク二重構成では、制御方向と準同型方向しか出てこないので、入出力方向/モノイド積方向の不在から違和感/ズレを感じたわけです。
最終的には4つの方向すべてを扱う必要があるでしょうが、どの方向から優先的に取り組むかの選択により様相は変わります。マイヤースは、制御方向と準同型方向を一度に構成できる、矢鱈に汎用的で強力な大道具であるグロタンディーク二重構成に魅力と可能性を感じたのでしょう。
僕の個人的感覚で言えば、汎用のグロタンディーク二重構成には幾つかの不満があります。
- 抽象的過ぎる。
- 既に述べたように、入出力方向とモノイド積方向が扱えない。
- モノイド積が扱えないので、トレースも扱えない。
- ペースティング図による計算は出来るが、ストリング図による計算がうまくいかない。
- ペースティング図による計算は複雑になりがち。
- 実際のシステムに関する素朴な直感があまり効かない。
そこで、準同型方向はとりあえず捨てて、入出力方向、制御方向、モノイド積方向の三方向を考えます。グロタンディーク二重構成のような大道具は使わずに、出来るだけ素朴かつ直接にシステム概念を定式化することにします。$`\newcommand{\mbf}[1]{\mathbf{#1}}
\newcommand{\In}{\text{ in }}
`$
システムをストリング図で表すときは、システムのボックスに対して、入力のワイヤー、出力のワイヤー、制御のワイヤーの3本のワイヤーが繋がった絵を描きます。
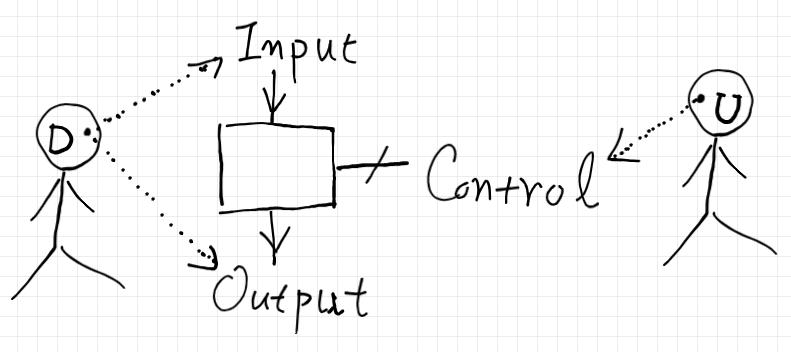
上の図で、入力から出力への方向は上から下です。制御のワイヤーは横に飛び出しています。制御は双方向通信になるので方向の矢印はあえて書かないことにします。制御ワイヤーの斜線は、それが制御ワイヤーであることを示す符丁です。
スティックマン U(User のつもり)からは、制御インターフェイスのみが見えます。一方、スティックマン D(Designer のつもり)からは、入出力のインターフェイスが見えています。スティックマン D は、複数のシステム(ボックス)の入出力を繋げて、より複雑なシステムを構成する人です。他に、制御インターフェイス〈ユーザーインターフェイス〉側で設計・構成の仕事をする人がいるかも知れません。
システムは、複数の入力ワイヤー、複数の出力ワイヤー、複数の制御ワイヤーを持ってもかまいません。以下の図は、システム $`\Phi`$ とシステム $`\Psi`$ をワイヤリングして組み合わせたものですが、全体としては、2本の入力ワイヤー、2本の出力ワイヤー、2本の制御ワイヤーを持つ複合システムになっています。
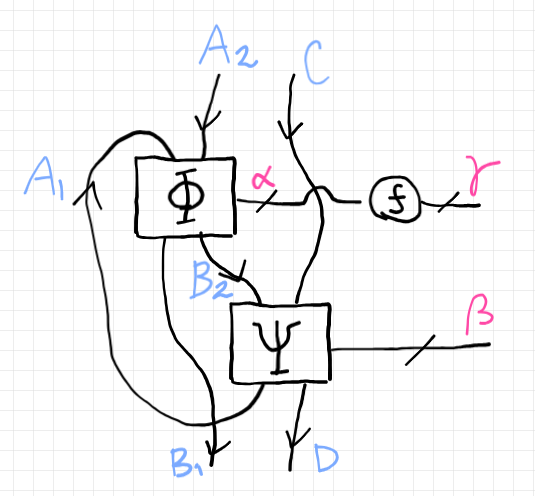
四角い箱のワイヤリングは、トレース付き対称モノイド多圏〈traced symmetric monoidal polycategory〉(「述語論理: 様々な多圏達の分類整理」参照)の流儀で行います。
丸いノード $`f`$ はレンズ射です。レンズ射を右側横方向に繋ぐことができます。システム(四角い箱)とレンズ射、あるいはレンズ射とレンズ射はレンズ結合〈lens composition〉で横方向に連結できます。
入力・出力・制御のインターフェイスを持つシステム(四角い箱)をIOCシステム〈IOC system〉と呼ぶことにして、IOCシステム達の圏を $`\mbf{IOCSys}`$ とすると、複合システムの素材となった $`\Phi, \Psi`$ のプロファイルは次のように書けます。
$`\quad \Phi: (A_1, A_2)\to (B_1, B_2) \text{ ctrl }\alpha \In \mbf{IOCSys}\\
\quad \Psi: (B_2, C)\to (A_1, D) \text{ ctrl }\beta \In \mbf{IOCSys}
`$
$`\text{ctrl}`$ に続けて制御インターフェイス(実体はバンドル)を書いています。
横方向に繋いだレンズ射(制御インターフェイスのラッパー)$`f`$ のプロファイルは次です。
$`\quad f: \alpha \to \gamma\In \mbf{Lens}
`$
この定式化では、IOCシステムもレンズ射も圏の射になっています(対象ではない)。$`\mbf{IOCSys}`$ と $`\mbf{Lens}`$ は異なる圏であるにも関わらず、異なる圏に属する射達を結合できます。ニ種類の射達とニ種類の結合、そして異種の射の結合を持ちますが、全体として二重圏というわけでもありません。
モノイド積(具体例ではデカルト積)は、図の左側(圏 $`\mbf{IOCSys}`$ の側)では横方向の併置で、図の右側(圏 $`\mbf{Lnes}`$ の側)では縦方向の併置で表現されます。
2つのモノイド圏が、違う方向に広がりながらも、互いに絡み合う構造になっています。ちょっと奇妙な構造ですが、バックエンドとラッパーの直感(「バックエンドとラッパー」参照)には合っています。
グロタンディーク二重構成にさらに構造を付け足せば、おそらく同じことは出来るでしょうが、素朴かつ直接的で、ただちにストリング図描画が可能である点では、$`\mbf{IOCSys} + \mbf{Lens}`$ 方式にも意味はあるでしょう。
思いつきを記したのですが、この思いつきをちゃんとした形にするのはだいぶ難しいようです。
入出力によって結合した複合システム $`\Phi; \Psi`$ の制御インターフェイスをどう定義すべきか? これは難しいですね。「内部構造は隠蔽すべし」というブラックボックス原理と整合するように、複合システムの制御インターフェイスを定義するのが困難。
この困難さには関数の決定性の要求も絡んでいるので、決定性の要求を諦めることも考えられます。が、そうすると、非決定性に伴う煩雑さ/面倒さを抱え込むことになります。
あちらを立てればこちらが立たずな状況です。
[/追記]