IOCシステムと制御ラッパーの構造 - 檜山正幸のキマイラ飼育記 (はてなBlog)

「マイヤースのシステム理論への違和感と代替案」で述べたIOCシステム〈入力・出力・制御付きシステム〉と、制御インターフェイスへのラッパーについて、具体的な定義を提示します。背景となる圏は集合圏としますが、デカルト圏や対称モノイド圏への拡張は難しくないと思います。$`%\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mbf}[1]{\mathbf{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
%\newcommand{\msc}[1]{\mathscr{#1}}
\newcommand{\mbb}[1]{\mathbb{#1}}
\newcommand{\In}{\text{ in }}
%\newcommand{\twoto}{\Rightarrow }
%\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id}}
%\newcommand{\u}[1]{\underline{#1}}
\newcommand{\o}[1]{\overline{#1}}
\newcommand{\hyp}{ \text{－} }
%\newcommand{\Iff}{ \Leftrightarrow }
%\newcommand{\Imp}{ \Rightarrow }
\newcommand{\base}[1]{ {{#1}\!\lrcorner} }
\newcommand{\Bun}[2]{ \begin{bmatrix} {#1}\\ \downarrow\\{#2}\end{bmatrix} }
%\newcommand{\BunM}[2]{ \begin{bmatrix} {#1}\\{}\\{#2}\end{bmatrix} }
%\newcommand{\BunF}[2]{ \begin{pmatrix} {#1}\\{}\\{#2}\end{pmatrix} }
\newcommand{\LensM}[2]{ \begin{pmatrix} {#1}\\{\leftarrow}\\{#2}\end{pmatrix} }
`$

内容：

バンドルとレンズ射の圏
IOCシステム
実例：オートマトン
斜反ファイブレーション

ハブ記事：

状態遷移系達の二重圏の直接的定義

バンドルとレンズ射の圏

バンドル達とバンドル射の圏 $`\mbf{Bun}`$ と、バンドルを対象としてレンズ射を射とする圏 $`\mbf{Lens}`$ については、7月22日の記事に書いています。

ここでは、圏 $`\mbf{Bun}`$ より圏 $`\mbf{Lens}`$ を使います。

圏 $`\mbf{Lens}`$ の対象（バンドル）は $`\alpha, \beta`$ などと書く。
バンドル（$`\mbf{Lens}`$ の対象）を集合圏に展開した場合は $`\alpha: \o{\alpha}\to\base{\alpha}\In \mbf{Set}`$ とか $`\alpha: \o{\alpha}\to A\In \mbf{Set}`$ と書く。
レンズ射 $`f:\alpha \to \beta\In \mbf{Lens}`$ を集合圏に展開した場合は、以下の図式として描く。

$`\quad \xymatrix@C+1pc{
{\o{\alpha} }\ar[d]_\alpha
\ar@{}[dr]|{\text{comm.}}
&{f^* \o{\beta}} \ar[d]|{f^* \alpha}
\ar[l]_{f^\sharp}
\ar[r]^{f^\uparrow}
\ar@{}[dr]|{\text{p.b.}}
&{\o{\beta}} \ar[d]^\beta
\\
A \ar@{=}[r]
&{A} \ar[r]_f
&{B}
}\\
\quad \In \mbf{Set}
`$

次のような記号の乱用を使っています。

$`\quad f = \LensM{f^\sharp}{f} : \Bun{\o{\alpha}}{A} \to \Bun{\o{\beta}}{B}\In \mbf{Lens}`$

記号の乱用とベース空間の一文字への置き換えを使わないなら次のようです。

$`\quad f = \LensM{f^\sharp}{\base{f}} : \Bun{\o{\alpha}}{\base{\alpha} }\to \Bun{\o{\beta}}{\base{\beta} }\In \mbf{Lens}`$

$`f^\uparrow`$ を正確に書くなら：

$`\quad f^\uparrow = \base{f}^{\uparrow \beta} \; : f^* \o{\beta} \to \o{\beta}\In \mbf{Set}`$

レンズ射の左側の可換四角形を三角形で描いたり、全体をホームベース形に描くこともあります（「状態遷移系はホームベース形に描くと良い」参照）。

IOCシステム

「マイヤースのシステム理論への違和感と代替案」で例に挙げた次の複合IOCシステムを題材に使います。

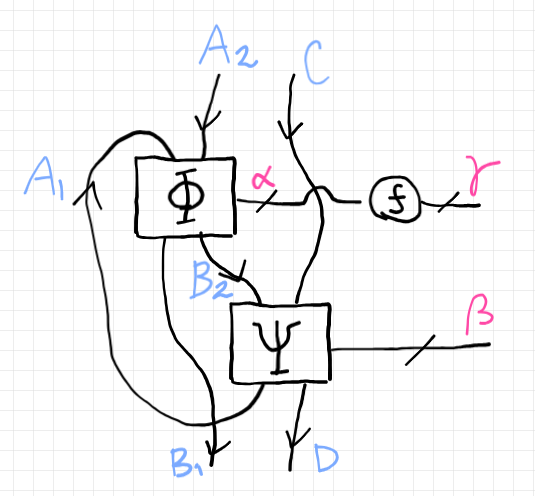
構成素の集合・関数がたくさんあるので、文字・フォントの管理が大変です。ピンク色はバンドルですが、バンドル $`\gamma`$ のベース空間を $`C`$ と置くと、IOCシステム $`\Psi`$ の入力の集合 $`C`$ と被ってしまいます。バンドルのベース空間をラテン文字大文字に置き換えるのはやめて $`\base{\gamma}`$ を使います。

IOCシステムは、「レンズ射は状態遷移系である // 状態遷移系達の二重圏の直接的定義」で説明した、状態遷移系としてのレンズ射を変更したものです。

内部移動空間はそのままですが、内部状態空間の代わりに入力空間と出力空間の2つの集合を考えて、次のような入出力スパン〈input-output span〉を作ります。

$`\quad \xymatrix{
{A_1\times A_2}
&M \ar[l] \ar[r]
&{B_1\times B_2}
}\\
\quad \In \mbf{Set}
`$

これは、IOCシステム $`\Psi`$ の入出力スパンです。集合 $`M`$ がシステムの内部移動空間〈internal move space〉です。入力空間〈input space〉 $`{A_1\times A_2}`$ と出力空間〈output space〉 $`{B_1\times B_2}`$ は複合システムの設計者からは見えているので、完全に内部的で隠蔽されているのは内部移動空間（スパンのボディ）だけです。入出力を与えるスパンは、入力から出力への対応〈遷移〉の可能性を記述するものです。可能性なので、記述は非決定性を持てます。

[追記]
IOCシステムの図式の左側の可換四角形を次のように書いていました。

$`\quad \xymatrix@C+1.5pc{
{M} \ar@{=}[d]
\ar@{}[dr]|{\text{comm.}}
&{{\ell_\Phi}^* \o{\alpha}} \ar[d]|{ {\ell_\Phi}^* \alpha}
\ar[l]_{{\ell_\Phi}^\sharp}
\\
M \ar@{=}[r]
&M
}
`$

これは、$`{\ell_\Phi}^* \alpha = {\ell_\Phi}^\sharp`$ という等式であり、状態遷移系としては意味がなくなってしまいます。次のような可換四角形に修正しました。

$`\quad \xymatrix@C+1.5pc{
{M} \ar[d]
\ar@{}[dr]|{\text{comm.}}
&{{\ell_\Phi}^* \o{\alpha}} \ar[d]|{ {\ell_\Phi}^* \alpha}
\ar[l]_{{\ell_\Phi}^\sharp}
\\
{A_1\times A_2} \ar@{=}[r]
&{A_1\times A_2}
}
`$

[/追記]

IOCシステム $`\Phi`$ は、その一部として次のレンズ構造を持ちます。

$`\quad \xymatrix@C+1.5pc{
{M} \ar[d]
\ar@{}[dr]|{\text{comm.}}
&{{\ell_\Phi}^* \o{\alpha}} \ar[d]|{ {\ell_\Phi}^* \alpha}
\ar[l]_{{\ell_\Phi}^\sharp}
\ar[r]^{ {\ell_\Phi}^\uparrow}
\ar@{}[dr]|{\text{p.b.}}
&{\o{\alpha}} \ar[d]^\alpha
\\
{A_1\times A_2} \ar@{=}[r]
&{A_1\times A_2} \ar[r]_{\ell_\Phi}
&{\base{\alpha} }
}\\
\quad \In \mbf{Set}
`$

一番左の縦方向の無名の矢印は、入出力スパンの左脚です。

$`\quad \ell_\Phi = \LensM{{\ell_\Phi}^\sharp}{\ell_\Phi} : \Bun{M }{A_1\times A_2 } \to \Bun{\o{\alpha}}{\base{\alpha}} \In \mbf{Lens}`$

ここで、$`\ell_\Phi`$ はシステム $`\Phi`$ の露出関数〈expose function〉です。露出関数は、入力空間 $`A_1\times A_2`$ から外部状態空間 $`\base{\alpha}`$ への関数とします。

$`\quad \ell = \ell_\Phi : {A_1\times A_2} \to \base{\alpha} \In \mbf{Set}`$

露出関数により、IOCシステム内部の情報の一部は制御インターフェイス $`\alpha`$ の利用者に開示されます。

レンズ射の逆行ファイバーパートである $`{\ell_\Phi}^\sharp`$ は、（状態更新関数ではなくて）移動生成関数〈move generate function〉と呼ぶことにします。移動生成関数は、制御情報から移動（内部移動空間 $`M`$ の要素）を生成します。移動は、入力を出力へと遷移させる方法をカプセル化したデータです*1。

上の絵の複合システムでは、IOCシステム $`\Phi`$ に制御インターフェイスのラッパーであるレンズ射 $`f`$ を結合しています。この部分を取り出してホームベース形のペースティング図に描くと次のようです。

$`\quad \xymatrix{
{}
&{}
&{{\ell_\Phi}^{\uparrow *}(f^*\o{\beta}) }\ar[dl]_{{\ell_\Phi}^{\uparrow *}f^\sharp }
\ar[dr]^{{\ell_\Phi}^{\uparrow \uparrow}}
\ar@{}[dd]|{\text{p.b.}}
&{}
&{}
\\
{}
&{{\ell_\Phi}^*\o{\alpha}} \ar[dl]_{{\ell_\Phi}^\sharp}\ar[dr]^{{\ell_\Phi}^\uparrow}\ar[ddl]
\ar@{}[dd]|{\text{p.b.}}
&{}
&{f^*\o{\beta}} \ar[dl]_{f^\sharp}\ar[dr]^{f^\uparrow}\ar[ddl]
\ar@{}[dd]|{\text{p.b.}}
&{}
\\
{M} \ar[d]
&{}
&{\o{\alpha}} \ar[d]
&{}
&{\o{\beta}} \ar[d]
\\
{A_1\times A_2} \ar[rr]_{\ell_\Phi}
&{}
&{\base{\alpha} } \ar[rr]_f
&{}
&{\base{\beta} }
}\\
\quad \text{commutative }\In \mbf{Set}
`$

左側のレンズ射はIOCシステム $`\Phi`$ の一部です。右側のレンズ射 $`f`$ は、制御インターフェイス $`\alpha`$ を別な制御インターフェイス $`\beta`$ に変換する制御インターフェイス・ラッパーです。横方向への結合はすべてレンズ結合です。

IOCシステムのあいだの入出力結合〈input-output composition〉は、ストリング図ではワイヤリングにより記述されています。ワイヤリングの集合圏における解釈は集合係数のテンソル計算で与えられます。IOCシステムとレンズ射〈制御ラッパー〉が混じった計算は、集合係数のテンソル計算とレンズ計算のハイブリッドになります。

実例：オートマトン

$`\mbf{IOCSys+Lens}`$ により定式化できる具体例として、形式言語理論に出てくるオートマトンを取り上げます。

形式言語理論／オートマトン理論の伝統では、ラベル付き遷移系〈labeled transition system〉のラベル達の集合をアルファベット〈alphabet〉と呼び $`\Sigma`$ と書きます。おそらく、symbol の 's' に対応するギリシャ文字大文字だからでしょう。状態空間〈state space〉はなぜか $`Q`$ が多いですが、ここでは $`S`$ とします。

遷移関数〈trnsition function〉も伝統に従い $`\delta : S\times \Sigma \to S\In \mbf{Set}`$ とします。終状態〈{final | terminal} state〉かどうかを確認する述語を $`h:S \to \mbf{B}\In\mbf{Set}`$ とします。 $`\mbf{B} = \{0, 1\}`$ は二値真偽値の二元集合です。終状態達の集合は次のように書けます。

$`\quad \{s\in S\mid h(s) = 1\} \subseteq S`$

ここでは、初期状態は考えません。オートマトン〈automaton〉は $`(\Sigma, S, \delta, h)`$ と書けます。

与えられたオートマトンから、IOCシステムを構成します。IOCシステムの定義には次が必要です。

入出力スパン（スパンのボディは内部移動空間）
制御インターフェイス・バンドル
内部構造である露出関数と移動生成関数

まず、入出力スパンは：

$`\quad \xymatrix{
S
&{S\times S} \ar[l]_{\pi_1} \ar[r]^{\pi_2}
&S
}\\
\quad \In\mbf{Set}
`$

スパンの左右の脚は第一射影と第二射影です。ボディである内部移動空間は、$`(s, s')`$ という“可能な移動〈遷移〉”を表わすペア。今の場合、任意の状態から任意の状態への移動が可能です。

次に制御インターフェイス・バンドルは以下のようです。

$`\quad \pi_1 : \mbf{B}\times \Sigma \to \mbf{B}\In \mbf{Set}`$

これも第一射影です。外部状態（$`0`$ または $`1`$）に関わらず同じ記号〈コマンド〉が使えます。

IOCシステムの内部構造である露出関数と移動生成関数は次のようです。

$`\quad \xymatrix{
{S\times S} \ar[d]_{\pi_1}
\ar@{}[dr]|{\text{comm.}}
&{S\times\Sigma} \ar[d]|{\pi_1} \ar[r]^{h\times \id_\Sigma}
\ar[l]_{\langle \pi_1, \delta\rangle}
\ar@{}[dr]|{\text{p.b.}}
&{\mbf{B}\times \Sigma} \ar[d]^{\pi_1}
\\
{S} \ar@{=}[r]
&{S} \ar[r]_{h}
&{\mbf{B}}
}\\
\quad \In \mbf{Set}
`$

$`\langle \pi_1, \delta\rangle`$ は第一射影と遷移関数のデカルト対〈Cartesian pairing〉で次のように計算します。

$`\text{For }(s, \sigma)\in S\times \Sigma\\
\quad \langle \pi_1, \delta\rangle(s, \sigma) := (s, \delta(s, \sigma))
`$

オートマトンに限らず、Command-Query分離されたインターフェイス（「メイヤー先生の偉大さとCommand-Query分離」参照）を持つシステムはIOCシステムと考えることが出来ます。

このようにして、「オートマトン $`\mapsto`$ IOCシステム」という写像は作れますが、オートマトンのあいだの準同型射を移す先はありません。それは、圏 $`\mbf{IOCSys}`$ を作るときに準同型方向を捨ててしまった（定式化を諦めた）からです。将来的には準同型方向を付け足すことが必要です。

斜反ファイブレーション

$`\mbf{IOCSys+Lens}`$ という構造は、どのような圏論的構造物なんでしょうか？

IOCシステムとレンズ射というニ種類の射を持つが、二重圏にはなっていない。
IOCシステムにその制御インターフェイスを対応させる写像〈関数〉は在るが、関手にはなってない。
反ファイブレーション／余インデックス付き圏の構造を持つ。

2-圏達の3-圏内に居る2-ファイブレーションとかを使うとうまく定式化できるのかな？と思ったりしますが、現状はよく分かりません。しかし、IOCシステムにその制御インターフェイスを対応させる写像 $`\mrm{Ctrl}`$ と、反ファイブレーション／余インデックス付き圏の構造を公理化することはできそうです。

[追記]
以下に出てくる
$`\quad \mrm{Ctrl}(\Phi ; \Psi) \cong \mrm{Ctrl}(\Phi)\times \mrm{Ctrl}(\Psi)`$
は、ウマクないです。考え直す必要があります。

$`\mrm{Ctrl}(\Phi ; \Psi)`$ をうまいこと定義するのは難しいです（マイヤースのシステム理論への違和感と代替案の追記も参照）。
[/追記]

$`\mrm{Ctrl}`$ の性質をまとめましょう。圏 $`\mrm{Lens}`$ はデカルト積を持ちます。デカルト積の単位対象を $`\mbb{I}`$ とします。次の同型（等式と思ってもよい）があります。

$`\quad \mrm{Ctrl} : \mrm{Mor}(\mbf{IOCSys}) \to |\mbf{Lens}|\In \mbf{SET}\\
\text{For }\Phi, \Psi \in \mrm{Mor}(\mbf{IOSys})\\
\text{When }\mrm{cod}(\Phi) = \mrm{dom}(\Psi)\\
\quad \mrm{Ctrl}(\Phi ; \Psi) \cong \mrm{Ctrl}(\Phi)\times \mrm{Ctrl}(\Psi)\\
\quad \mrm{Ctrl}(\id_\Phi) \cong {\mbb{I}}
`$

また、次の余インデックス付き圏〈反インデックス付き圏〉があります。

$`\quad \mrm{Ctrl}_{\to} : \mbf{Lens} \to \mbf{CAT} \In 2\mbb{CAT}`$

$`f:\alpha \to \beta \In \mbf{Lens}`$ に対して、次のようになります。

$`\quad \mrm{Ctrl}_{\to}(f) : \mrm{Ctrl}^{-1}(\alpha) \to \mrm{Ctrl}^{-1}(\beta)
\In \mbf{CAT}
`$

ここで、$`\mrm{Ctrl}^{-1}(\hyp)`$ は、写像 $`\mrm{Ctrl}`$ の逆像集合です。逆像集合から離散圏または余離散圏を作って圏だとみなします。

$`f_* := \mrm{Ctrl}_{\to}(f)`$ と略記するとして、$`f_* \Phi = f_*(\Phi)`$ は、IOCシステム $`\Phi`$ の制御インターフェイスにレンズ射 $`f`$ を“横向き”に結合することです。

$`\mrm{Ctrl}`$ と $`\mrm{Ctrl}_{\to}`$ から抽象化した公理的構造を（ちゃんと定義してないですが）斜反ファイブレーション〈skew opfibration〉と、とりあえず呼んでおきましょう。反ファイブレーションとけっこう似てますが、少しゆがんでいる印象があるからです。

[追記]
この記事執筆時点で僕が想定していた斜反ファイブレーションにより、IOCシステムと制御インターフェイスの関係を記述できるかは怪しいです。簡単じゃない、考えるべき点が色々あります。

マイヤースのシステム理論への違和感と代替案の追記も参照。
[/追記]

前節で述べたように、$`\mbf{IOCSys+Lens}`$ が持つ斜反ファイブレーション構造に対して準同型方向を付け足すことが必要です。すると、3次元的な圏（モノイド積方向も入れると4次元的な圏）となります。それは、なんらかのファイブレーション（あるいはインデキシング）構造を持ちます。

「状態遷移系達の二重圏の直接的定義」より：