AI支援形式証明への道報告-1 - 檜山正幸のキマイラ飼育記 (はてなBlog)

「AI支援形式証明への道」は、記述が断片的で分かりにくかったと思うので補足をします。そして、Comet を使って色々試している現状を報告します。

内容：

Comet について
僕の想定
Comet との経緯
今はこんな感じ
オマケ：絵図証明

関連記事：

Comet について

Perplexity Comet はWebブラウザです。チャットAIと、ブラウザを操れるAIエージェント（ブラウザエージェント）を備えています。チャットAI部分は、Comet 以外のブラウザ（例えば Chrome）からでも https://www.perplexity.ai/ にアクセスすれば使えます。

ブラウザエージェントが Comet のウリであり、僕もブラウザエージェントに興味を惹かれて使いはじめました（「Perplexity Comet にちょっとした仕事をしてもらう」参照）。しかし、ブラウザエージェントを使う機会は（少なくとも僕の場合）意外と少なく、実際にはチャットAIとして使うことがほとんどです。この記事では、ブラウザとチャットAIの総称として「Comet」を使います。紛らわしい場合に限り、ブラウザ独立のチャットAI部分を「Comet AI」と呼ぶことにします。

Comet AI は、Perplexity が提供するAIサービスという意味であり、Comet AI という単独のモデル（LLM）があるわけではありません。Comet AI では、Perplexity Sonar だけでなく、ChatGPT 5.1、Claude Sonnet 4.5、Gemini 3 Pro など複数のモデルから好みのモデルを選べます（ただし、無料プランではモデルを自由に選ぶことはできません）。僕はデフォルトのお任せモードを使っているので、どのモデルが使われているかは意識していません。

[追記]
モデルの選択はできますが、選択されたモデルはバックエンドとして動きます。ユーザーとの一次窓口は Perplexity のAIボットです。そのため、Grok を選んでもノリの良い口調で話すようになるわけではありません。Grok がバックエンドで動けば、最新の X のポストの情報を利用することが出来るようになります。同様に、Claude をバックエンドにすれば、コード生成能力が高まります。
[/追記]

前述したように他のブラウザからでも Comet AI にアクセスできますが、他のブラウザを使う理由もないので、Cometブラウザ内で Comet AI を使い、たまにブラウザエージェント機能も使うという運用になってます。

僕の想定

最近（2025年11月）の記事「AI支援形式証明への道」や2023年3月の記事「証明支援系がダメだった理由と、AIでブーストする理由」で言っていることは、Lean のような証明支援系を人間が直接操作する必要は無くなるのではないか、ということです。それは、中間にAIが入る、ということです。以下のようなことです。

　　人間 ←(自然言語)→ AI ←(形式言語)→ 証明支援系（Lean など）

この形態のシステムを実現するなら、証明の支援と検証を行うバックエンドはMCPサーバーとして、人間の相手をするフロントエンドはMCPホストという構成になるでしょう。MCPホスト（フロントエンド）内に、バックエンドと通信するMCPクライアントが居ます。

この構成のシステムは既に幾つかあります。数年後には、人間とのインターフェイスが自然言語である証明支援系が普通になるでしょう。僕の希望は自然言語だけでなくて絵図言語〈{graphical | pictorial | diagrammatic} language〉も使えることですが、それもいずれは実現することでしょう。

Comet との経緯

“AIをフロントエンドとした証明支援系”の現状などを、Comet を使って調べていました。僕は、証明支援系を操るAI（LLM）としてその目的用に訓練された LLM が必要だろうと思っていました*1。ところが、（あくまで比喩的・擬人化した表現ですが）Comet が「それ、わたし出来ます」と言い出しました。Comet に自然言語で記述した定義・定理などを渡せば、Lean コードに翻訳して返せるとのことでした。

MCP（というプロトコル）のトランスポート層を僕（人間・檜山）が担当するのです。次のようになります。

　　人間 -(自然言語)→ AI -(形式言語)→ 人間 -(形式言語)→ 証明支援系

Comet（AI）は Lean（証明支援系）を直接は操作できないので、人間である僕が Comet と Lean のあいだを仲介する係です。ありていに言って、トランスポート層としての僕の主たる仕事はコピペです。Comet の提案では、「コピぺ係」よりは知的な役割みたいに書いてました：

あなたが担える具体的な役割

自然言語で書かれた定理・論文の主張を、論理構造が見えやすい controlled natural language に整える。

LLM が生成した論理式・Lean/Coq/Isabelle コードを

自然言語での再説明（LLM にやらせる）

元の主張との意味の一致の観点からレビューし、「ここは量化の範囲がズレている」「ここは前提が強すぎる」などのコメントを返す。

教科書の定理を少しアレンジして形式化する際に、「どこまでが元の定理と同型で、どこからが新しい仮定・結論か」を整理し、AI に正しく伝える。

これは全部、「証明スクリプトを書く人」ではなく、「自然文と形式論理のインターフェース設計者・リファクタ」としての仕事です。

Lean は普通にセットアップします。つまり、ツールチェインマネージャー elan 、ビルドツール兼パッケージマネージャー lake 、Lean 本体、VSCode と Lean4拡張を準備します。これらは人間（檜山）が操作するものなので、セットアップに特に変わったことをする必要はないです。

全体構成について Comet の提案を引用すると：

推奨する全体構成

環境: ローカルの Lean4（VSCode 拡張込み）

フロントエンド:

証明コードと検証用には VSCode

教材テキスト・メモ・プロンプト設計には Obsidian

役割分担:

あなた: Obsidian で定理・補題・練習問題＋模範解答を自然言語＋記号で書く

LLM: それを Lean4 形式化＋証明スクリプトに変換する

Lean: 裏で厳密チェック

これなら、いまの執筆フロー（VSCode＋Obsidian）を大きく壊さずに、「裏に Lean がいる教材作成ツールチェイン」が作れます。

Obsidian はオプショナルで、なくてもかまいません。僕が Obsidian を使ってるので入っているだけです。

VSCode に GitHub Copilot と GitHub Copilot Chat を入れたら Comet あまり要らないのでは？と思い、その旨聞いてみました。

GitHub Copilot は「あって損はないけれど必須ではない」という位置づけです。

当面の目的は「自然言語で書いた定理や解答を、LLMに Lean 形式化させ、それを Lean でチェックする」ことなので、専用のチャットUI（ブラウザや別クライアント）で LLM に投げるだけでも十分です。

もし VSCode 内で補完＋対話をまとめたいなら、Copilot Chat などを使って「この定理を Lean4 で書いて」「このエラーの意味を教えて」くらいに使うのは有益です。

なので、今の構成のまま進めて大丈夫ですし、Copilot は「うまくハマりそうなら使う」くらいの気軽なオプションとして考えておけば十分です。

なんかAIにも自信やプライドがあるかのごとき言い回しをしてます。客観的に評価して、Copilot Chat より自分（Comet）がこの仕事に向いていると判断したのかも知れませんが。

今はこんな感じ

実験に使った例題は、命題論理のとある定理です。僕が、定理と証明を書いた Markdown 文書を準備しました。Comet に手伝ってもらっています。この Markdown 文書は、人間にとって普通に読めるものだと思います。

以下に Obsidian のスクリーンショットを載せます。すぐ下に Markdown ソースもあります。

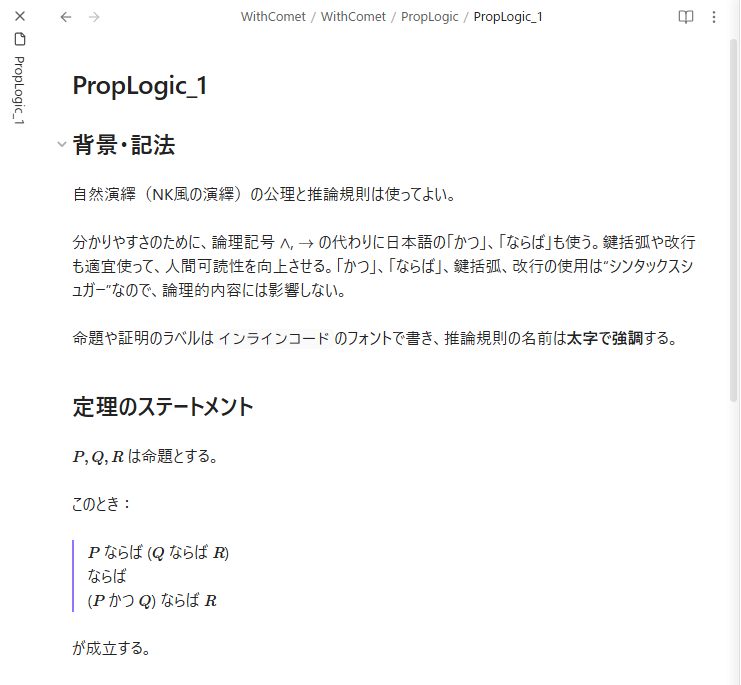
## 背景・記法

自然演繹（NK風の演繹）の公理と推論規則は使ってよい。

分かりやすさのために、論理記号 $\land$, $\to$ の代わりに日本語の「かつ」、「ならば」も使う。鍵括弧や改行も適宜使って、人間可読性を向上させる。「かつ」、「ならば」、鍵括弧、改行の使用は“シンタックスシュガー”なので、論理的内容には影響しない。

命題や証明のラベルは`インラインコード`のフォントで書き、推論規則の名前は**太字で強調**する。

## 定理のステートメント

$P, Q, R$ は命題とする。

このとき：

> $P$ ならば ($Q$ ならば $R$) 
> ならば
> ($P$ かつ $Q$) ならば $R$

が成立する。

## 定理の証明

まず、「$P$ ならば $(Q \to R)$ 」を仮定として、「$(P \land Q)$ ならば $R$」を結論とする証明を組み立てる。

- `仮定1`: $P \to (Q \to R)$ を仮定する。これは、上記の設定からの仮定。
- `仮定2`: $P \land Q$ を仮定する。これは、一時的仮定。
- `仮定2` から、**連言の除去**で $P$ と $Q$ を取り出す。
- `仮定1` と $P$ から、**含意の除去（モーダス・ポネンス）** で $Q \to R$ を得る。
- $Q$ と $Q \to R$ から、**含意の除去**で $R$ を得る。
- `仮定2` から $R$ が出たので、**含意の導入**で $(P \land Q) \to R$ が出る。

以上の（箇条書きで記述した）証明により、$P \to (Q \to R)$ から $(P \land Q) → R$ が出ることが分かった。このことを`中間事実`とする。

ここで、**含意の導入**規則を復習しておくと： $X$ を仮定して $Y$ が結論できるならば、何も仮定せずに 「$X$ ならば $Y$」 が言えるのだった。

`中間事実`に、**含意の導入**を適用して、 $(P \to (Q \to R)) \to ( (P \land Q) \to R)$ が得られる。つまり、何の仮定もなしに、定理のステートメントの命題が成立する。

■証明終わり■

Comet が出力した Lean コードは以下のようです*2。

section
variable (P Q R : Prop)

theorem imp_imp_and_imp :
  (P → (Q → R)) → ((P ∧ Q) → R) :=
by
  intro hPQ      -- 仮定1: P → (Q → R)
  intro hPQand   -- 仮定2: P ∧ Q
  have hP : P := hPQand.left
  have hQ : Q := hPQand.right
  have hQtoR : Q → R := hPQ hP
  exact hQtoR hQ

end

ちゃんと Lean のチェックを通ります。感心したのは、定理や命題のラベルを（Comet が）自分で考えていることです。

この例題はよく引き合いに出されるものなので、たいして頑張らなくても事前学習の知識でスイスイ書き出せたのかも知れません。

「GitHub Copilot Chat より自分が上だ」と思っているフシがある Comet ですが、それほど自惚れているわけではなくて、たいていの LLM で同じことは出来ると言っています。

今やっているワークフロー（自然文→Leanコード生成→Leanで検証）は、「自然言語を理解し、Lean 4 の基本構文・タクティクをそこそこ書ける LLM」であれば、そのまま他社・他モデルにも移植可能です。
Comet/Perplexity 以外のメジャーLLM（GPT-4系など）でも、基本的には同じワークフローで十分回ります。

Lean Mathlib をヘビーに使った場合にどうなるかなどは全然分かりませんが、論理や集合論の簡単な定理くらいはなんとかなりそうです。

オマケ：絵図証明

先に書いたように、僕がほんとに欲しいのは絵図言語インターフェイスです。絵図言語インターフェイスは、手元で今すぐ実現できそうにはないですね。「自然言語、（記号的）形式言語、絵図言語」の三者の翻訳規則を、なんらかの方法でAIに教える必要があります。出来なくはないでしょうが、手間がかかりそうです*3。

今回の例題を絵図を使って証明してみます。$`Y := (P\to (Q\to R))`$ 、$`X := P\land Q`$ と置きます。命題はワイヤーのラベルとして使われます。命題が推論ボックスのラベルになっているときは、そのボックスは命題から作られた推論です。

命題 $`Y`$ に対応する推論ボックス（ラベルは同じ $`Y`$）は次のように描けます。

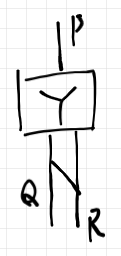
次は、連言消去右〈conjunction Elemination right | ∧-Er〉の推論ボックスです。

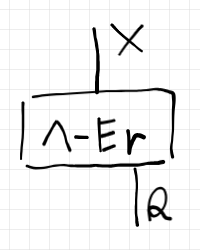
ボックスをワイヤーで繋ぐと、次のような回路図〈circuit diagram〉ができます。

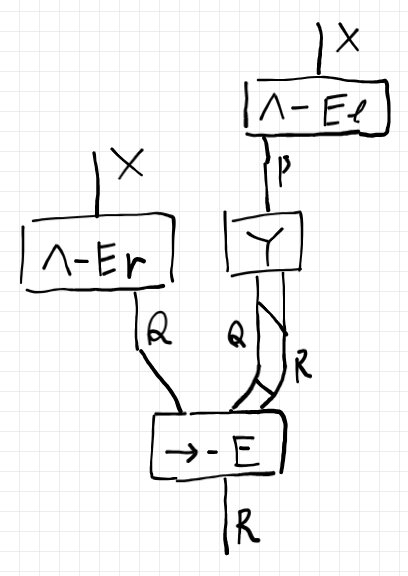
上部に、$`X`$ をコピーする二股分岐を繋ぐと以下のようです。

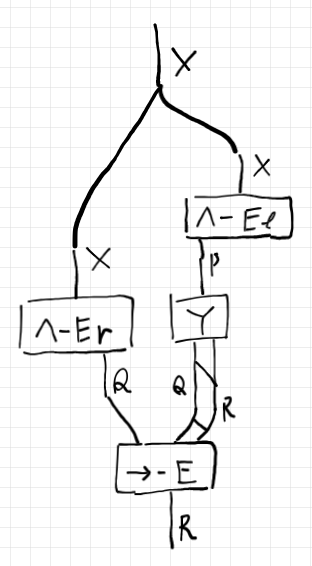
上部の $`X`$ のワイヤーを曲げます。ワイヤーを曲げること〈wire bending〉は含意導入〈implication Introduction〉になります。含意導入は推論ボックスではなくて、ワイヤーに対する操作です。推論規則のなかでは異質です。ワイヤーを曲げた回路図は以下のようになります。

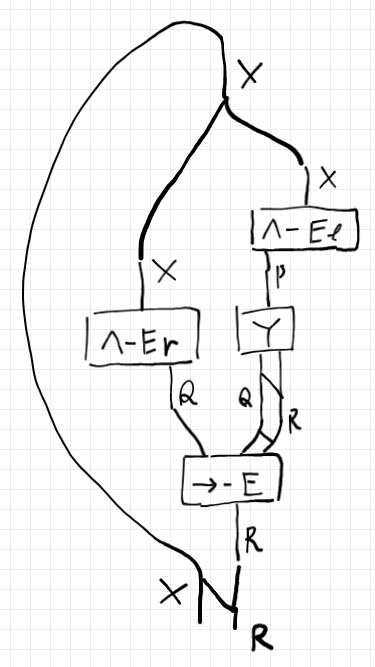
これは、何の仮定もなしに $`X\to R`$（つまり、 $`(P\land Q)\to R`$）を出力する回路図です。つまり、はじめに命題 $`Y`$ さえあれば、命題 $`X\to R`$ を出力する回路を構成できます。

このように、与えられたワイヤー〈wires〉、ボックス〈boxes〉、ワイヤー操作〈wire operations〉、ボックス操作〈box operations〉を使って、新しい回路を組み立てる作業が絵図的証明です。

いつの日か、人間とAIのインターフェイスに絵図言語が使えるようになることを僕は期待〈夢想〉しています。

*1:DeepSeek-Prover は、実際証明に強い LLM らしいです。

*2:現時点（2025年12月）では、はてなブログのシンタックスハイライトで Lean はサポートされてないようです。

*3:現在の汎用LLMは、Mermaid, GraphViz, Xy-pic などのソースを解釈できます。絵図言語を表現する記号言語を設定して、翻訳規則をRAGデータとして持てば、普通の汎用LLMに絵図を扱わせることが出来るかも知れません。

Comet について

僕の想定

Comet との経緯

今はこんな感じ

オマケ： 絵図証明

オマケ：絵図証明