自己関手の圏とモナド - 檜山正幸のキマイラ飼育記 (はてなBlog)

非対称なモノイド圏という概念

モナドの定義をモノイドとして再確認

これを、お絵描き計算（pictorial calculation）を使ってチャント（になるかな？）説明してみようか、と思いました。こういうことは一気にババッと書き切らないと、ヘタって後が続かないことが多いのですが、残念、本日は厳密モノイド圏の実例で息切れ。でもまー、お絵描きの準備はできたから、いいとしよう。

内容：

モナドはモノイドだ -- 言ってるだけ
循環的な状況が恐いけど魅力的
準備：ボックス図からストリング図へ
準備：徹底的に左から右の記法
自己関手の圏End(C)
余談：圏論は、ほぼ計算だけ
厳密モノイド圏
実例：行列の圏
実例：非負の実数
実例：釘にラベルが付いたブレイド図の圏
ほんとに面白いのは

モナドはモノイドだ -- 言ってるだけ

実は、「モナドはモノイドだ」ということは、アッチコッチで断片的に述べてます。「無理して(圏論的)モナドをJavaで説明してみる」の「モナドの効用」のところで、

モナド結合律とモナド単位律が、通常の（例えば整数の掛け算の）結合律・単位律とほんとに同類であることを納得するには、相当に抽象的な定式化が必要です。

「圏、関手、モナドはどうしたら分かるの？」の最後で：

モナド（monad）とモノイド（monoid）の発音が似ている（紛らわしい！）のは偶然なのでしょうか？僕は事情を知りません。が、実際のところ深い関係があるのは確かです。...(省略)
... これ以上詳しい説明はやめますが、下の表に、いろいろな圏におけるモノイド概念を挙げます。

と、結局いいかげんにお茶を濁しているな。今日はもう少し先へ進むぞ。

循環的な状況が恐いけど魅力的

「モナドはモノイドだ」と語ろうとすると僕は、なんかこう背筋がゾワゾワするんですよ。

普通の（集合ベースの）モノイドという概念がある。
モノイド概念を一般化できる。
一般化のためにはモノイド圏を使う。
モノイド圏は、一般化されたモノイド概念である。

一般化モノイドの定式化に一般化モノイドの特殊例が必要。ウヒャーッ、循環してるよー。形式的には矛盾は出ないのだけど、気分としてはなんか恐い。次のエントリーでも「モノイド恐い」と叫んでいます。

恐いけど心惹かれる、ゾワゾワ。

準備：ボックス図からストリング図へ

集合A, Bの直積をA×Bとして、写像f:A×B→Cを考えます。fを図示するのにいくつかの流儀があります。

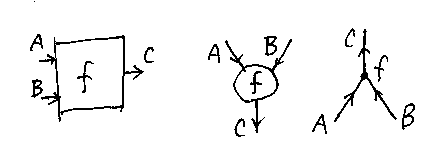
左の図は、fを箱で描いているのでボックス図と呼びます。ほんとはボックス＆ワイヤー図なんだけど、主役は箱でワイヤーは箱から出る端子（コネクタ、ピン）を示すだけ。

まんなかの図は、「バエズとステイのロゼッタストーン論文と現代のヒエログリフ」で紹介した論文で使われています。箱の代わりに丸、方向は左から右じゃなくて上から下です。

物理では、上から下より下から上に描くほうが多数派です。右の絵は、下から上の方向で描いています。そして、fを表す丸は点に退化してます。これはもう、物理のファインマン図ですね。

今回使う図式法は、ロゼッタストーン論文の図とファインマン図の中間的なもので：

方向は常に上から下、矢印は省略してよい。
fは小さな丸で描き、文字fは丸のなかに書く。
A, B, Cは線で描き、文字A, B, Cは線のラベルとして書く。

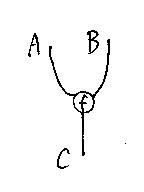
この図式法だと、“線＝紐”が主役なのでストリング図と呼びます*1。集合と写像だけじゃなくて、A, B, Cは圏の対象、fは射、×はモノイド積（後述）の状況でストリング図を使います。

準備：徹底的に左から右の記法

関手と自然変換の計算では、何を計算しているか分からなくなるので、使う文字で種類を区別しておきましょう。

圏：C, D, Eなど（イタリック）
圏の対象：A, B, Cなど
圏の射：f, g, hなど
関手：F, G, Hなど
自然変換：α、β、γなど（ギリシャ文字）

射の結合（合成）は「;」を使って図式順（diagrammatic order）でf;gと書きます。関手の結合F;Gも同様。射と関手には矢印「→」を使いますが、自然変換は「⇒」にします。

f:A→B は射
F:C→D は関手
α::F⇒G は自然変換（コロンを2つにする）

結合を図式順で書いても、適用が反図式順だと、計算がスムーズに進みません。慣例とは違いますが、F(A)はA.Fと書きます。メソッド呼び出し person.getName() を関数記法で書くなら getName(person) ですが、これを逆向きに考えて、適用F(A)をA.Fと書くわけ。A.F.Gは(A.F).Gのことです。

自然変換αのA成分はα_Aと書くのが習慣ですが、これもA.αにします。例えば、G(F(α_A))は、((A.α).F).G) = (A.α).F.G = A.α.F.G です。β_F(A)なら、(A.F).β = A.F.β ですね。

この記法は、図式と相性がよく、テキストエディタでも書きやすく、短く書けます。図を横目で睨みながら手計算するときは、絶対に有利です。（「図式順テキスト記法（DOTN）」は、もっと徹底してイタリックや添字を一切使わない記法の提案。）

自己関手の圏End(C)

よく出てくるモノイド圏、例えばデカルト圏やコンパクト閉圏は対称性を持っています。また、結合律や単位律はup-to-isoでしか成立しない例が多いですね。ところが圏Cの自己関手（endo-functors）の圏End(C)は、対称ではなく、結合律や単位律はon-the-noseで成立するという、ちょっと変わった例です。

E = End(C)として、圏Eがどんな圏なのかを説明します。

Obj(E) = |E| は、F:C→C という関手の全体。
ホムセットE(F, G)は、α::F⇒G:C→C という自然変換の全体。
F∈|E|、つまり関手F:C→C に対するid_Fは自明な自然変換（後述）。
α∈E(F, G)とβ∈E(G, H)の結合はα;βは、自然変換の縦結合（後述）。

まず、ホムセットE(F, G)が集合になるかどうか気になります。僕はよく分かりません ^^; 集合になるケースだけを考えるか、気にしないかにしましょう。

さて、id_Fとα;βの定義は次のとおりです。ただし、id_Fは自然変換なので、ギリシャ文字ι＜イオタ＞を使って、ι_Fとします。

A.ι_F = id_A.F、id_A.F:A.F→A.F in C （[追記]ここ、間違っていたので直した。[追記]）
A.(α;β) = (A.α);(A.β)、A.α:A.F→A.G, A.β:A.G→A.H in C

確認すべきことは、ι_FがF⇒Fという自然変換であること、α::F⇒G、β::G⇒H に対してα;βがF⇒Hという自然変換であることです。さらに、次が必要です。

ι_F;α = α;ι_G = α （単位律）
(α;β);γ = α;(β;γ) （結合律）

これらのことは、可換図式を眺めながら計算すれば出ます（次節に計算に関するオシャベリ）。具体的な計算は、記法が少し違いますが「図式順テキスト記法（DOTN）」に書いてあります。

このエントリーの記法	図式順テキスト記法
C, D	C, D
A, B, C	a, b, c
F;G	F;;G
ι_F	F^
α;β	α\|β

余談：圏論は、ほぼ計算だけ

圏論は、抽象的な印象を受けます（事実、まー抽象論と言っていいでしょう）が、定義を理解したら（いや、理解できなくても）、あとは計算するだけです。僕はモノグサなので、計算の手間を嫌って他の手段で理解しようと試みたりしますが、結局我慢して計算するハメになります。教訓としては、四の五の言ってないで計算するほうがいいと思います。

計算のとき混乱するのを避けるため、僕は、恒等ナントカは次のように書き分けています。

恒等射 id_A: A→A
恒等関手 Id_C:C→C
恒等自然変換 ι_F::F⇒F:C→C （一般的には、F:C→D）

「図式順テキスト記法（DOTN）」では、結合さえも書き分けています。

射の結合 f;g
関手の結合 F;;G
自然変換の結合 α|β

今回このエントリーでは、記号「;」をオーバーロードして、結合はなんであれ「;」にしてみました。結合されるモノが、英小文字、英大文字、ギリシャ小文字で書き分けられているので混乱は少ないだろうと判断してです。（でも、A.(α;β)が(A.α);(B.β)はちょっと気持ち悪い、A.(α|β) = (A.α);(A.β) のほうがいい感じ。）

経験上、計算をしないと進まないのは知っているのですが、それでも計算は苦痛なので、絵でできることは絵で済ませるようにしています。罫線のあるノートに記号を並べるよりは、白紙のスケッチブックに絵を描くほうが楽しい気分がするんです。もっとも、絵に頼り切っているので、等式計算がますます出来なくなっちゃいましたけど(苦笑)。

厳密モノイド圏

我々の目的は、圏C上の自己関手の圏E = End(C)が、モノイド圏であることを示して、「モナドはモノイドだ」という主張を明らかにすることです。

まずはモノイド圏の定義ですが、ここでは厳密モノイド圏（strict monoidal category）について述べます。End(C)は厳密モノイド圏だし、一般の（厳密ではない）モノイド圏だと扱いがだいぶ難しくなるので。

(C, □, I)が厳密モノイド圏であるとは：

Cは、圏である。
□は、C×C→C という双関手（bifunctor; 二項関手）である。
Iは、Cの特定された対象である。
□とIが、単位律と結合律を満たす。

□が双関手であるとは、単に直積圏C×C上の関手であることです。C×Cに属するペアを<f, f'>などと書くことにして、関手性を露骨に書き下すと、

□(<f, f'>;<g, g'>) = □(<f, f'>);□(<g, g'>)
□(id_{<A, A'>}) = id_{□(<A, A'>)}

□(<f, f'>)をf□f'のように、□を中置演算子記法で書くとずっとわかりやすくて、

(f;g)□(f';g') = (f□f');(g□g') （定義 <f, f'>;<g, g'> = <f;g, f';g'> を使う）
id_A□id_A' = id_A□A' （定義 id_{<A, A'>} = <id_A, id_A'> を使う）

特に (f;g)□(f';g') = (f□f');(g□g') は、交替律（interchange law）と呼ばれます（交替律については「指を使った足し算と interchange law」も参照）。（[追記]id_A□id_A' = id_A□A'のほうも交替律と呼ぶこともあるようです。[/追記]）

単位律と結合律は、（中置演算子記法で書くなら）お馴染みのものです。

I□A = A□I = A
(A□B)□C = A□(B□C)
id_I□f = f□id_I = f
(f□g)□h = f□(g□h)

二項演算□をモノイド積、特別な対象Iをモノイド単位と呼びます。

実例：行列の圏

集合圏に直積、または直和を考えるとモノイド圏です。ベクトル空間の圏とテンソル積を一緒に考えてもモノイド圏です。しかし、これらのモノイド圏は厳密モノイド圏ではなく、まじめに取り扱うとup-to-isoの議論が必要です。

「はじめての圏論その第2歩：行列の圏」で述べた行列の圏Matは、厳密モノイド圏になります。そのモノイド積を(+)（プラスを丸で囲んだ記号）で表すとして、

対象のモノイド積は整数の足し算 n(+)m = n + m
射のモノイド積は行列の対角ブロック和

行列の対角ブロック和は、次の例を見ればわかるでしょう。

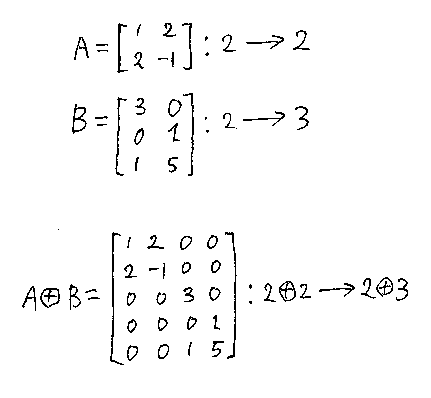
モノイド単位は整数0です。

(+)の関手性と単位律／結合律を、行列圏の記法にあわせて書き下せば：

(A;B)(+)(A';B') = (A(+)A');(B(+)B')
I_A(+)I_A' = I_A(+)A'

0(+)n = n(+)0 = n
(n(+)m)(+)k = n(+)(m(+)k)
I₀(+)A = A(+)I₀ = A
(A(+)B)(+)C = A(+)(B(+)C)

I₀ = []:0→0 は空（0行0列）な行列です。はいっ、後は計算して確認するだけ。

実例：非負の実数

非負の実数（non negative reals）から、NNRという厳密モノイド圏を作ってみましょう。圏NNRの対象類は、非負実数の全体です：Obj(NNR) = {x∈R | x ≧ 0}。x ≦ yのとき、そのときに限って射x→yがあるとします。この射を[x, y]と書きます。[x, y]は、実数直線上の区間と思ってもいいでしょう。

ホムセット：x≦yなら NNR(x, y) = {[x, y]}, そうでないなら NNR(x, y) = {}
dom, cod：dom([x, y]) = x, cod([x, y]) = y
結合： [x, y];[y, z] = [x, z]
恒等: id_x = [x, x]

NNRに、モノイド積は足し算、モノイド単位は0とすれば厳密モノイド圏になります。

対象のモノイド積は x+y
射のモノイド積は [x, y]+[x', y'] = [x+x', y+y']

[追記]非負であることは本質的ではなくて、実数全体としてもかまいません。正実数（0は除く）を考えて、掛け算x*yをモノイド積、1をモノイド単位としても、足し算のときと同様に厳密モノイド圏になります。より一般に、プレ順序を備えたモノイドは、やせた厳密モノイド圏となります。[/追記]

実例：釘にラベルが付いたブレイド図の圏

アミダ図やブレイド図の圏では、行列の圏と同様に、対象のモノイド積は整数の足し算、射のモノイド積は図を並置することとして厳密モノイド圏になります*2。

アミダ図やブレイド図の圏の対象を、単なる整数ではなくて記号列にすることができます。すると、対象のモノイド積は記号列の連接演算になります。

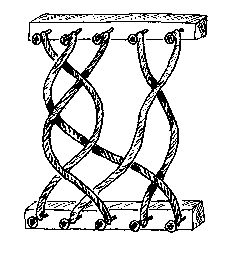
上図のごとき本物のブレイド（組み紐）で、釘（ペグ）の頭に何か記号が割り振ってあるとします。例えば、{a, b, c}のどれかの文字が各釘に刻んであるとしましょう。上の横木は a,a,c,b,a、下の横木は b,c,b,c,b と釘が並んでいるとき、ブレイドは a,a,c,b,a → b,c,b,c,b（もっと簡単に aacba→bcbcb）という射だと考えます。

すると、ブレイドを描いたブレイド図のdom, codは、記号{a, b, c}から作られる記号列となります。記号列の連接とブレイド図の並置がモノイド積を与え、空列（しばしばεと書かれる）がモノイド単位です。